Bayes’ Theorem
예제 1
특정 부부에게서 여아가 태어날 확률
| | 특정부부에게서 여아가 태어날 확률 |
|---|---|
| 여아가 더 많은 경우 | P1 = 0.6 |
| 비슷 | P2 = 0.5 |
| 남아가 더 많은 경우 | P3 = 0.4 |
-
class : 각 case의 확률이 class
- P(P=0.6) : 0.6의 확률로 여아를 낳을 확률을 가진 class
- P(P=0.5) : 0.5의 확률로 여아를 낳을 확률을 가진 class
- P(P=0.4) : 0.4의 확률로 여아를 낳을 확률을 가진 class
-
현상 : 어떤 부부에게서 아이가 태어났는데 여아가 태어난 상황
-
prior probability = 1/3
- 사전 지식이 제공되지 않았기 때문에 동등한 확률
-
Likelihood(어떤 클래스에서 어떤 현상이 일어날 확률)
- class의 현상을 보는 것, 확률
P(G | p=0.6) = 0.6
P(B | p=0.6) = 0.4
P(G | p=0.5) = 0.5
P(B | p=0.5) = 0.5 / P(G | p=0.4) = 0.4
P(B | p=0.4) = 0.6
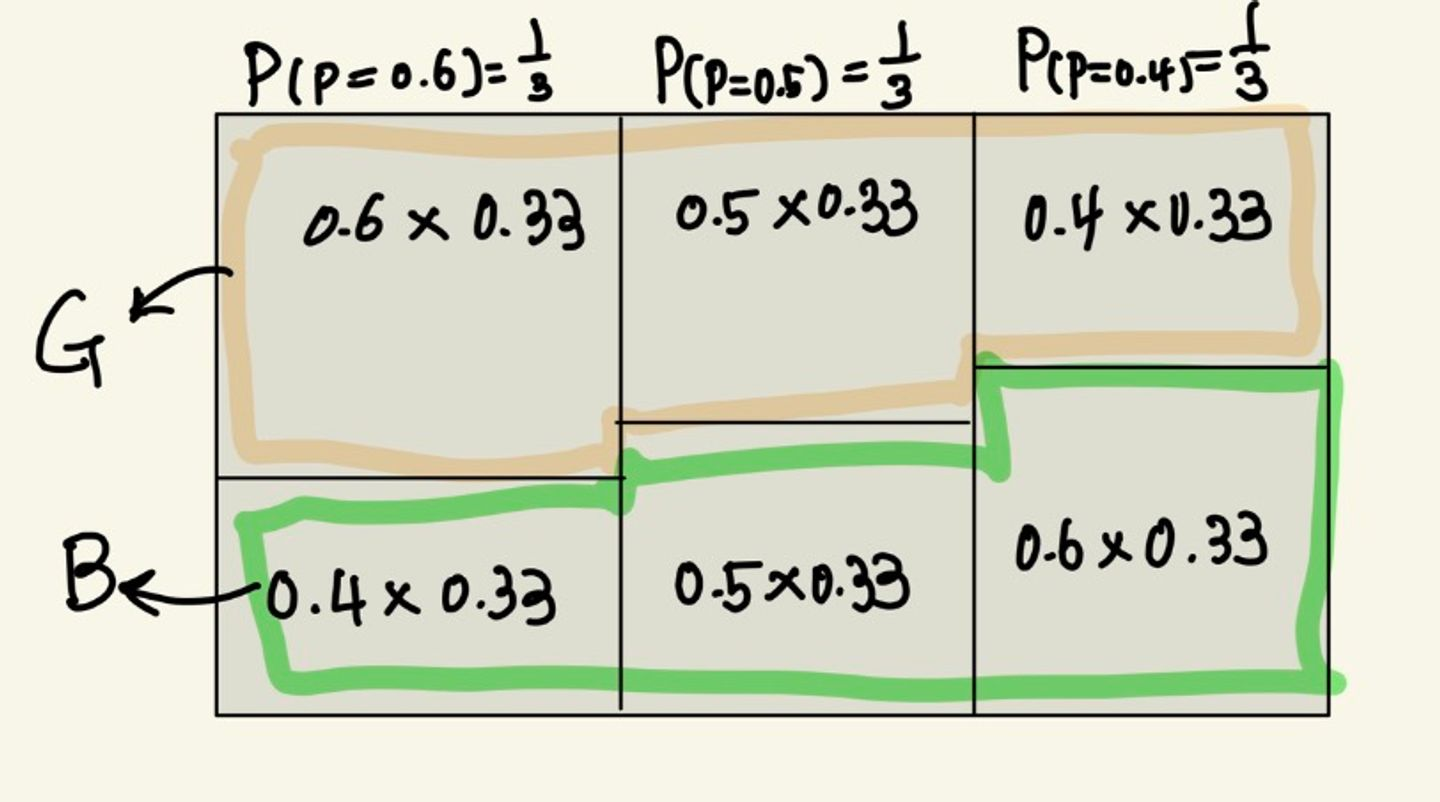
P(p=0.6 | G) = [P(G | p=0.6) * P(p=o.6)] / p(G) = [0.6*(1/3)]/0.5 = 0.4
P(p=0.5 | G) = [P(G | p=0.5) * P(p=o.5)] / p(G) = [0.5*(1/3)]/0.5 = 0.333
P(p=0.4 | G) = [P(G | p=0.4) * P(p=o.4)] / p(G) = [0.4*(1/3)]/0.5 = 0.26
P(p=0.6 | B) = [P(B | p=0.6) * P(p=o.6)] / p(B) = [0.6*(1/3)]/0.5 = 0.26
P(p=0.5 | B) = [P(B | p=0.5) * P(p=o.5)] / p(B) = [0.5*(1/3)]/0.5 = 0.333
P(p=0.4 | B) = [P(B | p=0.4) * P(p=o.4)] / p(G) = [0.4*(1/3)]/0.5 = 0.4
예제 2
Link → Spam : 0.6 (스팸메일인데 링크가 있을 확률)
Link → Ham : 0.2 (스팸메일이 아닌데 링크가 있을 확률)
Word → Spam : 0.4 (스팸메일인데 단어가 있을 확률)
Word → Ham : 0.05 (스팸메일이 아닌데 단어가 있을 확률)
<#1. Link>
class : Spam , Ham
prior probaility : P(S) = 0.5, P(H) = 0.5
Likelihood : P(L | S) = 0.6, P(¬L | S) = 0.4, P(L | H) = 0.2, P(¬L | H) = 0.8
**Posterior probability**
P(S | L) = [P(L | S)*P(S)]/p(L) = [(1/2)*0.6]/(1/2)(0.6+0.2) = 0.75
<#2. Word>
class : Spam , Ham
prior probaility : P(S) = 0.5, P(H) = 0.5
Likelihood : P(W | S) = 0.4, P(¬W | S) = 0.6, P(W | H) = 0.05, P(¬W | H) = 0.95

**Posterior probability**
P(S | W) = [P(W | S)*P(S)]/p(W) = [(1/2)*0.4]/(1/2)(0.4+0.05) = 0.89
<#3. 클래스 기준 테이블 생성 >
위의 Likelihood를 이용하여 Table을 그려보면, 두 개의 Table을 그릴 수 있음
| | Spam | Ham |
|---|---|---|
| Link | 0.6 | 0.2 |
| Not Link | 0.4 | 0.8 |
| | Spam | Ham |
|---|---|---|
| Word | 0.4 | 0.05 |
| Not Word | 0.6 | 0.95 |
위의 Table을 기반으로 두 정보를 결합한 Likelihood Table을 그리면 아래와 같다.
[SPAM]
| | Word | Not Word |
|---|---|---|
| Link | 0.24 | 0.36 |
| Not Link | 0.16 | 0.24 |
[HAM]
| | Word | Not Word |
|---|---|---|
| Link | 0.01 | 0.19 |
| Not Link | 0.04 | 0.76 |
위의 두 정보를 그림으로 그려보면 아래와 같이 표현할 수 있음
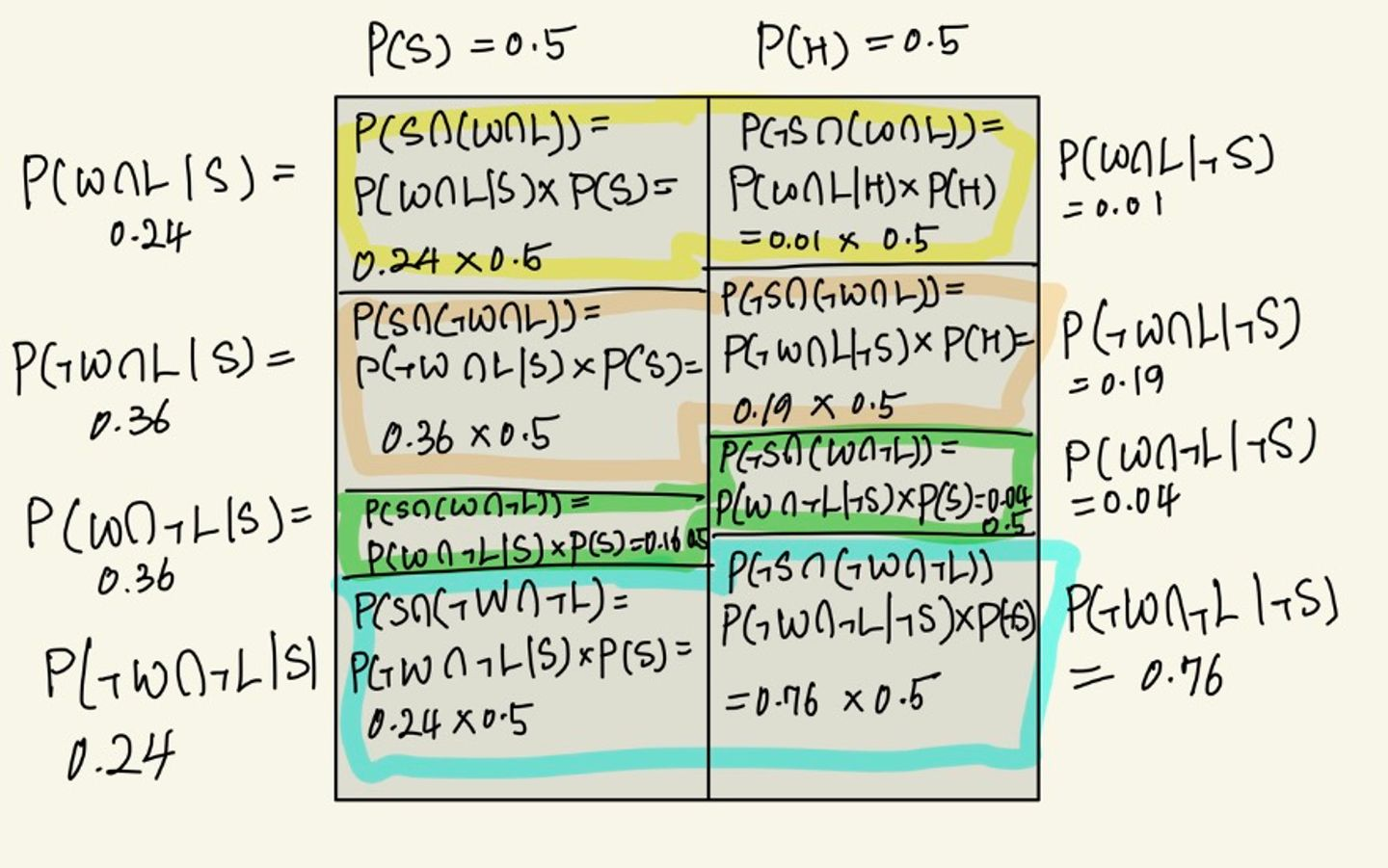
구하고자 하는 P(S | W∩L) = (0.24*0.5)/0.5(0.24+0.01) = 0.96
**재밌는 점**
word라는 정보 하나만 있을 때는 P(S | W) = 0.88
word, link 두 가지 정보를 모두 이용했을 때는 P(S | W∩L) = 0.96
베이즈 정리를 통해서 정보가 더 많을 때 클래스를 구분하는 것이 유용함을 알 수 있다. 넷플릭스가 유저에게 높은 정확도로 취향에 맞는 영상을 추천해준 이유 중 하나도 이 베이즈 정리를 통해 나온 결과다.
정보가 많아질 수록, 정확도가 올라간다.
