Classification:

• 예측하고자 하는 타겟값이 categorical한 경우

Binary classification

예시1) 이메일이 스팸인지 아닌지

예시2) 은행 소비자인지 아닌지

Multi-class Classification

여러 클래스 중 하나를 택하는

Regression:

• 연속적인 수에서 어떤 값을 예측하는 값을 예측하는 것

1. 집값을 예측
2. 시장 트렌드 예측
3. 유가 분석

Decision Tree

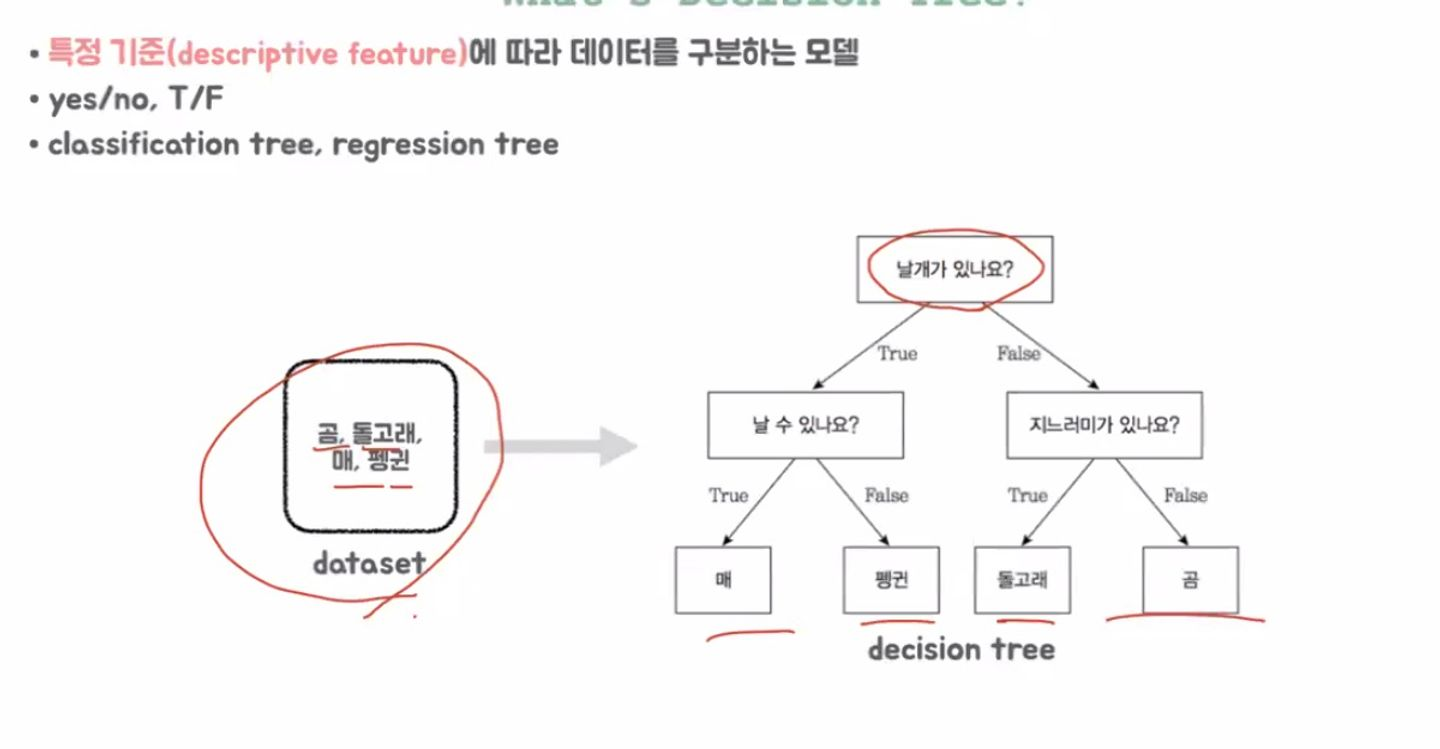
데이터가 주어졌을 때, 연속적인 질문에 따라 연속적 분기가 발생

• 특정 기준에 따라 데이터를 구분하는 모델
• Classification / Regression 두 가지 모두 사용할 수 있음
• yes/no | T/F 등으로 나눌 수 있음

예시의 경우 3번의 질문을 통해 결과값 분류

Nodes

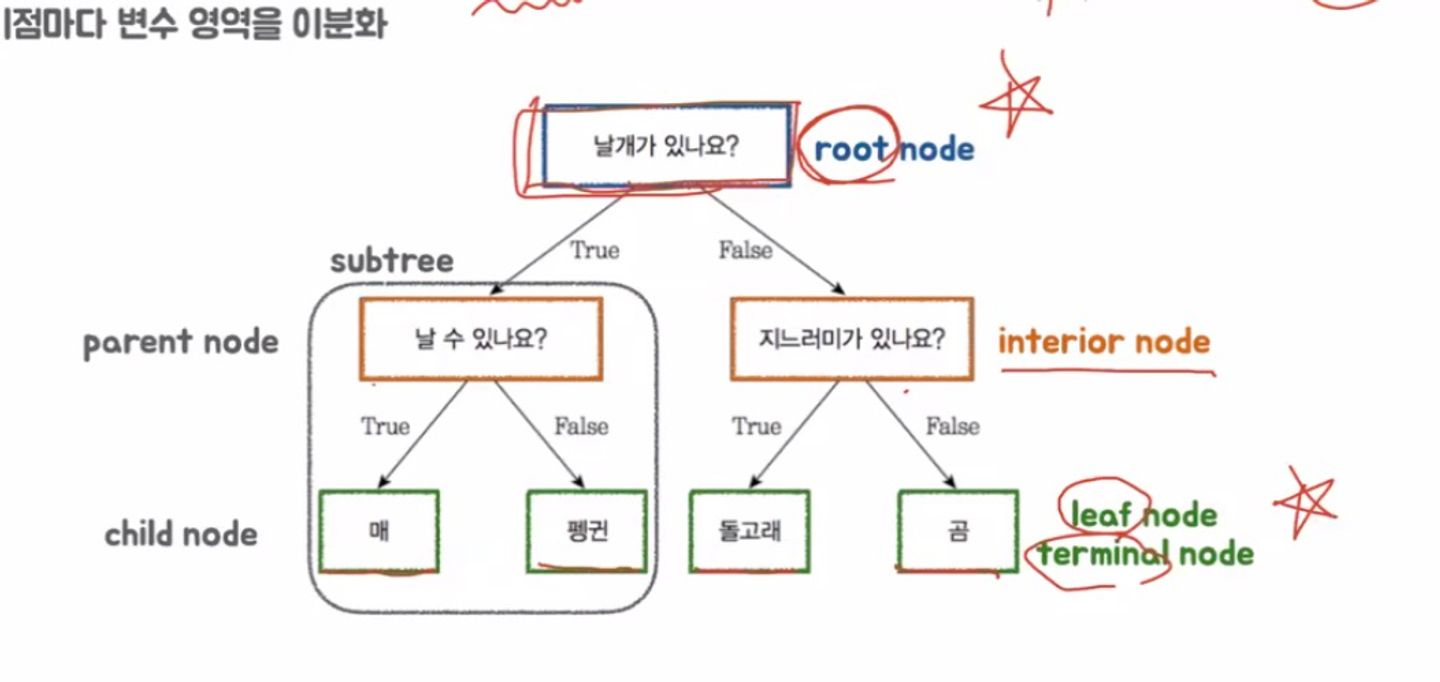
root node: 첫번째 분기

interior node: 가운데 분기

leaf node(=terminal node): 마지막 분기

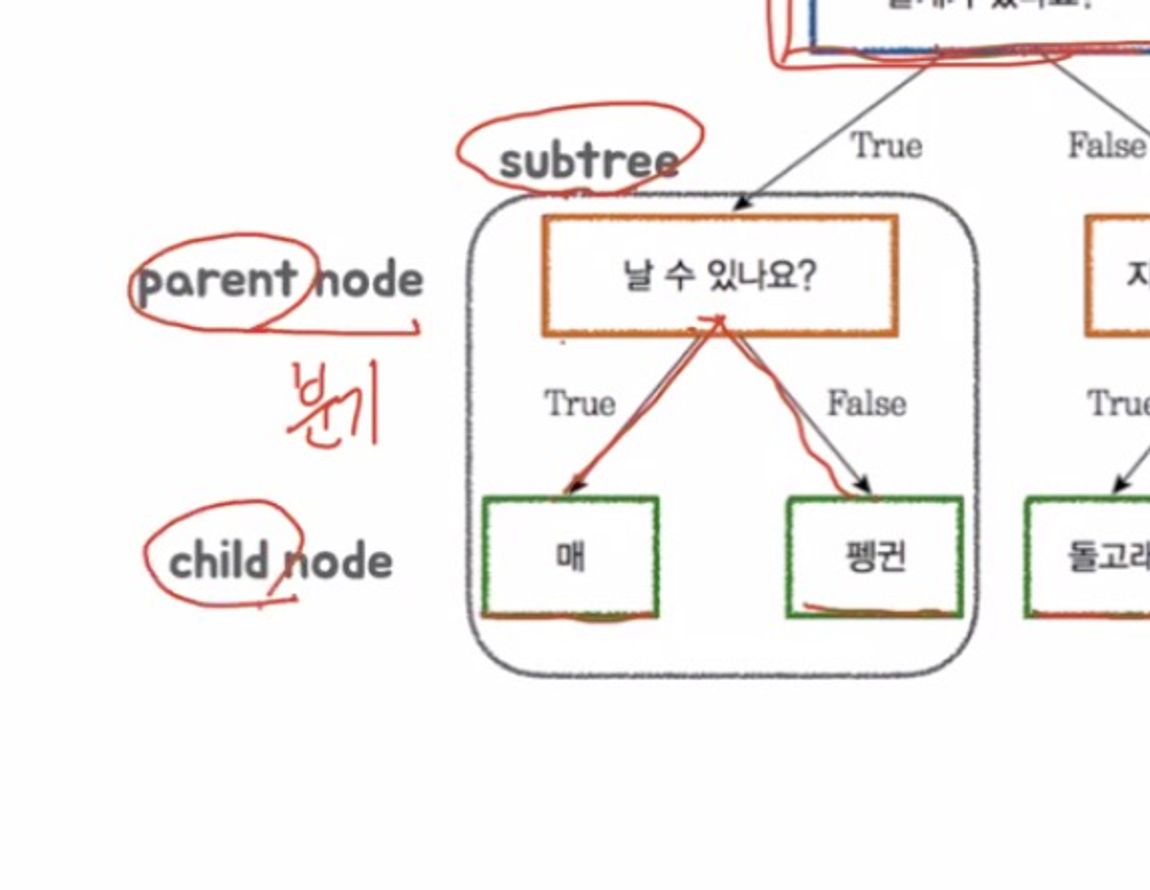
subtree: 트리 내부의 트리

parent node: subtree 상위 노드

child node: subtree 하위노드

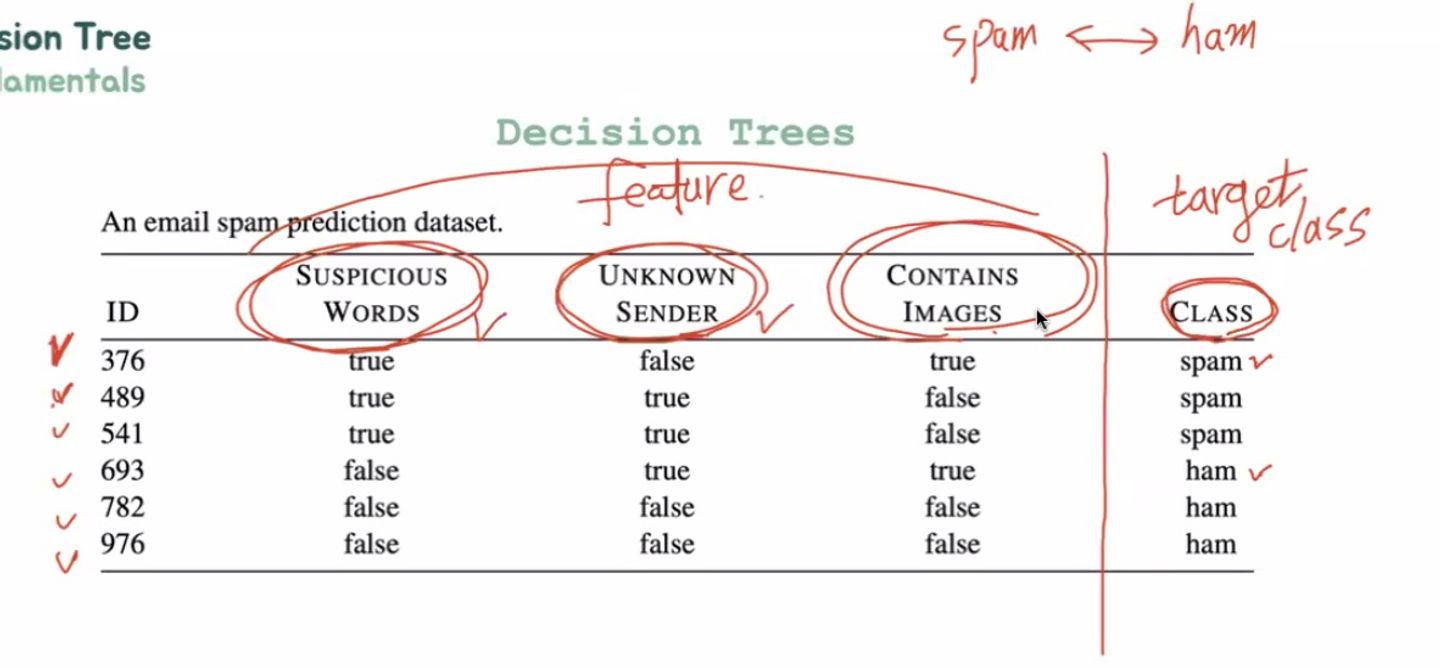
• 3가지 feature
• 하나의 target class

2. Entropy

Entropy?

무질서라는 뜻. 불순도를 측정하는 방법

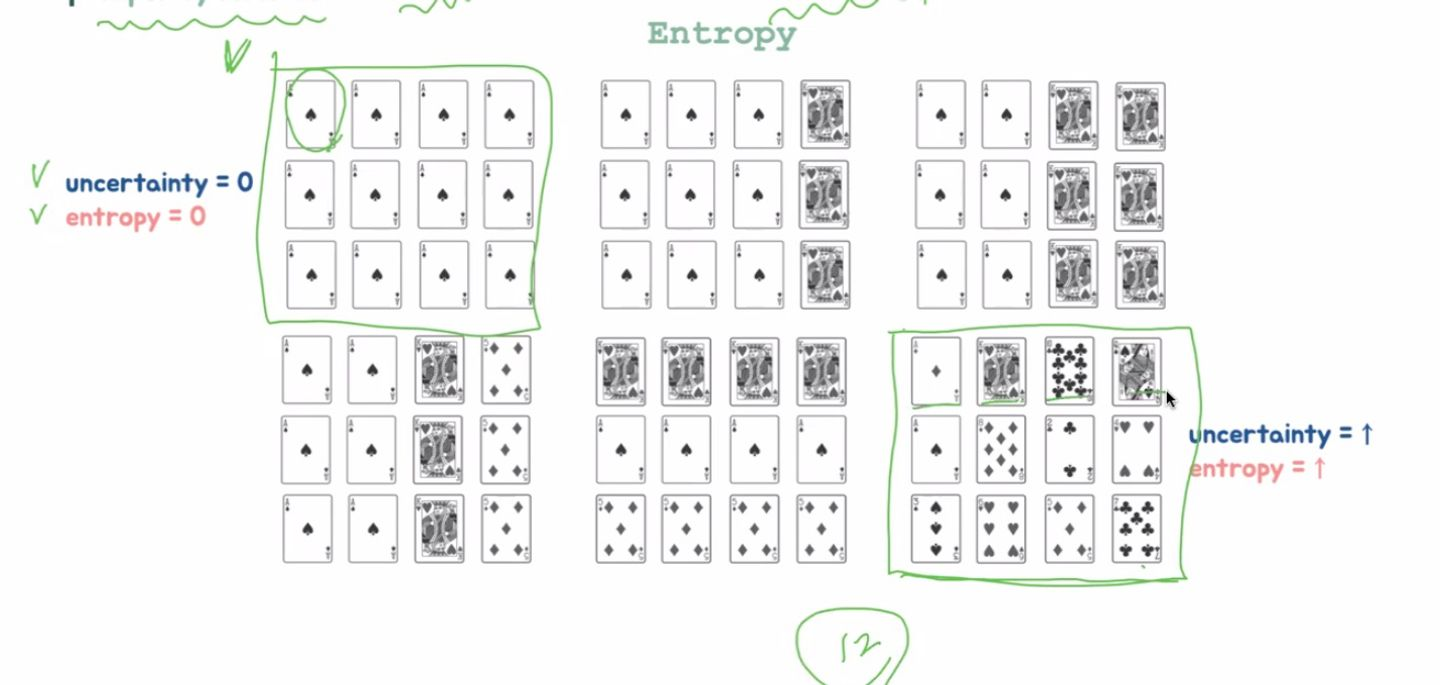
첫번째는 불순도, 즉 entropy가 0

마지막은 모두 다르기 때문에 entropy가 가장 높음

공식은 위와 같음.

Decision Tree = Information based M/L 이라고 한다. Decision Tree는 entropy가 낮아지는 곳으로 진행을 한다.

정보량(degree of surprisal, 놀람의 정도)

• 드물게 발생하는 사건일 수록 정보량이 크다
• 내일 대한민국에 지진이 발생한다 하면 극히 드문 발생이기 때문에 더 가치있는 정보다

• 엔트로피는 정보량의 기댓값(평균)
• 발생 사건들의 정보량 모두 구해서 (가중)평균
• 엔트로피 공식이 정보량에서 온 것.

Weighted Entropy

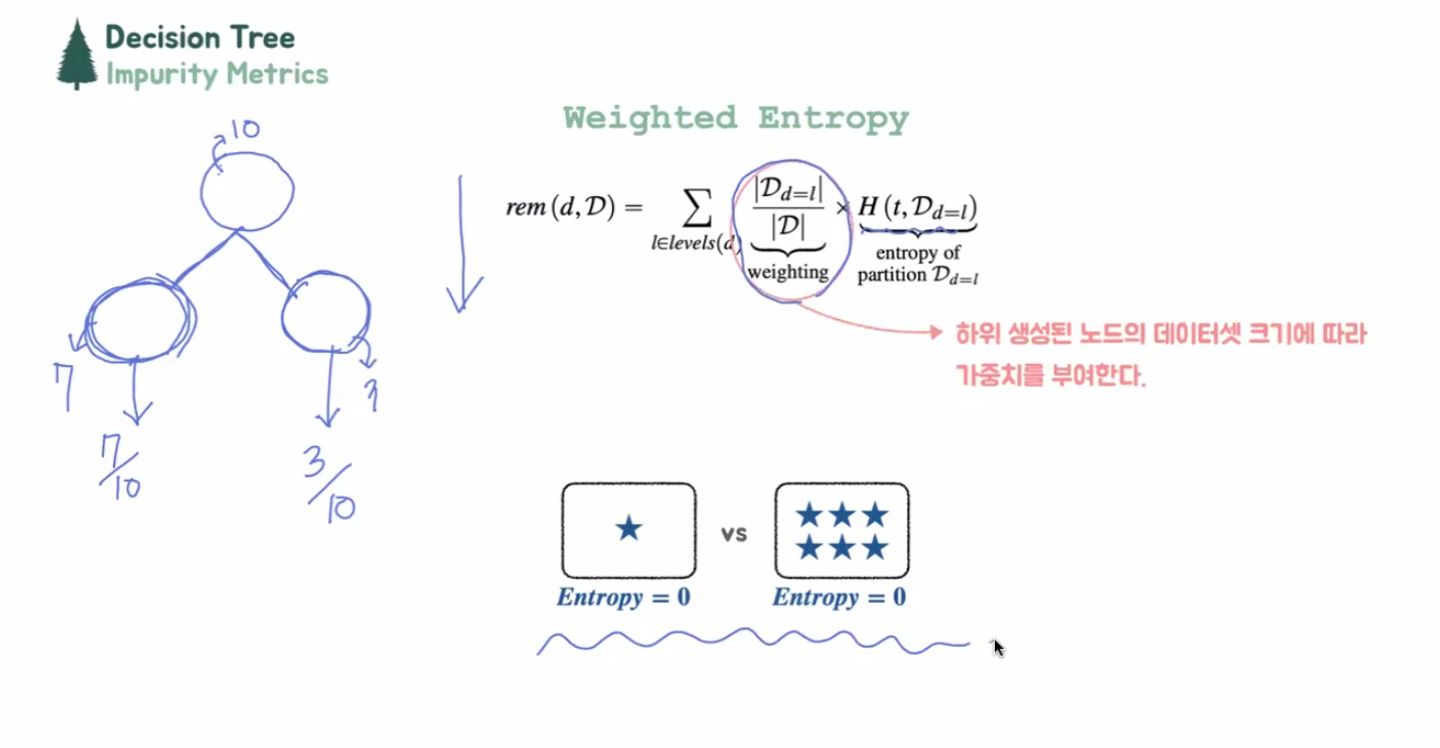
더 큰 덩어리에 더 큰 중요도를 부여해준다는 의미가 weighted Entropy

가중치, 즉 weight에 따라 노드의 데이터

Information Gain

분기 이전의 불순도와 분기 이후의 불순도의 차이(중요)

• 불순도를 측정하는 많은 방식이 있음 엔트로피 / 지니인덱스 등등,,

엔트로피는 불순도를 측정하는 기준이다. 라는 걸 기억하자.

**I · G**: H(분기 이전) - H’(분기 이후)

엔트로피: 불순도 / 인포메이션 게인: 분기 이전과 이후의 불순도 차이

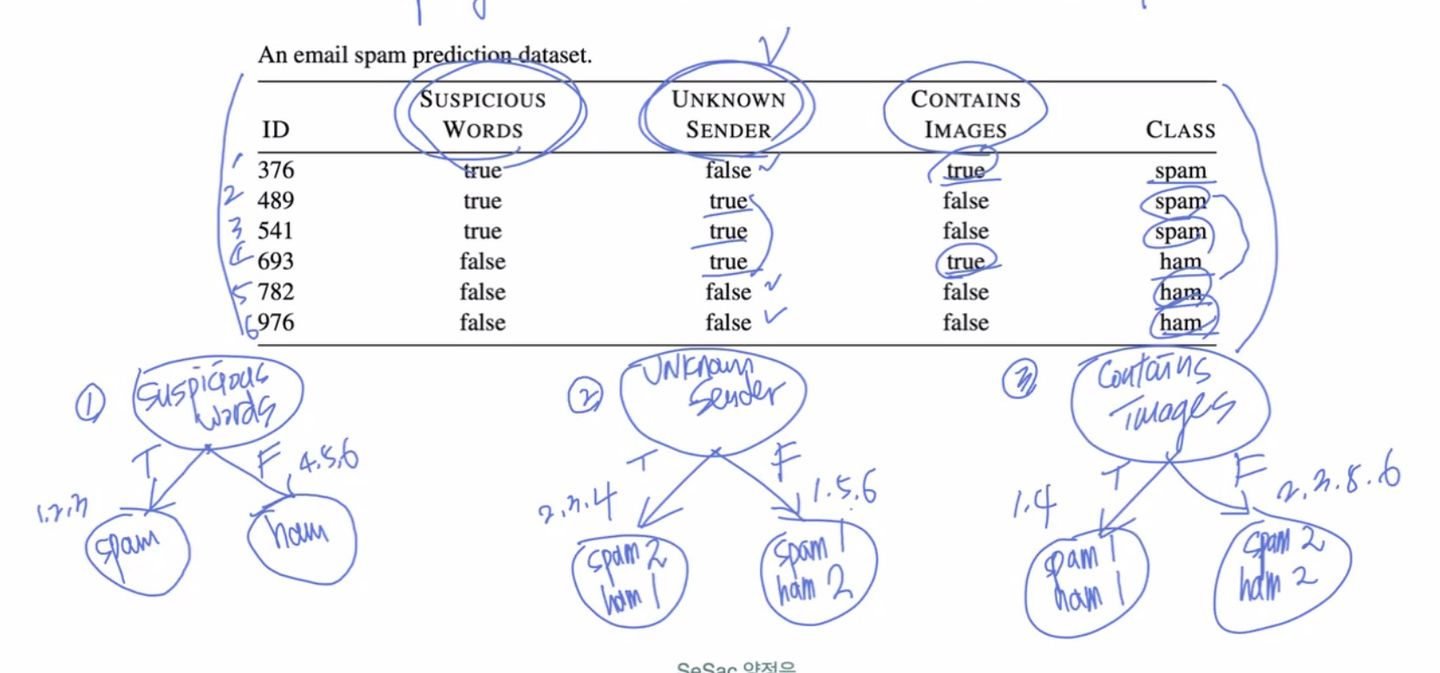
가장 효율적인 feature을 설정

• 분기 이전: 21/2log2(2) =1
• 엔트로피 기준은 항상 class

Information Gain: 분기 이전과 이후의 불순도 차이