Classification Decision Tree(continuous descripitve features)

이전 시간을 통해 Categorical Decision Tree를 만들어보는 연습을 해보았다. 그렇다면 연속적인 변수를 기준으로 feature를 설정해 Classification Decision Tree를 만들 순 없을까?

아래의 순서를 통해 그 활용을 해볼 수 있다.

Continuous Descriptive의 IG 구하는 방법

1. sorting values
2. target level이 다른 인접한 쌍 검색
3. 그 사이의 평균 값을 선택 가능한 threshold로 추정
4. 각 threshold를 분기점으로 설정했을 때 각각의 case에 대한 IG계산 후 가장 높은 값을 선택

ID	Stream	Slope	Elevation	Vegetation
1	false	steep	3,900	chapparal
2	True	moderate	300	riparian
3	True	steep	1,500	riparian
4	false	steep	1,200	chapparal
5	false	flat	4,450	conifer
6	True	steep	5,000	conifer
7	True	steep	3,000	chapparal

1. sorting values → 오름차순 정렬

• continuous feature인 elevation을 오름차순으로 정렬하면 아래와 같아진다.

ID	Stream	Slope	Elevation	Vegetation
2	True	moderate	300	riparian
4	false	steep	1,200	chapparal
3	True	steep	1,500	riparian
7	True	steep	3,000	chapparal
1	false	steep	3,900	chapparal
5	false	flat	4,450	conifer
6	True	steep	5,000	conifer

2. target level이 다른 인접한 쌍 검색

target level이 변하는 구간 파악하려면 어떻게 해야할까? feature인 Elevation을 기준으로 target class의 level이 나뉘는 기점을 살펴보면 된다. 위의 표를 기준으로 보자.

• 2번→4번일 때 target class가 변경(rip→cha)
• 4번→3번일 때 target class가 변경(cha→rip)
• 3번→7번일 때 target class가 변경(rip→cha)
• 1번→5번일 때 target class가 변경(cha→con)

이를 통해 총 4개의 threshold가 생긴다는 걸 알 수 있다

3. 그 사이의 평균 값을 선택 가능한 threshold로 추정

• 1st threshold(2번→4번) : (300+1200)/2 = 750
• 2nd threshold(4번→3번) : (1200+1500)/2 = 1350
• 3rd threshold(3번→7번) : (1500+3000)/2 = 2250
• 4th threshold(1번→5번) : (3900+4450)/2 = 4175

4. 각 threshold를 분기점으로 설정했을 때 각각의 case에 대한 IG계산

• 총 6개 feature의 IG값을 계산한다고 생각하면 된다.
• (Elevation의 분화)threshold 1~4, stream, slope
• Continuous Descriptive features는 path에 동일한 feature를 여러번 사용할 수 있다.
  • 가령 Elevation가 나뉘어진 theshold를 1~4 구간 동안 반복할 수 있다는 의미.

Root node 연산을 통해 구하기

#1단계: root node 구하기 -> 각 feauture로 분기했을 때, IG를 구해보기

ev_H = -((3/7)*np.log2(3/7)+(2/7)*np.log2(2/7)+(2/7)*np.log2(2/7))
print(ev_H)
ev_750_H_ = -((6/7)*(1/2*np.log2(1/2)+1/6*np.log2(1/6)+2/3*np.log2(2/3)))
print(ev_750_H_)
ev_750_IG = ev_H - ev_750_H_
print("ev_750_IG: ", ev_750_IG)

ev_1350_H_ = -((2/7*2*1/2*np.log2(1/2))+((5/7)*((1/5*np.log2(1/5))+(2*2/5*np.log2(2/5)))))
print(ev_1350_H_)
ev_1350_IG = ev_H - ev_1350_H_
print("ev_1350_IG: ", ev_1350_IG)

ev_2250_H_ = -(3/7*(2/3*np.log2(2/3)+1/3*np.log2(1/3))+4/7*2*1/2*np.log2(1/2))
print(ev_2250_H_)
ev_2250_IG = ev_H - ev_2250_H_
print("ev_2250_IG: ", ev_2250_IG)

ev_4175_h = -5/7*((2/5*np.log2(2/5)+3/5*np.log2(3/5)))
print(ev_4175_h)
ev_4175_IG = ev_H - ev_4175_h
print("ev_4175_IG: ", ev_4175_IG)

stream_h = -(4/7*((1/2*np.log2(1/2))+(1/4*2*np.log2(1/4)))+3/7*(2/3*np.log2(2/3)+(1/3)*np.log2(1/3)))
print(stream_h)
stream_IG = ev_H - stream_h
print("stream_IG: ", stream_IG)

slope_h = -(5/7*(3/5*np.log2(3/5))+1/5*np.log2(1/5)+1/5*np.log2(1/5))
print(slope_h)
slope_IG = ev_H - slope_h
print("slope_IG: ", slope_IG)

0.4245406355191399
0.18385092540042125
0.5916727785823274
0.863120568566631
0.30595849286804166
0.31204307200807513

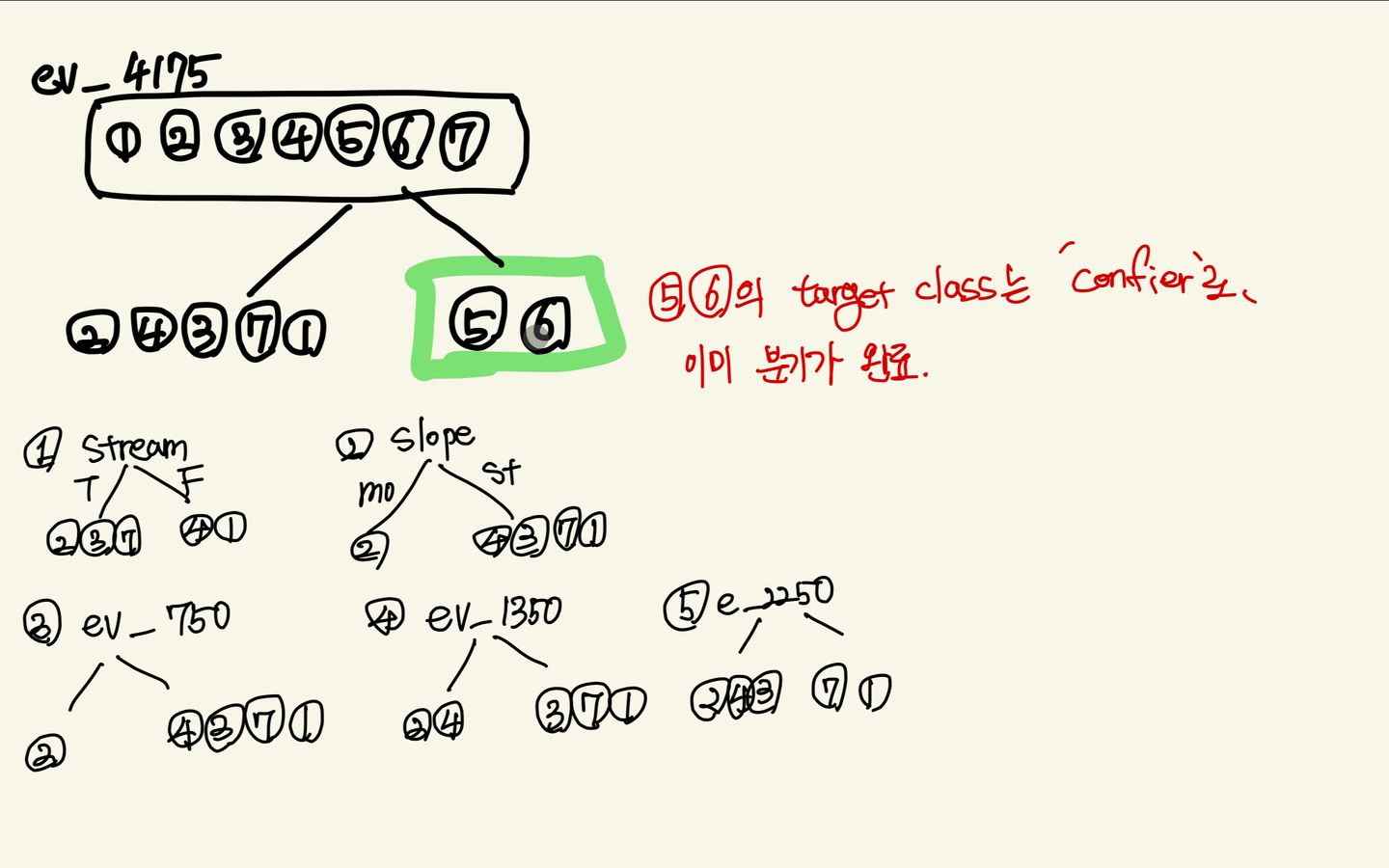
⇒root node에서 사용할 feature는 IG가 0.8631로 가장 높은 elevation_4715를 설정해준다. 그 다음 분기의 IG를 다시 계산해보자.

H = -((3/5*np.log2(3/5))+(2/5*np.log2(2/5)))
print(H)
ev_750_h = -(4/5*(3/4*np.log2(3/4)+1/4*np.log2(1/4)))
print(ev_750_h)
ev_750_IG = H - ev_750_h
print("ev_750_IG: ", ev_750_IG)

ev_1350_h = -((2/5*2*1/2*np.log2(1/2))+(3/5*(1/3*np.log2(1/3)+2/3*np.log2(2/3))))
print(ev_1350_h)
ev_1350_IG = H - ev_1350_h
print("ev_1350_IG: ", ev_1350_IG)

ev_2250_h = -(3/5*(2/3*np.log2(2/3)+1/3*np.log2(1/3)))
ev_2250_IG = H - ev_2250_h
print("ev_2250_IG: ", ev_2250_IG)

stream_h = -(3/5*(2/3*np.log2(2/3)+1/3*np.log2(1/3)))
stream_IG = H - stream_h
print(stream_h)
print("stream_IG: ", stream_IG)

slope_h = -(4/5*(3/4*np.log2(3/4)+1/4*np.log2(1/4)))
slope_IG = H - slope_h
print(slope_h)
print("slope_IG: ", slope_IG)

그런데 계산을 해보면 elevation 2250의 IG와 stream의 IG값이 동일하다

두 feature 각각 기준으로 그 다음 분기할 feature들을 계산해주자

case1: Stream

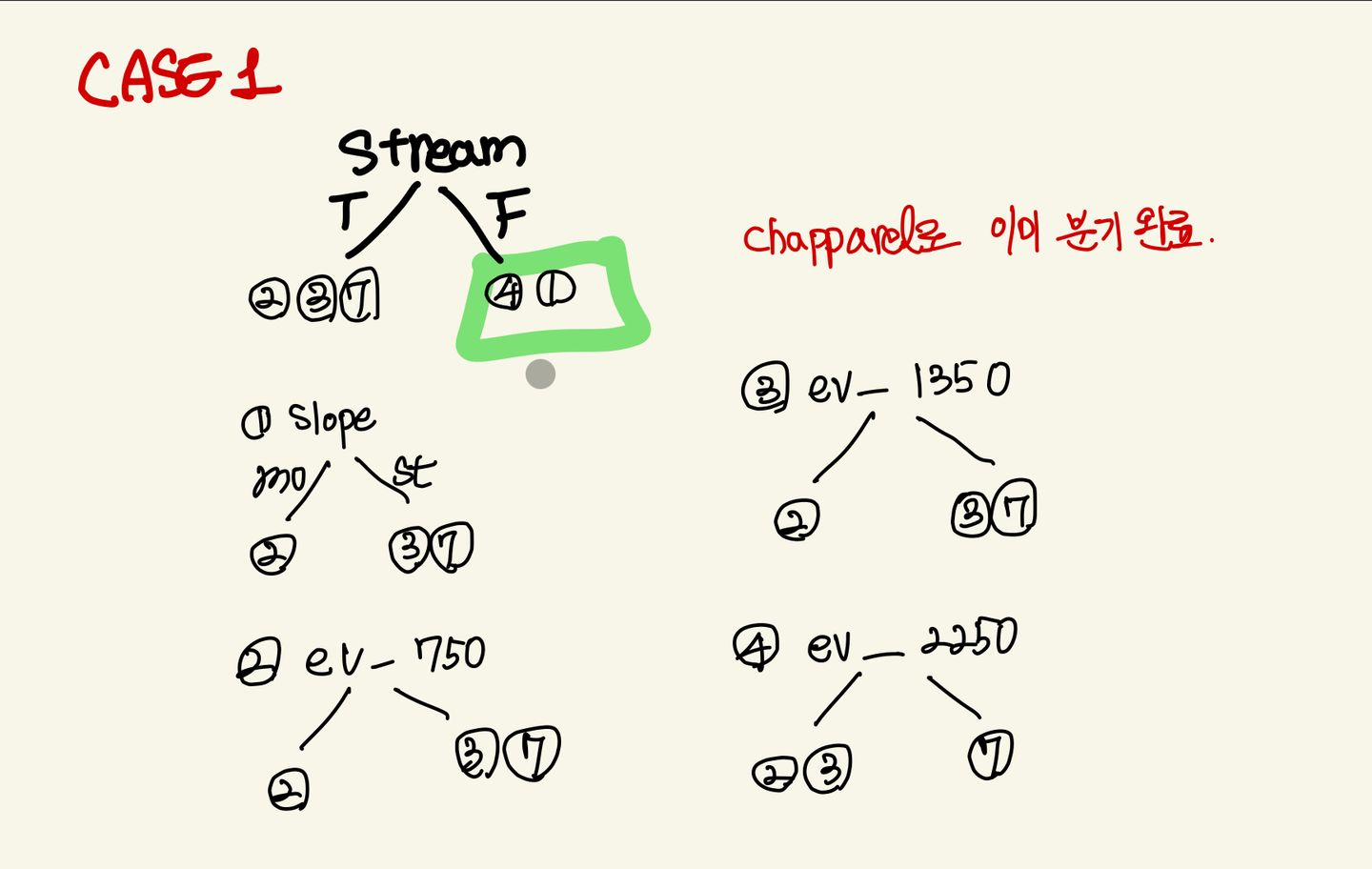
H = -(1/3*np.log2(1/3)+2/3*np.log2(2/3))
ev_750_h = -(2/3*2*1/2*np.log2(1/2))
ev_750_IG = H - ev_750_h
print("ev_750_IG: ", ev_750_IG)

ev_1350_h = ev_750_h
ev_1350_IG = H - ev_1350_h
print("ev_1350_IG: ", ev_1350_IG)

ev_2250_h = -(2/3*np.log2(1)+1/3*np.log2(1))
ev_2250_IG = H - ev_2250_h
print(H)
print("ev_2250_IG: ", ev_2250_IG)

slope_h = -(2/3*2*1/2*np.log2(1/2))
slope_IG = H - slope_h
print("slope_IG: ", slope_IG)

첫번째 케이스는 Stream이고, 시각화를 위처럼 된다.

case2: ev_2250

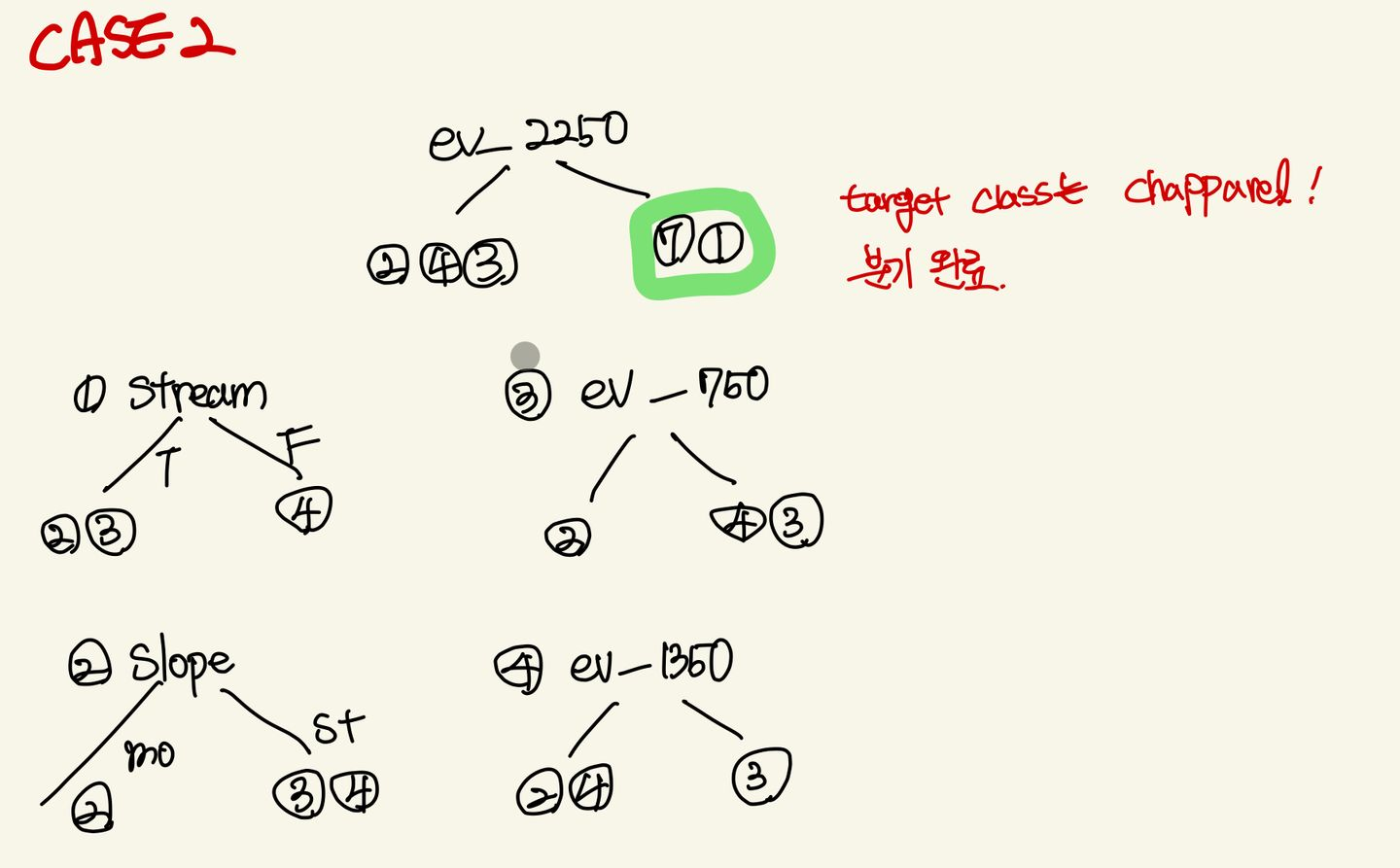
H = -(1/3*np.log2(1/3)+2/3*np.log2(2/3))
ev_750_h = -(2/3*2*1/2*np.log2(1/2))
ev_750_IG = H - ev_750_h
print(ev_750_h)
print("ev_750_IG: ", ev_750_IG)

ev_1350_h = -(2/3*2*1/2*np.log2(1/2))
ev_1350_IG = H - ev_1350_h
print(ev_1350_h)
print("ev_1350_IG: ", ev_1350_IG)

stream_h = -((2/3*np.log2(1))+(1/3*np.log2(1)))
stream_IG = H - stream_h
print(stream_h)
print("stream_IG: ", stream_IG)

slope_h = -(2/3*2*1/2*np.log2(1/2))
print(slope_h)
slope_IG = H - slope_h
print("slope_IG: ", slope_IG)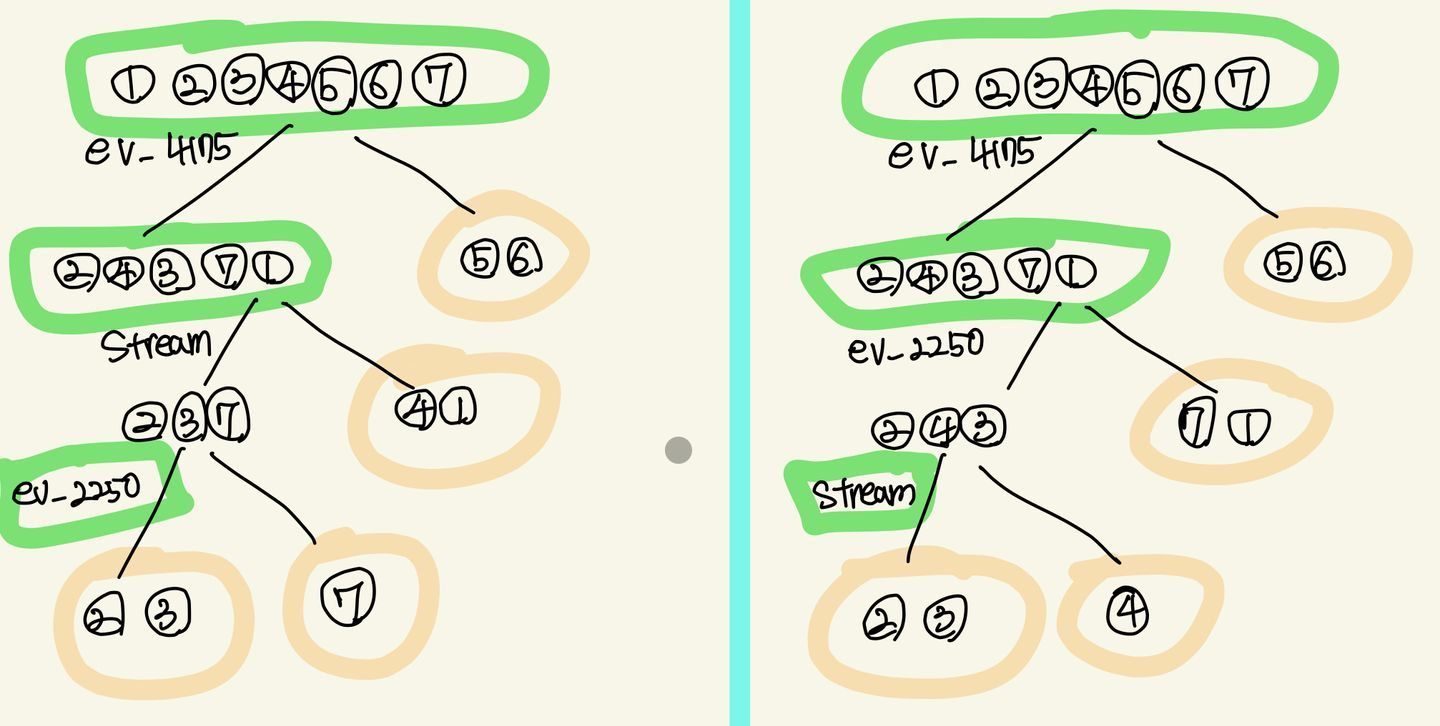

따라서 최종 결과물은 위와 같음! 분기 나뉜 것 좀 봐 이쁘다.

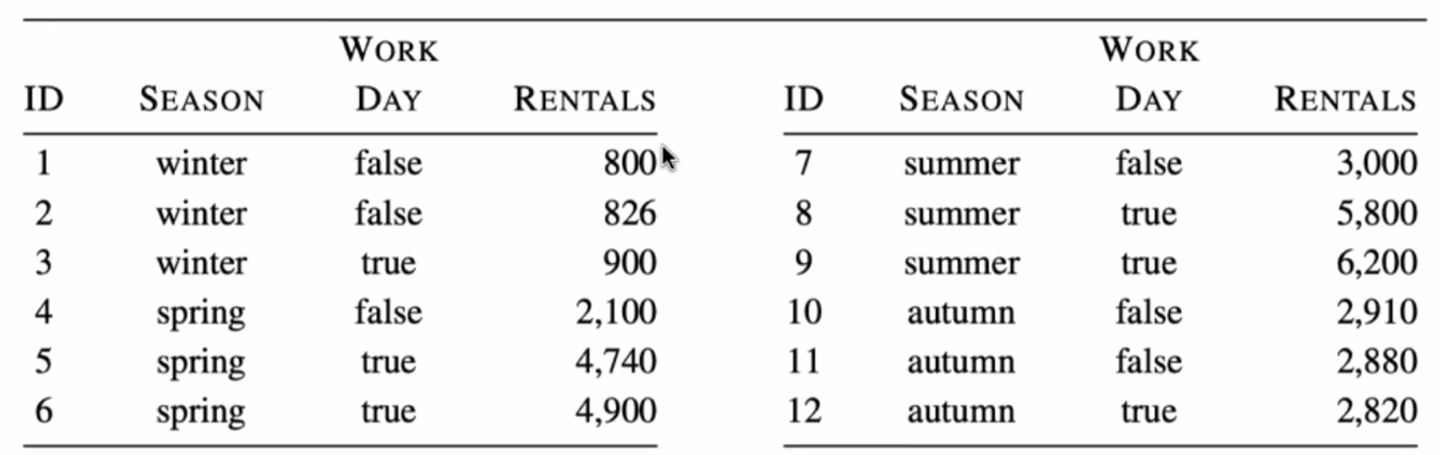
Continuous Target Features

target feature가 continuous한 경우는 Regression(회귀)다. 따라서 Regression Decision Tree를 그려야하며, Regression Decision Tree 에서는 분기 후 subset안에서 남은 값들의 평균이 leaf node의 대표값이 된다.

#️⃣dataset

#️⃣ Continuous target (연속형 숫자)인 경우 IG 구하는 방법

1. feature별로 분기를 한 후의 entropy를 구하는 대신 -> subset의 분산을 구함
2. 분산의 가중평균을 summation한 값이 최종 IG가 됨
3. IG가 가장 작은 경우(분산이 적게 된 경우)가 최적의 case로 간주하여 해당 feature를 해당 층의 분기용 node로 설정

❓왜 분모에 1이?

• 모집단의 평균은 표본 집단의 평균으로 대체 가능, 하지만 분산은 대체가 불가하다
• 자유도(df)를 고려해야 하기 때문

#️⃣ Regression Decision Tree(continuous target features인 경우)

• 특정한 값을 예측하는 것
• 어떤 feature로 나누었을 때 분산이 작아지는지 보는 것
• leaf node 안의 instance들의 mean
• 분산 = (편차)**2의 평균 / 편차: 평균과 각각의 데이터들 간의 차이
• 모집단의 평균은 표본집단의 평균으로 대체 가능하나, 모집단의 분산은 표본집단의 분산으로 대체할 수 없음. 표본집단의 분산은 모집단의 분산을 과소평가하기 때문에 (n-1)로 나누어줌
• 분기 이후의 분산값을 구할 때는 각각 가중치를 곱해야 함

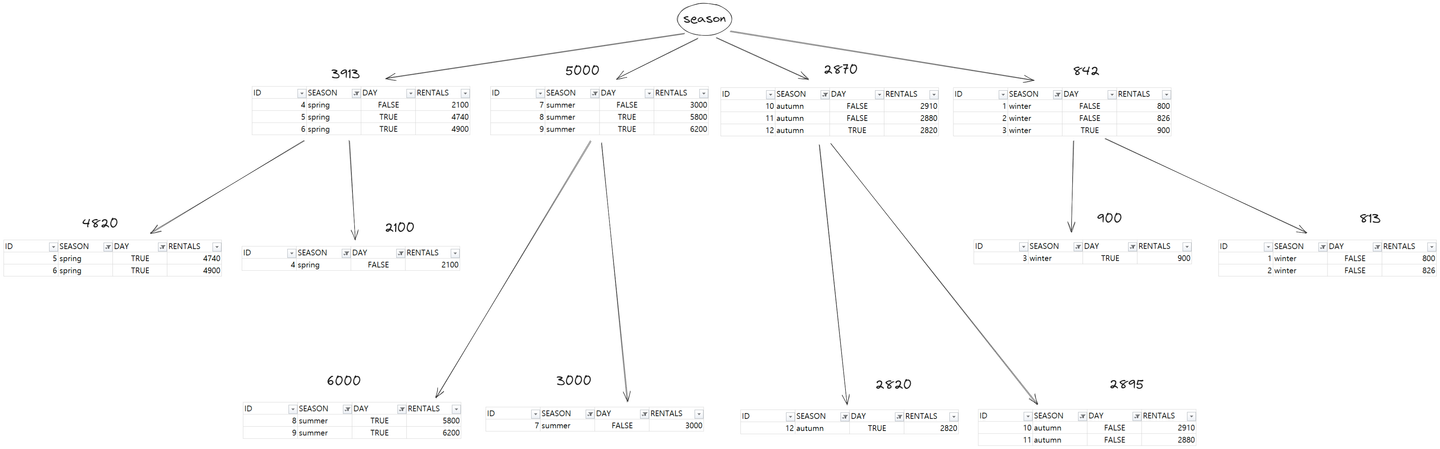
winter_mean = (800+826+900)/3
#print(winter_mean)
winter_var = (((winter_mean-800)**2)+((winter_mean-826)**2)+((winter_mean-900)**2))/(3-1)*1/4
print("winter_var: ", winter_var)

spring_mean = (2100+4740+4900)/3
#print(spring_mean)
spring_var = (((spring_mean-2100)**2)+((spring_mean-4740)**2)+((spring_mean-4900)**2))/(3-1)*1/4
print("spring_var: ", spring_var)

summer_mean = (3000+5800+6200)/3
summer_var = (((summer_mean-3000)**2)+((summer_mean-5800)**2)+((summer_mean-6200)**2))/(3-1)*1/4
print("summer_var: ", summer_var)

autumn_mean = (2910+2880+2820)/3
autumn_var = (((autumn_mean-2910)**2)+((autumn_mean-2880)**2)+((autumn_mean-2820)**2))/(3-1)*1/4
print("autumn_var: ", autumn_var)

season_var = winter_var + spring_var + summer_var + autumn_var
print("season_var: ", season_var)

true_mean = (900+4740+4900+5800+6200+2820)/6
true_var = (((true_mean-900)**2)+((true_mean-4740)**2)+((true_mean-4900)**2)+((true_mean-5800)**2)+((true_mean-6200))**2+((true_mean-2820)**2))/(6-1)*1/2
print("true_var: ", true_var)

false_mean = (800+826+2100+3000+2910+2880)/6
false_var = (((false_mean-800)**2)+((false_mean-826)**2)+((false_mean-2100)**2)+((false_mean-3000)**2)+((false_mean-2910)**2)+((false_mean-2880)**2)/(6-1))*1/2
print("false_var: ", false_var)

day_var = true_var + false_var
print(day_var)

• season의 variance < workday의 variance 이므로, season을 root node로 선택하여 분기하면 됨
• 분산값이 더 작은 leap node 값들의 평균이 해당 node를 대표하는 값

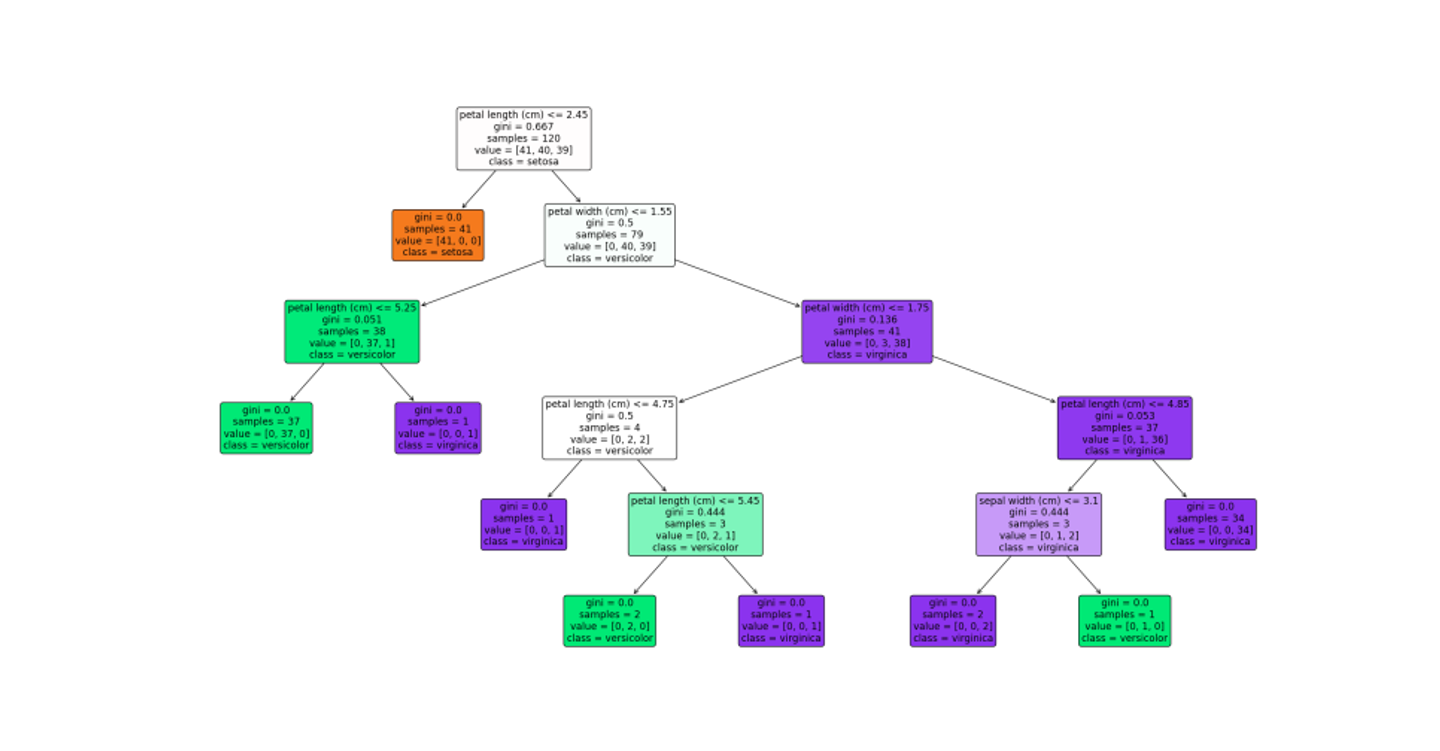
#️⃣sklearn을 이용하여 iris data의 decision tree 그려보기

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

iris = load_iris()
data, targets = iris.data, iris.target
print("data / target shape")
print(data.shape, targets.shape, '\n')

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target,
                                                    test_size=0.2, random_state=11)

# print(f"{type(X_train) = } / {X_train.shape = }")
# print(f"{type(X_test) = } / {X_test.shape = }")
# print(f"{type(y_train) = } / {y_train.shape = }")
# print(f"{type(y_test) = } / {y_test.shape = }")

model = DecisionTreeClassifier()

# for attr in dir(model):
#     if not attr.startswith("__"):
#         print(attr)

model.fit(X_train, y_train)

print("depth: ", model.get_depth())
print("number of leaves: ", model.get_n_leaves())

accuracy = model.score(X_test, y_test)
# print(f"{accuracy = :.4f}")
plt.figure(figsize=(20, 15))
tree.plot_tree(model,
               class_names=iris.target_names,
               feature_names=iris.featunames,
               impurity=True, filled=True,
               rounded=True)

plt.show()