Spatial Filtering
이번장은 Intensity를 다르게 변환해서 이미지를 흐리게 혹은 날카롭게 만드는 법을 배울 것이다.
그전에 신호와 시스템에 대한 기본적인 지식을 알아야한다.
Signal & Systems
Term
- Signal: 정보나 데이터의 연속 ex)밝기함수의 그래프
- System: Input Signal을 Output Signal로 변환하는 것
- System Function: System을 나타낸 함수
LTI System
- LTI(Linear Time-Invariant) System:선형적이고 시불변적인 시스템
- Linaer: 스칼라배수, 덧셈 가능한 성질
Homogeneity
Addictivity - Time-invariance(시불변성): 시간이 바뀌어도 시스템의 특성은 바뀌지 않음
Impulse, Convolution
충격으로 를 나타낸다. 한곳에만 딱 1인 신호이다.
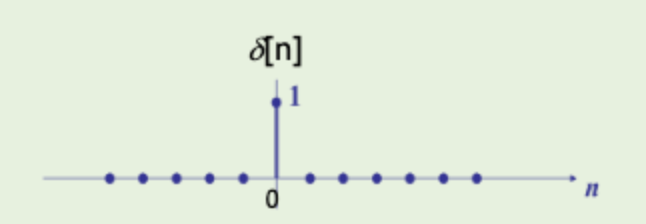
충격함수의 적분은 1이기 때문에 특정구간에서 1의 값을 가진다.
Continuous한 충격은 으로 나타낸다.
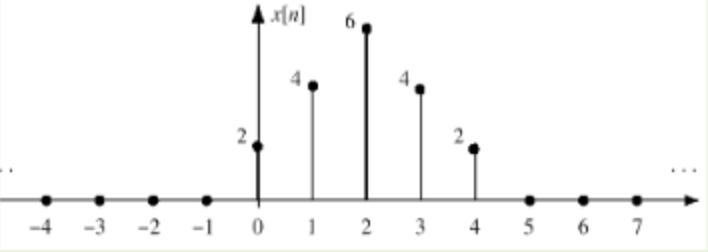
모든 이산신호는 계수와 충격함수 곱의 합으로 나타낼 수 있다.
일반 충격함수를 위의 같은 이산신호로 바꿔주는 것이 Impulse Response이다.
두 Impulse Response 에 대해
을 Convolution Sum이라고 한다.
Convolution Sum은 컴퓨터비전에서 자주 쓰이는 CNN에서 활용되기도 한다.
Spatial Domain Processing
입력 이미지 를 라는 변환작업을 통해
출력이미지 를 만드는 것을 Spatial Domain Processing이라고 한다.
Principal: Convlution
이미지를 변환할 때 사용하는 것이 바로 Convolution Sum이다.
화면을 흐리게 처리하려면 어떻게 해야할까?
색깔의 경계가 뚜렷하지 않도록 하면 흐리게 될 것이다.
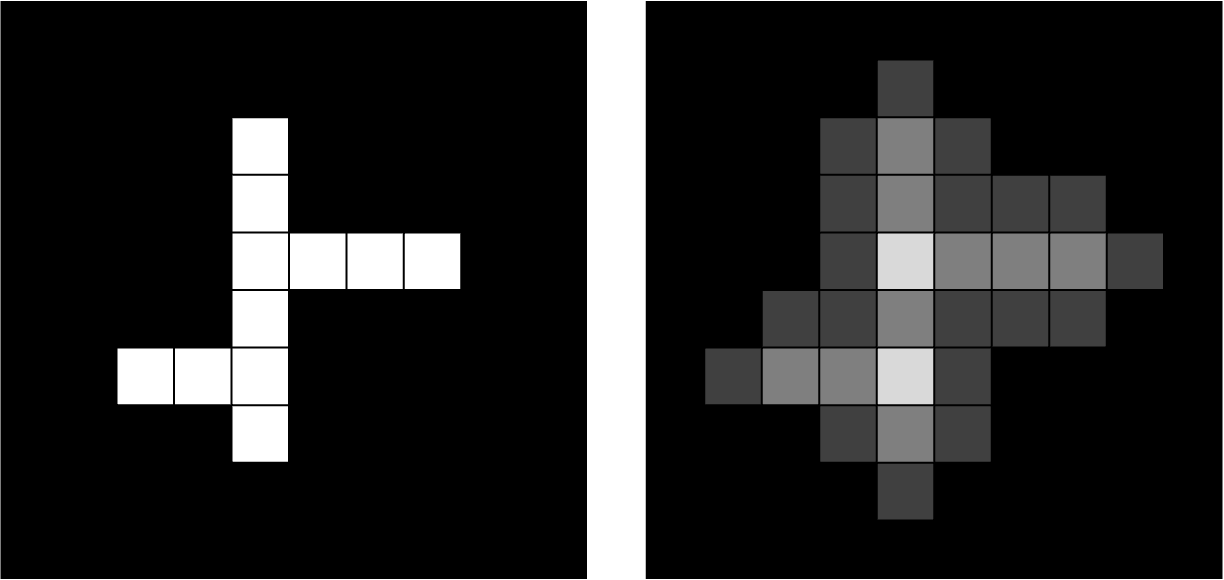
왼쪽이 원본사진, 오른쪽이 블러처리된 사진이다.
흰색 픽셀은 주변에 검은색 픽셀이 많으니 중앙값인 회색이되고,
주변에 검은색이 많은 픽셀은 좀 진한 회색이며 주변에 흰색이 많은 검정픽셀은 연한 회색이 된다.
여기서 좌측상단을 (0, 0) 그 아래픽셀을 (1, 0)으로 생각하고 (4, 4)픽셀의 주변픽셀까지 살펴보자.

(4, 4) 주변의 픽셀은 (3, 3) 부터 (5, 5)까지 자신까지포함하여 9개이다.
이를 2 Level Intensity로 고려하여 0과 1로 나타내면 다음과 같다.
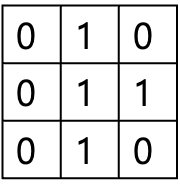
주변의 픽셀의 합은 4이고 주변 픽셀은 9개이니 4/9의 Intensity로 정할 수 있다.
이렇게 주변픽셀의 평균을 구한다.
이 과정을 수식으로 나타내면 다음처럼 나타낼 수 있다.
참고로 kernel은 3 x 3 행렬에 안의 데이터는 모두 로 차있다.
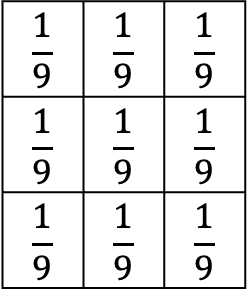
위의 식이 바로 Convolution 이다.
Linear Spatial Filtering
앞서 설명한 부분에서 원본 이미지의 주변에 곱해지는 계수들의 행렬을 Kernel이라고 하였다.
이 Kernel은 Filter, Mask, window라고 부르기도 한다.
정확한 Filtered output(Correlation)수식은 다음과 같다.
for all
그리고 주변픽셀과 자신을 반드시 포함해야하므로 커널사이즈는 반드시 홀수 이다.
Padding
끝쪽에 있는 픽셀은 주변 픽셀이 8개가 아닌데 어떻게 처리한지가 궁금할 것이다.
이때는 Padding방법을 사용하여 주변픽셀을 채운다.
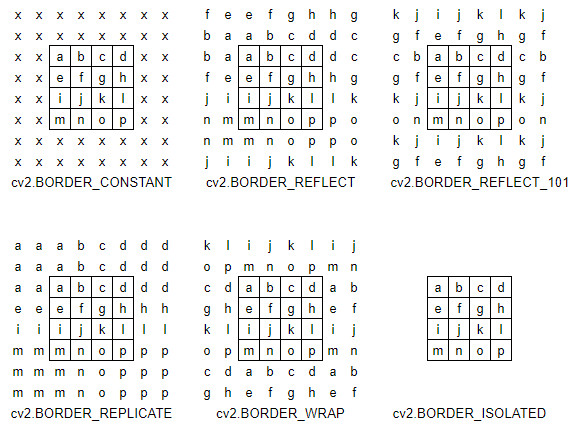
OpenCV에서는 다음의 방법을 정의한다.
- BORDER_CONSTANT: 가장자리를 정한 값으로 채움(보통 0으로 Zero Padding)
- BORDER_REPLICATE: 가장자리 값을 복사하여 채움
- BORDER_REFLECT: 가장자리 근처 값을 반사시켜 채움
- BORDER_REFLECT_101: 가장자리를 제외한 가장자리 근처값을 반사시켜 채움
- BORDER_WRAP: 화장실 타일처럼 크게 보면 타일반복처럼 채움
- BORDER_ISOLATED: 무시
Correlation & Convolution
합성곱들은 결과가 180도 회전해서 나온다.
- Correlation
for all
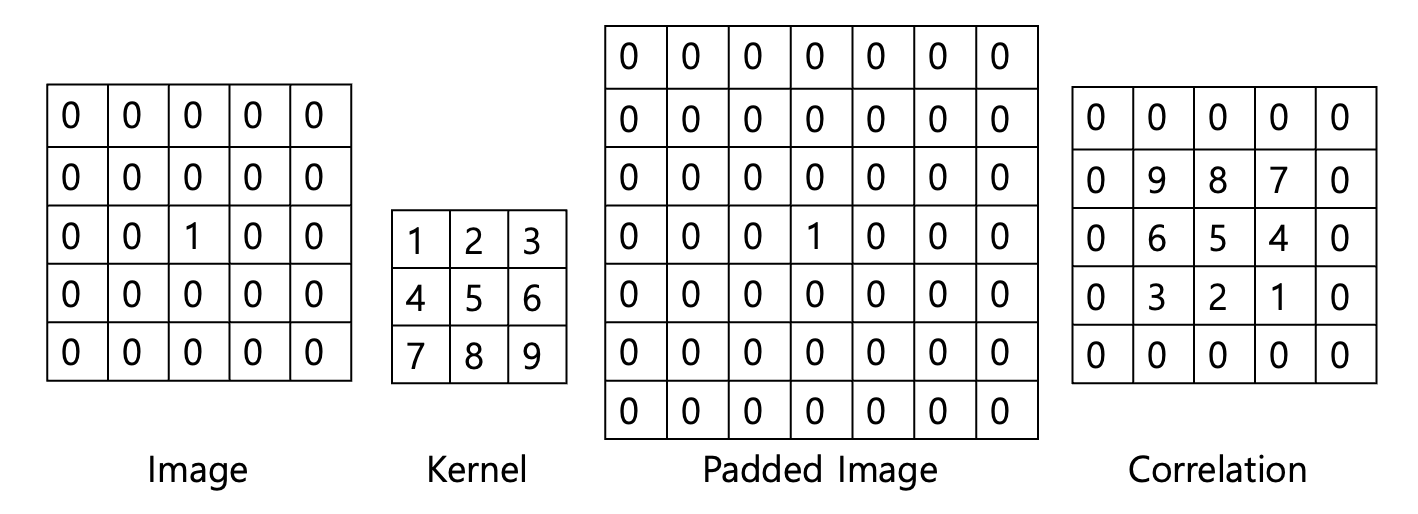
Correlation은 결과가 180도 돌아가있다. - Convolution
for all
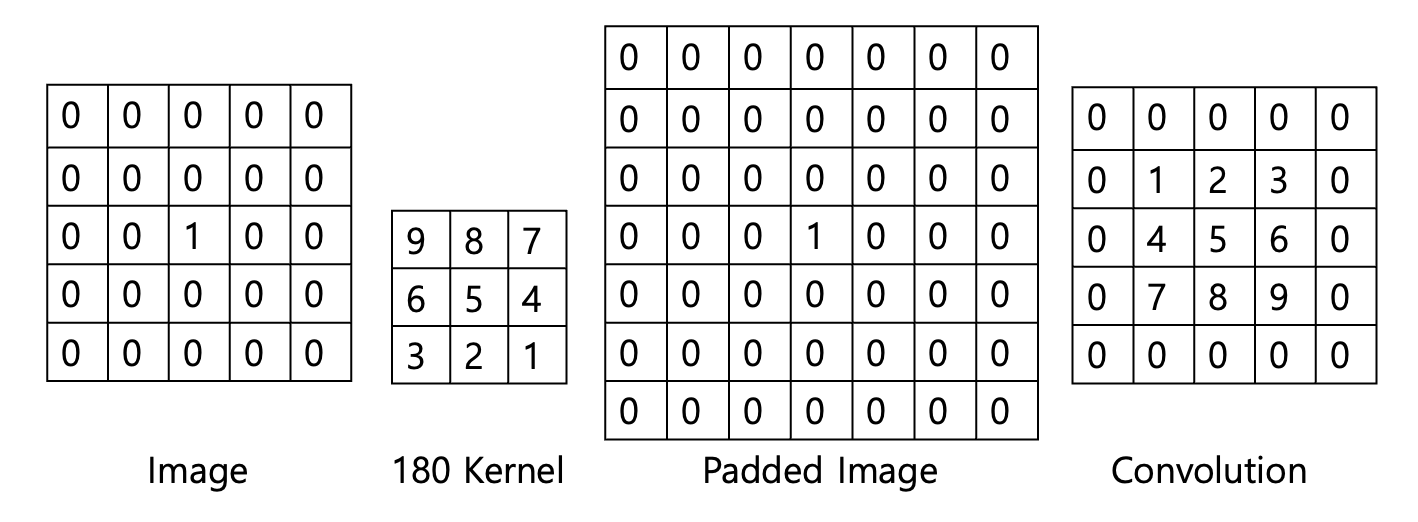
Convolution은 결과를 원본처럼 가져오기위해 Kernel을 180도 뒤집어서 연산한다.
cv2.filter2d()
OpenCV에선 원본이미지에 커널을 넣어 필터링을 하는 함수를 제공한다.

Lowpass Spatial Filters
Lowpass하다는 것은 이미지의 날카로운 부분(색과 색의 경계선)을 줄여 흐리게 만든 것이다.
흐리게 만들기에 좁쌀같은 노이즈가 들어간 이미지의 노이즈를 제거할 수도 있다.
단순히 흐리게만 변환하므로, 이미지의 총 밝기합은 변화하지 않아야한다.
즉, 커널의 계수 합은 1이 되어야한다.
다양한 방법이 있는데 설명해보겠다.
Box Filter
- 커널의 계수 합은 항상 1을 만족한다.
- 커널의 계수는 모두 일정하다.
위 조건을 만족하는 필터이다.
대표적인 커널은 아까 설명했던 이 커널이 되겠다.
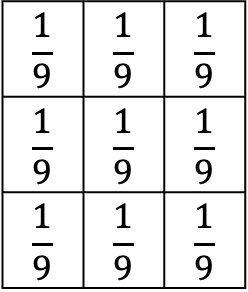
만약 window size가 5라면? 각 계수들은 가 될 것이다.
Gaussian Filter
정규분포표에 쓰는 가우시안 함수를 적용한 필터이다.
가우시안 함수는 가운데는 볼록하고 가운데와 멀어질수록 점점 줄어드는 형태이다.
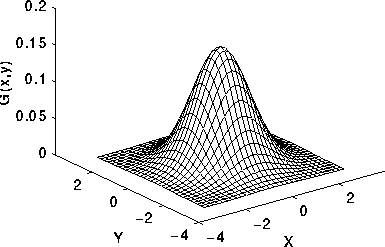
가우시안 함수는 확률이므로 PDF라 결국 적분하면 합이 1이다.
그래서 자연스레 Lowpass Filters의 성질에 만족하기도 한다.
는 계수의 합을 1로 만드는 상수이다.
이미지는 2차원이니 x축 y축 2개를 기준으로 다음의 커널이 이루어진다.
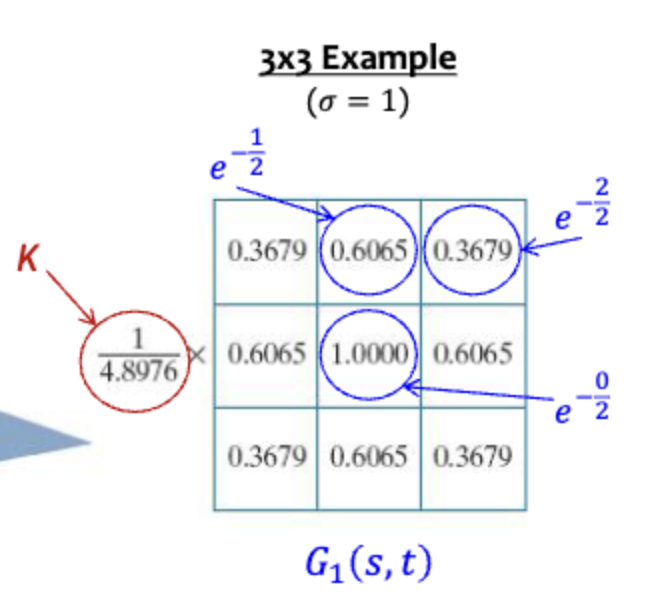
Gaussian Filter는 isotropic(원점대칭)하며 separable(분배법칙이 성립)하다.
cv2.blur()

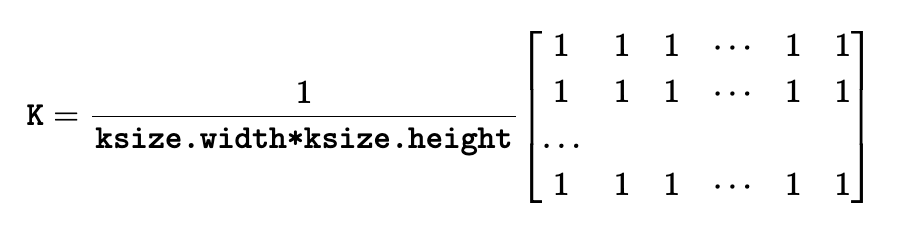
Box Filter과정으로 모든 계수의 합이 1이되도록 표현된 것이다.

Gaussian Filter는 Seperable하므로 x축 표준편차, y축 표준편차를 따로 두어 계산가능하다.
Bilateral Filtering
가우시안 필터는 화면을 Smooth하게 하며 가우시안 노이즈를 제거하는데 탁월하지만,
색과 색의 경계인 에지를 흐릿하게 하는 단점이 있었다.
그래서 거리의 차만으로 구현한 가우시안 필터에서 밝기의 차까지 도입하여 양방향 필터를 만들었다.
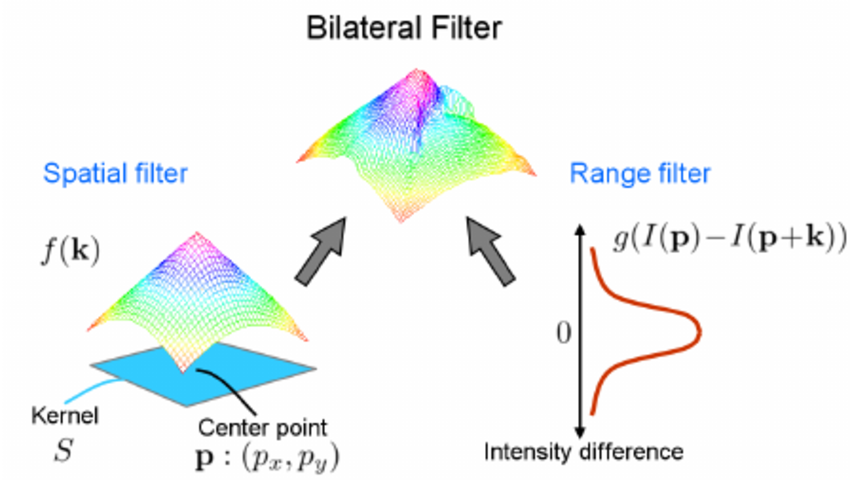
현재 픽셀과 거리가 멀수록 커널계수가 작아져 덜 반영된다.
그리고 현재 픽셀과 밝기차가 많이 날수록 커널계수가 작아져 덜 반영되는 것이다.
거리도 가깝고 색상차가 많이나면? 경계선을 최대한 살리기위해 덜 반영하는 것이다.
Bilateral Filtering은 여기에 밝기차까지 추가하여 다음의 식으로 나타낸다.
는 spatial 로 거리에 대한 표준편차이며, 은 range 로 밝기 차에 대한 표준편차이다.
cv2.bilateralFilter()

가우시안필터에서는 x, y축에 대한 시그마를 따로줬는데, 여기서는 안주는거보니까 동일하게 보는 것 같다.
Highpass Spatial Filters
Lowpass Filtering은 이미지의 Sharp 한 부분을 깎아 Smooth한 이미지를 만드는 것이라면,
Highpass Filtering은 이미지의 Sharp한 부분의 요소를 가져오는 것이다.
색과 색의 차를 줄이는 것이 아닌, 색과 색의 차를 구하는 것이다.
자연스레 미분의 개념이 적용된다.
Image in Derivatives
이미지는 결국 이산적인 데이터라서, 한 픽셀과 한 픽셀의 그 사이는 존재하지 않는다.
Continious 실수 영역에서는 Difference를 로,
Derivative는 로 표현한다.
- Forward difference
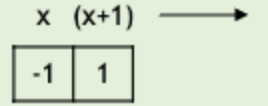
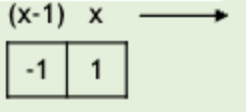
- Backward difference
Laplacian Filter
1차미분은 밝기의 변화율을 2차미분은 밝기의 변화율의 변화를 뜻한다.
말이 어렵지만 수학이나 물리때 2계도함수를 생각해보면, 위치에대한 2계도함수는 가속도를 뜻하는 말이다.
그리고 2계도함수의 값이 양수나 음수냐에 따라 아래볼록인지 위로볼록인지 판단한다.
이 2차미분 원리를 적용하는 것이다.
여기에 인 Forward difference 대입
여기에 Backward difference 계산
의 2차미분은 로
자기 양옆 픽셀을 더하고 자신을 2번뺀 값인 것이다.
이미지는 x, y축 두개이므로 편미분하여 더한다. 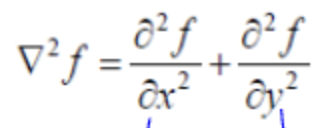
왼쪽 에 대한 식은 [1, -2, 1]이 오른쪽 에 대한 식은 이 된다.
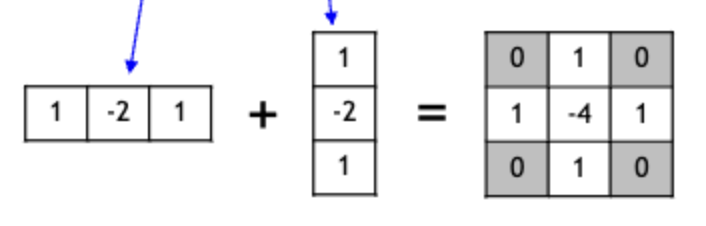
두 식을 더해 다음 형태의 커널이 바로 Laplacian Kernel이다.
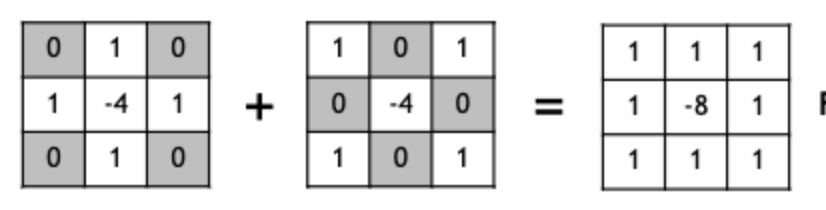
축은 +가 될 수도있고 x가 될 수도 있으며 아예 둘다더한 3번째로 커널을 사용할 수 있다.
Unsharp Masking
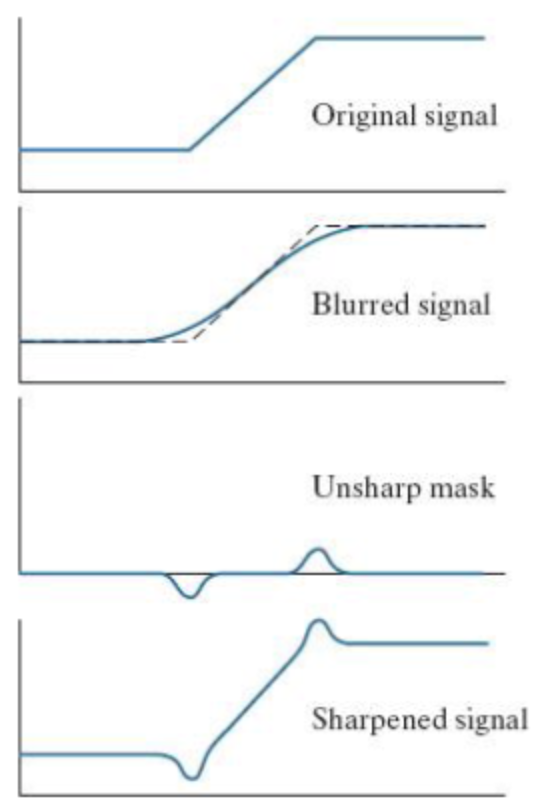
이미지에 Lowpass Filtering을 한 Blurred 이미지를 빼서 Unsharp Mask를 구한다.
이 Unsharp Mask를 다시 원본에 더하는 기법으로 이미지를 날카롭게 만들 수 있다.
- 이미지를 Blur(Box Filter, Gaussian Filter 등) 하여 를 구한다.
- 원본에 빼서 Unsharp Mask를 구한다.
- 원본에 원하는 배 만큼 Unsharp Mask를 더한다.
여기서 가 커질수록 이미지는 더 날카로워지고 작을수록 덜 날카로워진다.
음수라면? Blur먹이는 것처럼 이미지는 흐려질 것이다.
- : Unsharp Masking
- : Weakness Unsharp Masking
- : highboost filtering
이라고 부른다.
Order-Statistic Filters
값의 크기를 순서로 나열하여 필터링을 하는 기법이다.
Median Filter
평균값으로 노이즈를 제거하는 대표적인 필터인 Box Filter도 좋지만, 이 기법으로도 지워지지 않는 노이즈가 있다.
(10, 15, 20, 20, 1000)과 같은 데이터가 있다고 하자.
평균값은 213이다 그리고 크기 순으로 나열하여 가운데 값을 뜻하는 중앙값은 20이다.
만일 1000이 노이즈였다면, (10, 15, 20, 20)만으로 평균을 구해 16.25를 구할 수 있다.
중앙값을 구하는 원리가 노이즈 제거에 탁월하다는 것이다.
1000처럼 혼자 확튀는 노이즈를 salt-and-pepper noise라고 부른다.
cv2.medianBlur()

탐지할 커널사이즈를 정하여 커널안의 픽셀 Intensity 중 중앙값을 현재픽셀값으로 설정하는 원리이다.
