Denoise와 Restoration

이미지는 노이즈가 생기고 모종의 이유로 화질이 저하될 수 있다.

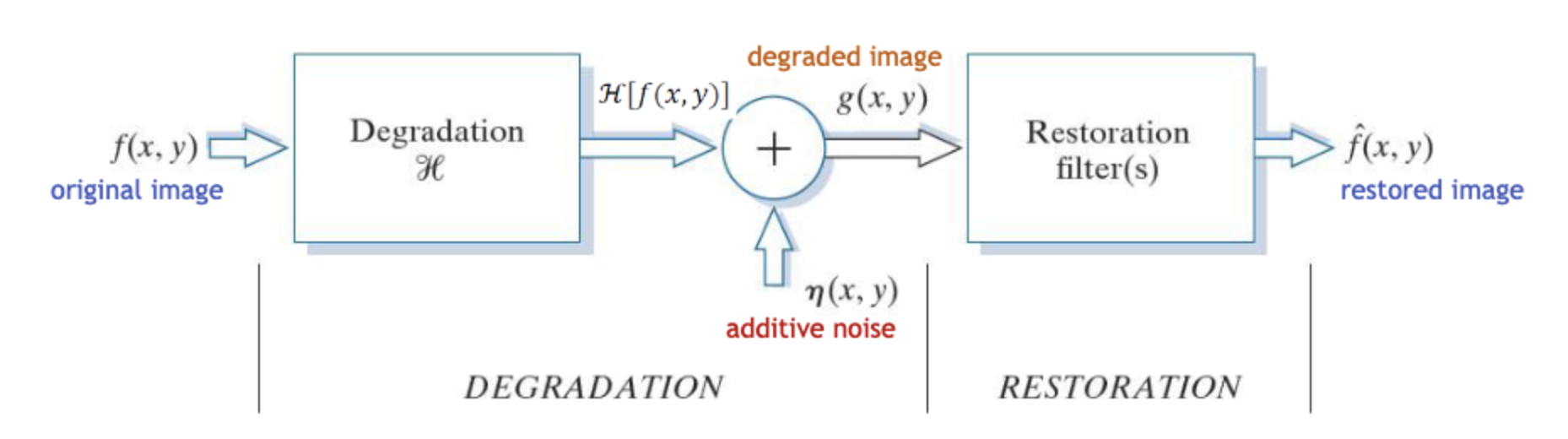
$g(x,y)=\Eta[f(x,y)]+\eta(x,y)$로 $\Eta$만큼 Degrade가 되고, $\eta$ 만큼 Noise가 추가된 이미지다.

이를 없애기 위해서는 Denoise로 $\eta$를 제거하고 Restoration으로 $\Eta$를 제거해야한다.

Noise Type

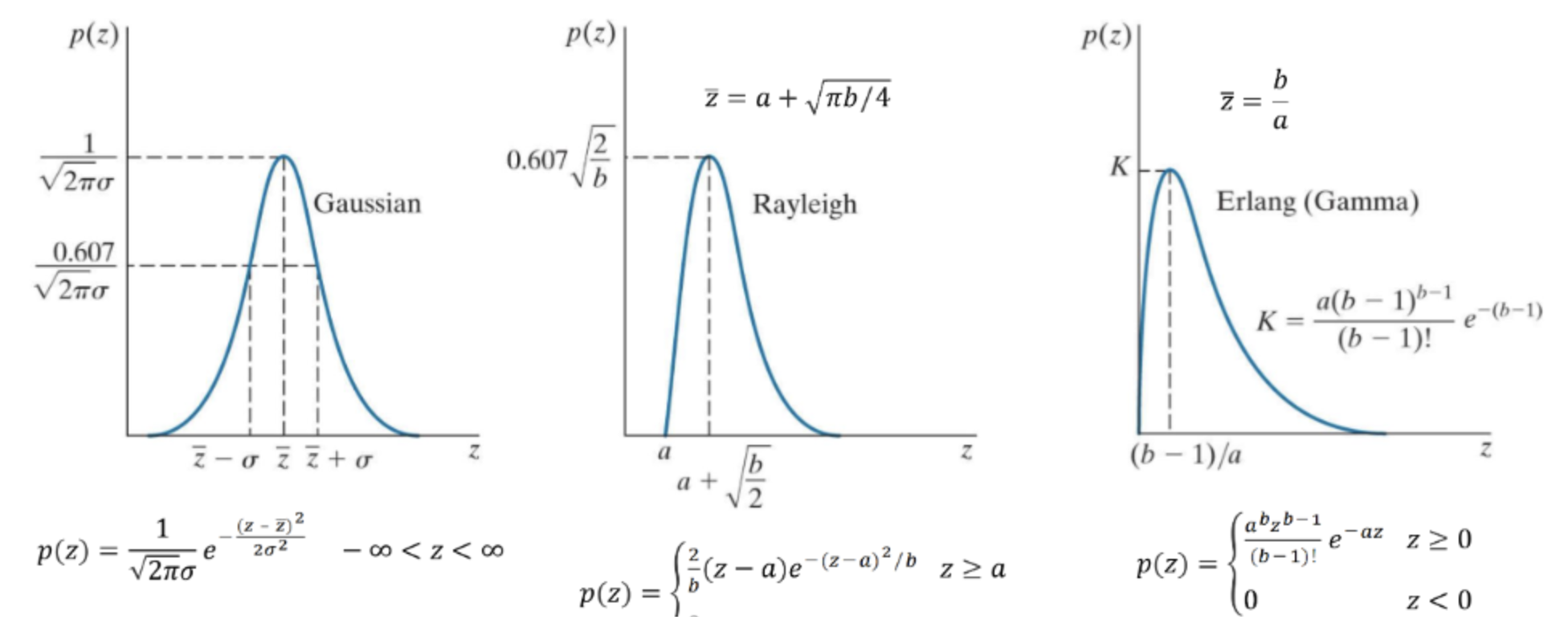
Noise에는 다양한 종류가 있다.

• Gaussian Noise
• Rayleigh Noise
• Erlang Noise
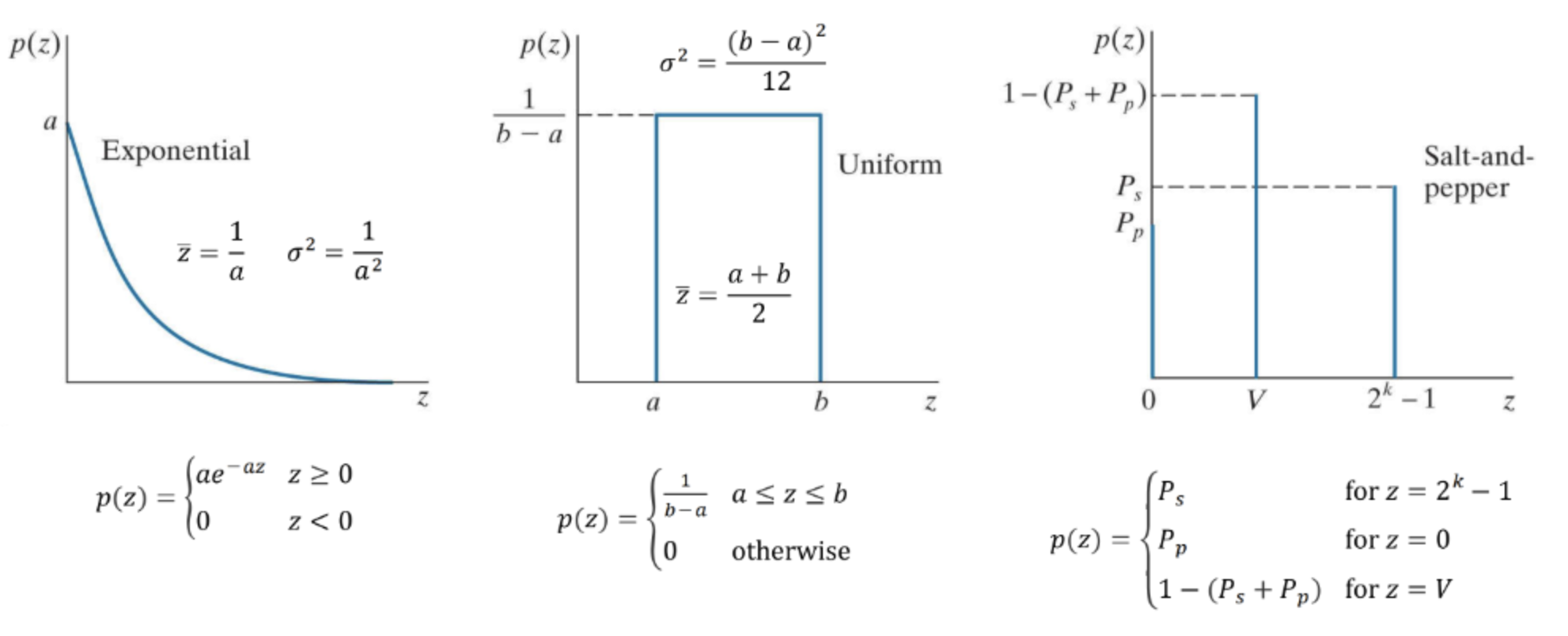
• Exponential Noise
• Uniform Noise
• Salt-and-Pepper Noise

되게 다양하지만 DFT를 하면 제거를 할 수 있다.

Method of Denoise

Frequency Domain Filter에서 배운 Ideal, Gaussian, Butterworth말고 위의 형식을 추가해서 노이즈를 fit하게 제거가 가능하다는 말이다.

mean filter

Mean filter는 Spatial Domain 에서 사용되는데, 보통 하나의 픽셀의 주변픽셀들을 sub image로 가져와 평균을 구해 대체하는 원리이다.

• Arithmetic Mean
  산술평균적인 픽셀의 값으로 만드는 것이다.

• Geometric Mean
  기하평균의 값으로 만드는 것이다.

• Harmonic Mean
  조화평균의 값으로 만드는 것이다.

• ContraHarmonic Mean
  조화평균을 보완한 것으로 Q=0이라면 Arithmetic Mean, Q=-1이라면 Harmonic Mean이 된다.
  Q>0일때는 Pepper Noise(검은색 노이즈)제거에 탁월하고, Q<0이라면 Salt Noise(흰색 노이즈)제거에 탁월하다.

Salt-and-pepper Noise의 경우는 ContraHarmonic Mean Filter를 쓰거나 Median Filter을 사용해야한다.

또한, 대부분의 주기성을 띄는 Noise는 DFT 변환시 특정 진동수를 가지고 있기 때문에, Notch Filter로 제거가 가능하다.

Degrade Type

노이즈의 종류를 봤다면, 이젠 Degrade의 종류도 있다.

• 대기 난류(전체가 흐려지는 것, lowpass filter와 유사)
  

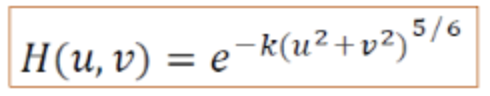
• Motion Blur
  

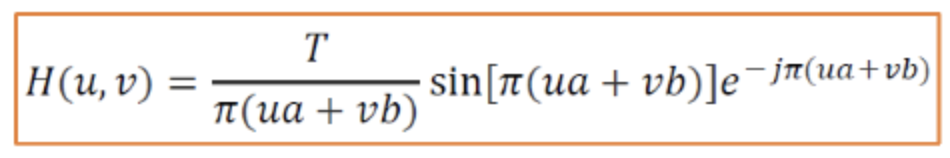
• Impulse Reponse(이미지 특정 부분의 신호가 Impulse신호와 결합)
  

오차 측정법

Restoration을 진행한 후 원본과 얼마나 정확도가 좋은지 평가할 수 있어야한다.

원본이미지와 결과이미지의 오차를 측정하는 방법은 여러가지가 있다.

• MSE(Mean Square Error)
  

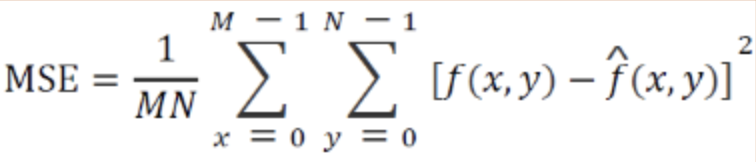
• SNR(Signal to Noise Ratio) 2가지 존재
  

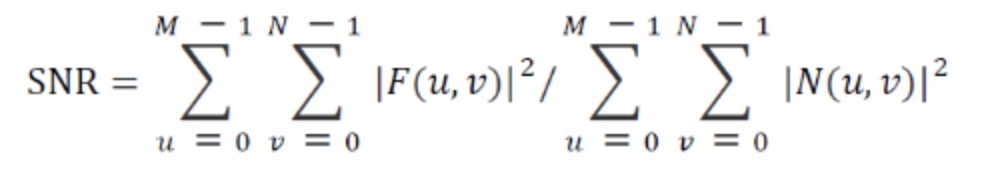
2. Spatial Domain
   

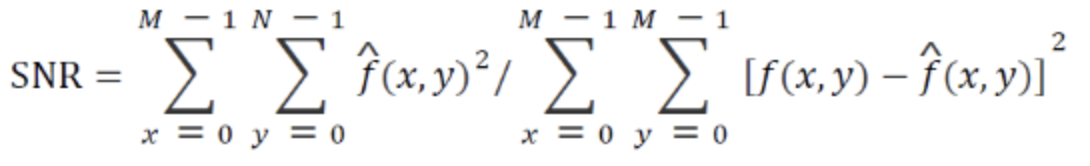
• PSNR(Peak SNR)
  

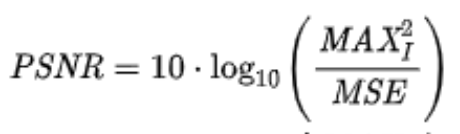
Method of Restoration

Inverse Filter

Degardation이 얼마나 일어났는지 $\Eta(u,v)$를 알고 있으므로 이 과정을 거꾸로 한다는 것이다.

Degadated Image $g(x,y)$와 Original Image $f(x,y)$에 대해

$g(x,y)=\Eta[f(x,y)]=\Eta(x,y)\times f(x,y)$가 있으면 이를 거꾸로 적용한다.

$f(x,y)=\frac{g(x,y)}{\Eta(x,y)}$가 되는 것이다.

Wiener Filter

하지만 실제로는 이미지엔 노이즈 $\eta(x,y)$가 존재한다.

$g(x,y)=\Eta[f(x,y)]=\Eta(x,y)\times f(x,y)$ 가 아니라

$g(x,y)=\Eta[f(x,y)] + \eta(x,y)=\Eta(x,y)\times f(x,y)+ \eta(x,y)$ 인 것이다.

$\hat{F}(u,v)$를 복원 이미지라고 하면 다음과 같다.

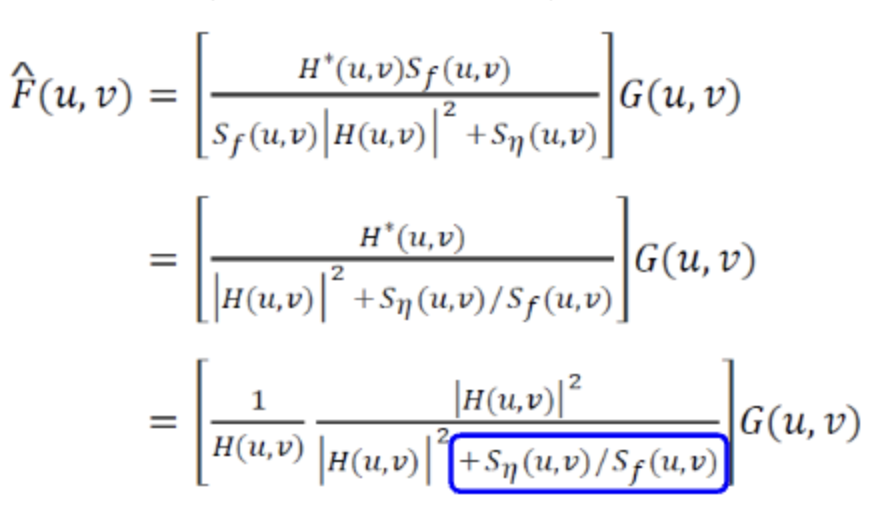
여기서 $S_{\eta}$는 Frequency Domain상 노이즈의 제곱이며 $S_{f}$는 Frequency Domain상의 Undegraded Image의 제곱이다.

노이즈가 없으면 $S_{\eta}=0$이 되어 소거법칙으로인해 $\hat{F}(u,v)=\frac{G(u,v)}{H(u,v)}$가 되어 Inverse Filter와 같아지므로, Wiener Filter는 Inverse Filter를 포함한다고 이해하면 편하다.

노이즈 $\eta(x,y)$와 Undegration의 정도 $\Eta(x,y)$를 둘다 알면 원복할 수 있다.