Abstract

양자화는 연속적인 실수 값의 집합인 신경망의 가중치 및 활성화 값을 이산 값으로 변환하여, 사용 비트 수를 줄이면서도 연산 정확도를 최대한 유지하는 기법이다.

메모리 용량이나 연산 능력이 제한된 환경에서 필수적인 기술

부동소수점 표현(float32, float16)에서 4비트 이하의 고정 정수 표현으로 전환할 경우, 이론상 메모리 사용과 지연 시간을 최대 16배까지 줄일 수 있으며, 이러한 효율성 개선은 배터리 수명 연장, 실시간 처리, 비용 절감 등 다양한 이점이 있다.

Introduction

지금까지 Overparameterized된 모델을 통해 다양한 문제에 대한 신경망의 정확도가 크게 향상되었다.
그러나, 과도하게 큰 신경망 모델은 그 크기 때문에 자원의 제약이 있는 환경에 배포하기가 어렵다.

효율적이고 실시간으로 동작하면서도 최적의 정확도를 유지하려면, 신경망 모델의 설계, 학습, 배포 방식을 고려해야 한다.

현재까지 많은 연구가 Latency, 메모리 사용량, 에너지 소비 등을 줄이면서도 정확도와 일반화 성능을 최적화하는 데 초점을 맞춰왔다.

1. 효율적인 신경망 모델 아키텍처 설계

• 아키텍처를 최적화 하는 연구
• 초기에는 수작업 탐색을 통해 새로운 최적 모듈을 찾아으나, 최근에는 AutoML, NAS를 통해 모델 크기, 깊이, 넓이 제약 하에서 최적 아키텍처를 자동으로 탐색

2. 신경망 아키텍처와 하드웨어의 공동 설계

• 신경망의 Latency와 에너지 오버헤드는 하드웨어에 따라 다르므로, 특정 하드웨어에 최적화된 아키텍처를 함계 설계하는 연구 활발

3. Pruning

• 중요도가 낮은 뉴런, 파라미터를 제거해 sparsity를 높이는 방법이다.
• Unstructured pruning은 임의 위치의 파라미터를 제거해 모델의 일반화 성능에 거의 영향을 주지 않으면서 높은 희소율을 달성하지만, 희소 행렬 연산으로 인해 메모리를 많이 사용하여 가속이 어렵다.
• Structured pruning은 모듈 단위로 제거해 밀집 연산은 유지하지만, 과도한 pruning 시 정확도 저하가 크다.

4. Knowledge distillation

• 고성능 대형 모델(teacher)가 생성한 soft label(확률 분포)를, 소형 모델(student) 학습에 활용
• 단독 distillation으로는 높은 compression이 어렵지만, 양자화, pruning과 결합하면 성능 저하 없이 compression을 크게 늘릴 수 있다.

5. Quantization

• 부동소수점 표현에서 8비트 이하의 저정밀 정수 표현으로 전환하면, 학습과 추론 모두에서 메모리, 지연 시간을 크게 줄일 수 있다.
• 특히 반정밀도(half-precision), 혼합 정밀도(mixed-precision) 학습의 도입은 AI 가속기 처리량을 획기적으로 향상시켰으나, 8비트 이하로 내리려면 섬세한 튜닝이 필요해 최근 연구는 주로 추론에 집중된다.

6. 뇌과학 관점의 Quantization

• 인간의 뇌가 연속값이 아닌 불연속(양자화) 신호로 저장한다는 연구가 있으며, 이는 noise에 강하고 자원 효율이 높다는 장점 때문이다.

개념 정리

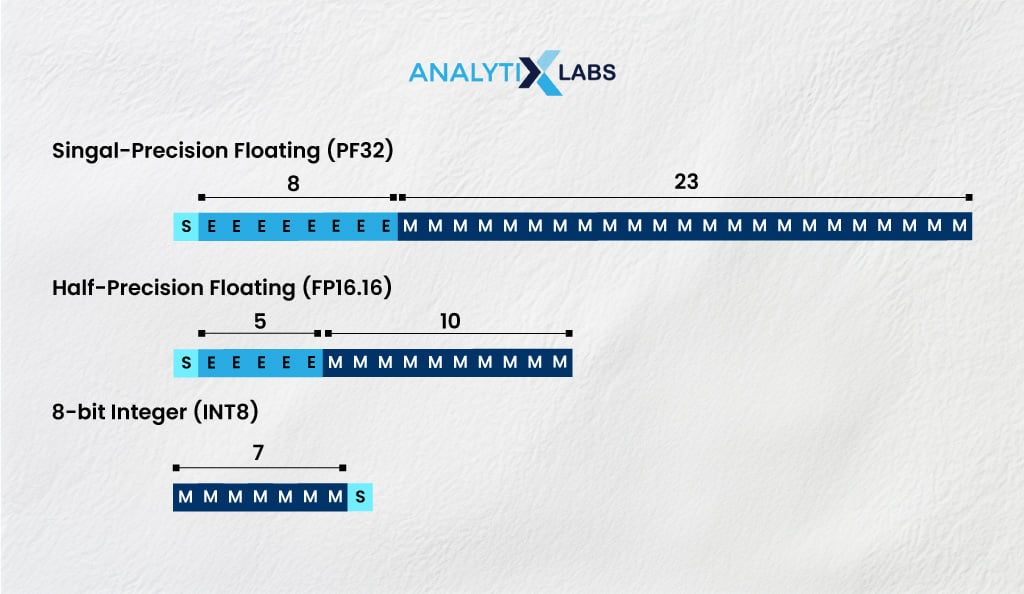
FP, INT

Floating point(FP)와 int(정수)형 표현의 큰 차이는 숫자를 내부에서 어떻게 표현하고 연산하느냐이다.

부동소수점(FP)는 아주 크거나 작은 수를 지수, 가수 조합으로 표현
정수(INT)는 소수점 없이 고정된 정밀도로 정수 범위만큼 표현

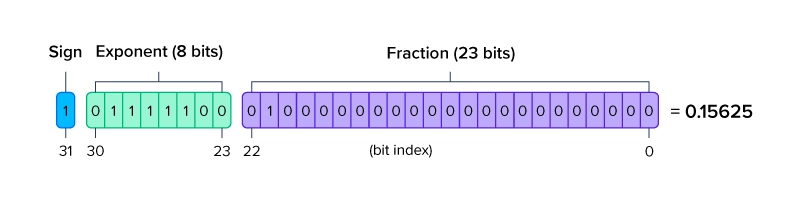
부동소수점(FP)는 부호(Sign), 지수(Exponent), 가수(Fraction)으로 구성되어 있다.

• 부호 : 값이 양수인지(0), 음수인지(1)를 나타낸다.

  ex) 0 10000001 ... -> 양수 / 1 10000001 ... -> 음수

• 지수 : 실제 지수 e에 Bias를 더한 값을 저장

  Bias는 지수 비트(0~255)로 -127 ~ 128의 범위의 e를 표현 가능하게 함

• 가수 : 1.xxxx 형태의 소수부(유효 숫자)를 저장한다.

FP32

• 비트 수 : 32bit(부호 1비트 + 지수 8비트 + 가수 23비트)
• 정밀도 : 약 7자리 십진수

FP16

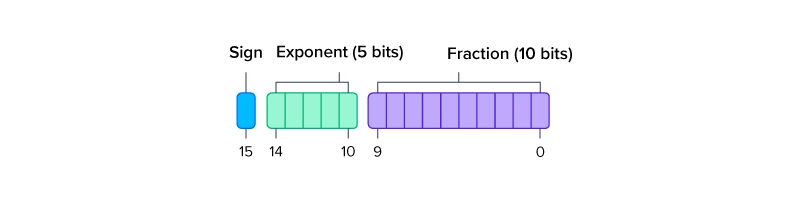
• 비트 수 : 16bit(부호 1비트 + 지수 5비트 + 가수 10비트)
• 정밀도 : 약 3~4자리 십진수

INT8

• 비트 수 : 8bit(부호 1비트 + 값 7비트)
• 정밀도 : 정수 단위

메모리 절약

같은 개수의 숫자를 저장할 때

• FP32 : 4바이트(32비트)
• FP16 : 2바이트(16비트)
• INT16 : 2바이트(16비트)
• INT8 : 1바이트(8비트)

  메모리 측면에서는 FP16과 INT16 둘 다 2바이트로 같은 개수의 값을 저장할 때 차이가 없고, 표현 방식의 차이만 존재한다.

예를 들어, 파라미터 1억 개를 저장하면
FP32는 4바이트 x 1e8 = 약 400MB
INT8은 1바이트 x 1e8 = 약 100MB (1/4 크기)

따라서, 비트 수가 적을수록 메모리 사용량이 줄어든다.

연산 속도 원리

1. 하드웨어 복잡도

FP 연산

• 덧셈, 곱셈 시 지수부 정렬, 가수 정규화, 오버플로우/언더플로우 검사 등이 필요
• 논리적으로 복잡하여 더 많은 사이클과 더 큰 전력을 소모한다.

INT 연산

• 비트가 단순하여 덧셈, 곱셈만 수행한다
• 회로가 단순하고 빠르다

2. SIMD 최적화

• INT형 연산은 CPU/GPU에서 한 번에 더 많은 요소를 병렬 처리 가능하여 한 사이클에 더 많은 연산을 처리할 수 있다.

3. 메모리 대역폭

• 전송 데이터량이 줄어들어 메모리 병목 상황에서 이득이고, 이동이 빠르다.

정확도 vs 효율성 Trade-off

• FP32 : 가장 넓은 범위의 높은 정밀도
• FP16 : FP32 대비 2배 빠르고 메모리는 절반이나, 지수, 가수 비트가 줄어들어 아주 작은 값 구분이 어려움
• INT8 : FP16 대비 2배 빠르고 메모리는 절반이나, 정밀도는 소수점 단위를 모두 버려 근사치가 크게 어긋날 수 있다.

General History of Quantization

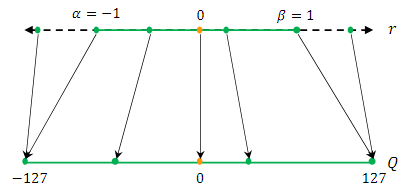
1. 초기 수치 근사 기법으로서의 양자화

양자화는 크기가 무한하거나 연속적인 값을 유한한 범위의 정수나 이산 값으로 근사할 때 사용된다.
19세기 중반부터 수치 적분 등을 위해 이산화를 이용했으며, 반올림 오차가 적분 결과에 미치는 영향을 연구했다.
즉, 반올림과 절단은 모두 양자화의 전형적 사례로, 컴퓨터가 등장하기 전에도 수치 해법에서 중요한 요소였다.

2. 정보 이론과 통신에서의 양자화 발전

1928년 정보 이론을 발표하면서, 양자화는 부호화 이론의 핵심으로 떠올랐다.
Shannon은 가변 비트 길이를 서서 효율적으로 부호를 할당하는 가변률 양자화 개념을 도입했다.
1959년에는 왜곡률과 비트율 간의 최적 절충을 다루는 왜곡률 함수와 벡터 양자화가 제안되었으며, 이후 다양한 통신 시스템과 신호 처리에 응용되었다.

3. 수치해석 관점에서의 양자화

수치해석에서는 연속 문제를 유한 비트로 다룰 때 발생하는 반올림 오차와 절단 오차가 알고리즘의 정확도와 안정성에 큰 영향을 준다.

이 두 오차는 문제의 조건수에 의해 서로 연관되며, 높은 조건수는 작은 입력 오차가 큰 출력 오차로 증폭될 수 있음을 의미한다.

양자화는 초기 수치 근사 → 정보 이론/통신의 부호화 → 수치해석의 안정성 분석의 흐름으로 발전해 왔으며, 각 분야에서 요구하는 성능에 맞춰 다양한 이론과 기법이 정립되었다.

Quantization in Neural Nets

위 주제에 관해 많은 수의 논문이 발표되었으며, 많은 사람들이 최근의 신경망 양자화 연구가 과거 연구와 어떻게 다른지 궁금해한다.

1. 계산 집약적인 신경망 inference, training 환경

전통적인 신호 처리나 수치해석에서는 계산량이 한정적이거나, 오프라인으로 처리하는 경우가 많았지만,
신경망은 inference와 training 모두 초대형 행렬 연산을 수백만 번 수행하므로, 메모리 대역폭과 연산량이 곧 실시간 성능과 직결된다.

값을 얼마나 효율적으로 표현하느냐가 신경망 전체 속도, 전력 효율을 크게 좌우한다.

2. Over-paramerization으로 인한 자유도

대부분의 현대 신경망은 수천만~수억 개의 파라미터를 갖고 있어, 원래 모델은 정확도를 조금 희생해도 파라미터를 줄이거나 비트폭을 낮춰도 성능이 크게 떨어지지 않는다.

이러한 과파라미터 구조 덕분에, 8비트, 4비트 같은 공격적인 양자화도 가능해졌고, 정확도나 복잡도 같은 지표를 잘 유지할 수 있다.

3. 순방향 오차 중심의 평가

전통적인 양자화 연구는 주로 신호 왜곡을 수치적으로 제어하면서 정확한 계산과 이산 계산 간 차이를 최소화하는 데 초점이 맞춰져 있었다.
하지만, 신경망 양자화에서는 이산화된 모델이 실제로 얼마나 잘 분류, 생성하느냐가 관심사이다.

4. 계층별 영향도를 활용한 혼합 정밀도(mixed-precision)

신경망 내부에서도 각 layer가 loss에 기여하는 정도는 다르다.
이를 활용해 중요한 layer는 8비트, 덜 민감한 layer는 4비트처럼 layer-wise로 다른 비트폭을 사용하는 mixed-precision 전략이 효과적이다.

위 4가지가 과거 연구와 달리 신경망 양자화가 갖고있는 고유한 차별점이다.

Basic Concepts of Quantization

A. Problem Setup and Notations

$L$개의 layer를 가진 신경망(Neural Network)이 각 layer마다 학습 가능한 파라미터 $\{W_1,W_2,..,W_L\}$를 가지며, 이들의 전체 조합을 $\theta$라 칭한다.

Supervised learning에서 최적화해야 할 empirical risk minimization(경험적 위험 최소화)은 다음과 같다.

$L(\theta)=\frac{1}{N}\Sigma^N_{i=1}l(x_i,y_i;\theta)$

• Train data $\{(x_i,y_i)\}^N_{i=1}$에 대해 평균 loss $L(\theta)$를 최소화하도록 $\theta$를 학습
• Loss function $l(⋅)$은 task에 따라 MSE, Cross Entropy 등 사용

  • $(x_i,y_i)$는 입력 데이터와 그에 대응하는 정답 label(Supervised learning)
  • $N$ : 전체 데이터 포인트 수

또한, $i$번째 layer의 input hidden activation을 $h_i$, output hidden activation을 $a_i$로 정의해 둔다.

현대의 Neural network는 크고 복잡하며, 32비트 부동소수점으로 pre-training된 모델 파라미터 $\theta$를 갖고 있기 때문에 메모리, 연산량 측면에서 부담이 크다.

Quantization의 목표는 이 파라미터 $\theta$뿐만 아니라, 중간 activation 값들($h_i,a_i$)까지도 최소한의 정확도 손실만을 남기면서 저비트로 바꾸어 모델 경랼화 및 추론 속도를 향상시키는 것이다.

이를 위해, floating point 값을 양자화된 int값으로 mapping시켜주는 Quantizaton operator(양자화 연산자)를 정의해야 한다.

이 과정에서 모델의 accuracy가 크게 떨어지지 않도록 하는 것이 관건이다.

B. Uniform Quantization

먼저, Neural network의 가중치와 활성화 값을 유한한 값의 집합으로 Quantization할 수 있는 양자화 함수를 정의해야 한다.(Quantization operator/function)

이 함수는 Floating point값을 받아서 더 낮은 정밀도의 범위(Int)로 매핑한다.

널리 사용되는 Quantization function은 다음과 같다.

$Q(r)=Int(r/s)-Z$

• $Q(r)$ : Quantization operator, 양자화된 정수 값
• $Int$ : 정수로 변환하는 함수(반올림 함수 등)
• $r$ : 실수(Floating point) 입력값(가중치, 활성화 값)
• $S$ : 실수 값의 scaling 인자
• $Z$ :정수(Int)형 zero point

  Zero point?

  실수 $r$을 정수로 바꾸는 데 있어서, 0이 어떤 정수로 매핑되어야 할지를 지정해 주는 값

  • $Z=0$이면 중심이 0으로 대칭 양자화
    
  • $Z≠ 0$이면 중심을 살짝 옮겨서 비대칭 양자화
    

이 함수는 실수 $r$을 정수 값으로 매핑하는 함수이다.

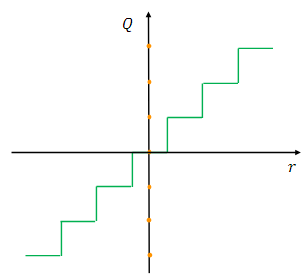
이러한 Quantization 방식은 Uniform Quantization(균등 양자화)라고 불린다.

양자화된 값이 균등한 간격으로 배치되기 때문이다.

균등한 간격?

양자화된 값들 사이의 간격이 모두 일정한 상태로, 변환 전 실수 값들을 균들한 간격으로 변환시킨 경우 나타난다.

한편, 비균등 양자화(Non-uniform Quantization) 방법도 존재하는데, 이 경우 양자화된 값들이 균등하게 배치되지 않을 수 있다.

---

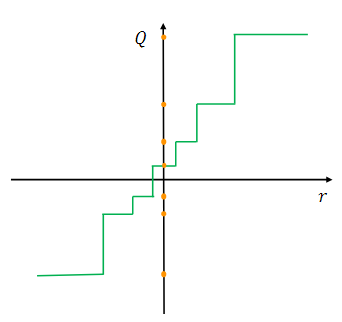
양자화된 값 $Q(r)$로부터 다시 실수 $r$로 복원하는 것도 가능한데, 이를 비양쟈화(Dequantization)이라고 한다.

$\tilde{r}=S(Q(r)+Z)$

• $Q(r)$ : Quantization operator, 양자화된 정수 값
• $Z$ :정수(Int)형 zero point
• $S$ : 정수를 다시 실수로 늘려주는 scaling 인자
• $\tilde{r}$ : 양자화된 값을 기반으로 다시 실수로 바꾼 실수 값

여기서 복원된 실수 $r$은 반올림 연산으로 인해 원래 값 $r$과 정확히 일치하지 않을 수 있다.

C. Symmetric and Asymmetric Quantization

Uniform Quantization에서 중요한 요소 중 하나는 $Q(r)=Int(r/s)-Z$의 scaling 인자 $S$의 선택이다.

이 scaling 인자 $S$는 주어진 실수 값 $r$의 범위를 여러 개의 구간으로 나누는 역할을 한다.

$S=\frac{\beta-\alpha}{2^b-1}$

• [$\alpha,\beta$] : 클리핑 범위로, 실수 값이 너무 넓게 퍼져 있으면, 정수로 표현할 때 오차가 커지기 때문에 실수 값을 일정한 범위 안으로 잘라내는(cliping) 작업 수행
• $b$ : 양자화 비트 수(bit width)로, INT8이면 $b$=8, 총 256개의 정수

따라서, Scaling 인자 $S$를 정의하려면 먼저 Cliping range [$\alpha, \beta$]를 정해야 한다.

이 Cliping range를 선택하는 과정을 Calibration이라고 부른다.

간단한 선택 방법은 값의 최소/최댓값을 이용하여 Cliping range를 설정하는 것이다.

• $\alpha=r_{min}$
• $\beta=r_{max}$

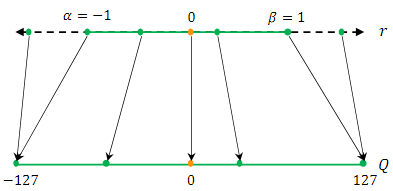
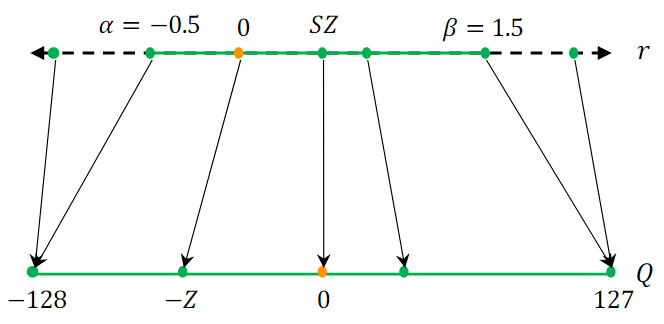
이러한 방식은 비대칭 양자화(Asytmmetric quantization) 접근법에 해당한다.

왜냐하면, 이 Cliping range는 원점 0을 중심으로 대칭적이지 않기 때문이다.

즉, $-\alpha ≠ \beta$인 경우이다

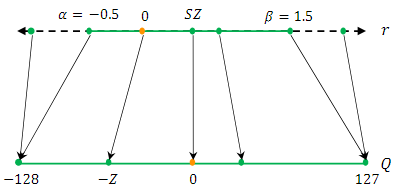
반면, $-\alpha = \beta$로 대칭적인 cliping range를 설정하여 대칭 양자화(Symmetric Quantization) 방식을 사용할 수도 있다.

입력 값의 최댓값과 최솟값의 절댓값 중 더 큰 값을 기준으로 $-\alpha = \beta=max(|r_{max}|,|r_{min}|)$으로 설정한다.

비대칭 양자화는 대칭 양자화에 비해 더 좁은 Cliping range를 얻는 경우가 많다. 이는 특히 가중치나 활성화값이 비대칭적일 때 유리하다.

대칭 vs 비대칭 cliping range

예를 들어, 실수 값이 [0,5]에 몰려 있는데 대칭 양자화의 경우 cliping range가 [-5,5]로 10의 범위 폭을 갖지만, 비대칭의 경우 [0,5]로 범위 폭이 절반으로 줄어든다.

실제 데이터 분포에 맞게 필요한 만큼의 범위만 쓰기 때문에 비대칭이 더 효율적

좁은 Cliping range가 왜 중요?

양자화에서는 Cliping range가 좁을수록, 정해진 비트 수로 더 촘촘하게 값들을 표현할 수 있다.
즉, 정수 하나당 더 정밀한 실수값 표현이 가능하다

한편, 대칭 양자화를 사용하면 $Q(r)=Int(r/s)-Z$의 수식을 더 단순화할 수 있다.
이 경우, Zero point $Z$는 0으로 설정된다.

$Q(r)=Int(r/s)$

여기서, Scaling 인자 $S$를 설정하는 방식은 두 가지가 있다.

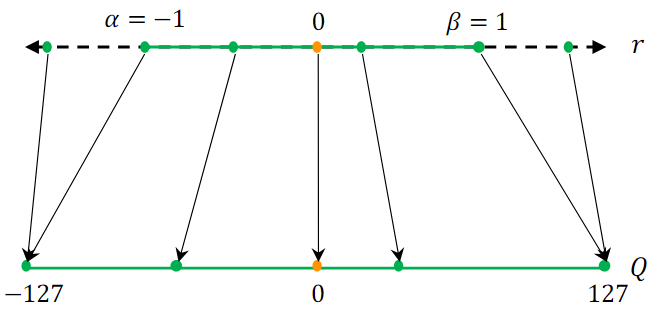
• Full range 대칭 양자화

  $S=\frac{2max(|r|)}{2^b-1}$

  • $-max(|r|)(128) + max(|r|)(127) = 255$

  INT8 범위 [-128,127]을 모두 사용(반올림 모드 필요)

• Restricted range 대칭 양자화

  $S=\frac{max(|r|)}{2^{b-1}-1}$

  • max(|r|) = 127

  [-127,127] 범위만 사용

Full range 대칭 양자화를 사용하는 방법은 더 정확하며, 실제로 대칭 양자화는 구현이 간단하고 Zero point를 0으로 둘 수 있어 많이 사용된다.

Full 이랑 Restricted는 딱 1차이밖에 안 나는데, 기술적 관점에서 큰 차이?

INT8의 경우 -128~127의 범위를 갖기에 비대칭 구조를 띈다.
그래서, -128은 딱 하나뿐인 "특이한 값"이 된다.

주로 -128은 에러 표시, 패딩, 마스킹 등 특정 용도를 갖고 사용하게 되는데 이로 인해, 성밀도은 높일 수 있지만 -128이란 값으로 인해 버그나 오버플로우가 생길 수 있다.

이 오류는 심각할 수 있기에 대부분 -127까지의 restricted range를 사용한다.

반면, 비대칭 양자화는 Zero point가 0이 아니기 때문에 offset이 발생한다.

최소/최댓값 사용에 대한 논의점

대칭 및 비대칭 양자화 모두에서 값의 min/max를 사용하는 방식은 매우 일반적이지만, 이 방식은 활성화 값 내의 outlier(이상치)에 민감하다는 단점이 있다.

이상치는 범위를 불필요하게 넓게 만들고, 결과적으로 양자화의 해상도를 떨어뜨릴 수 있다.

해결 방법

• Percentile(분위율) 사용

  가장 큰 값이나 가장 작은 값 대신, i번째로 큰 값을 $\beta$, i번째로 작은 값을 $\alpha$로 사용하는 방식이다.

• KL divergence

  실수 값과 양자화 값 사이의 정보 손실을 최소화하도록 $\alpha$와 $\beta$를 선택하는 것이다.

D. Range Calibration Algorithms: Static vs Dynamic Quantizatio