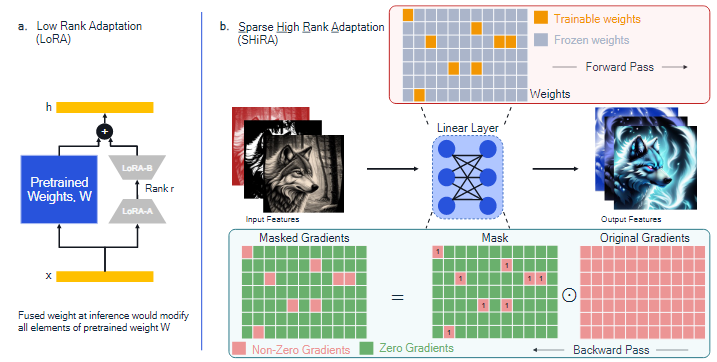
Abstract

생성형 AI research에서 LoRA 기법이 크게 주목받고 있다.
LoRA의 주요 장점은

• pre-training된 모델과 결합할 수 있어서 inference 오버헤드는 피할 수 있다.

하지만,

• adaptor를 빠르게 교체하기 어렵고
• Base 가중치와 결합하지 않을 경우, adapter의 빠른 교체가 가능하지만, inference에서 latency가 발생한다.

이러한 문제를 해결하기 위해 Sparse High Rank Adapters(SHiRA)를 제안한다.

• Inference시 오버헤드 없음
• 빠른 Adapter 교체 가능

SHiRA는 전체 가중치 중 1~2%만 직접 조정하고, 나머지는 그대로 두어 sparse한 adapter를 생성한다.

1. Introduction

LoRA는 대규모 generation 모델을 efficient하게 tuning하기 위해 확립된 기법이다.
LoRA는 fine-tuning과정에서 매우 적은 메모리를 사용하지만 성능이 우수하다.

<LoRA의 한계>
1. 대규모 모델 배포 문제

LoRA 파라미터를 pre-training된 가중치에 결합하면 전체 가중치 행렬이 변경되는데, 대규모 모델을 on-device에 배포할 경우, inference 시 많은 가중치를 변경해야 한다.

저장가능한 메모리가 매우 작아, 모든 layer의 가중치를 한 번에 불러올 수 없어, LoRA의 각 layer 별로 가중치를 불러오고 수정하는 과정을 반복하는 과정에서 latency가 발생한다.

2. 빠른 adpater 교체의 어려움

   메모리가 제한된 환경에서는 모든 가중치를 한 번에 저장할 수 없기 때문에, Adapter의 교체가 필요한 경우에, latency가 크게 증가한다.

   다른 adapter 사용 시, 기존 adapter를 해제하여 base 모델의 가중치로 다시 돌린 뒤, 다른 adapter를 적용해야 하기 때문에 latency 발생

3. Unfuse 모드의 성능 저하(결합하지 않고 Inference)

   Tuning된 LoRA의 가중치를 base weight에 결합하지 않고 inference시에 inference 경로에 LoRA 연산이 추가되기 때문에 base모델 대비 30%의 latency가 발생한다.

4. 개념 손실

   여러 개의 Adaptor를 단순히 합산해서 사용할 경우, 각 adaptor가 학습한 개념이 서로 간섭하여 일부가 손실되는 현상이 발생할 수 있다.
   LoRA는 가중치 전체에 대해 tuning하기 때문에, 서로 다른 adaptor간 수정하는 영역이 크게 겹치게 된다.

5. High rank adapter의 가능성

   "Damjan Kalajdzievski. A rank stabilization scaling factor for fine-tuning with lora. arXiv preprint arXiv:2312.03732, 2023."에서 High rank adapter가 Low rank adapter보다 더 높은 표현력을 가지며, 올바른 scaling을 적용하면 성능이 훨씬 좋아질 수 있다고 보고했다.

   LoRA는 구조적으로 rank가 낮기 때문에, 복잡한 개념이나 다양한 스타일을 동시에 학습/표현하는 데 한계가 존재한다.

따라서, 이 논문에서는 다음과 같은 주요 문제를 다룬다.

1. Base 가중치에 결합된 adapter에 대한 빠른 전환을 어떻게 수행할 수 있는가?
2. 여러 개의 adapter를 결합할 때, 개념 손실을 줄일 방법은 없는가?
3. Training/Inference 비용을 크게 늘리지 않고도, 표현력이 높은 high rank adapter를 만들 수 있는가?

SHiRA는 위의 세 문제를 해결한다.

핵심 Contribution

• Pre-training된 가중치의 1~2%만 tuning해도 LoRA보다 뛰어난 성능을 발휘하는 매우 sparse하지만 high rank의 adapter
• LoRA처럼 모든 가중치를 수정하지 않아 inference 시 교체할 파라미터의 수가 적어 빠른 속도의 adapter 교체 가능
• 높은 spasity 덕분에 여러 개의 adapter 결합 시 수정되는 위치의 중복 확률이 낮아져 개념 손실 감소
• SHiRA는 LoRA만큼 빠르게 training하면서도 GPU 메모리를 더 적게 사용한다.

2. Background and Related Work

2.1 Background: Edge Deployment Challenges for LoRA

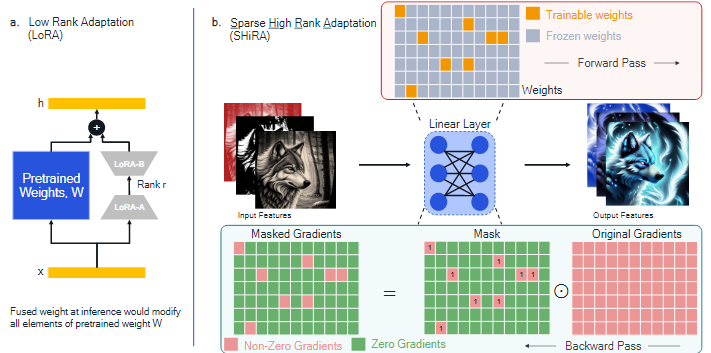
LoRA의 기본 배포 옵션은 세 가지가 존재한다.

1. Adapter를 base model과 결합한 뒤 device에 배포

   이 방법은 base model과 비교했을 때, 가중치 행렬의 상당 부분이 변경되기 때문에 DRAM의 트래픽이 증가하여 Adapter의 빠른 전환이 어렵다

   • 사전에 LoRA 가중치를 결합해 두면 실행 속도는 빠를 수 있지만, Adapter를 변경할 때, 전체 가중치 행렬을 다시 수정해야 해서 DRAM의 전송량이 커지고 전환 속도가 느려진다.

2. Adapter를 결합하지 않은 상태로 유지

   이 방법은 base model에 결합하지 않았기 때문에, adapter의 빠른 전환이 가능하지만, inference 시 base model의 가중치 + LoRA의 가중치로 추가 연산이 생겨 latency가 증가한다.

3. Hugging face/Diffusers 파이프라인 사용

   • load -> fuse -> inference -> unfuse -> unload

   1. 먼저, LoRA의 저랭크 행렬 A, B 가중치를 로드한 뒤,
      $W_{new}=W+AB$의 형태로 가중치를 결합하여 inference에 사용한다.
   2. 이후, adapter를 교체할 때, $W=W_{new}-AB$로 되돌린 뒤, 기존 LoRA 가중치를 unload하고 새 adapter를 load하여 $W_{new}=W+AB$의 형태로 다시 가중치를 결합한다.

   이 방법은 loading과 fuse를 매번 수행해야 하는데, 메모리가 제한된 환경에서 모든 가중치를 한 번에 load할 수 없어 layer단위로 처리해야 하고, 그만큼 latency가 증가하게 된다.

즉, 기존 LoRA는 Adapter의 빠른 전환, 낮은 latency, 적은 메모리 사용을 동시에 만족시키기 어렵다는 문제가 존재한다.

2.2 Related Work

LoRA, its variants, and sparse adapters

다양한 LoRA의 변형들인 저랭크 학습 방법(DoRA, VERA,..)들이 존재하지만, SHiRA의 핵심 차이점은 training/inference 비용을 늘리지 않으면서도 high rank의 adapter라는 점이다.

또한, 기존 방법들의 경우, 최종적으로 결합된 adapter는 pre-training된 가중치 행렬의 모든 요소를 업데이트하기 때문에 빠른 전환이 불가능하다.

---

일부 LoRA 변형 adapter들은 sparsity와 low rank adaptation을 결합하는 접근을 시도했었다.

1. Sparse-adapters

   Unstructured pruning 기법을 이용해 adapter를 잘라내어 효율성을 높임

2. SoRA

   LoRA의 up/down projection(기존 차원->r / r-> 기존 차원) layer에서 요소들을 gating(proj 행렬의 특정 요소에 대해, 얼마나 중요한지를 판단하는 gate 값을 두고 중요도가 낮은 특정 차원은 0으로 만듦)하고, inference 시 0의 값을 잘라내는 adaptive rank 방법 제안

3. RoSA

   Low rank adapter에 일부 High rank 특성을 결합한 방법으로, SoRA의 방법(gating)에 특정 차원은 rank를 높이는 방향의 조정이 들어간 방법이다.

하지만, 이 방법들은 모두 LoRA와 결합한 방법이기 때문에, 결합된 adapter의 가중치는 pre-training된 가중치 전체를 덮어쓰게 된다.

Partial Finetuning

SHiRA는 LoRA 이전에 제안되었던 부분적 미세조정(partial fine-tuning) 기법과 연관이 있다.
Partial fine-tuning은 고정된 sparse mask나 학습된 mask를 이용하여 fine-tuning한다.

LoRA 기반 방법과 비교했을 때, partial fine-tuning의 가장 큰 한계점은 높은 GPU 메모리 소비로, 대규모 generation 모델에 적용하기 어렵다.
LoRA의 성공의 이유 중 하나는 이를 해결했다는 점이다.

SHiRA는 LoRA만큼 efficient하게 training하면서도, 이전의 partial fine-tuning보다 훨씬 더 적은 메모리를 사용하는 adapter를 제안한다.

---

또 다른 주목할 만한 연구로는 partial fine-tuning을 LLM에 확장하였으며, LoRA와 비슷한 속도와 메모리를 제공한 "SpIEL"이 있다.

• SpIEL vs SHiRA

  1. SpIEL은 dynamic mask를 사용하지만 SHiRA는 static mask를 사용한다.

     SpIEL의 dynamic mask를 사용하기 위해서는 GPU용 custom linear layer 커널을 설치해야 하지만, SHiRA의 static mask는 custom 커널을 설치할 필요 없이, pytorch에서 직접 작동한다.

     SHiRA의 가장 큰 장점은 training/inference가 쉽다는 점이다

  2. SpIEL에서 다루지 않았던 multi adapter 결합에 대한 속성을 분석한다.

  3. SpIEL은 Language task에 대해서만 다루지만 SHiRA는 Vision/Language task 모두에 대해 다룬다.

Multi-Adapter Fusion

기존의 multi adapter 결합 방법은 개념 손실을 방지하는 데 중점을 둔다.
하지만, 이러한 방법은 기본적인 LoRA를 그대로 사용한 다음, 간단한 후처리를 수행하거나 약간의 변형을 만든다.

SHiRA는 여러 개념들이 자연스럽게 서로 간섭하지 않도록, 개념 손실 문제에 대한 새로은 adapter를 도입하였다.

이러한 기술을 사용하여 adapter를 추가로 후처리할 수 있기 때문에 SHiRA는 이전의 multi adapter 결합과 다르다.

3. Proposed Approach

3.1 Sparse High Rank Adapters (SHiRA)

SHiRA는 pre-training된 모델에서 매우 sparse하게 trainable parameter를 활용한다.

LoRA처럼 forward과정에서 새로운 가중치 행렬을 추가하지 않고, 기존 가중치의 일부만 training할 수 있도록 masking하여 학습한다.

이를 위해, 매우 sparse한 형태(98~99% sparsity)의 mask $M을 생성한다.

$M\in \R^{n\times m}=\{0,1\}^{n\times m}$

• $n, m$ : SHiRA를 적용하는 모듈의 가중치의 input/output dimension
  
  $n\times m$크기의 가중치 행렬에 0,1의 binary mask를 생성하는 것이다.

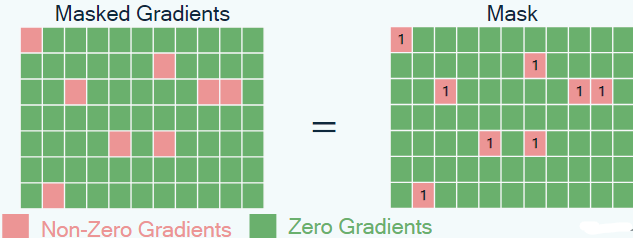
이렇게 만들어진 mask $M$은 Hadamard 곱셉을 사용하여 backpropagation 과정에서 Gradient를 masking하는 데 사용된다.

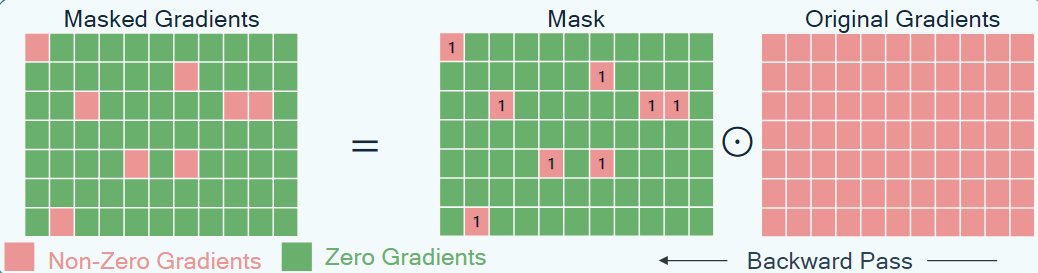
따라서, training 중에 업데이트되는 파라미터는 거의 없으며, adapter는 sparse한 가중치로만 구성된다.

• <SHiRA의 mask를 만드는 기법>

1. SHiRA-Struct

   특정 행/열만 trainable하게 structured 형태로 생성한다

2. SHiRA-Rand

   1~2%의 파라미터를 random하게 trainable하게 설정한다.

3. SHiRA-WM

   각 layer에 대한 weight magnitude을 기준으로 top-k만 trainable하게 설정한다.

4. SHiRA-Grad

   작은 calibration set에서 gradient를 수집하여 가장 크기가 큰 1~2%만 trainable하게 설정한다.

5. SHiRA-SNIP

   Pruning 기법인 SNIP을 사용하여 weight magnitude와 gradient를 결합한 방법이다.

3.2 Rapid Adapter Switching, Multi-Adapter Fusion, and High Rank

SHiRA 학습 과정에서 변경되는 가중치는 매우 적기 때문에, 이를 추출하여 trainable 가중치의 값과 해당 인덱스를 저장할 수 있다.

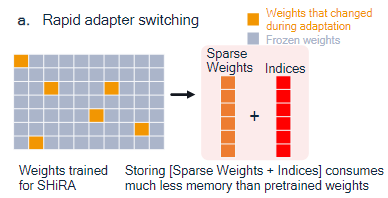
따라서, SHiRA는 LoRA와 모델 크기는 비슷하지만, inference 시 pre-training된 가중치의 일부만 덮어쓴다.

반면, LoRA는

$W_{new}=W+AB$

의 형태로 가중치를 결합하여 pre-training된 가중치 전체를 수정한다.

SHiRA의 경우, 전체 결합을 할 필요가 없고, 수정된 값만 pre-training된 가중치 행렬의 올바른 인덱스에 덮어쓰면 되기 때문에
리소스가 제한된 장치에서 빠른 adapter 전환이 가능하다.

---

SHiRA에서 multi adapter 결합을 한다면,
두 개의 adapter $A_1,A_2$가 sparse mask $M_1,M_2$를 가질 때
다음과 같은 질문을 할 수 있다.

1. Sparsity가 multi adapter 환경에서 adapter간 상호 간섭에 미치는 영향은 무엇인가?

   서로 간섭하지 않는 adapter를 만드는 것은 개념 손실을 피하기 위해 필수적이다

2. Inference 시 adapter간 간섭이 거의 없도록, SHiRA 가중치를 만드는 mask를 설계할 수 있는가?

   이론적으로, SHiRA-Struct 방법은 orthogonal하게 adapter를 만들 수 있다.

4. Theoretical Insights for SHiRA

4.1 Rank vs. Sparsity

Lemma 4.1

SHiRA의 매개변수 복잡도와 학습 복잡도는 adapter에서 0이 아닌 원소의 개수와 동일하다.

SHiRA에서 학습해야 하는 건 sparse matrix의 1의 위치 값이다.
이 값들의 개수를 $L_0 norm(||\Delta W||_0)$으로 세면, 매개변수의 수가 된다.

$L_0 norm(||\Delta W||_0)$은 0이 아닌 원소의 개수를 세는 연산으로 학습해야 하는 파라미터 수는 $||\Delta W||_0$가 되는 것이다.

• 왜 $||\Delta W||_0$가 학습 복잡도인가?

  학습 복잡도는 얼마나 많은 파라미터를 학습하느냐에 비례하는데, SHiRA는 0이 아닌 파라미터의 개수가 적기 때문에, Dense 방식보다 훨씬 더 적은 연산과 데이터로 학습이 가능하다.

Lemma 4.2

희소 SHiRA 행렬을, LoRA처럼 저랭크 행렬로 근사했을 때 오차가 얼마나 되나?를 증명

Sparsity 비율을 지정하면, LoRA는 SHiRA의 r-랭크 근사가 되며, 근사 오차는 SHiRA adapter의 $r+1$번째 특이값의 제곱($σ^2_{r+1}$)으로 제한된다.

SHiRA adapter가 $m\times n$의 행렬일 때, 이 행렬을 SVD하면

$\Delta W=U\Sigma V^T$
$\Sigma$ : 특잇값($σ_1,σ_2,...)$

LoRA는 rank r이므로 $\Sigma$의 특잇값에서 $σ_1$~ $σ_r$까지만 써서 근사한다.

Eckart–Young theorem
임의의 행렬을 rank r로 근사할 때, 상위 r개의 특이값만 남기는 것이 가장 좋다.

• 그렇다면, 근사한 값의 오차(Frobenius norm)는 상위 r개의 특이값 이후인 $σ_{r+1}$부터 특이값에 의해 결정된다.

  $Error\leqσ^2_{r+1}$

논문에서 말하는 오차 상한(근사 오차)가 바로 이것으로 SHiRA의 $r+1$번째 특이값의 제곱이 된다.

즉, SHiRA 행렬을 LoRA가 r-rank로 근사할 수 있고, 그 오차가 SHiRA 행렬을 SVD했을 때, $r+1$번째 특이값 제곱에 의해 제한된다.

따라서, 크기가 $m\times n$인 임의의 r랭크 LoRA adapter는, 0이 아닌 원소의 개수가 $r(m\times n)$개인 SHiRA adapter의 근사로 볼 수 있다.

SHiRA = 희소 행렬
LoRA = 희소성은 없지만 랭크 제한된 행렬
LoRA는 SVD를 통한 "압축 버전"이어서 SHiRA를 근사할 수 있음

Lemma 4.3

SHiRA scaling factor는 adapter의 rank와 무관하며, 1로 설정할 수 있다.
(LoRA에서는 rank가 커질수록 $\alpha$를 조정해야 안정적인 학습이 가능하지만 SHiRA는 필요없음)

LoRA의 업데이트 식은 다음과 같다.

$Y_{out}=(W+\alpha_rBA)X_{in}+b$

• $\alpha_r =\frac{\alpha}{r}$ : scaling factor

LoRA에서 $\alpha$를 조정하는 이유는 rank r이 커질수록 $BA$의 값이 커질 수 있어 gradient가 폭발 위험이 있다.
그래서 $\alpha_r =\frac{\alpha}{r}$로 줄여서 안정화 시킨다.

---

하지만, SHiRA의 업데이트 식은 다음과 같다.

$Y_{out}=(W+S)X_{in}+b$

• $S$ : sparse matrix

$S$에서 0이 아닌 위치의 가중치 값은 base 가중치 $W$에서 해당 값으로 초기화 된다
즉, 원래 $W$에서 일부 위치만 학습하는데, 이런 초기화는 fine-tuning시 업데이트가 안정적으로 유지되게 한다.

결과적으로 rank와 무관하게 학습 안정성을 확보하게 된다.

즉, LoRA에서는 $Y_{out}=(W+\alpha_rBA)X_{in}+b$으로, 출력값($Y_{out}$)이 $r$에 비례하기 때문에 r이 크면 scaling이 필요하지만,

SHiRA는 $Y_{out}=(W+S)X_{in}+b$으로, 출력값($Y_{out}$)이 sparse matrix $S$에 의해 결정되기 때문에 rank가 아닌, 0이 아닌 가중치의 개수에 비례하게 된다.

4.2 Adapter Weight Orthogonality in Multi-Adapter Fusion

SHiRA와 LoRA의 adapter 설계가 multi adpater 결합에서 어떤 성질을 갖는지 이론/실험적인 통찰 제공

Lemma 4.4

두 개의 adapter $\Delta W_1, \Delta W_2$가 있을 때, 한 adapter가 다른 adapter의 null space에 속한다면, 두 adapter는 직교하기 때문에 서로 간섭 없이 효율적으로 결합될 수 있음을 의미한다.

$A_1^TA_2=0$

한 adapter가 다른 adapter의 null space에 속한다는 의미로 두 adapter의 sparse 행렬간 내적이 0으로, 완전히 orthogonal하다

비선형 활성화 함수의 멱급수 전개(power series expansion)

ex) $f(x)=a_0+a_1x+a_2x^2+...$이러한 수식을 멱급수라 한다.

이 멱급수 전개는 adapter 가중치 행렬들의 곱이 있는 항들을 포함한다.

그러나 각 adapter가 서로의 null space에 있으므로, adapter 곱을 포함하는 모든 항은 0이 된다.

ex)

입력 $x$에 대해, 두 개의 adapter $\Delta_1, \Delta_2$가 있다고 할 때, forward과정에서 입력이 지나갈 때는 이렇게 전개된다.

$x'=f(x+\Delta W_1x+\Delta W_2x)$

이를 멱급수로 전개해보면

$f(x+\Delta W_1x+\Delta W_2x)=a_0+a_1(x+\Delta W_1x+\Delta W_2x)+a_2(x+\Delta W_1x+\Delta W_2x)^2$

이를 전개하게 되면 $a_1(\Delta W_1\Delta W_2)x$와 같이 고차항에서는 $\Delta W_1, \Delta W_2$의 곱이 포함되게 된다.

결국, 선형 항인 $a_1\Delta W_1x$와 $a_1\Delta W_2x$에서만 각각 $\Delta W_1, \Delta W_2$가 나오게 되며 독립적이게 된다.

• 즉, 여러 adapter를 합쳐도 forward과정에서 결국 각 adapter가 독립적으로 간섭하지 않음이 증명된다.

위 두 증명으로 adapter들은 곱셈적으로 간섭하지 않는다.

---

두 adapter의 orthogonality를 측정하는 지표

1. 어댑터 가중치 직교성 크기 (AWOM, Adapter Weight Orthogonality Magnitude)

$AWOM(A_1,A_2)=||A^T_1A_2||_2$

AWOM은 두 sparse adapter의 가중치 $A_1, A_2\in \R^{n\times m}$에 대해 곱 $A_1^TA_2$의 $l_2$ Normalization으로 정의된다.

AWOM은 $A_1^TA_2$가 영행렬에서 얼마나 멀리 떨어져 있는지를 측정한다.

• 즉, 얼마나 간섭(직교 위반)이 강한가를 수치로 측정한 지표

2. 어댑터 가중치 직교성 비율 (AWOR, Adapter Weight Orthogonality Ratio)

AWOR은 $A_1^TA_2$의 sparse ratio로 정의된다.

$AWOR=1-\frac{||A^T_1A_2||_0}{m^2}$

• $m^2$ : $A_1^TA_2$의 원소 개수
• $||\cdot||_0$ : 0이 아닌 원소의 개수를 세는 $L_0$ Normalization이다.
• $||A^T_1A_2||_0$ : 두 어댑터가 겹쳐서 non-zero 값을 만든 좌표 수

AWOM과 AWOR은 두 어댑터 가중치 간 직교성 정도를 나타내는 척도로 사용할 수 있다.

Lemma 4.5

SHiRA-Struct 어댑터는 매우 희소한(non-overlapping) 마스크 덕분에 서로 다른 어댑터 간 내적 $A_1^TA_2$가 거의 0에 수렴하여, LoRA보다 훨씬 강한 직교성(orthogonality) 을 가진다.

이는 어댑터들이 모델에 추가될 때 표현이 서로 간섭(interference)하지 않고 분리된(disentangled) 표현을 학습할 수 있게 만든다. 따라서 여러 어댑터를 동시에 쓸 때 융합(fusion)이 안정적이며, Dense 또는 희소 LoRA보다 AWOR(직교성 지표) 가 높다.

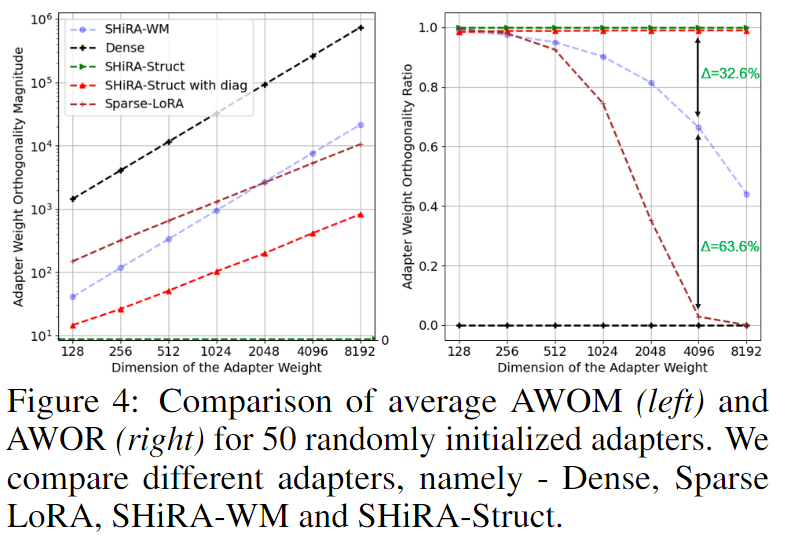
다만, SHiRA-Struct는 rank-1+대각(diagonal) 구조라 개별 어댑터의 표현력은 제한적이어서, 단일 어댑터 성능과 다중 어댑터 융합 간의 트레이드오프가 존재

5. Experiments