FM : Factorization Machines
Factorization Machines
논문이 나올당시 많이 사용했던 SVM 과 MF 같은 Factorization 모델의 장점을 결합한 Factorization Machine을 처음 소개한 논문이다.
등장배경
딥러닝이 등장하기 이전에는 서포트 벡터 머신(SVM)은 커널 공간을 활용하여 비선형 데이터셋에 좋은 성능을 보였기 때문에 가장 많이 사용되는 모델이었다. 그렇지만 추천시스템의 CF환경(user-item interaction)은 매우 sparse한 데이터였기 때문에 SVM이 좋은 성능을 내지 못하고 MF 계열 모델이 더 좋은 성능을 보여왔다.
하지만 MF 계열 모델은 오직 CF 환경에만 적용할 수 있는 단점이 존재 하였기 때문에 context 정보를 반영하지 못했다.
SVM과 MF의 장점을 결합하고자 FM이 등장하였다.
공식
※ CAR 기초 글에서 로지스틱 회귀 수식과 비교 해서 살펴보면 좋다.
- : global bias
- : 변수마다 대응되는 weight
- : 학습 파라미터로 k 차원으로 이루어진 벡터
- : 두 벡터의 스칼라 곱(dot product)으로 을 나타낸다.
수식을 해석해보자.
첫번째 term인 은 일반적인 로지스틱 회귀식으로 볼 수 있는데, 상호작용을 표현하지 않은 각 feature를 학습하는 것을 의미한다.
두번쨰 term이 FM의 핵심인 Factorization Term이다. 와 가 하는 각각의 상호작용을 와 라는 k 차원의 Factorization 파라미터로 표현하여 좀더 일반화 시켰다.
※ Polynomial Model 은 라는 파라미터 하나로 표현한다.
활용
Sparse한 데이터셋에서 예측하기
위의 식을 이용하여 Sparse한 데이터셋에서 예측해보자.
Sparse 데이터셋의 대표격인 MovieLens의 유저 영화 평점 데이터를 생각해보자.
평점 데이터는 일반적인 CF문제의 입력데이터 같이 구성되어 있다.
- 평점데이터 = { (유저1,영화2,5), (유저3,영화1,4), .... }
이 전체유저수를 U, 아이템수를 M이라고 가정하고 평점데이터를 일반적인 입력 데이터로 바꾸게 되면 다음과 같다.
- (유저1,영화2,5) -> [1, 0, 0, ... ,0 0, 1, 0, ... ,0 , 5 ]
파란색 : 유저 / 빨간색 : 영화 / 하얀색 : 평점
이렇게 바꾸게 되면 입력값의 차원이 전체유저와 아이템 수만큼 증가하여 U+M개의 칼럼을 가지지만 해당 id 칼럼 2개를 제외한 모든 칼럼은 0이되며 이는 High Sparsity를 야기하게 된다.
FM에서 가장 중요한 것은 이런 sparse한 데이터의 interaction이 어떻게 학습되는가이다.
다음의 예를 통해 알아보자

유저 A를 기준으로 그림을 설명해보면 다음과 같다.
- 유저A가 본 영화에 대한 데이터는 x1,x2,x3 이다.
- 유저A는 TI, NH, SW를 보았고 각각 5,3,1점의 평점을 매겼다
- 유저A는 영화 ST는 보지 않았다.
이제 유저 A의 ST에 대한 평점을 예측해보자.
A 와 ST의 상호작용을 구하기 위해서는 그림에 나온 데이터들을 가지고 A와 ST의 Factorization 파라미터(, )를 학습해야 한다.
의 경우 유저 B,C 가 평가했음을 알 수 있다. 그리고 유저 B,C 는 SW 라는 영화를 같이 평가했다. 즉 유저 B,C는 영화 SW와 ST를 평가했기 때문에 ST가 SW에 비해서 어떤 특징을 가졌는지를 를 통해 학습할 것이다.
의 경우 유저 A가 평가했으면서 유저 B,C 가 평가한 영화 SW 가 존재한다. 영화 SW는 유저 A,B,C,가 같이 평가했기 때문에 이 데이터를 학습하게 되면 유저 B,C 와는 다른 유저 A의 특징이 에 학습이 될 것이다.
이렇게 유저A와 영화 ST의 실제 상호작용은 없지만 다른 데이터를 통해 각각의 Factorization 파라미터가 학습이 될 것이고 그 파라미터를 통해서 유저 A가 아직 보지않은 영화 ST에 대한 평점이 구해지게 된다.
FM은 이렇게 User-Movie interaction 뿐만 아니라 Movie끼리, Movie-Time 등 각 칼럼끼리의 interaction(Context와의 interaction)이 모두 FM에서 모델링이 된다.
FM의 장점 vs SVM, MF
각각의 모델에 비해서 FM이 어떤 점이 더 좋은지 알아보자.
vs SVM
- SVM은 sparse한 데이터에 대해서 성능이 좋지 못했지만 FM은 sparse한 데이터에 대해서 높은 예측 성능을 보임
- FM은 선형복잡도를 갖기 때문에 수십억개의 학습 데이터에서도 빠르게 학습이 가능
vs MF
- MF는 오로지 CF환경에서만 가능하지만, FM은 CF형태가 아닌 다양한 예측모델에도 활용이 가능한 general한 모델
- id이외에 다른 부가정보들(context 정보)을 모델의 feature로 활용할 수 있음
FFM :Field-aware Factorization Machines
FM의 변형된 모델인 FFM을 제안하여 더 높은 성능을 보인 논문
개요
등장배경
FM은 다양항 예측 문제에 적용가능한 general 한 모델로 특히 sparse한 데이터로 구성된 CTP 예측에서 좋은 성능을 보였다. FFM은 이러한 FM을 PITF(Pairwise Interaction Tensor FActorization) 모델에서 아이디어를 얻어 발전시킨 모델이다.
PITF는 MF를 발전시킨 모델인데 용어 그대로 2차원 Matrix가 아닌 3차원 Tensor로 MF를 확장시키는 모델이다. 하나의 임베딩 만으로는 서로 다른 필드와의 상호작용을 표현하기에 부족했기 때문에 곱해지는 반대편의 필드가 무엇인지에 따라서 다른 임베딩을 사용한 것이다.
PITF는 (user,item,tag) 3개의 필드에 대한 클릭률을 예측하기 위해 (user,item), (item,tag), (user,tag) 각각에 대해서 서로 다른 Latent Factor(Embedding)를 정의하여 구한다.
이렇게 각각에 서로 다른 Latent Factor를 구하는 아이디어를 일반화 하여서 여러개의 필드에 대해서 Latent Factor를 정의 한 것이 FFM이다.
이를 통해 FFM은 사용자가 정의하는 개수만큼 필드를 늘려서 상호작용을 임베딩 시킬 수 있게 된다.
FFM 특징
기존의 FM은 하나의 변수에 대해서 K개로 Factorize 했지만(), FFM은 f개의 필드에 대해 각각 K개로 Factorize 하여 필드별로 서로 다른 latent factor를 가지도록 한다.
이때 Field란 모델을 설계할 때 함께 정의되는 것으로 같은 의미를 갖는 변수들의 집합으로 설정한다.(모델이 정하는 것이 아니라 사용자가 직접 설계해야한다)
Field 예시 )
- 유저 : 성별, 디바이스 , 운영체제
- 아이템 : 광고, 카테고리
- 컨텍스트 : 어플리케이션 , 배너
CTR 예측에 사용되는 feature는 이보다 훨씬 다양한데, 보통 feature의 개수만큼 필드를 정의하여 사용하곤 한다.
공식
FFM의 Fomula는 다음과 같다.
FM에서 바뀐 것은 두번째 factorization term 에서 가 로 바뀐 것 뿐이다.
FM일 경우 두개의 변수가 interation할때 각각에 해당하는 k차원의 벡터()가 내적이 되는 형태로 interaction을 표현하였는데, FFM은 단순히 에 해당하는 가 아니라 로 가 포함되어 있다. 이때 는 의 의미는 반대편인 에 곱해지는 field에 해당하는 factorization 파라미터를 사용한다는 것이다. 그래서 하나의 변수는 총 개의 field를 갖고 각 field별로 factorization 파라미터를 정의 한다는 것이다.
수식이 복잡하니 FM과 비교하여 이해해 보자
vs FM
광고 클릭 데이터가 존재하고 사용할 수 있는 feature가 총 3개(Publisher, Advertiser, Gender) 인 상황을 가정해보자.
| Clicked | Publisher(P) | Advertiser(A) | Gender(G) |
|---|---|---|---|
| Yes | ESPN | Nike | Male |
각 feture에 대해서 표와 같이 정의된 데이터 1개가 있다고 할 때 FM과 FFM을 수식적으로 비교하보면 아래와 같다.
FM의 경우에는 필드가 존재하지 않기 떄문에 하나의 변수에 대해 하나의 factorization 차원()만큼의 파라미터를 학습한다. 은 1차항이고, 그 뒤는 factorization term이다.factorization term은 각각에 변수에 해당하는 factorization 파라미터들이 내적으로 곱해지는 형태이다.
FFM의 경우 각각의 feature를 필드 P,A,G로 정의 하였다. 하나의 변수에 대해서 필드개수()와 factorization 차원()의 곱()만큼의 파라미터를 학습한다.
1차항은 FM과 동일하지만 뒤에 factorization term에는 차이가 있는데 부분이 어떤 것을 의미하는지 알아보자.
- : ESPN 반대편에 곱해지는 것이 A 필드 이므로 ESPN 변수면서 Advertise 필드와 곱해진다는 의미이다. 즉 와 곱해진다.
- : Nike 반대편에 곱해지는 것이 P이므로 과 대응되게 된다.
이처럼 interaction이 일어나는 반대편 변수의 field를 고려하여 factorization 하기 때문에 Field-aware이라는 수식어가 붙은 것을 알 수 있다.
활용
FFM의 필드 구성
CTR 문제 데이터의 대부분은 Categorical Feature라고 언급한 바 있다. 우선 Categorical Feature일때 FFM의 필드가 어떻게 구성되는지 위의 예시를 통해 FM과 비교 하여 보자.
FM
| Label | feature1 | feauture2 | ... |
|---|---|---|---|
| Yes | P-ESPN | A-Nike | G-Male |
| Yes | 1 | 1 | 1 |
FFM
| Label | field1 : feature1 | field2 : feauture2 | ... |
|---|---|---|---|
| Yes | P: P-ESPN | A:A-Nike | G:F-Male |
| Yes | 1 | 1 | 1 |
성능 비교
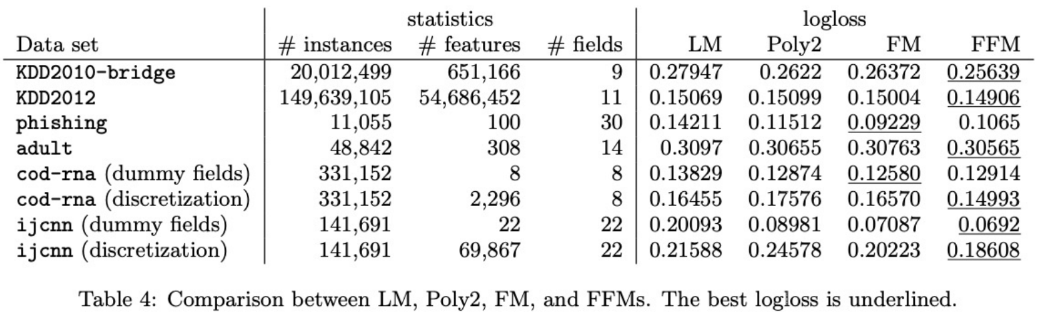
앞선 두 모델보다 로지스틱회귀나 Polynomial model 보다 FM과 FFM이 좋은 성능을 보인 것을 알 수 있고,
어떤 데이터 셋에 대해서는 FM이 FFM보다 더 좋은 것을 볼 수 있는데 이는 field를 사용하여 명시적으로 feature를 구분하는 것이 도움이 되지 않았을수도 있어 overfitting이나 underfitting이 일어날 수 있음을 암시한다(학습 파라미터수가 증가하기 때문에).
