[ML] Advice for Applying Machine Learning

machine learning을 실생활에서 적용하는 것은 쉬운 것이 아니다. 이번 시간에는 실생활에서 machine learning을 적용하는 best practice를 알아보고, learned models의 성능을 평가하는 가장 좋은 방법에 대해 알아보자.

Evaluating a Learning Algorithm

Deciding What to Try Next

machine learning system을 개발하거나 machine learning system의 performance를 개선해야한다고 가정하자. 그때 어떻게 좋은 방안을 결정할 수 있을까?

이것을 설명하기 위해서, housing price를 예측하기 위해 regularized linear regression을 구현한다고 가정하자. 그 때 cost function은 다음과 같다.

하지만, 새로운 set에 이 hypothesis를 테스트해보니 predictions에 에러가 너무 컸다. 이를 해결하기 위해선 어떻게 해야할까?

1. 더 많은 training examples를 모은다.
   하지만 데이터를 아주 많이 모으는데는 너무 많은 노력이 필요하고, 한계가 반드시 있다.
2. feature의 갯수를 줄인다.
   overfitting을 줄이기 위해서 feature의 갯수를 줄일 수 있다.
3. 추가적인 feature을 만들 수 있다.
4. polynomial feature들을 추가할 수 있다. ($x_1^2,x_2^2,x_1x_2,etc.$)
5. regualarization parameter $\lambda$를 decresing하거나 increasing할 수 있다.

하지만 이 방법들을 주먹구구식으로 시도하기보단, 현재 알고리즘의 어느 부분에서 문제가 있는지 진단(Diagnostic)해서 체계적으로 알고리즘을 개선하는 편이 훨씬 효율적일 것이다.

Diagnostic은 구현하는데 시간이 좀 걸리지만, 나중에 또 다른 방안(avenue)를 찾을 필요가 없으므로 더 효과적이다.

Evaluating a Hypothesis

어떻게 overfitting 문제와 underfitting 문제를 막을 수 있는지 살펴보자.

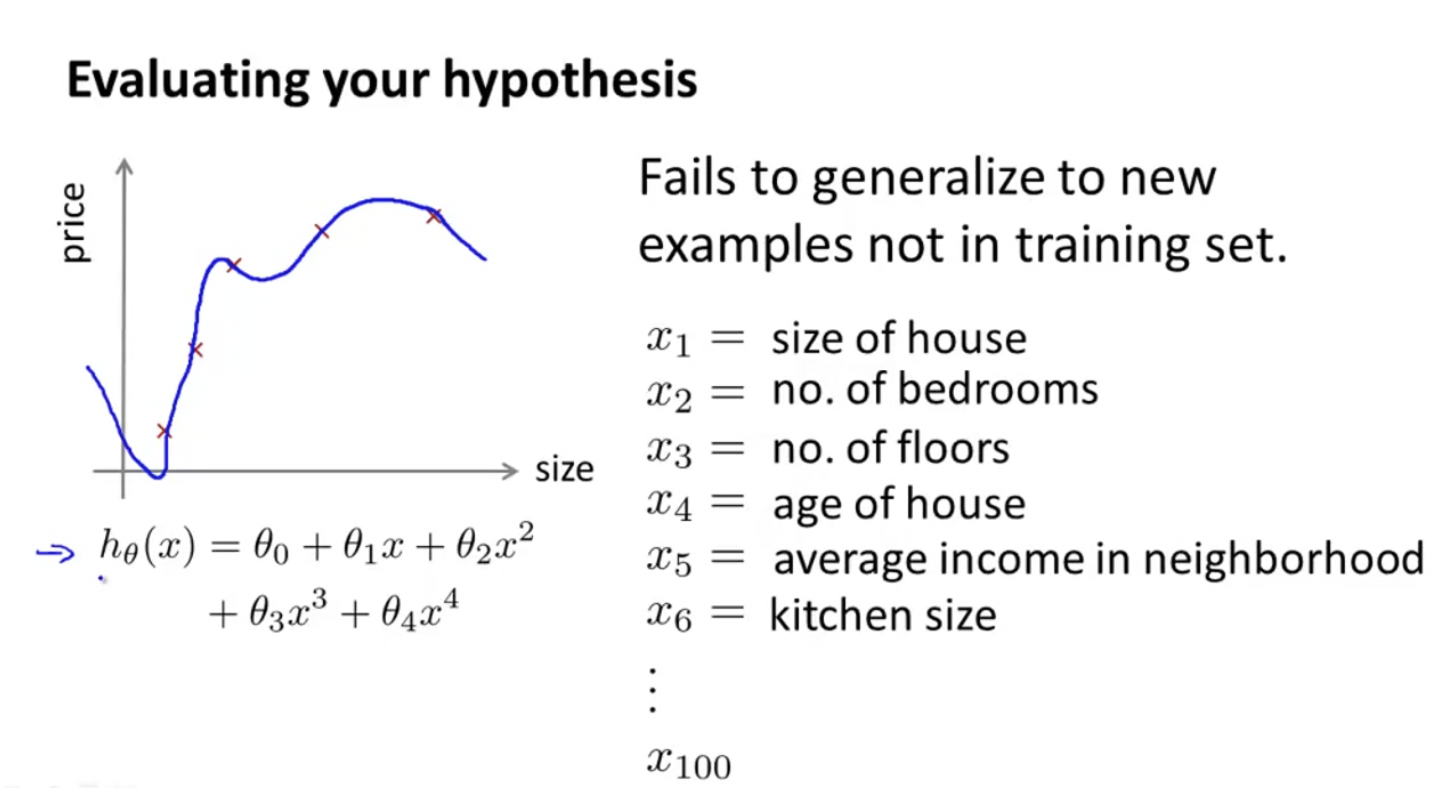
이렇게 hypothesis를 4차 다항식으로 나타내면, overfitting이 나타나는 것을 확인할 수 있다. 이렇게 feature의 갯수가 많으면 그래프를 통해 시각적으로 표현하기 어렵기 때문에, 우리의 hypothesis를 평가할 다른 방법을 찾아봐야 한다.

가장 기본적인 방법은 다음과 같다. 우리가 다음과 같은 데이터셋을 갖는다고 가정하자.

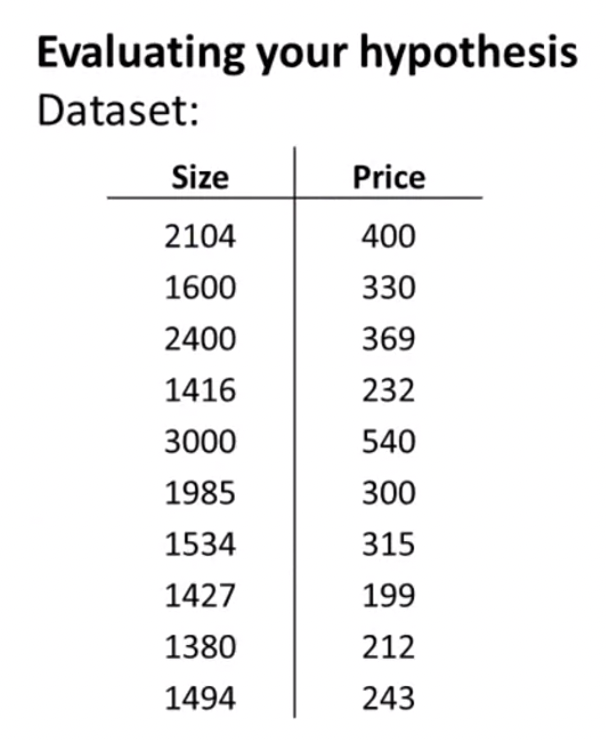
10개의 training examples이 있다. 이 training examples을 랜덤하게 섞어서 두 부분으로 나눈다. 70% 정도로 나눈 첫 부분을 training set, 30% 정도로 나눈 나머지 부분을 test set으로 나눈다.

$m_{test}=number.\;of\;test\;example$이라고 하자. $(x_{test}^{(i)},y_{test}^{(i)})$는 하나의 test example을 가리킨다. 만약 $(x_{test}^{(1)},y_{test}^{(1)})$ 이면, 각각 1427, 199를 가리킨다.

이제 어떻게 linear regression에서 train/test하는지 알아보자.

1. training data로부터 parameter $\theta$를 학습한다. 이로인해 training error $J(\theta)$를 최소화할 수 있다.
2. test data로부터 test error $J(\theta)$를 계산한다. 여기서 $\theta$는 training data에서 알아낸 parameter $\theta$를 사용한다. test error $J(\theta)$는 다음과 같이 계산한다.

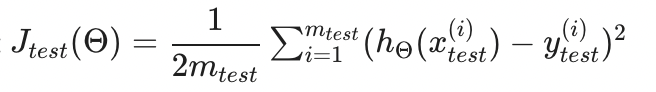
그럼 classification logistic regression에서 train/test하면 어떻게 될까? linear regression한 것과 비슷하다!

1. training data로부터 parameter $\theta$를 학습한다. 이로인해 training error $J(\theta)$를 최소화할 수 있다.
2. test data로부터 test error $J(\theta)$를 계산한다. 여기서 $\theta$는 training data에서 알아낸 parameter $\theta$를 사용한다. 단, test error $J(\theta)$를 구하는 방법이 linear regression과 다르다.
3. 때때로 또 다른 대안이 있는데, 이를 misclassification error 또는 0/1(zero one) misclassification error라고 부른다.

위 식의 조건을 보면, 왜 $err(h_\theta(x),y)$가 1, 0인지 파악할 수 있다. 이를 이용해서,

이렇게 test error을 정의할 수 있다.

Model Selection and Train/Validation/Test Sets

다음과 같은 상황이 있다고 가정하자. Data set에 잘 맞는 polynomial 차원 수를 결정해야 한다. 이것을 model selection이라고 한다. 우리는 단순히 data를 train set과 test set으로 쪼개는 것을 배우는 게 아닌, 어떻게 데이터를 train, validation, test sets으로 바꾸는 지에 대해 배우려고 한다.

우리는 이미 overfitting의 문제에 대해 살펴봤다. overfitting은 learning algorithm이 training set에 잘 맞기 때문에 일어났고, training set에 잘 맞지만 이런 경우는 좋은 hypothesis라고 할 수 없었다.

model selection problem을 생각해보자. 다음과 같은 상황에서 data에 잘 맞는 polynomial degree를 찾는다고 해보자. linear function부터 10차다항식까지 다양하다. d=degree of polynomial이라고 하면 각 함수는 $d=i$라고 나타낼 수 있고, 각 함수의 $\theta$ 값들을 원소로 갖는 벡터 $\Theta$가 있다고 가정하면, $\Theta^{(i)}$라고 할 수 있다. 이를 $\theta$로 test set error $J_{test}(\theta^{(i)})$를 만들어서 test set의 퍼포먼스를 측정할 수 있다. 아래와 같이 말이다.

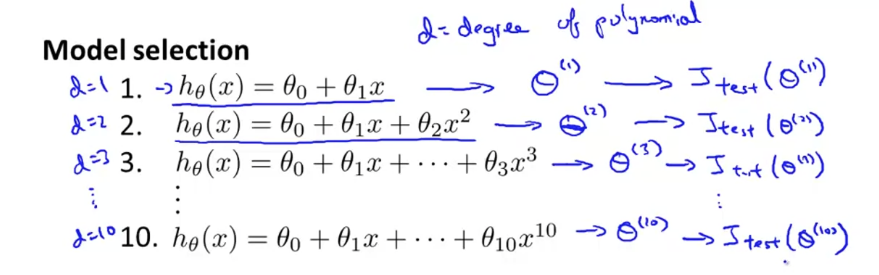
이제, 이 모델들 중 하나를 선택하기 위해서, 어떤 모델이 가장 낮은 test set error을 가지고 있는지 확인할 것이다.

$J_{test}(\theta^{(5)})$일 때의 test error가 가장 작아서, $\theta_0+...+\theta_5x^5$를 선택했다고 하자. 이 model은 과연 잘 일반화되었을까? $J_{test}(\theta^{(5)})$는 generalization error의 optimistic estimate일 확률이 높다. 왜냐하면, 우리의 extra parameter $d$는 Test set에 맞춰진 것이기 때문이다. parameter $d$를 test set에 맞췄으므로, test set에 대한 hypothesis의 퍼포먼스를 잘 평가할 수 없다.
이 문제를 해결하기 위해서, 다음과 같이 주어진 data set에서 training set과 test set으로 나누는 것 대신, training set, (cross)validation set, test set 이렇게 세가지로 나눈다. 세 가지의 set은 다음과 같은 비율로 나눈다.

• Training set : 60%
• Cross validation set : 20%
• Test set : 20%

각 set에서의 error는 다음과 같이 정의한다.

Training Error

$J_{train}(\theta)=\frac{1}{2m}\sum\limits_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]^2$

Cross-validation error

$J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum\limits_{i=1}^{m_{cv}}[h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv}]^2$

Test Error

$J_{test}(\theta)=\frac{1}{2m_{test}}\sum\limits_{i=1}^{m}[h_\theta(x^{(i)}_{test})-y^{(i)}_{test}]^2$

이를 이용해서 Model Selection은 다음과 같이 진행한다.
다음과 같은 모델이 있다.

Model Selection
1. 먼저 $J(\theta)$를 최소화하는 $\theta$들을 원소로 갖는 벡터 $\Theta^{(i)}$들을 최적화한다.
2. $J_{cv}(\theta)$를 이용해서 polynomial degree $d$를 찾아낸다.
3. $J_{test}(\Theta^{(d)})$를 이용해서 generalization error을 추정한다.

Bias vs. Variance

learning algorithm을 작동시켰을 때, 만약 생각했던 대로 작동하지 않는다면 high bias problem이나 high variance problem을 가지고 있기 때문일 수 있다. 다시 말해, underfitting problem이나 overfitting problem을 가지고 있다는 것이다. 이런 경우, 두 문제가 bias인지, variance인지를 알아내는 것은 algrithm을 향상시키는데 굉장히 강력한 indicator를 준다. 따라서 이번에는 bias와 variance issue에 대해 더 깊게 파헤치고(delve), 더 잘 이해해보는 시간을 가질 것이다.

Diagnosing Bias vs. Variance

우리는 위와 같은 hypothesis를 자주 봤다.
또, 우리는 앞서 다음과 같이 training error와 cross validation error을 정의했다.

Training Error

$J_{train}(\theta)=\frac{1}{2m}\sum\limits_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]^2$

Cross-validation error

$J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum\limits_{i=1}^{m_{cv}}[h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv}]^2$

이 식들을 이해하기 위해 x축은 polynomial degree $d$이고, y축은 error인 plane에 플롯팅을 해보자.
Training Error은 $d$가 작을 수록(hypothesis의 차수가 낮을 수록) error가 클 것이고, $d$가 클수록(hypothesis의 차수가 클수록) error가 작을 것이다.

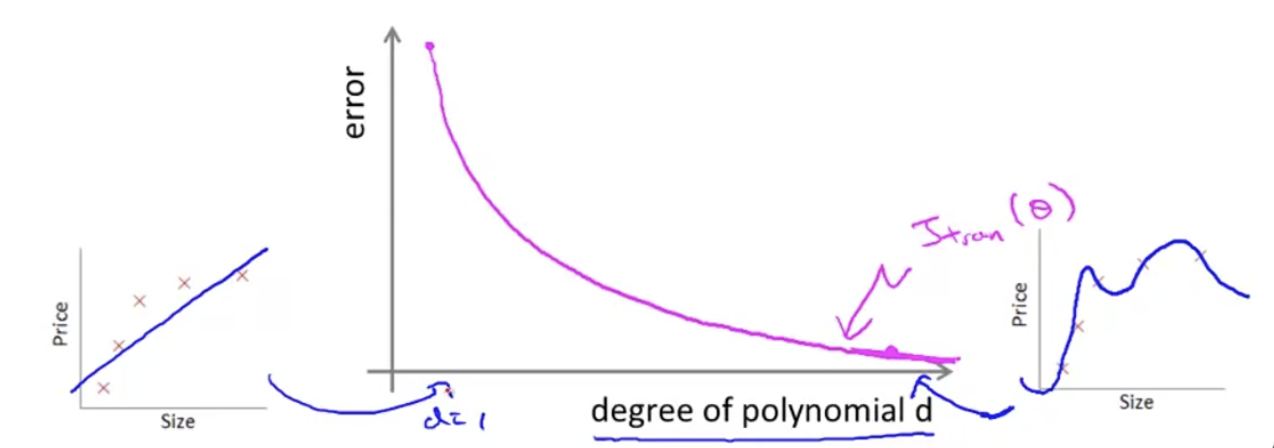
Cross Validation error은 Test Error와 비슷한 결과값을 낸다. 만약 $d$가 작으면, underfitting error가 생기기 때문에 error는 크다. 중간값의 $d$라면, error는 줄어들 것이고, $d$가 커지면 overfitting이 생기기 때문에 다시 error는 늘어날 것이다.

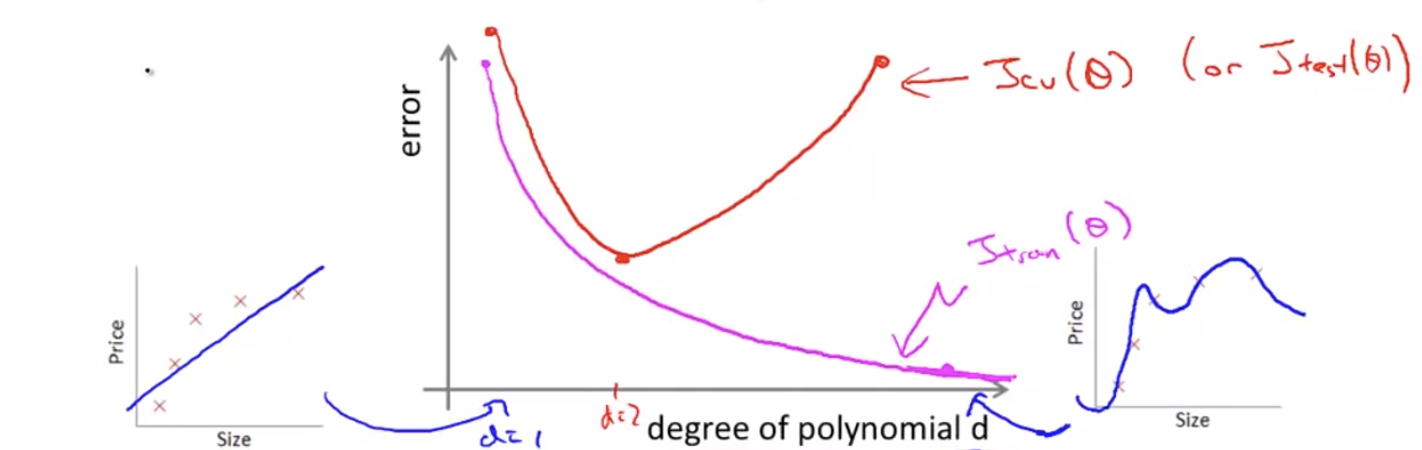
다시 처음 질문을 던져보자. 만약 나의 learning algorithm이 생각했던 것만큼 성능이 나오지 않았을 때($J_{cv}(\theta)$ 또는 $J_{test}(\theta)$가 높을 때), 이것은 bias problem일까, variance problem일까?

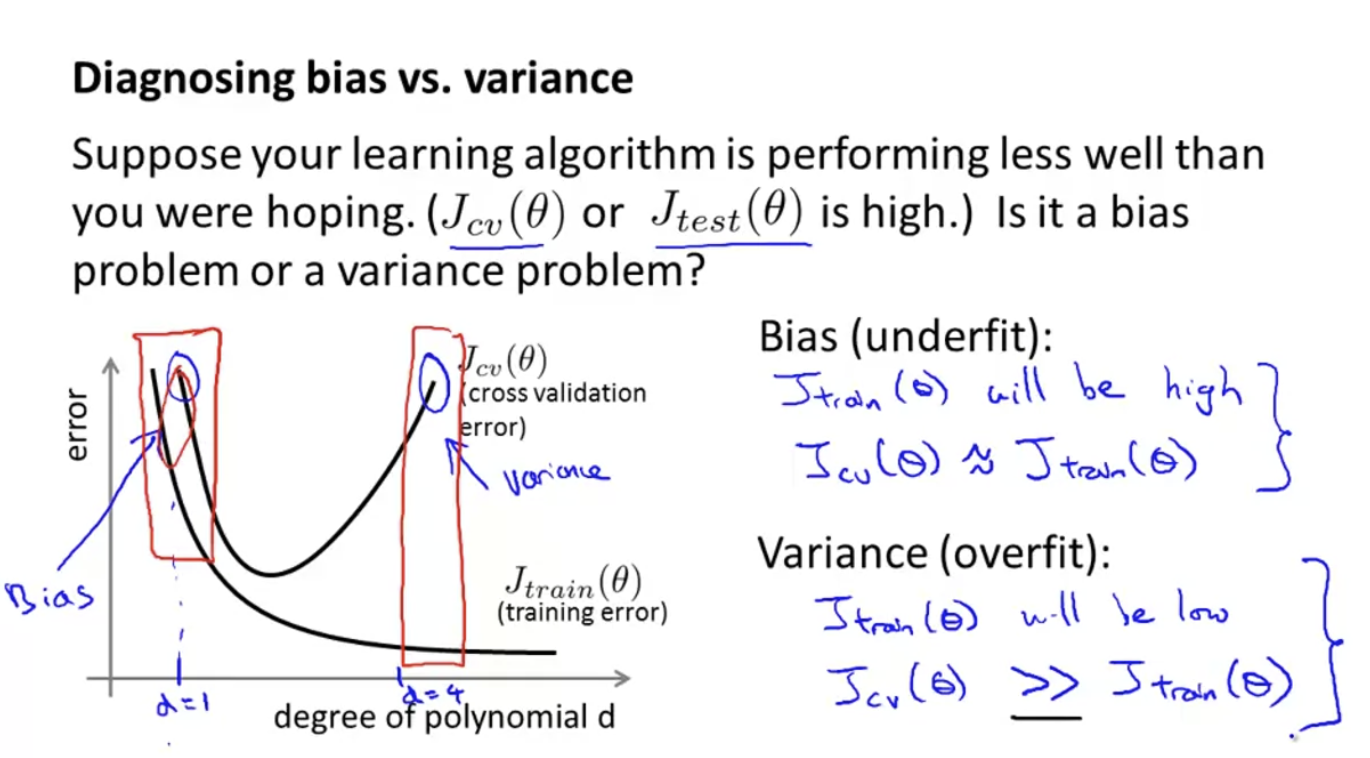
bias problem이면 underfitting 문제가 발생한다. 이땐 $J_{train}(\theta)$이 높고, $J_{cv}(\theta)≈J_{train}(\theta)$ 이다.
variance problem이면 overfitting 문제가 발생한다. 이땐 $J_{train}(\theta)$이 낮고, $J_{cv}(\theta)>>J_{train}(\theta)$임을 확인할 수 있다.

Regularization and Bias/Variance

우리는 앞서 regularization이 overfitting을 예방하는 것을 확인할 수 있었다. 하지만 어떻게 이것이 bias와 variances에 영향을 미칠 수 있을까? 이번 시간에는 bias와 variance 문제에 대해 더 깊게 이야기 해보고, 어떻게 regularization에 의해 영향을 받는지 알아보도록 하겠다.

다음과 같이 high auto polynomial를 fitting했다고 가정하자. overfitting을 막기 위해, regularization도 사용하려고 한다.$\lambda$를 포함한 두번째 항이 model의 bias와 variance사이의 균형을 조절한다.

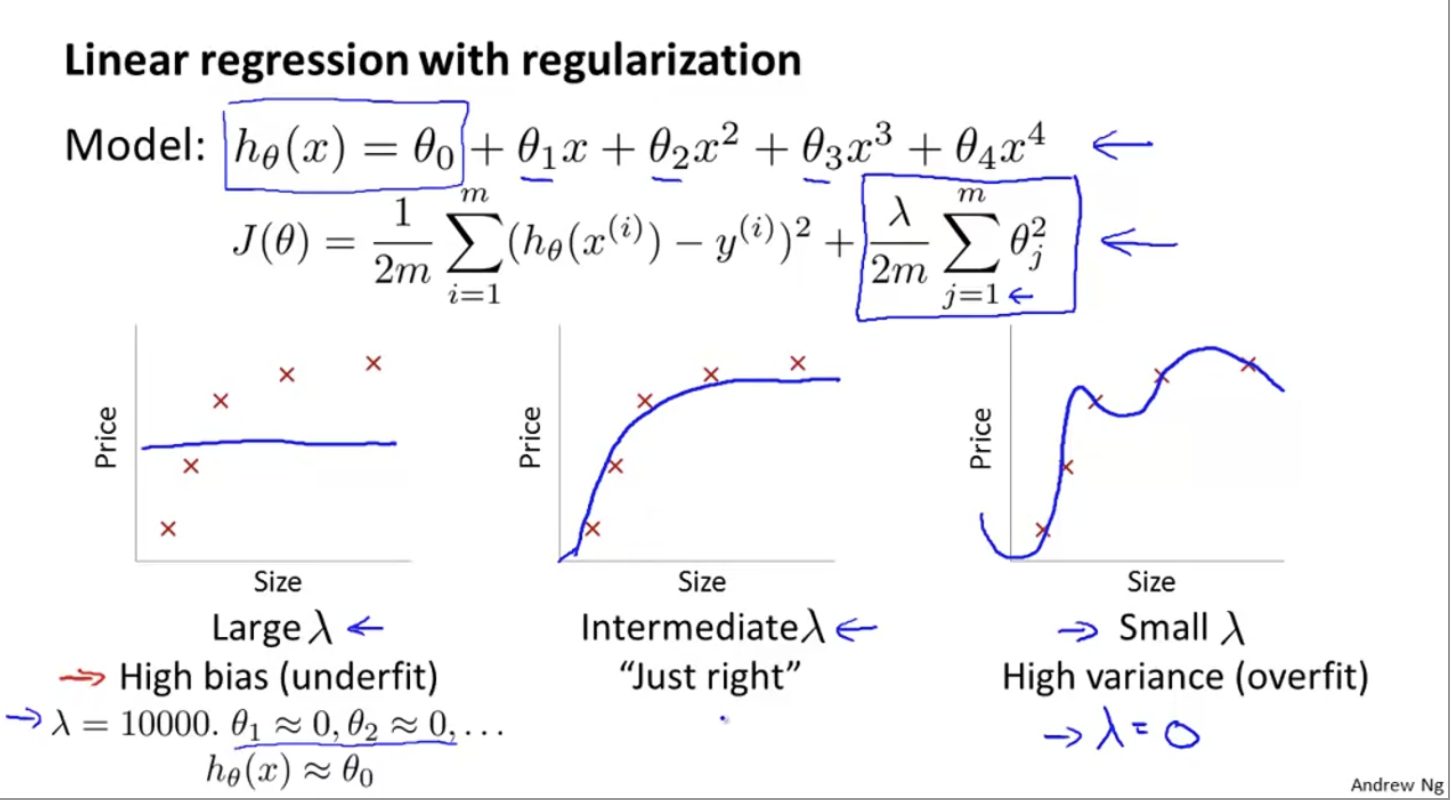
$\lambda$값에 따라서 다음과 같이 hypothesis를 만들어낼 수 있다. 그럼 어떻게 자동으로 좋은 regularization parameter $\lambda$를 고를 수 있을까?

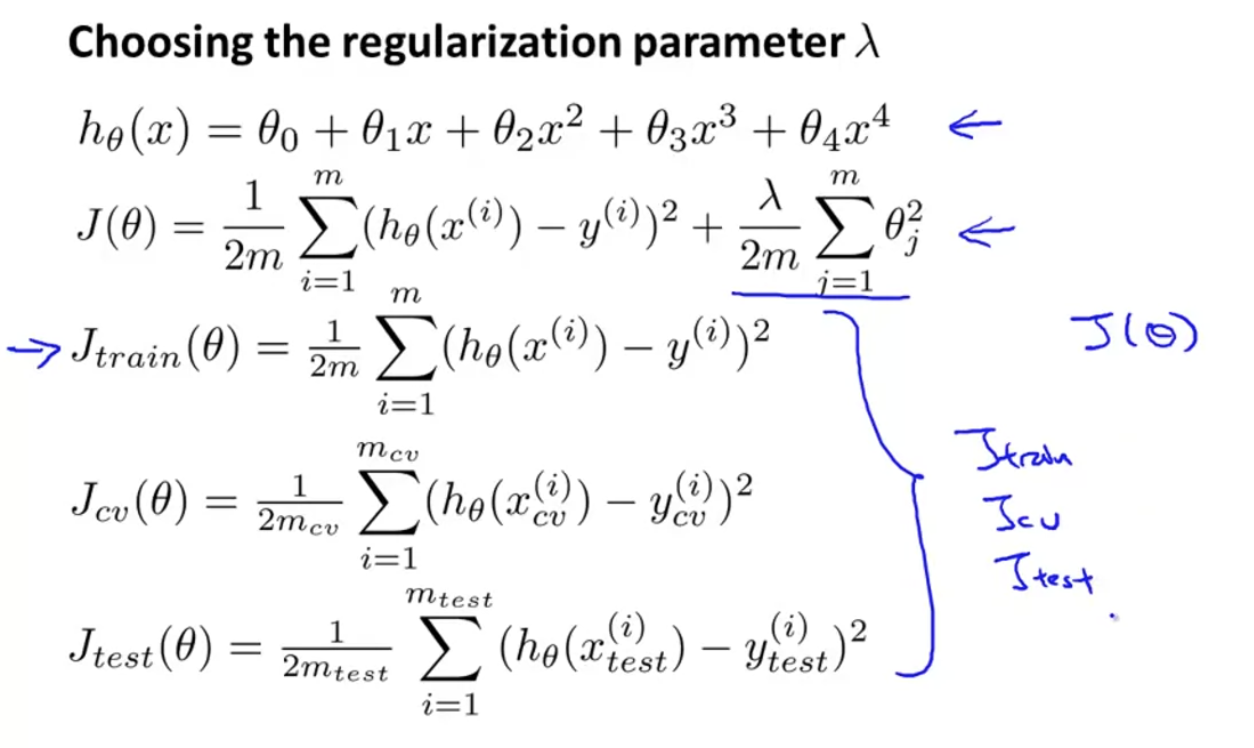
우리의 model은 $h_{\theta}(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4$이고,
learning alogirhtm objective는 $J(\theta)=\frac{1}{2m}[{\sum\limits_{i=1}^m}(h_{\theta}(x^{(i)}) - y^{(i)})^2+\lambda{\sum\limits_{j=1}^m}\theta_j^2]$ 이다.
regularization을 사용하기 위해서, $J_{train}(\theta),J_{cv}(\theta),J_{test}(\theta)$를 셋팅하되, extra regularization term 없이 좀 다르게 define하도록 하겠다(이게 뭔 뜻이지,, 앞에서 정의한 거랑 똑같은데..).
$J_{train}(\theta)=\frac{1}{2m}\sum\limits_{i=1}^{m}[h_\theta(x^{(i)})-y^{(i)}]^2$
$J_{cv}(\theta)=\frac{1}{2m_{cv}}\sum\limits_{i=1}^{m_{cv}}[h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv}]^2$
$J_{test}(\theta)=\frac{1}{2m_{test}}\sum\limits_{i=1}^{m}[h_\theta(x^{(i)}_{test})-y^{(i)}_{test}]^2$
$\\$
아래와 같이 다양한 람다를 가지고 있다고 하자.

각 $\lambda$를 선택해서 $J(\theta)$를 최소화하는 $\theta$를 알아내서, 그 theta들의 벡터를 $\Theta^{(i)}$라고 하자. 이를 모든 lambda에 대해서 하면, $\Theta^{(1)},\Theta^{(2)},\Theta^{(3)},...,\Theta^{(12)}$를 얻을 수 있다. 그리고 모든 람다에 대해, cross validation set을 이용해 cross valiadation error $J_{cv}(\Theta^{(i)})$를 구해서, 가장 작은 $J_{cv}(\Theta^{(i)})$를 가지는 것을 선택한다.
이번 예시에선 5번째 polynomial이 가장 작은 validation error을 가진다고 하자. 그럼 test error는 $J_{test}(\Theta^{(5)})$가 된다.

regularization parameter $\lambda$에 따른 bias와 variance를 살펴보자. $\lambda$가 크면 underfitting(bias problem)이 일어나고, $\lambda$가 작으면 overfitting(variance problem)이 일어날 것이다.

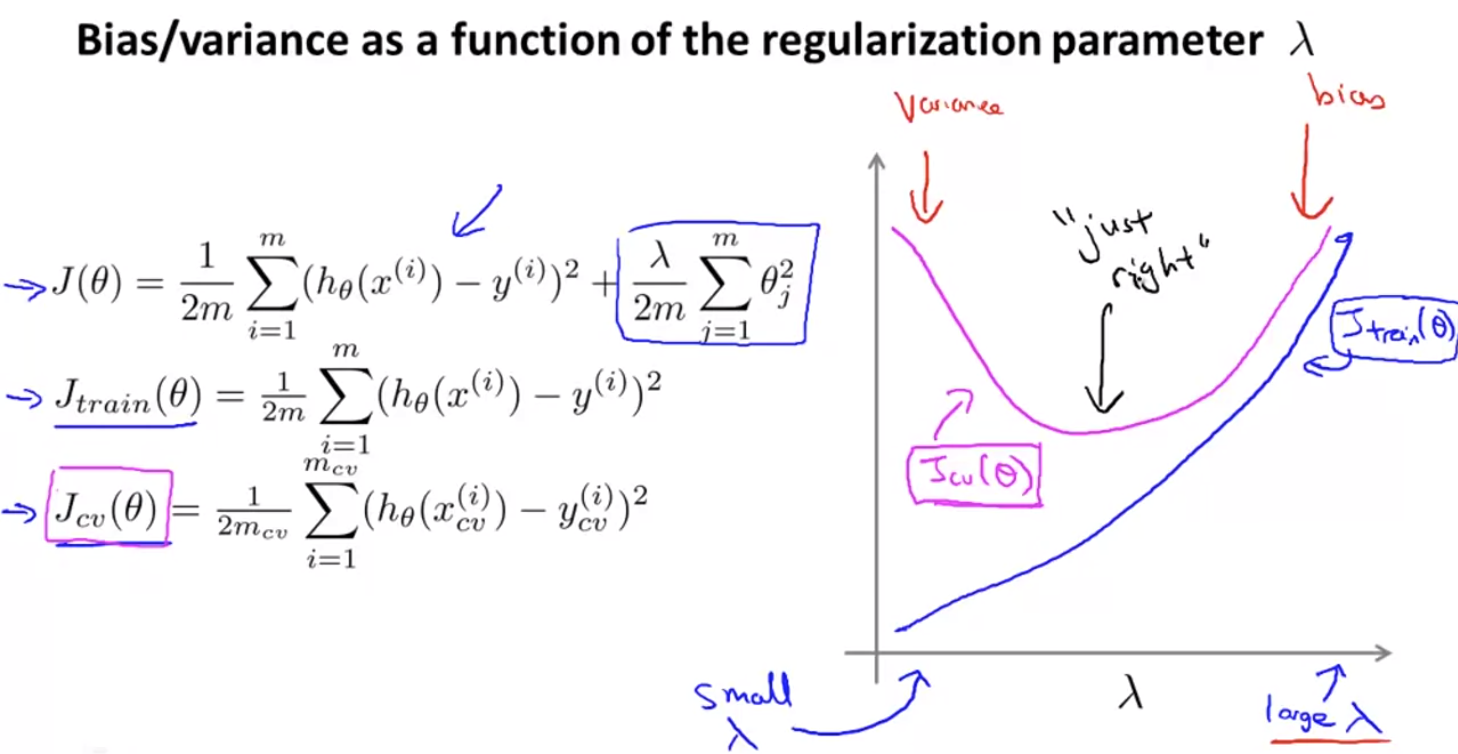
위는 $\lambda$에 대한 $J_{train}(\theta)$,$J_{cv}(\theta)$를 나타낸 것이다. $\lambda$가 너무 크지도, 작지도 않으면 just right이다.
이 그래프를 통해 적절한 $\lambda$를 찾아낼 수 있다.

Learning Curves

만약 algorithm이 잘 작동하고 있는지 확인하고 싶거나, algorithm의 퍼포먼스를 향상시키고 싶다면, Learning Curves는 plottnig할 때 아주 실용적이다. Learning Curve는 physical learning algorithm이 bias나 variance problem으로 성능이 떨어지고 있는지 진단할 때 자주 사용된다.

Learning Curve는 Training example 갯수에 따라 error($J_{train}(\theta),\;J_{cv}(\theta)$)를 그래프로 나타낸 것이다. 이 Learning curve를 통해 underfitting, overfitting을 진단할 수 있다.

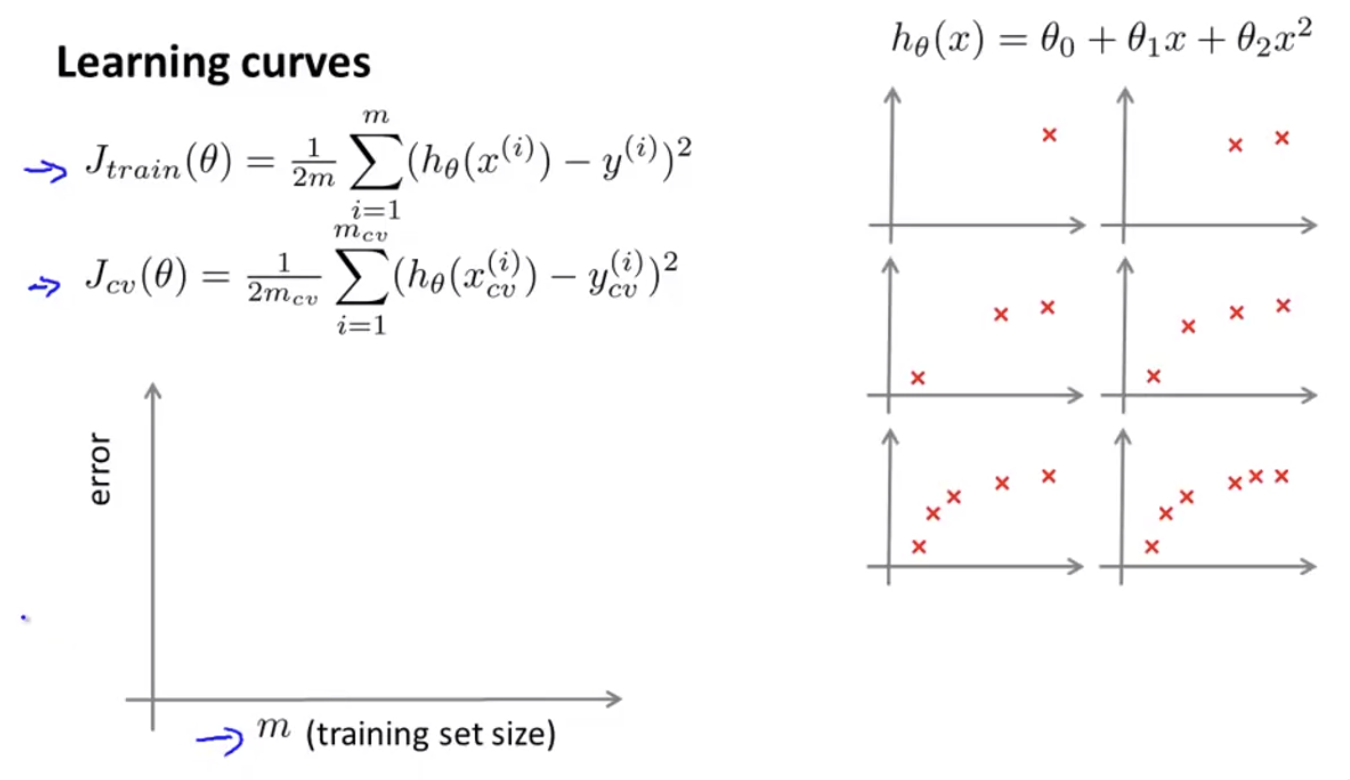
오른쪽을 보면 model $h_{\theta}(x)$이 2차 다항식임을 확인할 수 있고, 그 아래 training set이 왼쪽 위부터 한 개, 두 개, 세 개, 네 개, 다섯 개, 여섯 개 있는 것을 확인할 수 있다. 각각의 training set에 대하여 hypothesis function을 그려보면 다음과 같다.

$m=1,2,3$ 이면 $J_{train}(\theta)≈0$일 것이다. training set에 꼭 맞는 hypothesis를 그릴 수 있기 때문이다. 따라서 training set이 작으면 error도 작아질 것이다. 아래와 같이 말이다.

하지만 training set이 점점 많아지면, error가 증가할 것이기 때문에, 그래프는 다음과 같아진다.

cross validation error는 만약 아주 작은 training set이 있다면 generalization을 하기 힘들기 때문에 error가 클 것이고, 많은 training set이 있다면 error는 줄어들 것이다. 그럼 다음과 같은 Learning curve를 만들 수 있게 된다.

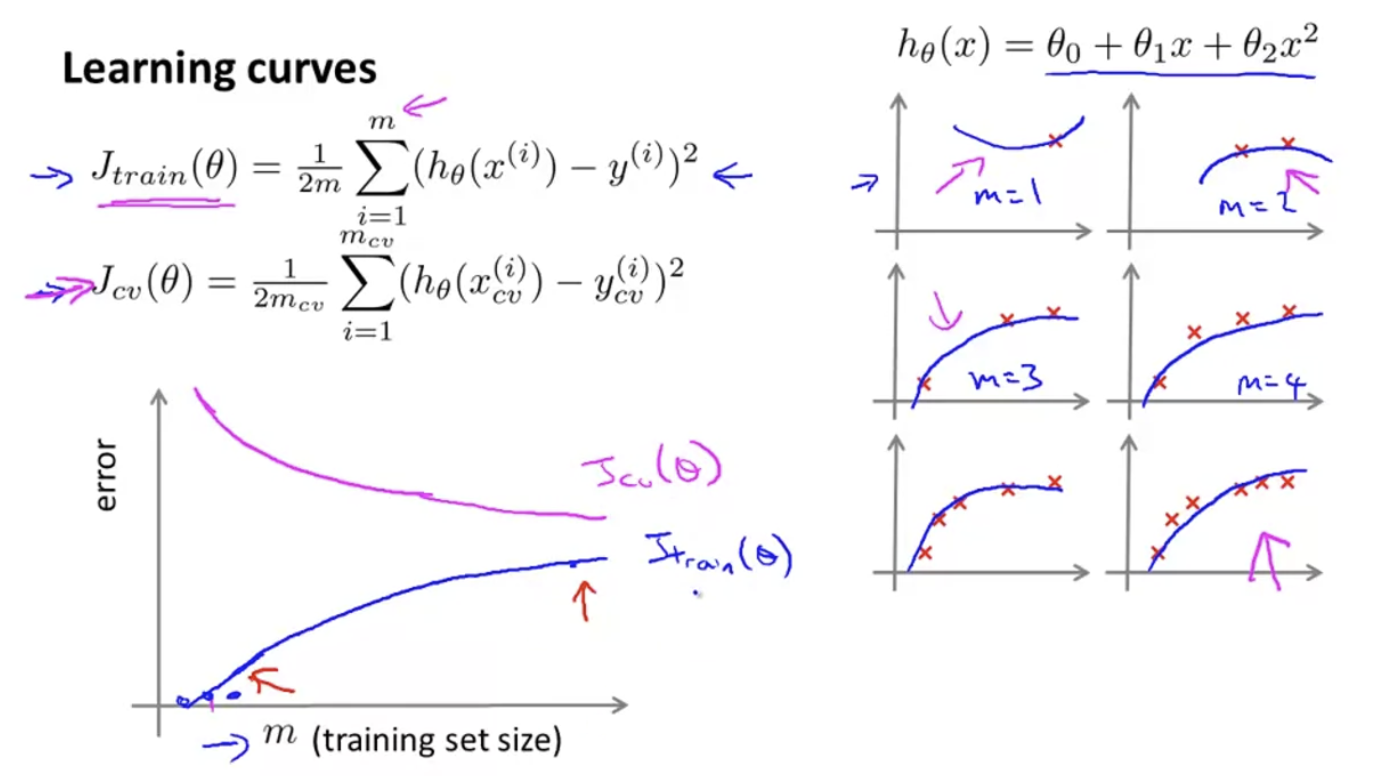
High Bias일 때의 Learning Curves를 살펴보자.

training error와 cv error가 모두 큰 모습을 확인할 수 있다. 또, high bias에선 training data를 많이 추가해줘도 좋은 효과를 얻기가 힘들다.

High Variance일 때의 Learning Curves를 살펴보자.

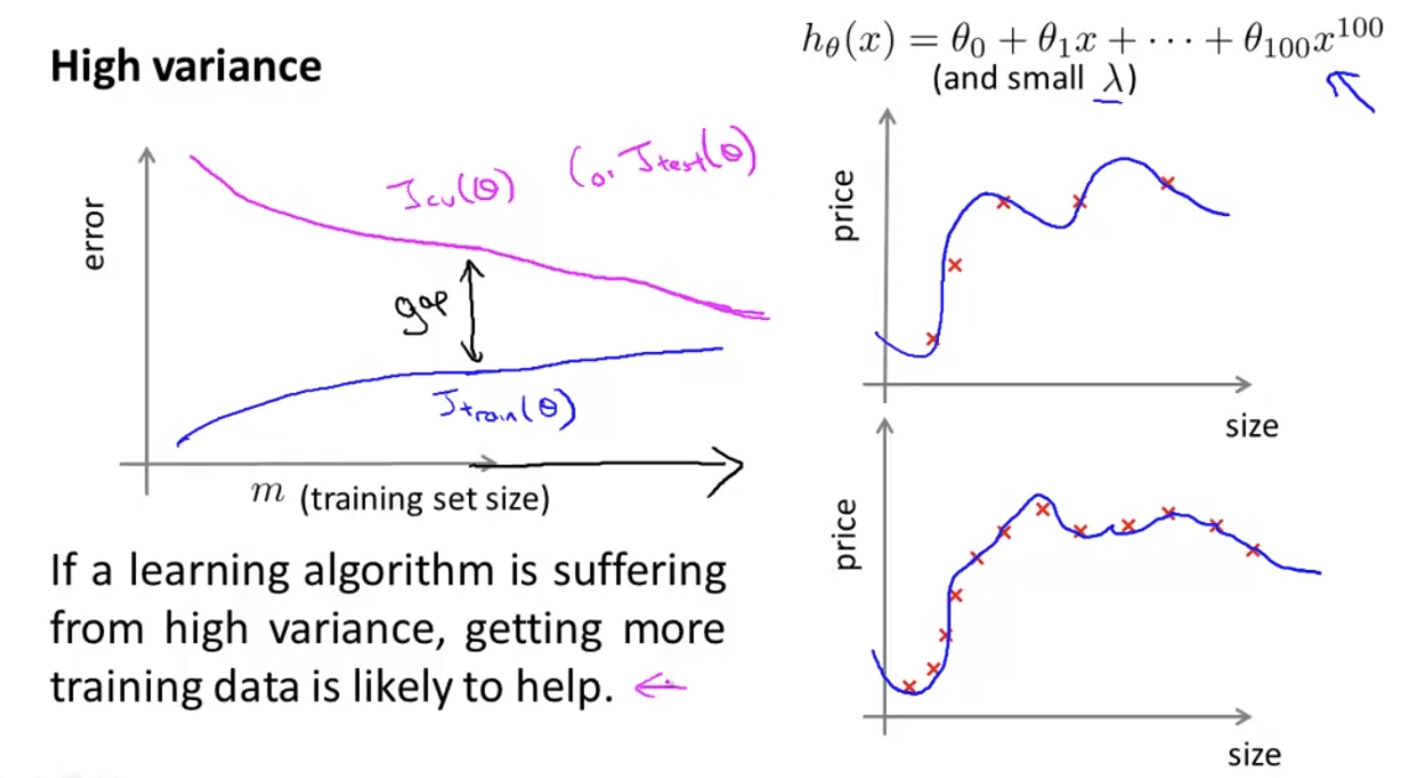
High Variance에선 training error와 cv error 의 gap이 있다. high variance의 문제가 있을 땐, training data를 늘리는 것이 도움이 될 수 있다.

Deciding what to try next(revisited)

우리는 지금까지 learning algorithm 평가방법과 model selection, bias/variance에 대해서 이야기를 나누었다. 이제 이것들이 어떻게 도움을 줄 수 있는지 살펴보자.

앞서 Housing price를 예측하는 regularized linear regression이 새로운 데이터에 대해 generalize하지 못한다면, 어떤 방법을 쓸 건지 이야기를 나눴었다. 방법은 다음과 같았다.

• Get more training examples → fix high variance
• Try Smaller sets of featrues → fix high variance
• Try getting additional features → fix high bias
• Try adding polynomial features($x_1^2,x_2^2,x_1x_2,etc.$) → fix high bias
• Try decreasing $\lambda$ → fix high bias
• Try increasing $\lambda$ → fix high variance

---

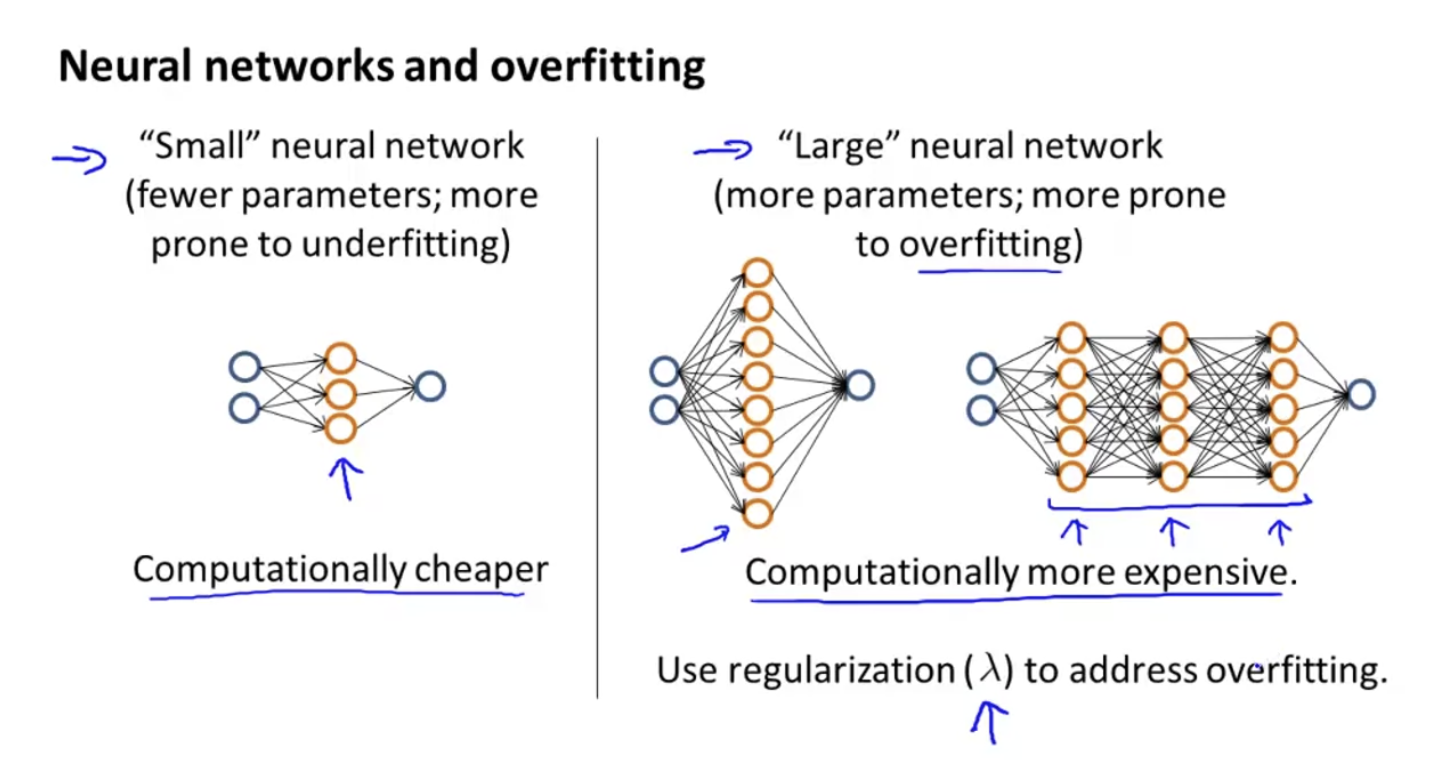
Neural network는 하나의 hidden layer을 가진 Network(small neural network)와 여러개의 hidden layer을 가진 network(large neural network)로 분류할 수 있다. 각각의 특징은 아래 사진과 같다.