[ML] Neural Networks : Learning

Minjeong Park·2021년 8월 20일

Machine Learning

목록 보기

14/17

Cost Function and Backpropagation

주어진 Training set에서, neural network의 파라미터들을 피팅하는 learning algorihtm을 배워보도록 하겠다. 우리가 다뤘던 learning algorithm들 처럼, 먼저 network의 파라미터를 fitting하기 위한 cost fucntion에 대해서 살펴보겠다.

우리의 network가 아래와 같다고 가정하자.

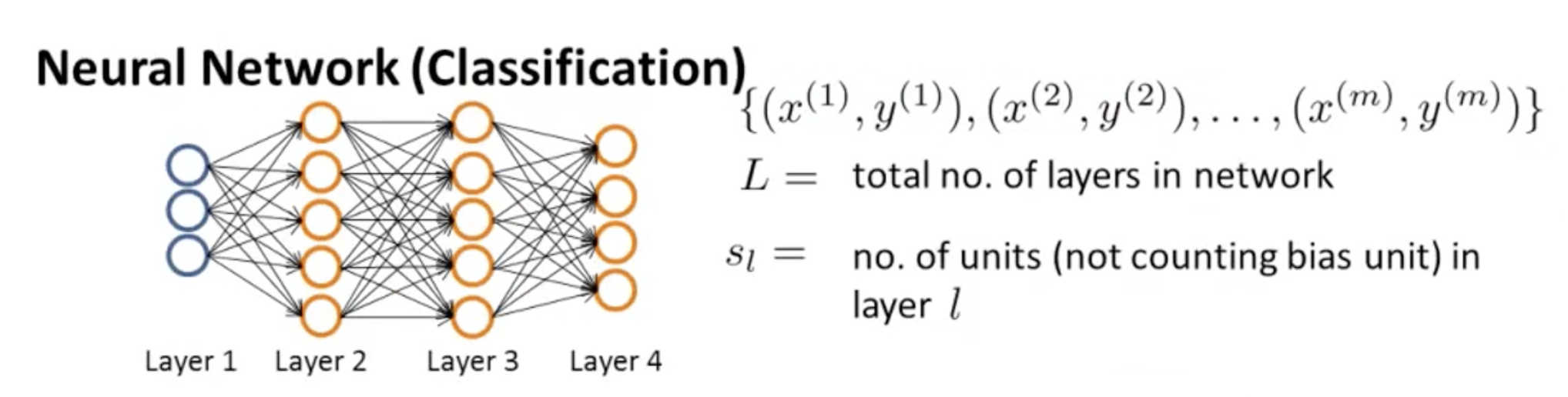
위 그림 오른쪽에 나와있는 기호들을 살펴보자.
우리의 Training set은 x, y의 짝으로 M개의 training examples가 있다.
L은 네트워크의 total number of layers니까 4라고 할 수 있고,
$s_l$ 은 bias unit을 제외한 unit의 갯수이다. 여기서 $s_1=3, s_2=5,s_4=s_L=4$ 이다.

두 개 타입의 classification에서 어떻게 달라지는지 살펴보자.
먼저 binary classification이다. $y=0 \;or \;1$ 이고 이 경우 output unit은 오직 1개이다. 따라서 $h_Θ(x)∈ℝ$ 이고, $s_L=1$ 이다(L은 Layer의 갯수이고, 이것은 Output layer와 같기 때문이다.).
Multi-class classification에서는 $y∈ℝ^K$ 이다. 앞선 예시에서,

y^{(i)}=\begin{bmatrix} 1\\ 0\\0\\0\end{bmatrix},\begin{bmatrix} 0\\ 1\\0\\0\end{bmatrix},\begin{bmatrix} 0\\ 0\\1\\0\end{bmatrix},\begin{bmatrix} 0\\ 0\\0\\1\end{bmatrix}

을 보았다. 이렇게 multi classification에서는 y가 여러 값이 나올 수 있고, K개의 output units이 있다고 할 수 있다. 따라서 $h_Θ(x)$ 도 $h_Θ(x)∈ℝ^K$ 이고, $s_L=K$ 이다. 그리고 이 경우, 항상 우리는 3보다 같거나 큰 K를 갖는다. 이유 생각해보기!

Cost Function

우리가 NN에서 쓰는 Cost function은 logistic regression의 generalization 버전이다. Logistic Regression에서, 우리는 cost function $J(\theta)$ 를 최소화 했어야 했는데, Cost Function $J(\theta)$ 공식은 다음과 같다.

Cost Function of Logistic Regression
$J(\theta) = -\frac{1}{m}[\sum\limits_{i=1}^my^{(i)}log(h_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)})]+\frac{λ}{2m}\sum\limits_{j=1}^n\theta_j^2$

Neural network에서 우리의 cost function은, 이것을 K개의 Output에 대해 generalization한 것이 될 것이다. Logistic Regression에서의 $y{(i)}$ 는 binary classification을 위한 것이기 때문이다. 따라서 NN에서의 cost function은 다음과 같다.

Cost Function of Neural Network
$h_Θ(x)∈ℝ^K$ $(h_Θ(x))_i= i^{th}\;output$ $J(\Theta)=-\frac{1}{m}[\sum\limits_{i=1}^m\sum\limits_{k=1}^Ky_k^{(i)}log(h_{\Theta}(x^{(i)})_k+(1-y^{(i)}_k)log(1-h_{\Theta}(x^{(i)})_k]+\frac{λ}{2m}\sum\limits_{l=1}^{L-1}\sum\limits_{i=1}^{s_l}\sum\limits_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2$

Backpropagation Algorithm

Cost Function을 minimize할 수 있는 알고리즘인 backpropagation algorithm을 살펴보자.

우리는 Cost Function $J(\Theta)$ 를 minimize할 수 있는 $\Theta$ 를 찾고 있다. Gradient Descent나 advanced optimization algorithm을 사용하기 위해선, cost function $J(\Theta)$ 와 편미분 $\frac{∂}{∂\Theta_{ij}^{(l)}}J(\Theta)$ 를 계산해야 한다. 여기서 ${\Theta_{ij}^{(l)}}∈ℝ$ 인 걸 기억해야 한다. 과연 $\frac{∂}{∂\Theta_{ij}^{(l)}}J(\Theta)$ 는 어떻게 계산할 수 있을까?

먼저 우리는 오직 하나의 training example $(x, \;y)$ 가 있다고 가정하자. hypothesis를 계산하기 위해 forward propagation을 적용하자. 이를 나타내면 아래와 같다.

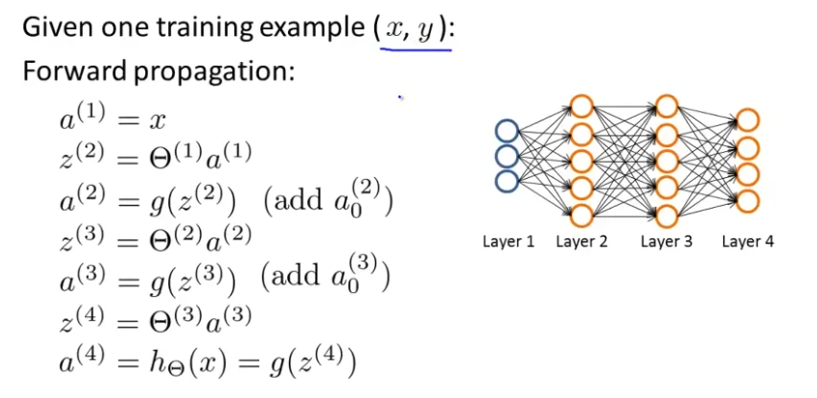
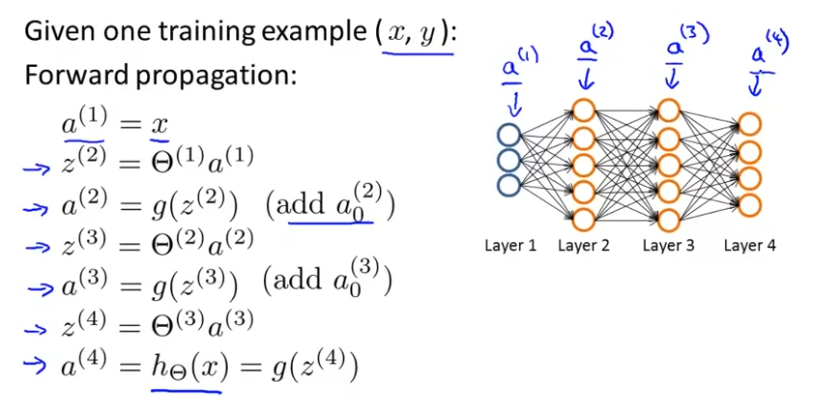
forward propagtion은 Input Layer에서 출발해서 hypothesis를 구할 수 있다.

Backpropagation은 output layer에서 시작한다. Backpropagation algorithm의 intuition은 layer $l$ 에 있는 node $j$ 의 에러를 나타내는 $\delta_j^{(l)}$ 를 계산하는 것이다. $a_j^{(l)}$ 은 layer $l$ 에 있는 $j$ 번째 activation node인 것을 다시 상기시켜보면, $\delta_j^{(l)}$ 은 activation $a_j^{(l)}$ 에 있는 에러를 나타낸 다는 것을 알 수 있다. 이 예시에서 $\delta_j^{(l)}$ 를 계산해보면 아래와 같다.

For each output unit (layer L=4)
$\delta_j^{(4)}=a_j^{(4)}-y_j$ (단, $a_j^{(4)} = (h_Θ(x))_j$ )
$\delta_j^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g'(z^{(3)})$
$\delta_j^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g'(z^{(2)})$
(No $\delta_j^{(1)}$ because Layer1 is input layer)
$g'(z^{(l)})=a^{(l)}.*(1-a^{(l)})$ 로 나타낼 수 있다. 증명 과정은 여기서 다루지 않는다.

이제 한 훈련세트가 아닌 거대한 훈련세트를 가지고 있을 때, 어떻게 backpropagation을 구할 수 있는지를 알아보겠다. Backpropagation algorithm은 다음과 같다.

Training Set이 $\{(x^{(1)},y^{(1)}),\;...\;,(x^{(1)},y^{(1)})\}$ 로 m개가 있다고 가정하자.
모든 $l,i,j$ 에 대하여, $\Delta_{ij}^{(l)}=0$ 을 만족하게 할 것이다. 결국 이 $\Delta_{ij}^{(l)}$ 는 편미분항 $\frac{∂}{∂\Theta_{ij}^{(l)}}J(\Theta)$ 을 계산하게 되고, 편미분항을 계산하기 위해서 값들을 저장하는 accumulator가 된다.
훈련세트 전체에 대한 for loop를 돈다.
1. input layer의 activation인 $a^{(1)}$ 에 우리의 training example $x^{(i)}$ 를 대입한다.
2. $l=2,3,4...,L$ 인 layer $l$ 에 대해서 $a^{(l)}$ 을 구하기 위해 forward propagation을 수행한다. $a^{(L)}$ 은 hypothesis의 출력이 된다.
3. $y^{(i)}$ 를 이용해서, $\delta^{(L)}=a^{(L)}-y^{(i)}$ 를 구한다.
4. back propagation algorithm을 사용해서, $\delta^{(L-1)},\delta^{(L-2)},...,\delta^{(2)}$ 를 계산한다. 입력 레이어는 에러와 관련이 없기 때문에 $\delta^{(1)}$ 은 고려하지 않는다.
5. 편미분항을 축적하기 위해서, $\Delta_{ij}^{(l)}:=\Delta_{ij}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}$ 를 수행한다. $\Delta_{ij}$ 를 벡터라고 생각하고, $i,j$ 로 요소를 표현하여 이를 벡터화 시키면 다음과 같다. $\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T$
$j≠0$ 일 때, $D_{ij}^{(l)}:=\frac{1}{m}(\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)})$ 이고, $j=0$ 일 때, $D_{ij}^{(l)}:=\frac{1}{m}\Delta_{ij}^{(l)}$ 이다. $j=0$ 일 때 bias항에 대응되기 때문에 추가적인 정규화항이 있다.
$\Delta_{ij}^{(l)}$ 를 계산해보면, 이것는 각 매개변수에 대한 cost function의 편미분과 같다.( $\Delta_{ij}^{(l)}=\frac{∂}{∂\Theta_{ij}^{(l)}}J(\Theta)$ ) 이걸 Graident Descent나 다른 고급 알고리즘에서 사용할 수 있다.

Backpropagation in Practice

지금까지 미분을 계산하기 위해서 Neural Network에서 forward propagation과 backpropagation을 어떻게 해야하는지 살펴보았다. 하지만 back propagation은 알고리즘으로서 많은 디테일과 구현하기 어려운 것들을 가지고 있다. 그리고 back propagation의 하나의 단점은 미묘한 버그를 가지는 많은 방법이 있다는 것이다. 따라서 gradient descent나 다른 알고리즘을 작동시킨다면, 이게 잘 작동하는 것처럼 보일 수 있다. cost function $J(\theta)$ 가 gardient descent의 모든 interation에서 줄어들기 때문이다. 하지만 결과적으로 높은 레벨의 error을 가지는 neural network를 마무리 짓게 될 것이다. 그럼 어떻게해야할까? gradient checking을 이용해볼 수 있다. gradient checking을 이용하면, back prop에서 buggy implementation 문제들을 아주 많이 줄일 수 있다.

Gradient Checking

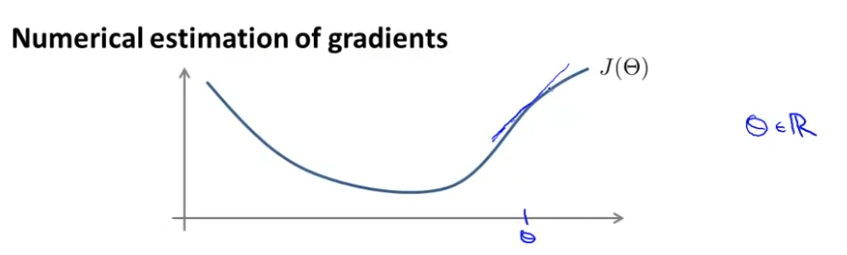
다음과 같은 cost function $J(\theta)$ 가 있다고 가정하자. 그리고 다음과 같은 지점에서 $\theta$ 를 가진다고 가정하자. 이 함수의 $\theta$ 지점에서 도함수를 알기 위해선, slope의 tangent값과 같다.

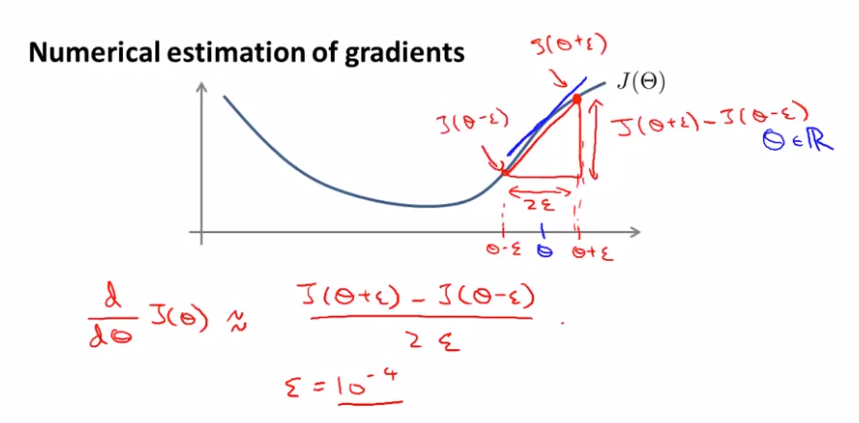
수학적으로 도함수의 근사치를 알아내보자. $\theta$ 에서 아주 작은 숫자 $\epsilon=10^{-4}$ 만큼 좌우로 떨어져있는 지점이 있다고 하자. 이 두 지점을 연결한 것이 빨간색 선이다. 도함수와 도함수의 근사치를 꽤 잘 맞는 것을 확인할 수 있다.

이제 parameter vector $\theta$ 에 대해서 살펴보자.

각 편도함수 $\frac{∂}{∂\theta_{i}}J(\theta)$ 는 위처럼 근사치를 얻을 수 있다.

Random Initialization

gradient descent나 advanced optimization algorithms를 사용할 때, 우리는 initial value $\Theta$ 를 선택해야한다.!

먼저, 모든 $i,j,l$ 에 대하여, 만약 $\Theta_{ij}^{(l)}$ 을 모두 0으로 초기화, 즉, 모든 weight들을 0으로 초기화 하게 되면 어떨까?

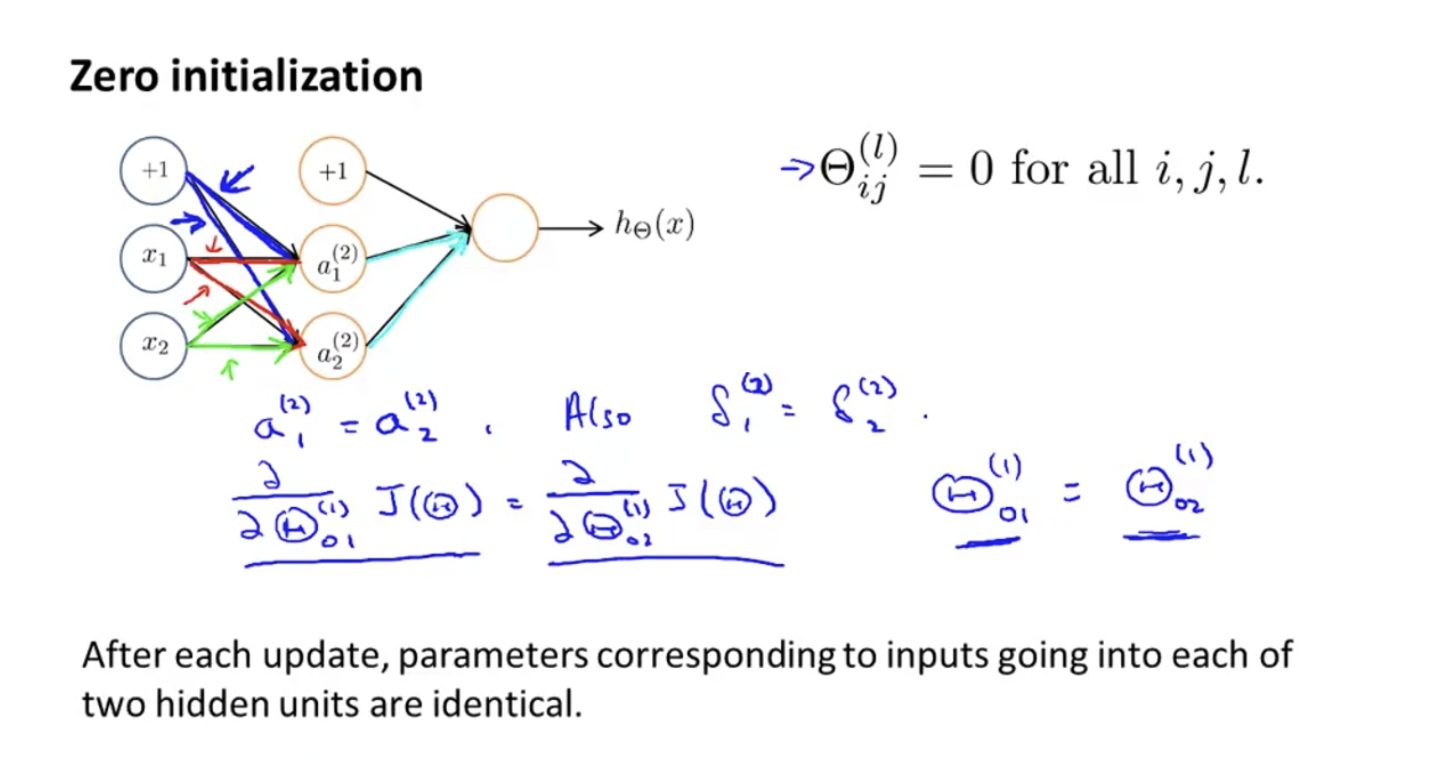
같은 색으로 표시된 간선들은 같은 값을 가지므로 $a_1^{(2)}=a_2^{(2)}$ 가 되고, $\delta_1^{(2)}=\delta_2^{(2)}$ 가 된다. 따라서, 각 업데이트 마다, 같은 input 에서 나온 weight들은 같다. 이것은 올바른 값이 아니다. 따라서 neural network에서 weight들은 0으로 초기화하면 제대로 작동하지 않는다. 따라서 random initialization을 사용한다.

앞선 문제를 the problem of symmetric ways라고 부르는데, 이제 사용할 Random initialization은 symmetric breaking을 어떻게 수행하는지를 보여준다.

각 parameter들은 랜덤으로 $-\epsilon$ 부터 $\epsilon$ 사이의 값 중 하나로 초기화된다.

이 방법을 이용하면 gradient descent나 advanced optimization algorithms를 사용할 때, initial value $\Theta$ 를 잘 선택할 수 있다.

Putting It Together

이제 앞서 배웠던 모든 것들을 이용해서 어떻게 neural network learning algorithm를 구현하는지 알아보자.

0. 먼저, network architecture을 선택한다.

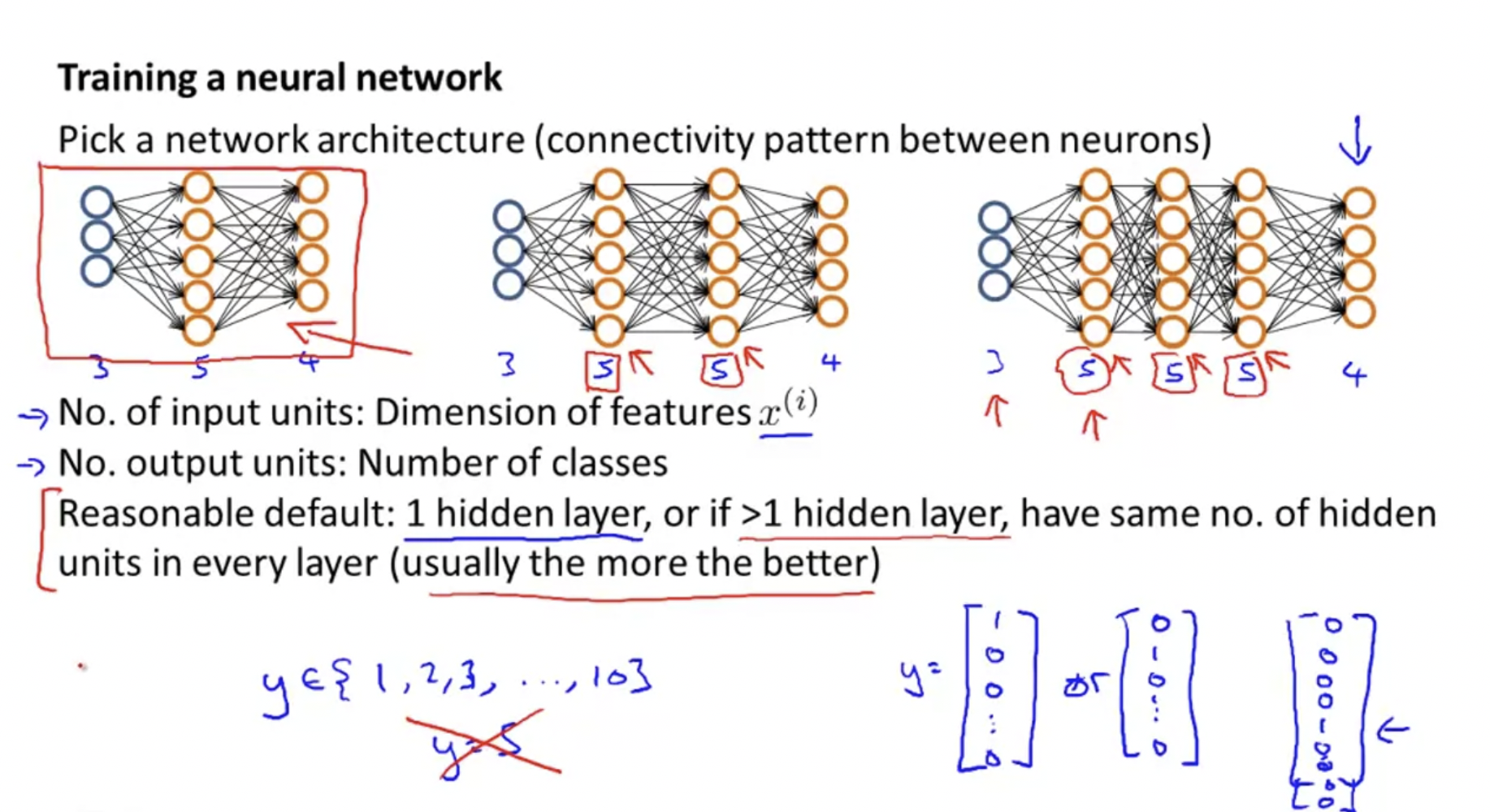
각 layer에 얼마나 많은 hidden units이 있는지 그리고 얼마나 많은 layer를 가질 것인지를 따져서 선택한다.

Number of input units = dimension of features $x^{(i)}$
Number of output units = number of classes
Number of hidden units per layer = usually more the better (must balance with cost of computation as it increases with more hidden units)
Defaults: 1 hidden layer. If you have more than 1 hidden layer, then it is recommended that you have the same number of units in every hidden layer.

기억해야할 점은, 만약 $y∈\{1,2,3,...,10\}$ 일 때, 이것은 벡터로 $y=\begin{bmatrix} 1\\ 0\\ ...\\ 0 \end{bmatrix},\begin{bmatrix} 0\\ 1\\ ...\\ 0 \end{bmatrix},\begin{bmatrix} 0\\ 0\\ ...\\ 1 \end{bmatrix}$ 이렇게 나타낼 수 있다.

1. Random Initialization을 통해 weight를 초기화한다.
2. forward propagation로 $h_\Theta(x^{(i)})$ 를 구한다.
3. cost function $J(\Theta)$ 를 구하는 코드를 구현한다.
4. backpropagation으로 partial derivatives $\frac{∂}{∂\theta_{jk}^{(l)}}J(\theta)$ 을 구한다.
5. gradient checking을 통해 backpropagation이 잘 작동하는지 확인한다. 그 뒤에 꼭 gradient checking code를 disable한다. 왜냐하면, gradient checking code는 연산속도가 느리기 때문이다.
6. gradient descent나 built-in optimization function을 사용해서 cost function을 minimize한다.