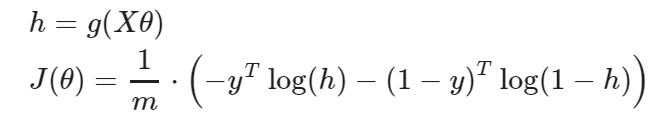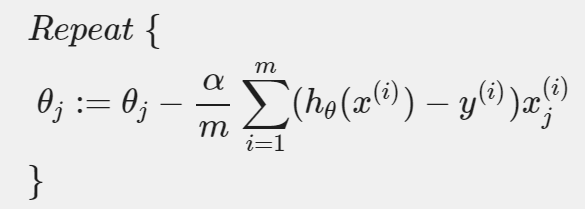[ML] Classification

Classification 예시

Email : Spam / Not Spam
온라인 거래 : 물건을 파는 웹 사이트에서 도용인지 아닌지
종양 : 악성인지 아닌지

지금까지 논의한 문제들은 모두 0또는 1 둘 중의 하나의 값을 가지는 변수 y를 예측하는 것이다.

0으로 분류 되는 것을 negative class(음성분류), 1로 분류되는 것을 positive class(양성분류)라고 한다.
다음 시간엔 다중 분류(Multiclass Classification) $y ∈ {0, 1, 2, 3}$ 등의 여러가지 y값을 찾는 분류 문제도 다룰 예정이다.

Classification을 적용하는 방법

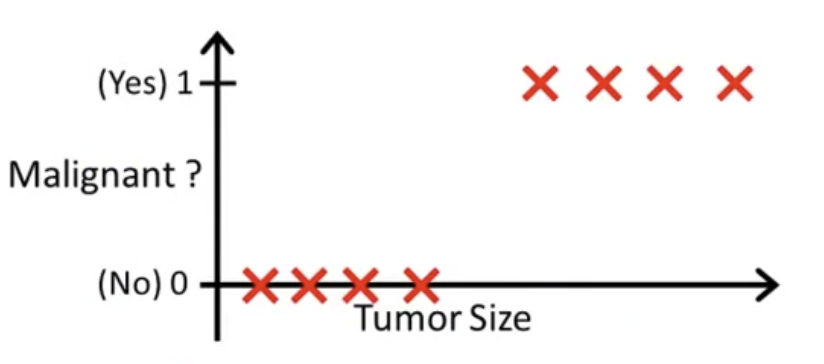
다음과 같은 악성/양성 종양 구분을 위한 training set이 있다. 여기에 우리가 일미 알고 있는 Linear Regression 알고리즘을 적용할 수 있다. 즉, 직선 그래프에 데이터를 맞추는$h_\theta(X)=\theta^TX$를 적용하는 것이다. 여기서 $X$는 행렬이다.

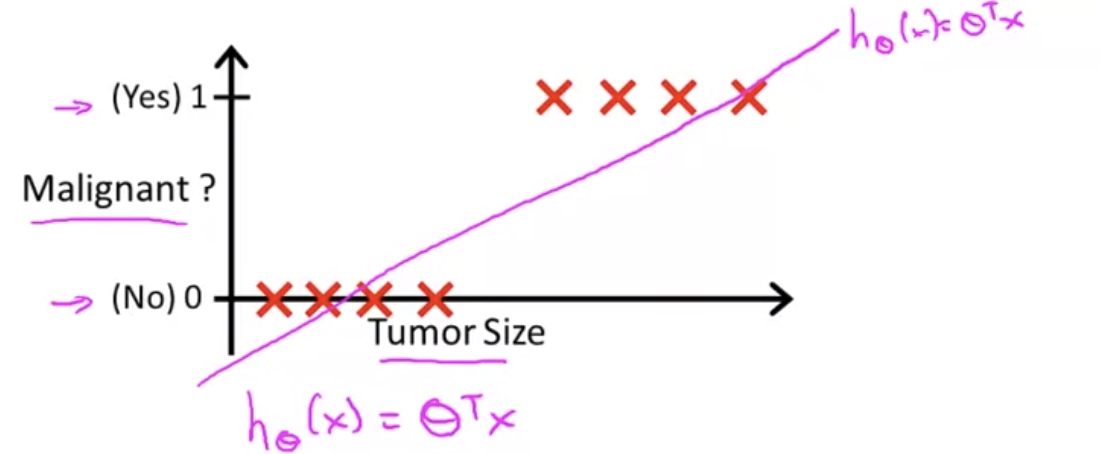
여기서 $h_\theta(x)$의 결괏값이 0.5가 되는 곳에 수직 threshold을 긋는다. 0.5보다 작은 경우, y=0으로 예상하고, 같거나 큰 경우 1이라고 할 수 있다.
이렇게 threshold를 설정하는 것이 Linear Regression을 사용하는 방법이 된다.

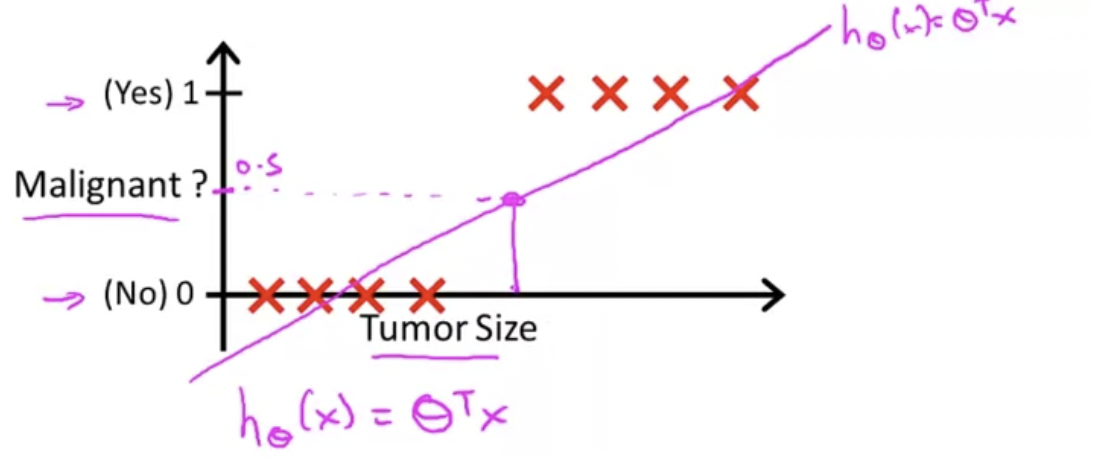
위 그림과 같이 말이다.

이 예시에서 선형회귀가 마치 합리적으로 보일 수 있지만, 문제를 조금 바꾸면 어려울 수 있다.

수평축을 늘리고 오른쪽 끝에 훈련 데이터를 하나 더 추가해보자.

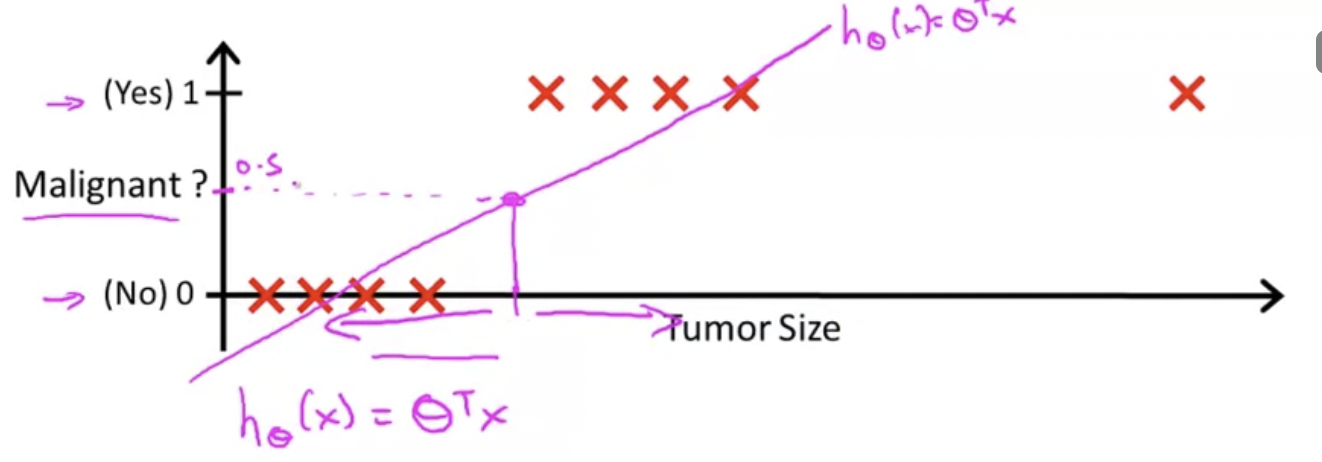
이 추가된 부분을 주목해보면 여기에 하나가 생겼을 뿐 나머지 트레이닝 셋은 그대로 전혀 바뀌지 않았다. 이제 이렇게 생긴 training set을 보면, 어떤게 좋은 hypothesis인지를 알 수 있다.
처음에 있었던 training set에서 y가 0.5인 값을 기준으로 tumor size가 왼쪽이면 음성, 오른쪽이면 양성이라고 예측했다.

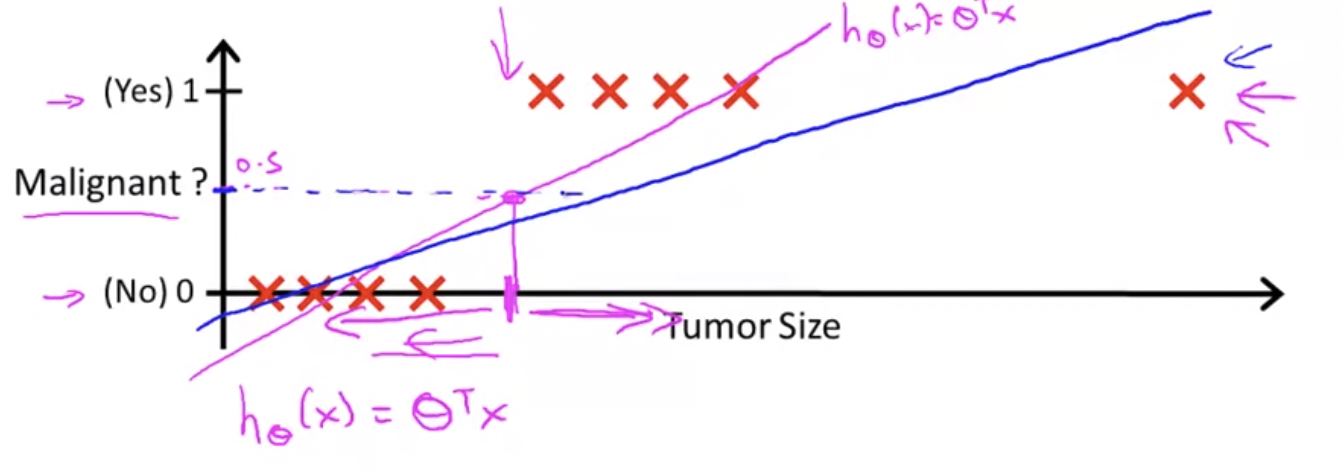
이제 다음과 같은 hypothesis를 그릴 수 있고, y가 0.5인 값을 기준으로 tumor size가 왼쪽이면 음성, 오른쪽이면 양성이라고 예측한다. 하지만 결론적으로 좋지 않은 결과를 얻었다. 양성인 값을 음성, 음성인 값을 양성으로 예측값($h_\theta(x)$)을 얻게 된다.

그러므로 선형회귀를 분류 문제에 적용하는 것은 대부분 좋은 생각이 아니다.

Hypothesis Model of Logistic Regression

이번엔 Logistic Regression대해서 알아보자. Regression이라는 말 때문에 회귀문제 같지만, 이는 분류에 속한다.
Classification 문제에서 결괏값이 0과 1사이가 되도록 한다고 말했다. 즉, 다음과 같다.

그래서 우리는 이러한 결과값을 만족하는 가설, 즉 예측값이 0과 1사이인 가설을 만들고 싶다.
Linear Regression에서 가설 형식은 다음과 같았다.

Sigmoid Function (Logistic Function)을 사용해서, 다음과 같이 바꿀 수 있다.

참고로 Sigmoid Function(Logistic Function)은 이렇게 생겼다


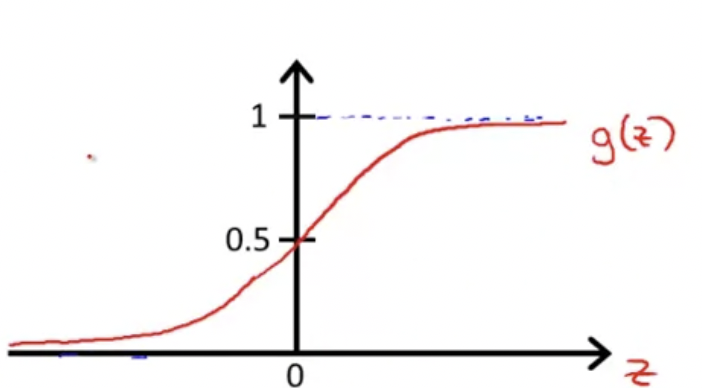
z값의 수평축을 기준으로 z가 음의 무한대로 가면 0에 수렴하고, 양의 무한대로 갈수록 1에 수렴한다.

따라서 $h_\theta(x)$는 다음과 같다.

$h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}$

이제 이 hypothesis $h_\theta(x)$는 input x에 대하여, output이 1일 추정 확률이라고 말할 수 있다.
만약, $h_\theta(x)=0.7$이면, output이 1일70%의 확률을 가졌다고 할 수 있다.
따라서 $h_\theta(x)$를 다음과 같이 쓸 수 있다.

이 뜻은, $\theta$로 parameterized된 x에 대하여, y=1일 확률과 같다.

이제, 이것은 분류 문제이기 때문에 y=0 or 1이라는 것을 알고 있다. 따라서 다음과 같은 성질이 성립한다.

또, 이것은 다음과 같이 나타낼 수 있다.

Decision Boundary

Decision Boundary

Logistic regression이 다음과 같았다.

$h_\theta(x)=g(\theta^Tx) \\g(z) = \frac{1}{1+e^{-z}}$

$h_\theta(x)≥0.5$이면, $y=1$을 예측하고,
$h_\theta(x)<0.5$이면, $y=0$을 예측한다고 하자.

먼저 $h_\theta(x)≥0.5$이면, $y=1$을 예측하는 상황을 살펴보자.
우리는 $z≥0$이면, $g(z)≥0.5$인 것을 알 수 있다. ···(ㄱ)
hypothesis for logistic regression이 $h_\theta(x)=g(\theta^Tx)$이기 때문에,
(ㄱ)에 의해 $\theta^Tx≥0$이면, $h_\theta(x)=g(\theta^Tx)≥0.5$가 될 것이다.

$h_\theta(x)<0.5$이면, $y=0$을 예측하는 상황을 살펴보자.
위와 마찬가지로,
$h_\theta(x)=g(\theta^Tx)$이기 때문에, $\;\theta^Tx<0$이면, $h_\theta(x)=g(\theta^Tx)<0.5$이다.

이제 적용해보자!

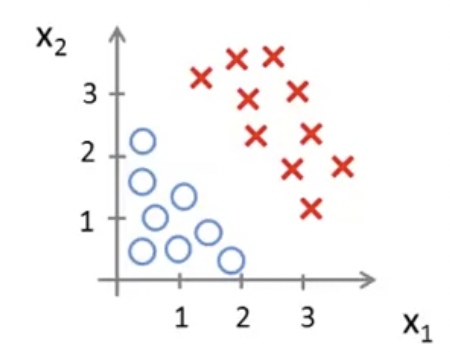
위와 같은 data set이 있다고 가정하자.
$h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$에서,
$\theta_0=-3$, $\theta_1=1$, $\theta_2=1$일 때, 즉, $\theta = \begin{bmatrix}-3\\1\\1\\ \end{bmatrix}$일 때, $h_\theta(x)=g(-3+x_1+x_2)$라고 할 수 있다.
따라서, $z=-3+x_1+x_2$에서 (즉, $\theta^Tx=-3+x_1+x_2$), $z≥0$이면 ($-3+x_1+x_2≥0$ 이면) $y=1$, $z<0$이면($-3+x_1+x_2<0$ 이면) $y=0$이다.
$x_1+x_2=3$을 기준으로 $y$값이 바뀌기 때문에, 이를 그래프에 그려보면

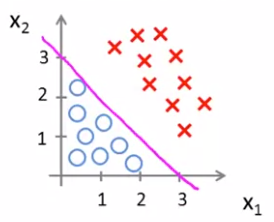
마젠타 색의 직선을 기준으로 영역이 나뉘는 것을 확인할 수 있다.

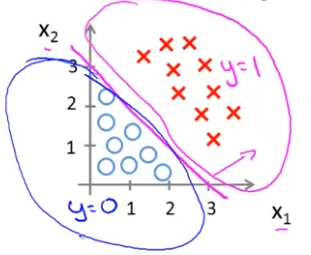
$x_1+x_2=3$을 기준으로, $x_1+x_2<3$이면 $y=0$인 영역이고, $x_1+x_2≥3$이면 $y=1$인 영역이다. 이렇게 기준이 되는 선을 Decision Boundary라고 한다.
$\theta_0,\theta_1,\theta_2$을 알고 있으면 Decision Boundary를 나타낼 수 있다.

Non-linear Decision Boundary

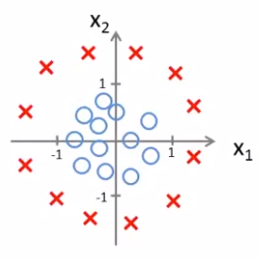
이번엔 좀 더 복잡한 예제를 살펴보자. X는 positive examples이고, O는 negative examples이다. 이런 구조가 있을 때 어떻게 이 data의 부분에 딱 맞는 logistic regression을 찾을 수 있을까?
앞에서 우리가 polynomial regression 또는 linear regression에 대해 말했을 때, 우리는 어떻게 더 높은 차원의 polynomial terms를 추가하는지 배웠다. logistic regression에서도 똑같이 적용한다.

hypothesis가 다음과 같다고 하자.

다음 비디오에선 어떻게 자동적으로 $\theta$들을 선택하는지 배울거지만, 일단 지금은 $\theta$가 다음과 같다고 가정하자.

따라서 $h_\theta(x)=g(-1+x_1^2+x_2^2)$이고, $z=-1+x_1^2+x_2^2$ 이다.
$-1+x_1^2+x_2^2≥0$이면 $y=1$이고, $-1+x_1^2+x_2^2<0$이면 $y=0$이다. 즉, $+x_1^2+x_2^2=1$을 기준으로, $x_1^2+x_2^2≥1$이면 $y=1$이고, $x_1^2+x_2^2<1$이면 $y=0$이다.

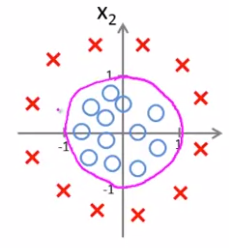
따라서 decision boundary는 다음과 같고, 이 boundary 밖에 있으면 $y=1$이고, 안에 있으면 $y=0$이다.

이것보다 더 높은 차수라면 더 복잡한 decision boundary를 만들어낼 수 있다.

sigmoid function $g(z)$에 대한 입력은 선형일 필요가 없다.
다음엔 어떻게 자동으로 parameter을 알 수 있는지 알아보자.

Cost Function

다음과 같은 logistic regression model에 맞춘 Supervised learning problem이 있다.

Training Set : ${(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}$
m examples : $x∈\begin{bmatrix}x_0\\x_1\\...\\x_n\\ \end{bmatrix}$ $x_0=1, y∈{0,1}$
$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$

여기서 어떻게 $\theta$를 찾아낼 수 있을까?

Cost Function에 대해서 살펴보자.
Linear Regression에서 Cost Function은 $J({\theta}) = \frac{1}{m}{\sum\limits_{i=1}^m}\frac{1}{2}(h_{\theta}(x^{(i)}) - y^{(i)})^2$ 이었다.
$Cost(h_\theta(x^{(i)}),y^{(i)})=\frac{1}{2}(h_{\theta}(x^{(i)}) - y^{(i)})^2$ 이라고 하자.
Logistic Regression에서 Cost Function은 다음과 같다.

단, $Cost(h_\theta(x^{(i)}),y^{(i)})=\frac{1}{2}(h_{\theta}(x^{(i)}) - y^{(i)})^2$

여기서의 Cost Function은 non-convex function (비블록함수)이다.

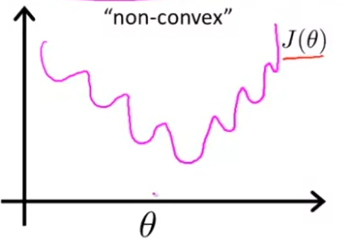
아주 많은 극솟값을 가지고 있는데 이런 비블록함수는 Gradient Descent를 적용해도, local minimum에 도달할 수 있다는 보장이 없다. 반면에 convex function (블록함수)인 경우 cost function $J(\theta)$는 다음과 같다.

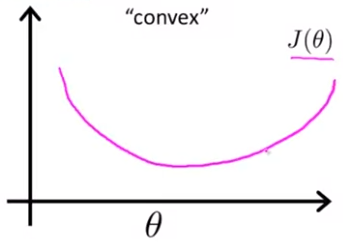
이는 활 모양으로 한번만 구부러진 모양이고 Gradient Descent를 적용하면 전체 함수의 local minimum에 도달할 수 있다.
그래서 우리는 다른 Cost Function을 제공해야 한다.
진짜 Logistic Regression에서 Cost Function은 다음과 같다.

$J(\theta) = \frac{1}{m}{\sum\limits_{i=1}^m}Cost(h_\theta(x^{(i)}),y^{(i)})$

단, $Cost(h_\theta(x^{(i)}),y^{(i)})= \begin{cases} -log(h_\theta(x)),\;if\;y=1\\ -log(1-h_\theta(x)),\;if\;y=0 \end{cases}$

이를 그래프로 그려보면 다음과 같다.


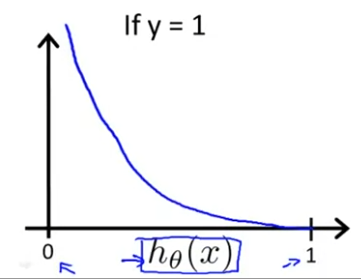
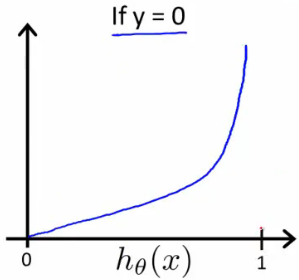
이 비용함수는 다음과 같은 속성을 가진다.

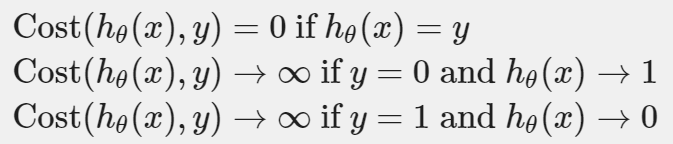
Simplified Cost Function and Gradient Descent

Simplified Cost Function

$J(\theta) = \frac{1}{m}{\sum\limits_{i=1}^m}Cost(h_\theta(x^{(i)}),y^{(i)})$

단, $Cost(h_\theta(x^{(i)}),y^{(i)})= \begin{cases} -log(h_\theta(x)),\;if\;y=1\\ -log(1-h_\theta(x)),\;if\;y=0 \end{cases}$
$Note \;that\; y=0\;or\;1 \;always.$

라고 했다. y=0 또는 1이기 때문에, 우리는 좀 더 Cost Function을 간소화할 수 있다. 지금은 조각함수와 같은 형태로 보이지만, 이것을 계단함수를 이용해서 한 줄로 나타낼 수 있고, 이렇게 한 줄로 나타내면 Graident Descent를 사용할 수 있다.

$J(\theta) = \frac{1}{m}{\sum\limits_{i=1}^m}Cost(h_\theta(x^{(i)}),y^{(i)})$

$Cost(h_\theta(x^{(i)}),y^{(i)})=-y^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))$

$Note \;that\; y=0\;or\;1 \;always.$
이를 벡터화하면 다음과 같다.

Gradient Descent

이제 Cost Function을 최소화 하기 위해 Gradient Descent를 사용할 것이다.
우리는 Cost Function $J(\theta)$를 최소화하는 $\theta$를 찾고 싶다.
우리가 자주 사용하는 Graidnet Descent의 식은 다음과 같다.

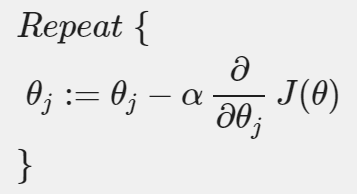
여기서 모든 $\theta$는 동시에 update되어야 한다.

위 Graidnet Descent 식의 $J(\theta)$에 Logistic Regression에서의 Cost Function을 대입하면 다음과 같은 식을 얻을 수 있다.

단, 모든 $\theta_j$는 동시에 update되어야 한다.
즉, 만약 n개의 feature을 쓴다면, $\theta = \begin{bmatrix}\theta_0\\\theta_1\\...\\\theta_n\\ \end{bmatrix}$에 대해 모든 $\theta_j$는 동시에 업데이트 되어야 한다.

이 알고리즘은 linear regression과 똑같아 보인다!
이것을 벡터화 하면 다음과 같다.

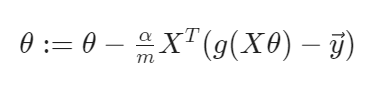
이제 Logistic Regression을 통한 Gradient Descent Alogirhtm을 implement하는 방법을 알았다. 이것은 이 세계에서 굉장히 강력하고 많이 사용되는 알고리즘이다!

Advanced Optimization

이번에는 advanced optimization algorithm을 소개할 것이다. 이런 아이디어들을 사용하면, logistic regression을 더 빠르게 작동시킬 수 있다. 그리고 아주 많은 feature을 가졌을 때 사용해도 굉장히 좋다.

Conjugate Gradient, BFGS, L-BFGS는 $\theta$를 최적화하기 위한 더 정교하고, 빠른 Advanced Opimization Algorithm이다. Gradient Descent 대신에 사용할 수 있다.

장점은 다음과 같다.

• learning rate α를 찾을 필요 없다.
• Gradient Descent보다 빠른 경우가 많다.

단점은 다음과 같다.

• 더 복잡하다.

꼭 이 알고리즘을 스스로 코딩할 필요 없다. Otave에서 이미 test되고 매우 최적화된 라이브러리를 제공하기 때문이다.

예시를 통해 이 알고리즘들을 어떻게 쓰는지 알아보자.

$\theta = \begin{bmatrix}\theta_1\\\theta_2\\ \end{bmatrix}$
$J(\theta)=(\theta_1-5)^2+(\theta_2-5)^2$
$\frac{∂}{∂\theta_1}J(\theta)=2(\theta_1-5)$
$\frac{∂}{∂\theta_2}J(\theta)=2(\theta_2-5)$

위와 같은 상황이 있다고 가정하자. $J(\theta)$가 최소가 되기 위해선 $\theta_1=5,\theta_2=5$여야 한다.
(이하 Otave를 통한 코드 설명 이므로 생략)

One-vs-All을 사용한 Multi-class Classification

이번에는 multi-class classification에서 어떻게 logistic regression을 얻는지에 대해 살펴볼 것이다.

전에 이메일을 분류하는 알고리즘은 스팸인지/아닌지만 분류했다면, 이번에는 일/친구/가족/취미 이렇게 네개의 카테고리로 자동으로 분류하는 알고리즘을 만들어내고 싶다. 각각은 4개의 class로 나뉘어졌다고 할 수 있다.
날씨를 분류하는 알고리즘도, 화창함, 흐림, 비, 눈 이렇게 네 가지로 분류할 수 있다. 이런 것들을 Multi-class Classification Algorithm이라고 한다.

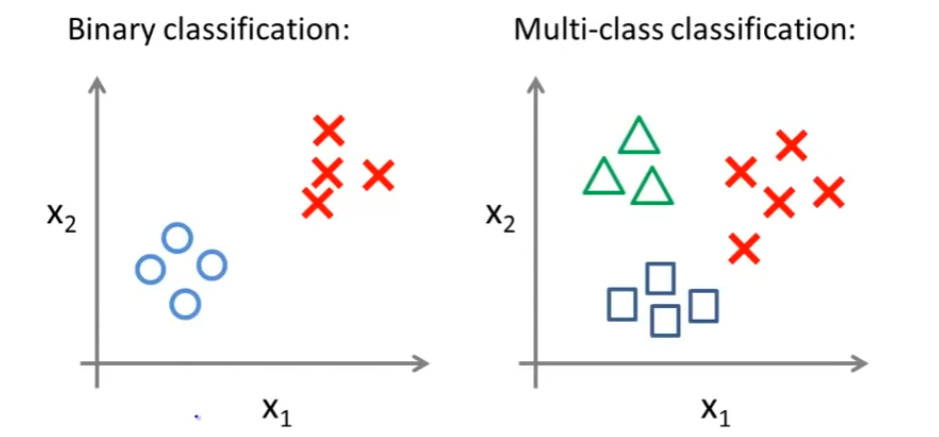
좌측 Binary Classification에선 class를 저렇게 분류했다면, 이번에 Multi-class Classification에선 우측같이 나타낼 수 있다. 3개의 class이기 때문에 세가지의 symbols로 나타냈다.
질문은, 세개 클래스를 가진 데이터 셋이 주어졌을 때, 이 데이터 셋의 분류에 작동하는 learning algorithm을 어떻게 얻어낼 것인가이다.

먼저, one-vs-all classification이라는 아이디어를 살펴보자.

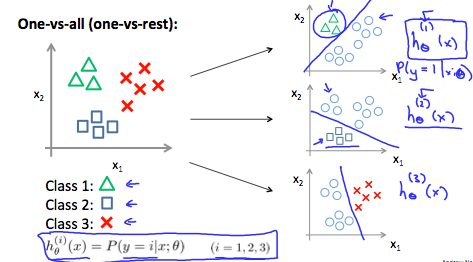
training set을 세개로 분리된 binary classification problems으로 바꾸는 것이다.
Class 1에 대한 binary classification에서 영역을 나눈 직선을 $h_\theta^{(1)}(x)$라ㅏ고 하자. $h_\theta^{(1)}(x)$을 기준으로, 삼각형이 있는 영역을 positive examples, 아닌 영역을 negative examples라고 할 수 있다. Class 2, Class 3에 대한 것도 마찬가지다.
따라서, $h_\theta^{(i)}(x)$ 는 다음과 같이 나타낼 수 있다.

이제 우리는 3개의 classifier을 가지고 있고, 각각은 세 개 클래스 중 하나를 구분할 수 있도록 트레인된 것이다. 즉,

각 class $i$에 대해, logistic regression classifier인 $h_\theta^{(i)}(x)$는 $y=i$에서의 가능성을 예측한다.

새로운 input $x$가 주어진다면, 예측을 위해, 우리가 해야할 것은, 세 개의 $h$를 새로운 $x$에 대해 돌려보고, 최댓값이 나온 class $i$를 고르면 된다. 이를 수식으로 표현하면 다음과 같다.

The Problem of Overfitting

지금까지 우리는 logistic regression, linear regression 같은 많은 알고리즘을 배웠다. 이 알고리즘들은 많은 머신러닝 문제에 쓰일 수 있지만 overfitting이라는 문제에 빠져 성능이 잘 나오지 않을 수 있다. 어떤 영상에서는 overfitting이 무엇인지 설명하고 이후로 몇 개의 영상에서는 regularization이라는 기술에 대해 얘기할텐데 이것들은 학습 알고리즘이 더욱 좋은 성능을 낼 수 있게 한다. 그럼 overfitting이란 무엇일까?

What is the Overffitting

앞서 계속 사용하던 집값 예측 문제를 Linear Regression으로 예측하는 것을 살펴보자.

방법으로는 다음과 같았다.

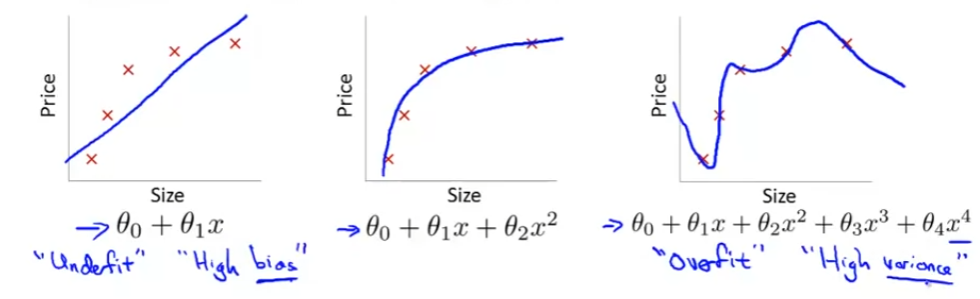
• $y = θ_0 + θ_1x$에선 다음과 같은 문제가 있다.

데이터를 보면 집값이 커지면서 가격이 올라가는 게 보이지만, 집의 사이즈가 커질 수록 집 값이 천천히 올라 평탄화 된다. 그래서 우리의 알고리즘은 잘맞지 않게 됐다. 이런 문제를 underfitting이라고 하고, 높은 편향(높은 바이어스, high bias), 강한 선입견(strong preconception)을 가지고 있다고 한다. 이 두가지 용어는 우리 모델이 데이터에 제대로 맞지 않는다는 것을 뜻한다.

• $y = θ_0 + θ_1x+\theta_2x^2$는 꽤 잘 맞는 모습을 보여준다. Just Right이라고 볼 수 있다.

• $y = θ_0 + θ_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4$에선 다음과 같은 문제가 있다.

다섯개의 파라미터를 통해 데이터에 꼭 맞는 모델을 찾을 수 있는데, 이 선은 데이터에 잘 맞으니 적어도 training set에는 좋은 성능을 내지만, 굉장히 꼬여 있는 선이라 올바르게 집값을 예측할 수 있다고 볼 수 없다. 이런 것을 overfitting이라고 하고, 이것을 다른 말로 high variance(높은 분산)을 가지고 있다고 한다.

따라서, 데이터 셋에 딱 맞는 고차함수를 만들려면 만들 순 있지만, 그렇게 되면 큰 변동성을 갖게 된다. 이런 것을 보고 overfitting이라고 한다.

즉, overfitting은 우리가 너무 많은 feature을 가지고 있을 때, learned hypothesis가 training set에 정말 잘 맞지만, 새로운 example(예측하는 것들)에 대해선 일반화하는 것을 실패하는 것이다.

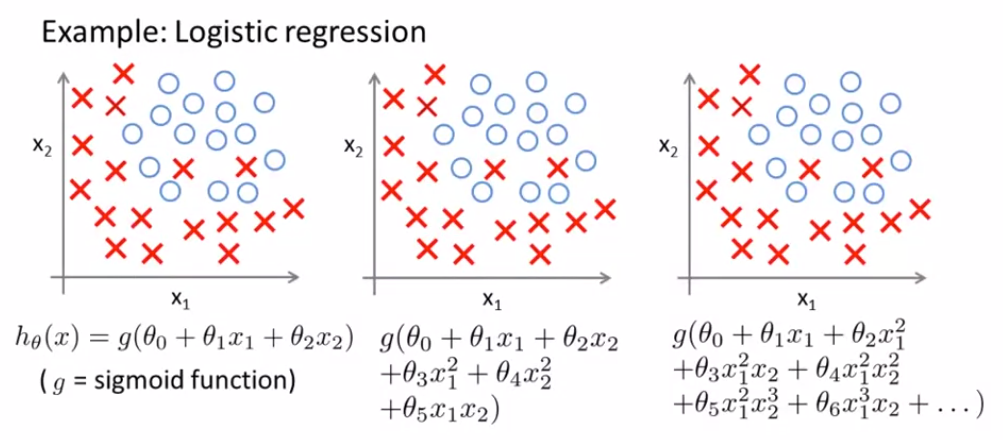
이번엔 Logistic Regression으로 살펴보자. 마찬가지다.

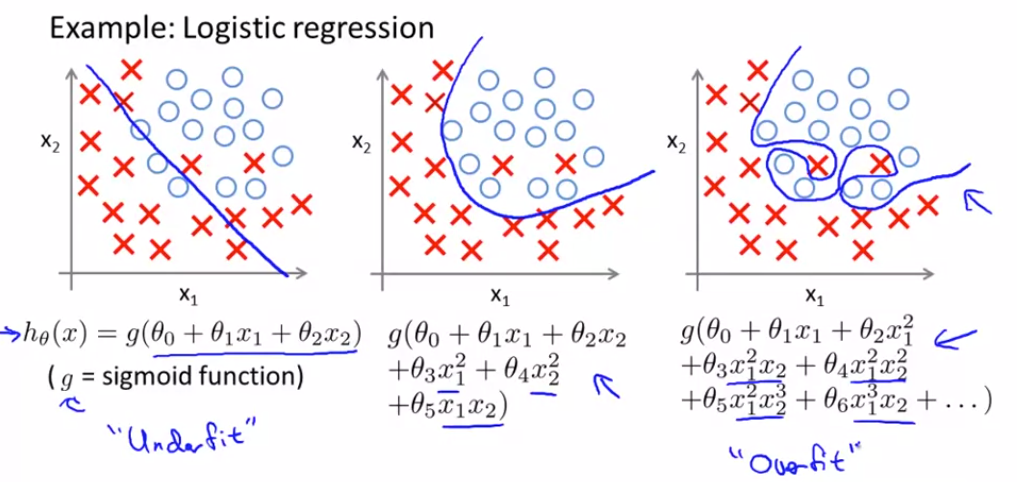
Overfitting인지 알아보고 해결하는 법

어떻게 Overfitting인지 알 수 있을까?
먼저, hypothesis를 그래프로 표현하며 어떤 다항식을 사용하는지 확인한다.

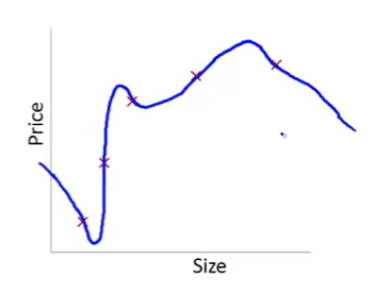
차수가 큰 다항식을 사용하면 Overfitting이 될 확률이 높다. 하지만 항상 동작하는 것은 아니다.

feature이 매우 매우 많아질 수록 그래프를 통해 시각적으로 표현하기 어렵다.

게다가 특성 하나하나가 다 도움이 되어서 줄이기도 쉽지 않다. 이렇게 feature가 매우 많은데 학습 데이터가 적을 때 Overfitting이 발생한다.

해결법은 크게 두 가지가 있다.

1. feature의 갯수를 줄인다.

• 특성을 보고 쓸만하지 않은 특성은 제거한다.
• Model selection algorithm을 사용한다.(나중에 배운다.)

2. Regularization

• 모든 feature을 남기되, $\theta_j$이 미치는 영향을 줄인다.

Cost Function

우리의 hypothesis function으로부터 overffiting이 있을 때, 다음과 같이 할 수 있다.
$\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4$를 더 2차함수로 만들고 싶다.
우리는 \theta_3x^3과 \theta_4x^4의 영향을 줄이고 싶다. 이 feature들을 지우거나 hypothesis의 형태를 바꾸는 것 대신에, 우리는 cost function을 수정함으로서 영향을 줄일 수 있다.

우리는 $\theta_3$와 $\theta_4$를 끝에 덧붙였다. cost function이 0에 가깝게 하기 위해, 우리는 $\theta_3$와 $\theta_44$의 값을 0에 가깝게 줄여야 한다. 이것은 우리 hypothesis 함수의 $\theta_3x^3,\theta_4x^4$를 줄일 것이다.결과적으로, 우리는 2차함수 같으면서도, $\theta_3x^3,\theta_4x^4$가 있어서 data에 더 잘 맞는 같은 새로운 hypothesis 를 얻어낼 수 있다

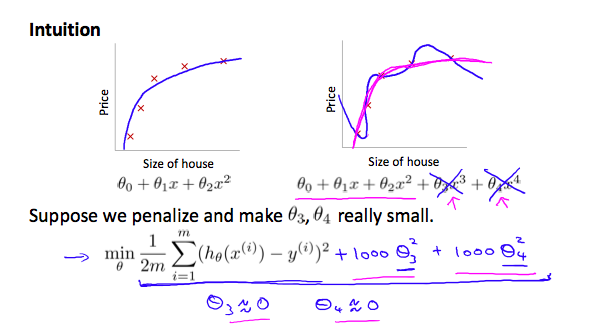
이를 일반화 하면 다음과 같다.

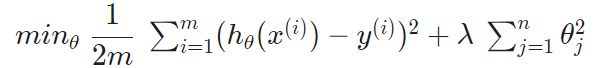
람다 $λ$는 regularization parameter다. 이것은 우리의 $\theta$ parameter의 cost가 얼마나 부풀려졌는지를 결정한다.
이를 사용하면 우리의 hypothesis 함수의 결과에 over fitting이 줄어든다. λ가 크게 선택되면($10^{10}$정도로...), 아주 스무스해져서 underfitting을 초래할 수 있다.

Regularized Linear Regression

우리는 linear regression and logistic regression 모두에 regularization을 적용할 수 있다. 먼저 Linear Regression을 살펴본다.

Gradient Descent

gradient descent function에서 $\theta_0$를 나머지 parameter으로부터 분리해 냄으로써 새롭게 Gradient Descent를 정의할 수 있다. $\theta_0$를 분리하는 이유는 $\theta_0$를 penalize하고 싶지 않기 때문이다. (In machine learning “penalization” is used to avoid/ lessen the overfitting of the model.The concept of penalization is implemented in different ways in different algorithms. Say, The Regression models use regularization where we implement loss function in order to keep the model more generalized.)

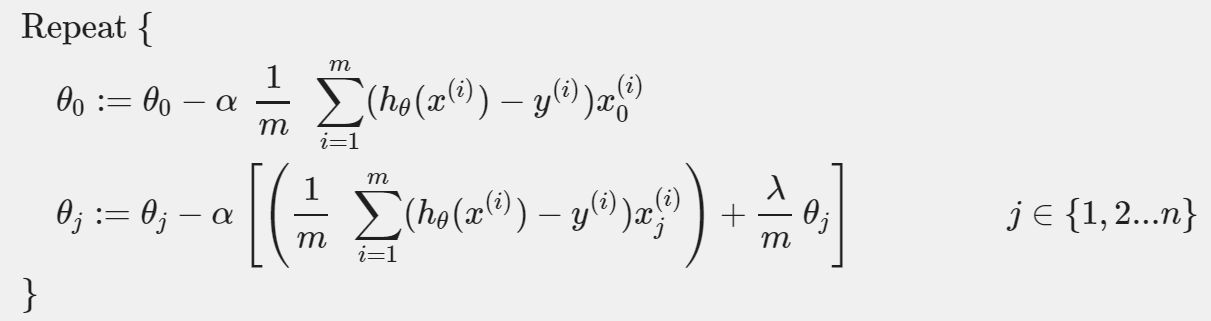
$\frac{λ}{m}\theta_j$가 regularization을 수행한다. 이는 다음과 같이 나타낼 수도 있다.

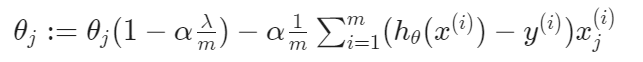
Normal Equation

이번엔 non-iterative normal equation에 regualrization을 적용해보자. regualarization에 더하기 위해서, 괄호 안에 추가적으로 쓴 용어를 제외하고, 방정식은 오리지널과 같아야 된다.

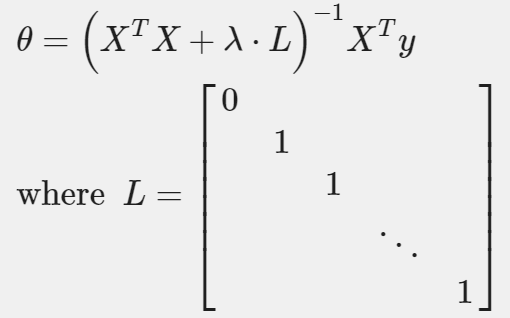
L은 (0,0)이 1이고, 나머지 대각성분은 1인 단위행렬이다. (n+1)x(n+1)차원이다.

Regularized Logistic Regression

Linear Regression과 비슷한 방법으로 logistic regression을 정규화 할 수 있다. 결과적으로, 우리는 overfitting을 피할 수 있다. 아래 이미지에 정규화된 함수 pink line은 정규화 되지 않은 함수 blue line에 비해 어떻게 overfitting을 덜 일으키는지를 보여주고 있다.

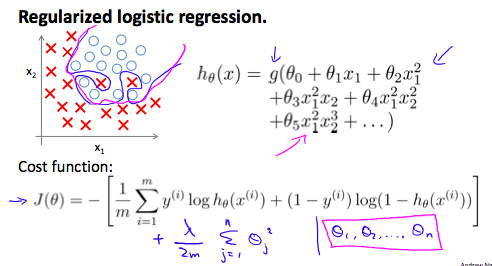
Cost Function

lositic regression에서 cost function은 다음과 같았다.

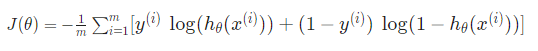
우리는 이 방정식의 끝에 term을 추가해 정규화할 수 있다.

$\sum\limits_{j=1}^n\theta_j^2$이 뜻하는 것은 $\theta_0$를 명백하게 제외하는 것이다. 왜냐하면 $\theta_0$는 bias term이고, bias term은 regularization을 하고싶지 않기 때문이다. 그러므로, 방정식을 계산할 때, 우리는 연달아 두 개의 방정식을 업데이트 해야 한다.