[Machine Learning] Normal Equation

이번엔 특정 Linear Regression문제에서 최적의 파라메터 $\theta$를 구하는데 효과적인 방법이다.

지금까지 선형회귀에 사용됐던 알고리즘은 Gradient Descent였고, 수차례에 걸쳐 알고리즘을 사용해서 여러번 반복하고 나면, global minimum에 수렴하는 방법이였다. 아래 그림과 같이 말이다.

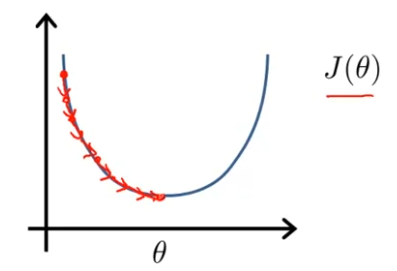
이와는 반대로, normal equation은 $\theta$를 분석적으로 구하는 방법이다. 따라서 여러번 알고리즘을 돌릴 필요 없이 최적의 $\theta$를 한번에 구할 수 있다.
normal equation도 장점과 단점이 있지만, 장단점과 사용시기를 말하기 전에, 어떤 함수인지 개념을 알아보자.

Normal Equation

$\theta ∈ ℝ^{n+1}$에서, $J(\theta_0, \theta_1, ..., \theta_m) = J(\theta)= \frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2$이다.
$\frac{∂}{∂\theta_j} J(\theta)= ... = 0$ (for every $j$)인 $\theta$값을 구하면
cost function이 최소화 되는 $\theta$를 구하는 것이다.

다음과 같은 data set을 가지고 있다고 생각하자.

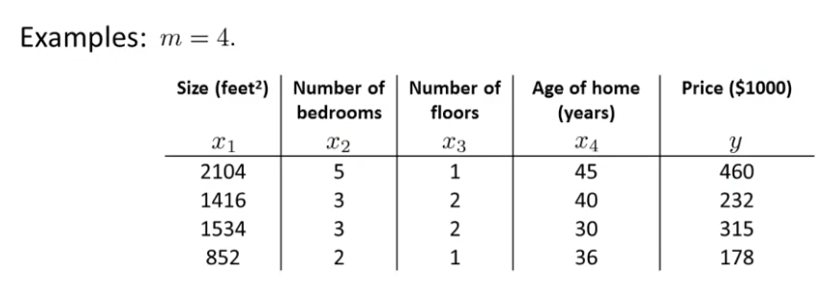
이를 통해 feature들을 가지고 있는 $X$라는 행렬을 만들자. 그러면 다음과 같다.

이는 $(m × n+1)$ 차원 행렬이다.
그리고 y 값을 가지고 있는 $y$행렬을 만들자. 그러면 다음과 같다.

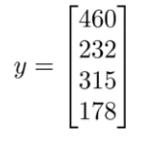
이것은 $m-dimensional\;vector$이다.
행렬 X와 행렬 y를 이용해서 다음 식을 계산하면,

$\theta = (X^TX)^{-1}X^Ty$

이 때의 $\theta$ 값이 cost function을 최소화 하는 값이다.
이를 이용하면 feature scaling은 사용하지 않아도 된다. feature의 범위를 신경 쓰지 않아도 괜찮다.

Gradient Descent vs Normal Equation

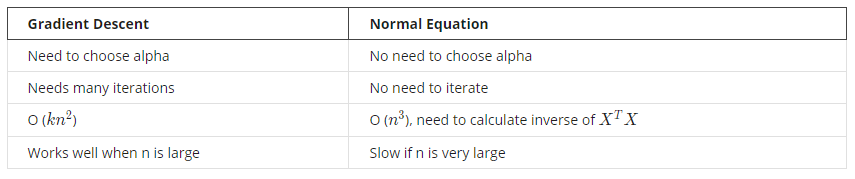
마지막 행에서 n(feature의 갯수)은 10000 이상일 때이다. n이 10000이상이면 gradient descent를 쓰는 것이 훨씬 효율적이다.

역행렬이 없는 경우(Noninvertibility)의 Normal Equation

$\theta = (X^TX)^{-1}X^Ty$에서 만약 $X^TX$가 역행렬을 구할 수 없는 비가역행렬이나 특이행렬이면 어떡할까?
사실, $X^TX$가 역행렬이 없는 경우는 거의 없다. Octave에서도 Normal Equation을 문제 없이 잘 제공해주는데, 사실 Octave에서 역행렬을 구하는 건 두 가지 함수를 제공해준다, pinv()와 inv()이다. 그리고 이 둘은 기술적으로 차이가 있다. 전자는 pseudo-inverse이고, 후자는 그냥 inverse이다. 이에 대한 상세한 차이는 굉장히 어렵기 때문에, 지금 다루지 않지만, 다른 수업에서 $X^TX$의 역행렬이 없는 게 의미하는 게 무엇인지 직관적으로 배울 예정이다.

수학적으로 증명하진 않겠지만, $X^TX$가 역행렬이 없는 경우는 대체로 두가지이다.

• 문제에서 불필요한 feature을 가지고 있는 경우.
• 너무 많은 feature들을 가지고 있는 경우(예:$m≤n$).

따라서 $X^TX$가 역행렬이 없는 경우는, 불필요한 feature을 지우거나, feature가 너무 많은 경우 갯수를 줄이면, 역행렬이 없는 문제를 해결할 수 있을 것이다.