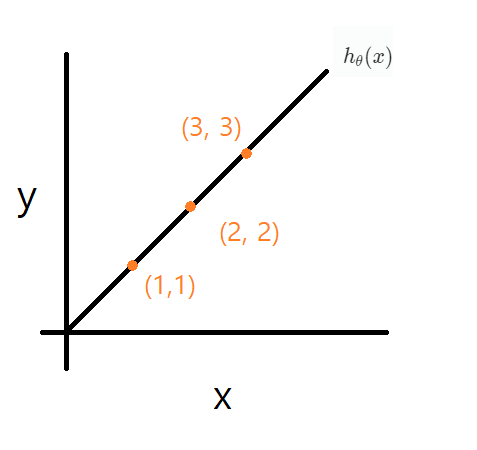[Machine Learning] Linear Regression Model - Cost Function

Cost Function을 사용하면 주어진 데이터에 가장 가까운 일차함수 그래프를 나타낼 수 있다.

Cost Function의 수학적 정의

다음은 앞서 Model Representation (+ Linear Regression)에서 사용했던 모델이다.

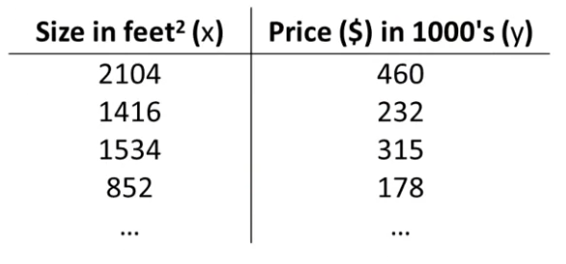
Training Set은 다음과 같다.

Hypothesis는 다음과 같다.

${\theta}_{i's}$ 는 모형들의 모델의 파라메터를 나타내고 있고, 우리가 이 비디오에서 얘기하고자 하는 것은 어떻게 이 두개의 파라미터, ${\theta}_{0}$ 와 ${\theta}_{1}$을 고를 것인지이다.

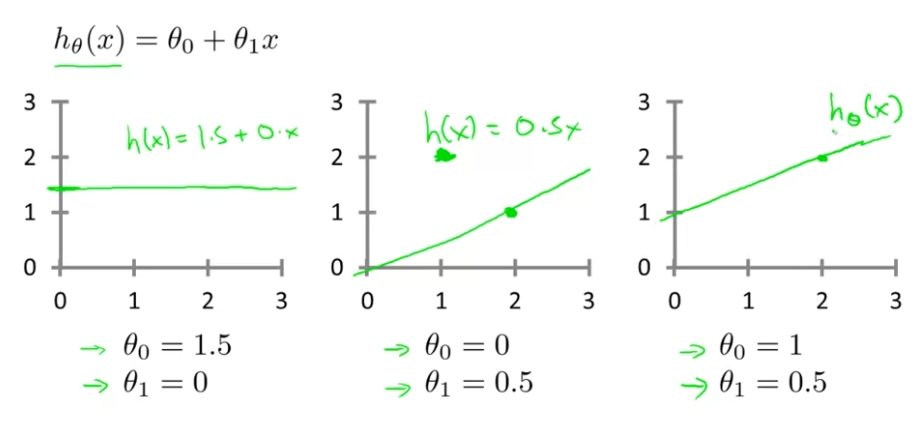
파라메터 ${\theta}_{0}$ 와 ${\theta}_{1}$에서 다른 선택을 하면, 다른 가설, 다른 가설함수들을 가지게 된다. 아래 그림과 같이 말이다.

Linear Regression에서 다음과 같은 Training Set을 가지고 있다고 가정하자.

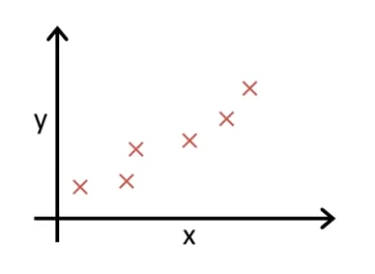
우리가 하려는 것은 ${\theta}_{0}$ 와 ${\theta}_{1}$의 값들을 이용해서 직선을 구할 것이다.

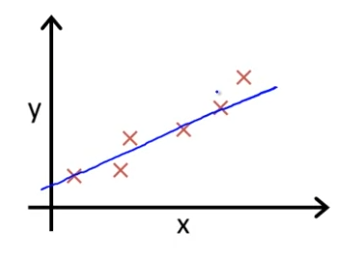
위 그림처럼 말이다. 여기 그린 이 직선처럼 직선이 자료와 얼마나 잘 일치하는지 볼 것이다.
그래서, 우리가 어떻게 해야 ${\theta}_{0}$ 와 ${\theta}_{1}$ 이 데이터들과 잘 일치하는지 알 수 있을까?
${\theta}_{0}$ 와 ${\theta}_{1}$를 골라서 $h_{\theta}(x)$가 training examples $(x, y)$의 $y$랑 아주 가까우면 되지 않을까?
그럼 이를 공식화 해보자. 그럼 Linear Regression에서 최소화 문제를 풀어보자. 최솟값을 ${\theta}_{0}$ 와 ${\theta}_{1}$라고 하자. 그리고 우리는 $(h_{\theta}(x) - y)^2$를 최소화 하려고 한다. 실제 Training Set에선 $(x^{(i)}, y^{(i)})$가 i번째 훈련 예시를 나타내는 것이고, 모든 Training 예시의 최소를 구해야 하므로 i=1부터 m까지의 차이의 제곱의 합계를 구한다. 또, 계산을 좀 더 쉽게 하기 위해 앞에 $\frac{1}{2m}$를 곱하게 할 것이다. 어차피 최솟값을 구하기 위한 것이기 때문에, $\frac{1}{2m}$를 곱하는 걸 두려워하지 않아도 된다. 이는 다음과 같이 나타낼 수 있다.

m은 Training Set의 크기이다.

정리

최소화되는 ${\theta}_{0}$ 와 ${\theta}_{1}$를 찾기 위해서, $\frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2$ 를 구하는 것으로 접근했다. 비용함수를 나타내기 위한 공식은 이 공식이 될 것이다. 원래 목적을 잊지 말자. 비용함수는 ${\theta}_{0}$ 와 ${\theta}_{1}$를 최소화하기 위한 것이었다. Cost Function(비용함수) $J({\theta}_{0}, {\theta}_{1})$은 다음과 같다.

Cost Function은 Squared error function이라고 불리기도 한다. Squared error function은 가장 통상적으로 Linear Regression에서 사용되는 방법이다. 우리가 계속 얘기했던 방법이 대부분의 선형 회귀 문제에서 가장 합리적인 방법이다.

지금까지 우리는 비용함수의 수학적인 정의에 대해서 알아보았다.

Cost Function을 최소화 하기

과정

예제를 통해 비용함수가 무슨 일을 하고 왜 우리가 사용해야 하는지 직관적으로 알아보겠다.
우리는 자룔르 일직선에 맞추고 싶어서 hypothesis를 $h_{\theta}(x) = {\theta}_0 + {\theta}_1x$이라고 정의했고, Parameters는 ${\theta}_0, {\theta}_1$, Cost Function은 $J({\theta}_{0}, {\theta}_{1}) = \frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2$로 정의했다. 목표는 $J({\theta}_{0}, {\theta}_{1})$을 최소화 하기 위해 ${\theta}_{0}, {\theta}_{1}$를 조정하는 것이다.

$h_{\theta}(x)$는 $x$의 함수이다. $J({\theta}_{1})$ 는 ${\theta}_{1}$에 대한 함수이다. $h_{\theta}(x)$와 $J({\theta}_{1})$의 계산과정을 통해 최소화 방법을 알아보자.

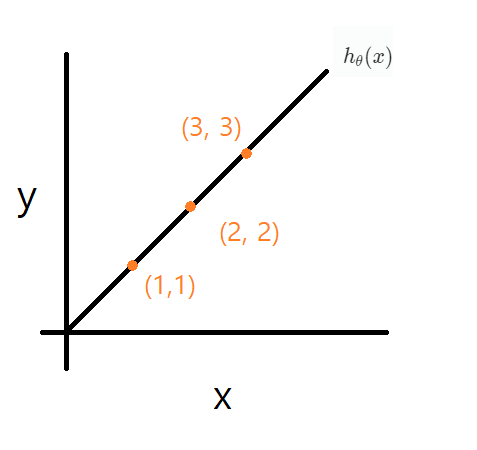
위와 같이 (1, 1), (2, 2), (3, 3)을 지나는 직선인 $h_{\theta}(x)$가 있다고 가정하자.
${\theta}_0 = 0$으로 고정한다.

${\theta}_1 = 1$ 일 때, $J({\theta}_{1})$에 (1, 1), (2, 2), (3, 3)을 지나는 직선인 $h_{\theta}(x)$를 대입하면,

이 된다! 즉, $J(1) = 0$이 된다.

${\theta}_1 = 0.5$ 일 때, $J({\theta}_{1})$에 (1, 1), (2, 2), (3, 3)을 지나는 직선인 $h_{\theta}(x)$를 대입하면,

가 되고, $J(0.5)$는 $0.68$ 정도임을 알 수 있다.

${\theta}_1 = 0$ 일 때, $J({\theta}_{1})$에 (1, 1), (2, 2), (3, 3)을 지나는 직선인 $h_{\theta}(x)$를 대입하면 $J(0)$는 $0.23$ 정도 임을 알 수 있다.

많은 범위를 계산 하다 보면, 우리는 아래와 같은 $J({\theta}_{1})$를 얻을 수 있다.

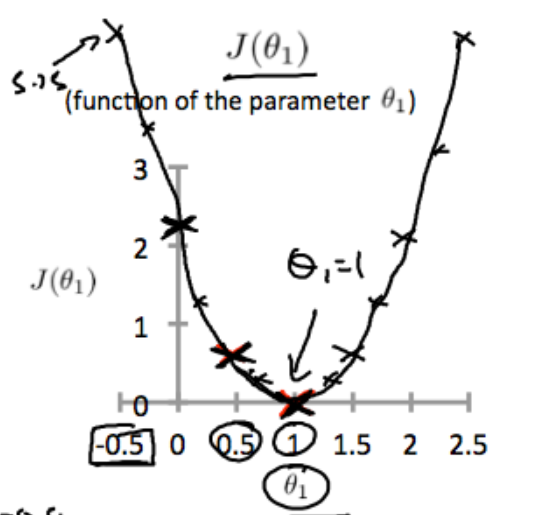
이 과정이 갖는 의미

${\theta}_{1} = 1$일 때, $J({\theta}_{1}) = 0$이고, 이는 아래 그림에서 $h_{\theta}(x)$이 하늘색 직선으로 대응,
${\theta}_{0.5} = 0.68..$일 때, $J({\theta}_{1}) = 0$이고, 이는 아래 그림에서 $h_{\theta}(x)$이 핑크색 직선으로 대응된다.

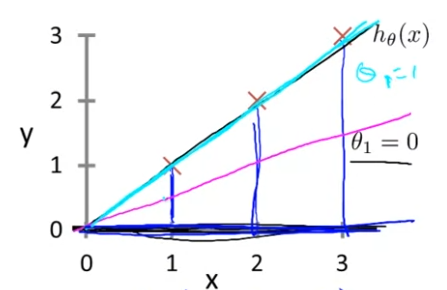
우리의 목적은 $J({\theta}_{0}, {\theta}_{1})$을 최소화하는 것이라고 하였다. 지금까지, 가장 최선은 ${\theta}_{1} = 1$일 때 $J({\theta}_{1}) = 0$이므로 ${\theta}_{1} = 1$일 때이다.
또, 가만 생각해보면, 당연하게도, 데이터셋에 완벽하게 일치하는 직선은 ${\theta}_{1} = 1$이다.(데이터셋에 딱 맞을 때의 ${\theta}_{1}$의 값이 $1$이었으므로.)
이게 바로 Cost Function의 최솟값을 찾아야 하는 이유가 된다.

Cost Function이 최소일 때, 자료에 잘 맞는 직선을 찾는 것과 같기 때문이다.

이번 예시에선 좀 더 이해하기 쉽게 하도록 ${\theta}_0 = 0$으로 고정하여 알고리즘을 간소화 했지만, 이제 고정하지 않고 두 Parameter가 바뀌며 이루어내는 비용함수를 시각화 해보자.

${\theta}_{0}, {\theta}_{1}$이 모두 가변적인 $J({\theta}_{0}, {\theta}_{1})$

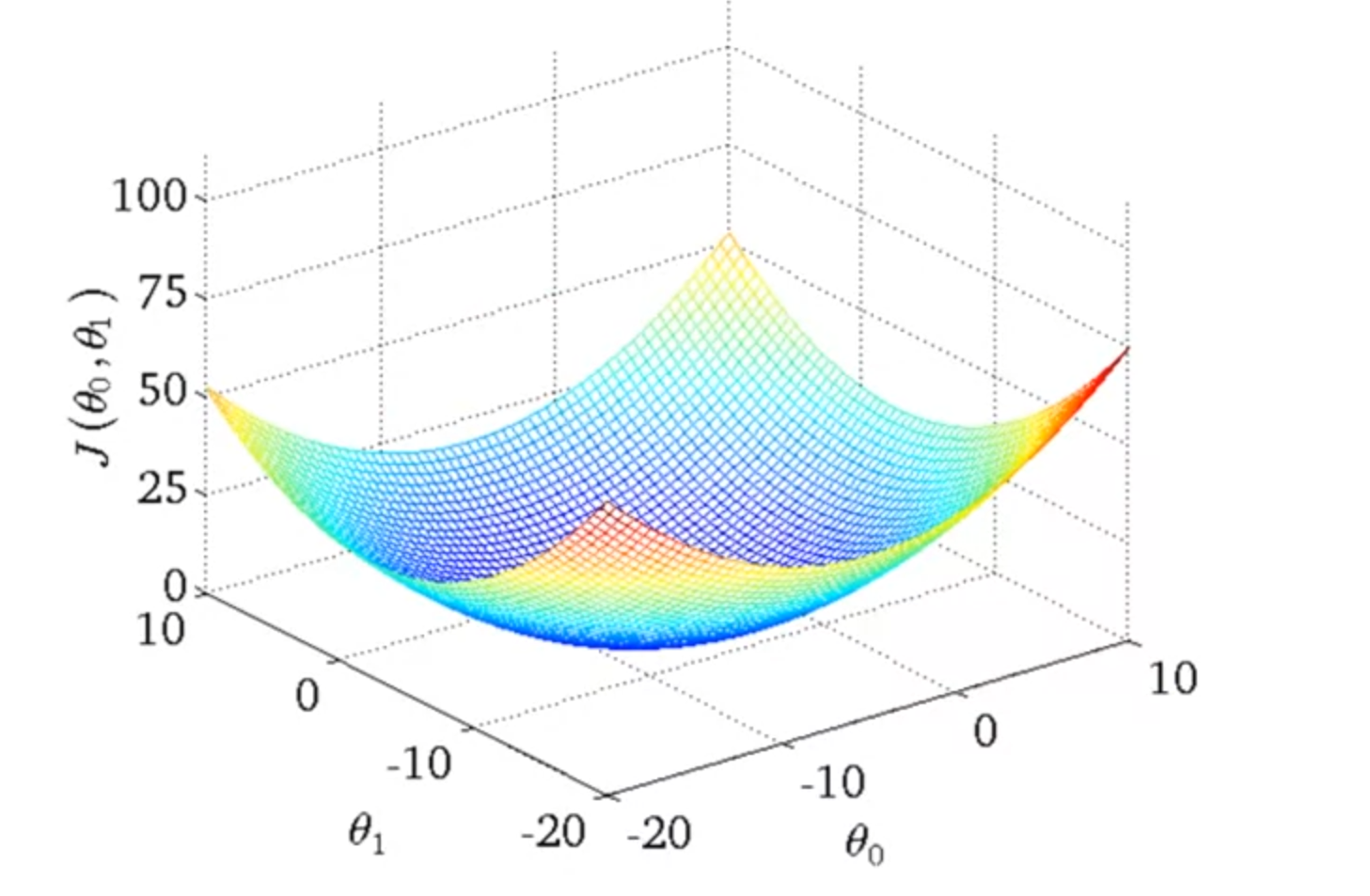
어느 데이터셋에 대하여, $J({\theta}_{0}, {\theta}_{1})$은 다음과 같은 그래프를 보인다. 이를 등고선 그래프(contour plot)으로 나타내면 아래 그림과 같다.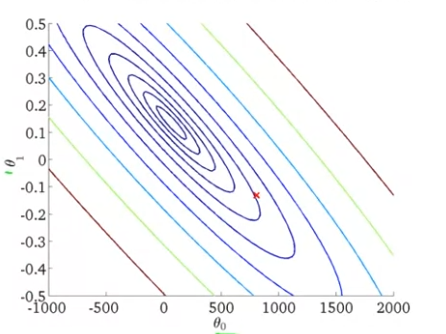
위 그래프에서 빨간 점은 $(800, -0.15)$를 가리킨다. ${\theta}_{0} = 800$이라는 것은, 수직축을 지나는 값이 대략 800이라는 것이다. 그리고 경사는 약 -0.15가 된다. $({\theta}_{0}, {\theta}_{1}) = (800, -0.15)$일 때의 $h_{\theta}(x)$에 비교해서 보자.

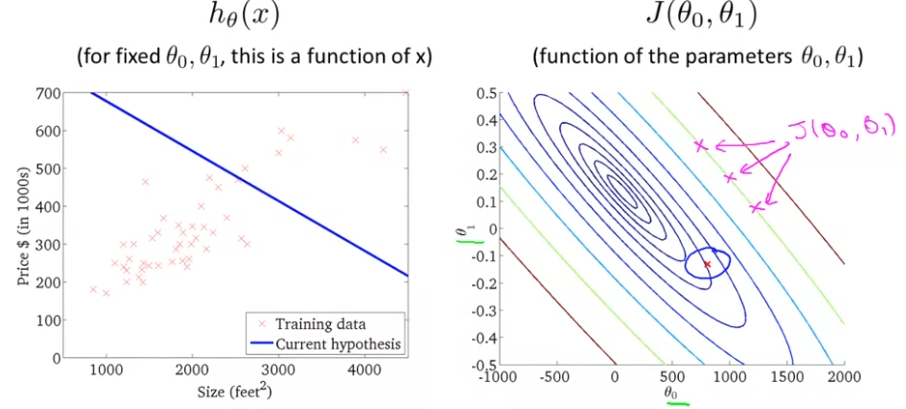
이는 ${\theta}_{0}, {\theta}_{1}$에 대해서 전혀 비슷한 형태를 보이고 있지 않는다. 최소값에 꽤 멀리 떨어져 있고, 높은 비용을 보이고 있다.

이번엔 $({\theta}_{0}, {\theta}_{1}) = (360, 0)$일 때의 $J({\theta}_{0}, {\theta}_{1})$와 $h_{\theta}(x)$를 살펴보자.

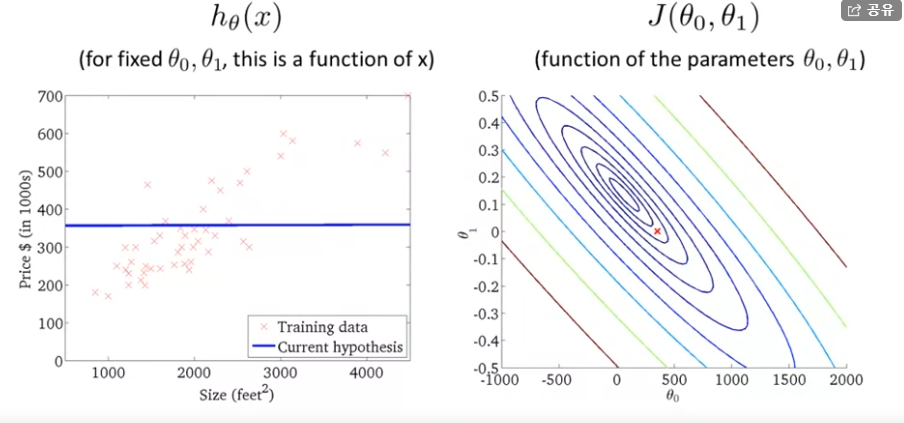
가설은 이렇게 납작한 직선을 보이고 있다. h(x) = 360 + 0 * x 이니 뭐 당연하긴 하지만 말이다.

이번엔 $({\theta}_{0}, {\theta}_{1})$가 최솟값에 가까운 상황을 보자.

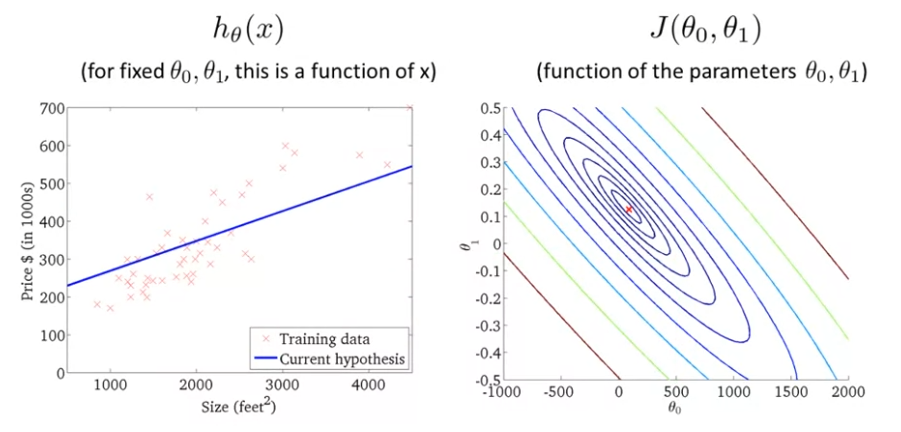
좀 전까지의 예시들은 $({\theta}_{0}, {\theta}_{1})$의 값에 따른 $J({\theta}_{0}, {\theta}_{1})$이 최솟값에 가깝지 않았지만, 이번엔 등고선의 가장 중앙 부분에 위치해 있어서 최솟값에 가깝다.또, 가설 자료랑 거의 비슷한, 꽤 비슷한 값이다! 여기서 오차의 제곱은 가설과 훈련집합들의 거리의 제곱값이라는 것이다. 이는 최소값과 거의 비슷한 값이다.

그래서 오늘 강의에서 더 효과적인 알고리즘이 무엇인지 알았다. 또, ${\theta}_{0}와 {\theta}_{1}, J({\theta}_{0}, {\theta}_{1})$을 구하는 법을 알았다. 이젠 더 복잡한 예시에 대해 볼 것이다. 더 많은 parameter와 고차원 레벨을 다루게 되는데 ㅇ이젠 우리가 직접 그리기 어려워지고, 시각화 하기도 어렵다. 하지만 결국 해야할 일은 똑같다. ${\theta}_{0}와 {\theta}_{1}$을 찾는 것이다. 위대한 그들은 $J({\theta}_{0}, {\theta}_{1})$을 최소화 하는 ${\theta}_{0}와 {\theta}_{1}$을 쉽게 찾는 알고리즘을 고안해냈다. 이제 그 알고리즘을 배워보고자 한다. ⭐넥스트 레벨⭐로 가보자!