[Machine Learning] Gradient Descent Algorithm

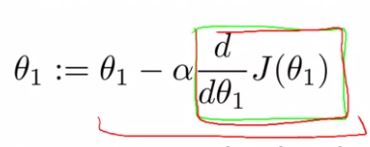
Gradient Descent

기울기 하강은 기계학습의 모든 곳에서 사용되고 있다. 선형 회귀에서만 사용되는 알고리즘이 아니다. 이 강의의 끝 쯤에 우리는 다른 함수들의 최솟값을 구하기 위해 기울기 하강 알고리즘을 사용할 것이다.

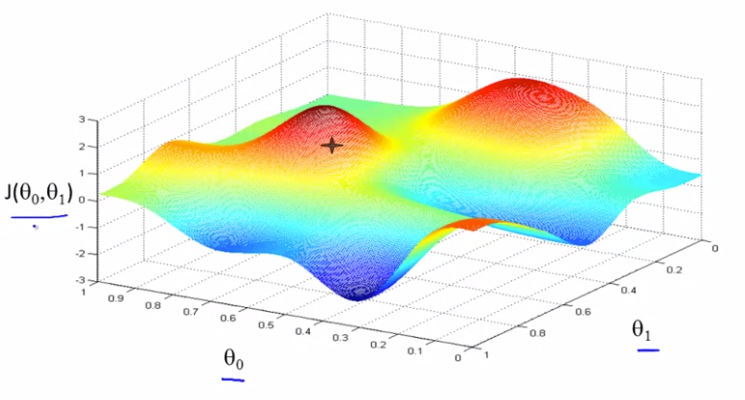
위 같은 비용함수를 예시로 사용하고자 한다.
여기 문제 조건이 있다. 선형회귀의 비용함수 $J({\theta}_{0}, {\theta}_{1})$이 있다고 가정하자. 그리고 $J({\theta}_{0}, {\theta}_{1})$을 최소화 하는 ${\theta}_{0}$와 ${\theta}_{1}$을 찾길 원한다. 기울기 하강은 ${\theta}_{0}, ..., {\theta}_{n}$까지의 범위에 적용이 가능하지만, 공식을 쉽게 증명하기 위해 ${\theta}_{0}$와 ${\theta}_{1}$만 다루고자 한다.

Gradient Descent Algorithm은 다음과 같다.

1. $α$는 훈련비율(number of learning rate)이다.
   우리가 언덕을 내려가기 위해 얼마나 큰 걸음을 걸어야 하는지를 말한다. α이 크면, 큰 보폭으로 언덕을 내려가고, 가파른 하강이 될 것이다. 얼마나 많은 값이 변하는가에 대한 변수이다.
2. $\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$는 미분계수이다.
3. :=는 assignment를 뜻한다.
4. 여기서 주의해야 할 점은 Simultaneous update를 꼭! 지켜야한다는 것이다.
   
   꼭, 동시에 ${\theta}_{0}$와 ${\theta}_{1}$를 바꿔야 한다. 아래처럼 먼저 ${\theta}_{0}$를 계산하고, 이를 ${\theta}_{1}$ 계산에 대입하는 방법을 써선 안된다.
   

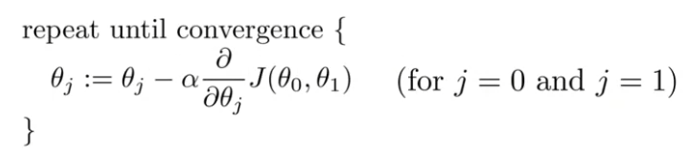
위 식에서 $α$는 훈련비율(number of learning rate)이라고 말했고, $\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$는 미분계수라고 얘기했다. 이번엔 두 용어의 개념을 설명하고, 같이 사용했을 때 어떤 변화가 있는지 얘기해보려고 한다.

$\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$ 면밀하게 살펴보기

😚 들어가기 전에! 양수미분계수와 음수 미분계수의 정확한 정의

양수 미분계수는 해당 값이 0보다 크거나 같을 수 있고,
음수 미분계수는 해당 값이 0보다 작거나 같을 수 있다.

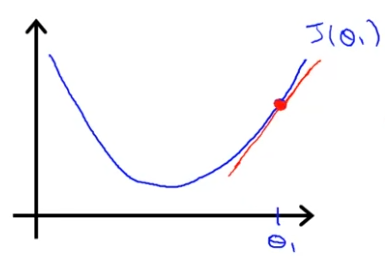
다음과 같은 $J({\theta}_{1})$이 있다고 가정하자.

현재 점에서 기울기가 양수이므로 $\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$가 양수임을 알 수 있고, 양수 미분계수임을 또한 알 수 있다.
${\theta}_{1} := {\theta}_{1} - α*$ ( positive number )가 된다.

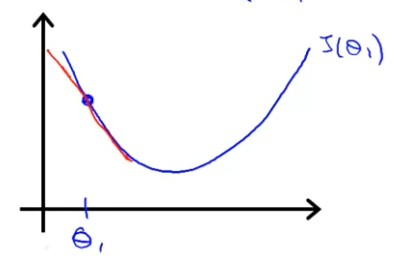
이번엔 점을 옮겨 다음과 같은 상황의 $J({\theta}_{1})$이 있다고 가정하자.
(위에 있는 $J({\theta}_{1})$과 같은 그림이다.)

현재 점에선 기울기가 음수이므로, 이 함수를 음수 미분계수라고 하자.이제 ${\theta}_{1} := {\theta}_{1} - α*$ ( negative number )다.

훈련비율 $α$ 면밀하게 살펴보기

이번엔 $α$가 의미하는 비율의 의미를 살펴보자.

여기 기울기 하강 공식이 있다. 이제부터 $α$값이 너무 작거나 크다면 어떻게 되는지 살펴보자.

아래 그림과 같이 데이터가 멀리 있을 때, $α$가 너무 작다면, 최솟값에 도달할 때까지 정말 느릴 것이다.

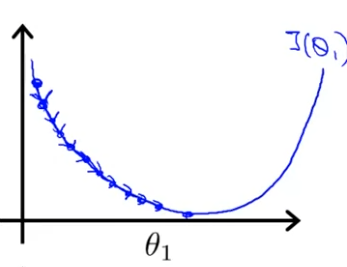
또, 아래 그림과 같이 데이터가 최솟값과 가깝게 있을 때, $α$가 너무 크다면, 최솟값에 도달하기도 어렵고 방향을 전환하는 것조차 실패할 수 있다.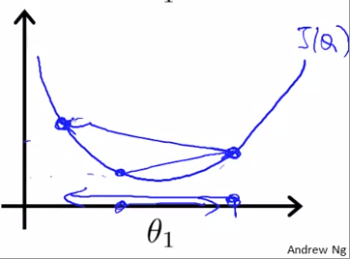

이미 ${\theta}_{1}$이 최소일 때?

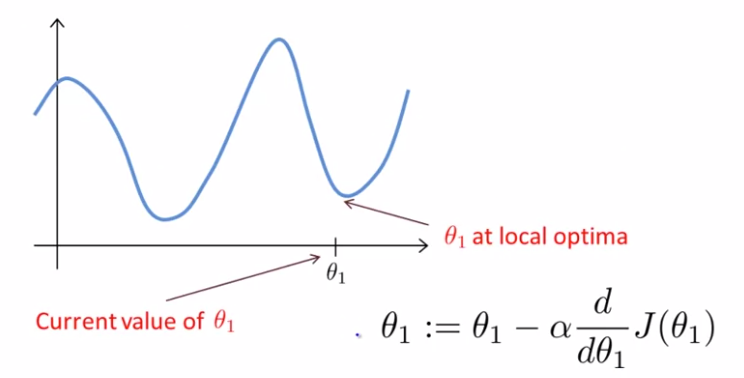
위와 같은 상황이 있다고 가정하자. ${\theta}_{1}$는 이미 local minimum/local optima에 있다. local optima이면 미분계수는 0이다. 이를 ${\theta}_{1} := {\theta}_{1} - α\frac{∂}{∂{\theta_j}}J( {\theta}_{1})$에 대입하면 ${\theta}_{1} := {\theta}_{1}$이므로 하강 기울기는 파라미터에 영향을 받지 않고, local optima가 유지된다.

훈련비율 $α$가 고정일 때

훈련비율 $α$가 고정이면, Gradient Descent는 local minimum에 수렴(converge)될 수 있다. 다음 예제를 보며 이해해보자.

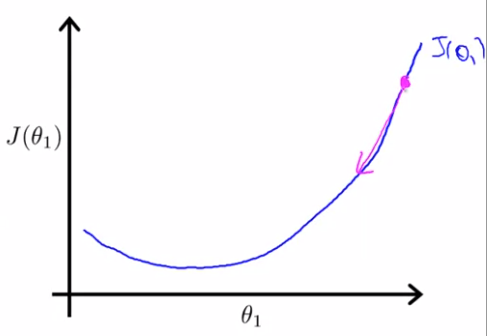
먼저 위 같은 $J({\theta}_{1})$이 있을 때, ${\theta}_{1}$의 값이 핑크색으로 표시되어 있는 이 점과 같다고 하자. 이 점에서 기울기는 매우 가파르기 때문에, 핑크색으로 표시된 기울기만큼 움직이게 된다. 다음 Gradient Descent Step으로 넘어가서 이제 초록색 지점으로 이동하게 된다고 하자.

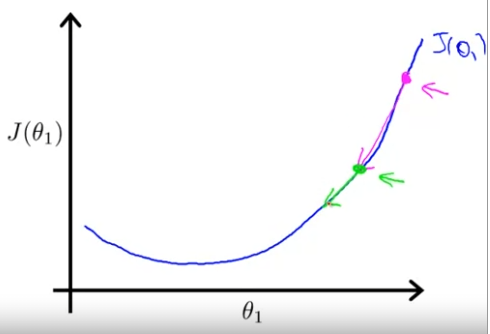
초록색 지점에서의 기울기는 초록색으로 표시된 정도이고, 핑크색보다 덜 가파른 것을 볼 수 있다. 최솟값에 가까울 수록 기울기는 점점 작아지기 때문에 당연한 결과다.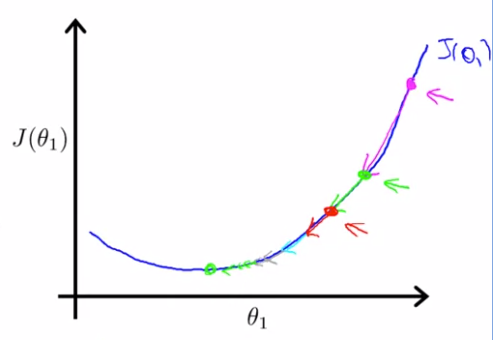
이런식으로 계속 진행하게 되면, Gradient Descent를 진행하면서 최솟값에 가까워 질수록 점점 작은 step으로 이동하게 되고, 이 이유는, 지역 최솟값의 미분 계수는 0이기 때문이다. 따라서 지역 최솟값에 가까워질수록 미분 계수값은 작아지게 되고 Gradient Descent는 더 작아진다. 따라서 훈련비율 $α$를 가변적으로 할 필요가 없다.