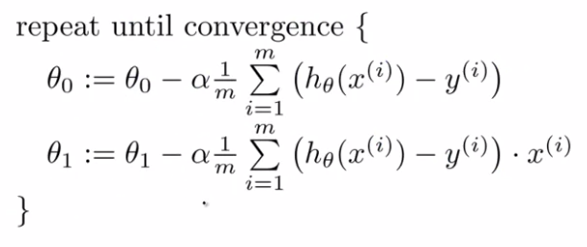[Machine Learning] Gradient Descent For Linear Regression

이번에는 비용함수와 Gradient Descent를 함꼐 사용해서 선형회귀를 위한 알고리즘을 구하거나 우리의 data의 일차함수를 구해보도록 한다. 왼쪽은 앞에서 배웠던 Gradient Descent Algorithm과 Linear Regression Model이 있다. Linear Hypothesis인 $h_{\theta}(x) = {\theta}_0 + {\theta}_1x$도 있고, Cost Function (Squared Error Cost Function)인 $J({\theta}) = \frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2$도 보인다.

이제 우리가 하려는 것은 Gradient Descent를 이용해 Cost Function을 최소화 하려는 것이다. $\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$에 Linear Regression Model 공식을 대입해보자.

$\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1}) = \frac{∂}{∂{\theta_j}} * \frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2 = \frac{∂}{∂{\theta_j}}\frac{1}{2m}{\sum\limits_{i=1}^m}({\theta}_0 +{\theta}_1x^{(i)}-y^{(i)})^2$

또, j=0 또는 j=1일 때의 미분계수 $\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1})$는 다음과 같이 나타낼 수 있다.

$j=0:\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1}) =\frac{1}{m}{\sum\limits_{i=1}^m}(h_{\theta}(x^{(i)}) - y^{(i)})$

$j=1:\frac{∂}{∂{\theta_j}}J({\theta}_{0}, {\theta}_{1}) =\frac{1}{m}{\sum\limits_{i=1}^m}(h_{\theta}(x^{(i)}) - y^{(i)}) * x^{(i)}$

이 정의를 가지고 Gradient Descent Algorithm을 다음과 같이 정의할 수 있다.

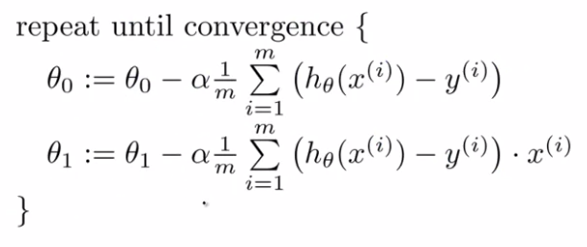
꼭 ${\theta}_{0}, {\theta}_{1}$를 동시에 변경해야 한다!

이것이 우리의 Linear Regression Algorithm이 된다.

Batch Gradient Descent

Batch는 training examples에서 모든 Gradient Descent의 단계를 포함한 것을 말한다. Gradient Descent에서 미분 계수를 계산할 때, 우리는 sum으로 m개의 training examples들을 더한다. 그래서 Batch Gradient Descent는 모든 Training examples의 전체 집단을 나타내는 의미이다.