[Machine Learning] Multiple features

이번에는 더 강력한 새로운 Linear Regression을 배워볼 것이다. 우리가 전에 배웠던 Linear Regression은 다음과 같다.

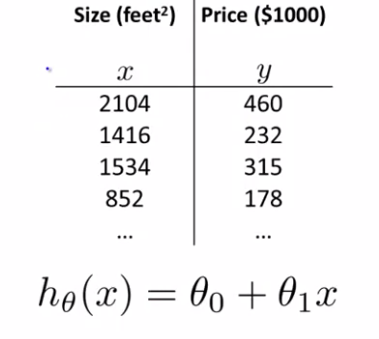
이렇게 feature이 하나고(여기선 Size)였지만 이제 feature을 여러개 갖는 형태가 될 수 있음도 생각해볼 수 있다.

Multiple features

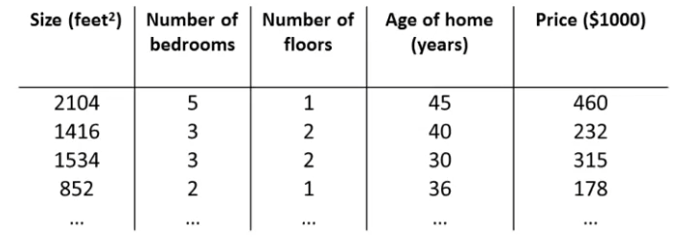
여기서 우리는 4개의 feature을 확인할 수 있다. Noation을 정리해보자.

Notation
$n$ = number of features. (feature의 갯수)
$x^{(i)}$ = input (features) of $i^{th}$ training examples. (입력 feature)
$x_j^{(i)}$ = value of feature $j$ in $i^{th}$ training examples. (입력 feature의 feature 인덱스를 포함해 입력 feature을 나타낸다.)

위 예제에서 $x^{(2)} =\begin{bmatrix}1416\\3\\2\\40\end{bmatrix}$이 된다. 왜냐면 2번째 집의 가격을 결정하는 요소이기 때문이다. 그리고 여기 변수명을 보면 $x^{(2)}$, 즉, $2$라고 되어 있는데, 이는 2번째 인덱스이기 때문이다. 여기서 feature은 4개이므로, $x_3^{(2)} = 2$라고 나타낼 수 있다.

hypothesis

앞서 우리는 $h_{\theta}(x) = {\theta}_0 + {\theta}_1x$ 임을 확인했다. 이는 $x$가 단일 feature일 때 성립한다. 하지만 이제 여러개의 feature이 있으므로 단순하게 표현하지 않을 것이다. 사실 가만히 살펴보면 선형 회귀 추론의 형태를 하고 있는 것을 알 수 있다. 따라서 n개의 feature에 대해 hypothesis는 다음과 같이 나타낼 수 있다.

$h_{\theta}(x) = {\theta}_0 + {\theta}_1x + {\theta}_2x^2 +... + {\theta}_nx^n = {\theta}^TX$

단, $X=\begin{bmatrix}X_0\\X_1\\...\\X_n\end{bmatrix} ∈ \mathbb R^{n+1}, \theta=\begin{bmatrix}\theta_0\\\theta_1\\...\\\theta_n\end{bmatrix} ∈ \mathbb R^{n+1}.$

이는 Multivariate linear Regression이라고 부른다. 여러 개의 feature혹은 변수를 표현하는 말이다.