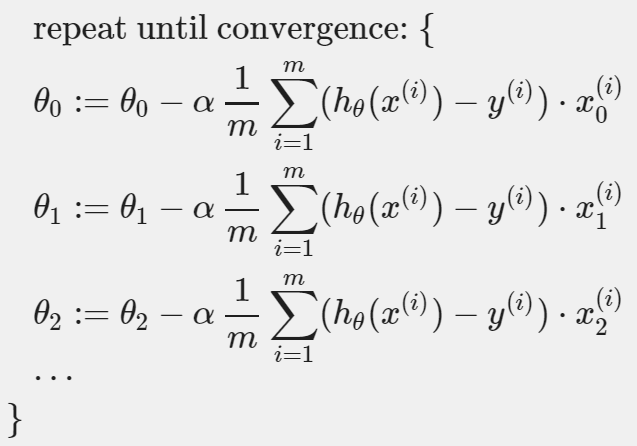[Machine Learning] Gradient Descent for Multiple Variables

이번에는 Linear Regression을 위한 Gradient Descent를 여러 변수가 있을 때 어떻게 쓰는지 알아보려고 한다.

Hypothesis : $h_{\theta}(x) = {\theta}_0 + {\theta}_1x + {\theta}_2x^2 +... + {\theta}_nx^n = {\theta}^TX$
Parameters : ${\theta}_0, {\theta}_1, {\theta}_2, ..., {\theta}_n.$ 하지만, 우리는 이것을 그냥 ${\theta} (n+1 dim.)$ 라고만 표현하기로 하자.
Cost Function : $J({\theta}_0, {\theta}_1, ..., {\theta}_n) = J(\theta)=\frac{1}{2m}{\sum\limits_{i=1}^m}(h_{\theta}(x) - y)^2$
Gradient Descent : $Repeat$ { $\theta_j := \theta_j - α\frac{∂}{∂{\theta_j}}J({\theta}_{0}, ... ,{\theta}_{n}) = \theta_j - α\frac{∂}{∂{\theta_j}}J({\theta})$ } (simultaneously update for every $j=0,...,n$)

Gradient Descent에 Cost Function을 대입한 이전의 Gradient Descent는 다음과 같았다.

하지만 $n$이 $1$보다 같거나 클 때는 다음과 같다.

그리고, 이를 다음과 같이 쓸 수도 있다.