[Machine Learning] Gradient Descent in Practice - Feature Scaling, Learning Rate

Gradient Descent

${\theta}_{j} := {\theta}_{j} - α\frac{∂}{∂{\theta_j}}J({\theta})$

이번엔 Gradient Descent를 잘 활용할 수 있는 몇 가지 방법을 알아보려고 한다.

Feature Scaling

💡 Idea

여러 개의 feature가 있고 feature의 단위 크기가 비슷하다면(서로 다른 feature라도 범위가 대략적으로 같다면), gradient descent는 더 빨리 수렴할 수 있다.

만약,

라면, cost function $J(\theta)$는 다음과 같이 그릴 수 있다.

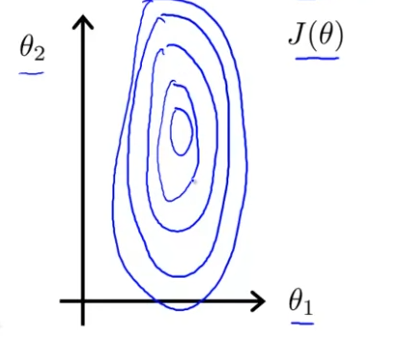
$x_1$의 범위가 $x_2$보다 훨씬 크기 때문에, 2000:5의 비율이 나오고, 이렇게 뾰족한 모양의 등고선이 그려진다. 여기에 gradient descent를 적용하면 gradient는 오랜 시간동안 앞 뒤로 진행하며 아주 많은 시간이 지난 후에 마침내 최솟값에 도달하게 될 것이다. 아래 그림처럼 말이다.

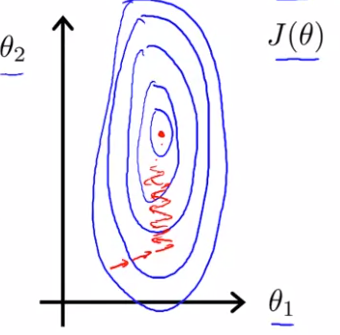
얇고 긴 등고선이라면, 그리고 극단적으로 뾰족하다면 gradient descent는 훨씬 더 많은 시간을 소요하고, 구불구불하게 가다가, 오랜 시간이 지나서야 최솟값을 찾을 수 있다.

이 때 유용한 방법이 feature을 조절하는 것이다.

이렇게 되면 $0≤x_1≤1, 0≤x_2≤1$이다. 이 $x_1$, $x_2$ 값으로 $J(\theta)$를 그리면 다음과 같다.

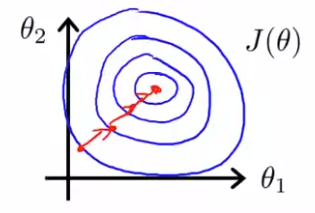
cost function에 gradient descent를 하면, 정확하게 최솟값을 찾을 수 있다. 난해한 경로로 구불구불하게 가지 않을 수 있다.

보통은 feature scaling을 하면 feature이 $-1≤x_i≤1$에 근사하게 있기를 바란다. 꼭 -1과 1사이에 있어야 하는 건 아니다. 근사한 정도만 되면 된다. $0≤x_i≤3$도 괜찮고, $-2≤x_i≤0.5$도 괜찮다.

하지만, 범위가 $-100≤x_i≤100$ 정도면 이는 $-1≤x_i≤1$와 많이 다르므로 좋은 feature가 아니다. 또 $-0.00001≤x_i≤0.00001$인 경우에도 $-1≤x_i≤1$과 근사하지 않기 때문에 feature을 조절해야 한다.

Mean Normalization

feature scaling을 할 때 최댓값으로 나누고 보통 mean normalization을 할 수 있다. mean normalization은 feature의 평균이 대략적으로 0이 되게 하기 위해 $x_i$를 $x_i-μ_i$로 교체하는 것이다. 단, $x_0=1$이면 평균이 0이 될 수 없기 때문에 $x_0=1$를 허용하지 않는다.

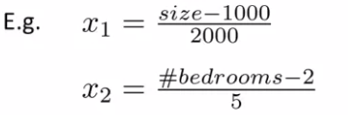
위와 같은 과정을 거치면,

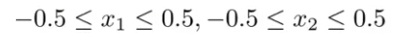
다음과 같은 범위를 얻을 수 있다.

feature scaling + mean normalization

따라서 다음과 같이 사용되는 것이 일반적이다.

$x_i := \frac{x_i - μ_i}{s_i}$

여기서 $μ_i$는 training set에 있는 $x_i$의 평균 값이다. $s_i$는 범위가 될 수 있고, 편차를 알고 있다면 표준편차로 써도 된다. 하지만 최대값-최솟값도 좋다.

---

Gradient Descent는 다음과 같이 나타낸다.

이번엔 Debugging을 통해 gradient descent를 더 잘 돌아가게 해보자.
그리고 lelarning rate $α$를 잘 선택하는 방법도 알아볼 것이다.

Gradient Descent의 수렴 판단

📃 Automatic Convergence Test

Automatic Convergence Test을 이용하면 Gradient Descent의 수렴 판단을 할 수 있다. Gradient Descent가 언제 수렴하는지 판단하는 기준은 Cost Function $J(\theta)$가 $10^{-3}$(임계값)보다 작게 감소할 때 수렴한다고 판단한다. 하지만 이런 임계값을 정하는 것도 쉽지 않다. 그래서 수렴을 확인하기 위해 실제로 그래프를 그리는 게 좋다. automatic convergence test는 잘 쓰지 않는다.

📉 그래프

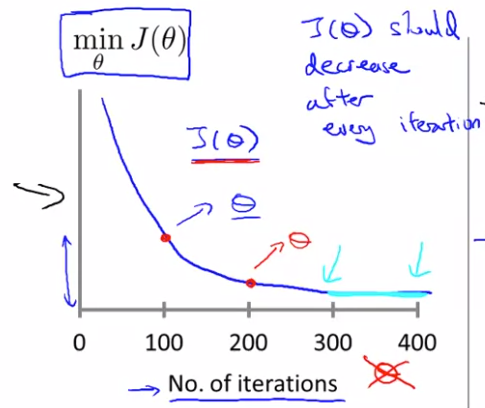
Gradient Descent의 목적은 cost function이 최소화 되는 $\theta$를 찾는 것이다. 이번에 x축은 Gradient Descent를 반복한 반복 횟수이다. 그래프를 보면 알겠지만, 매 iteration(반복) 때마다, const function $J(\theta)$는 감소한다.
300~ 400저옫를 보면, iteration 횟수를 올라도 $J(\theta)$의 값이 바뀌지 않는 것처럼 보이고, 400이 넘으면 수렴한다고 볼 수 있다.

Learning Rate $α$

$α$가 너무 작으면 아주 천천히 수렴한다.
$α$가 너무 크면 모든 iteration에서도 줄어들지 않을 수 있다. 즉, 수렴하지 않거나 아주 천천히 수렴하게 될 수 있다.

따라서 $α$를 선택할 때,

..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ... 위와 같은 방법으로(0.001에서 3배, 10배 ...) 작은 것부터 시작하여 점점 증가 시켜 시험해보고, 가능한 가장 작은 값과 가장 큰 값을 찾는다.