From Word Embeddings To Document Distances

Word2Vec을 활용하여 문서 간의 거리를 측정하는 Word Mover's Distance를 소개하는 논문입니다.

[Abstract]

해당 논문에서는 Word Mover's Distance(WMD)라는 명칭의 문서 간 거리측정 지표를 소개합니다. WMD는 두 문서 간의 거리를 한 문서의 embedded 단어들이 다른 문서의 embedded 단어로 이동할 때 필요한 거리의 최소값으로 정의됩니다. 이는 transportation problem의 Earth Mover's Distance의 예시로 볼 수도 있습니다.

1. Introduction

문서 간의 거리를 제대로 표현하는 것은 다양한 분야에서 활용됩니다. 문서를 표현하는 대표적인 2가지 방법으로 Bag of words(BOW)를 활용하는 것과 TF-IDF를 활용하는 것이 있습니다. 두 방법 모두 near-orthogonaily(표현되는 벡터들 간 관계가 대부분 orthogonal)한 특성이 있기 때문에 문서 간의 거리를 표현하기에는 부족함이 있었습니다. 또 다른 문제점은 개별 단어들 간의 거리를 제대로 잡아내지 못한다는 점입니다.
'The President greets the press in Chicago' 와 'Obama speaks to the media in Illinois'는 공통된 단어는 없지만 의미적으로 매우 유사합니다. BOW는 두 문장이 의미적으로 유사하다는 것을 잡아낼 수 없습니다.
문서를 latent low-dimensional representation으로 표현하는 방법은 다양합니다. Latent Semantic Indexing(LSI), Latent Dirichlet Allocation(LDA)는 확률적으로 유사한 단어들을 topic으로 묶고, 문서를 이러한 topic들의 분포로 표현합니다. 이러한 방법들이 BOW보다는 document representation에 있어서 조금 더 나을 수는 있지만 거리 기반 task에서는 실질적으로 BOW보다 나은 결과를 보여주지는 못했습니다.
해당 논문에서는 word2vec를 활용하여 문서 간의 거리를 측정하는 metric을 소개합니다. Word Mover's Distance(WMD)는 유사한 단어는 유사한 공간에 위치하고, vector 연산을 통해 단어의 의미정보를 포함할 수 있는 word2vec의 특징을 활용합니다. 해당 논문에서 문서는 embedded words의 weighted point cloud로 간주합니다. 두 문서 A와 B의 거리는 A 문서의 단어들에서부터 B문서의 단어들로 이동하기위해 필요한 거리 총합의 최소값으로 정의합니다.
WMD의 특징은 다음과 같습니다.

• Hyperparameter free
• straight-forward to understand and use
• Interpretable
• Incorporates the knowledge encoded in the word2vec space
• High retrieval accuracy

2. Related Work

두 문서간의 거리를 구하는 방법은 document representation을 학습하는 방법과 관계가 깊습니다.

• Okapi BM25 function
• LDA
• TextTiling
• EMD
• SDA
• faster mSDA
• Componentail Counting Grid merges LDA
• Counting Grid

3. Word2Vec Embedding

Word2Vec 논문 링크 1
Word2Vec 논문 링크 2

4. Word Mover's Distance

n개의 단어에 대해 d차원 벡터로 embedding시킨 d x n word2vec 행렬 X가 있다고 가정합니다. i번째 단어는 X행렬의 i번째 column vector로 표현됩니다. text document를 n차원 벡터인 normalized bag-of-words(nBOW)로 표현한다고 가정합니다. nBOW의 원소는 전체 단어의 개수에서 해당 단어가 등장한 횟수를 비율로 표현한 값입니다.

nBOW representation
vector d를 (n-1) dimensional simplex of word distribution의 point로 생각합니다. 완전히 다른 단어들로 이루어진 2개의 문서는 완전히 다른 simplex에 위치합니다. 그러나 여전히 두 문서는 의미적으로는 유사할 수 있습니다. stop-word를 모두 제거한 후 2개의 nBOW 벡터 d, d'은 실질적인 거리는 가까울 수 있더라도, 공통된 non-zero dinesion이 없기때문에 simplex distance는 커지게 됩니다.

Word travel cost
해당 논문의 목표는 단어 간의 의미적인 유사도를 문서 거리를 측정하는 지표에 녹여내는 것입니다. i 단어와 j 단어의 유클리안 거리인 c(i,j)를 하나의 단어에서 다른 단어로 traveling할 때 필요한 cost로 정의합니다.

Document distance
두 단어의 travel cost는 문서 사이의 거리를 만들어내는 요소입니다.

T는 nBOW vector의 어느정도 값(비율) 만큼 해당 단어에서 다른 단어로 이동할 지 비율(가중치)를 표현하는 행렬을 의미합니다.

Transportation problem
d에서 d'로 이동하는 최소 거리합은 아래의 식을 통해 구할 수 있습니다.

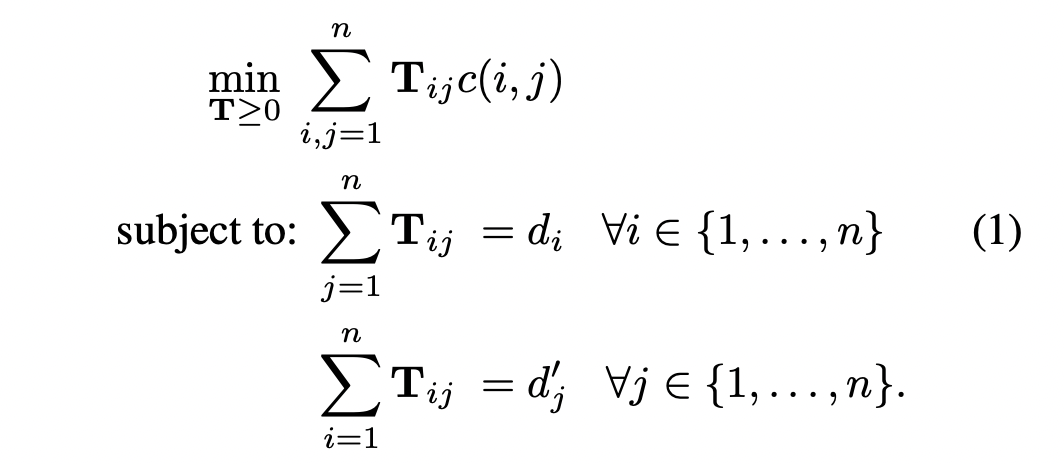
위 식의 최적값은 EMD(earth mover's distance metric)의 특별한 case입니다. EMD와의 관계를 강조하기 위해 도출되는 지표를 Word Mover's Distance(WMD)라고 부릅니다.

Visulization

Figure2 설명 링크

4.1 Fast Distance Computation

WMD 최적화 문제의 평균 시간 복잡도는 문서의 unique word 수가 q일 때 O(p^3logp)입니다. 시간 복잡도를 줄이기 위해 WMD의 lower bounds를 구하는 방법들을 소개합니다.

Word centroid distance
삼각부등식을 활용하여 시간 복잡도가 O(dp)인 lower bound 값인 Word Centroid Distance(WCD)를 구할 수 있습니다. WCD는 각 문서들을 word vector들의 가중평균으로 표현합니다.

Relaxed word moving distance
WCD는 계산속도가 빠른 이점이 있지만 lower bound로서 tight하지 않다는 단점이 있습니다.

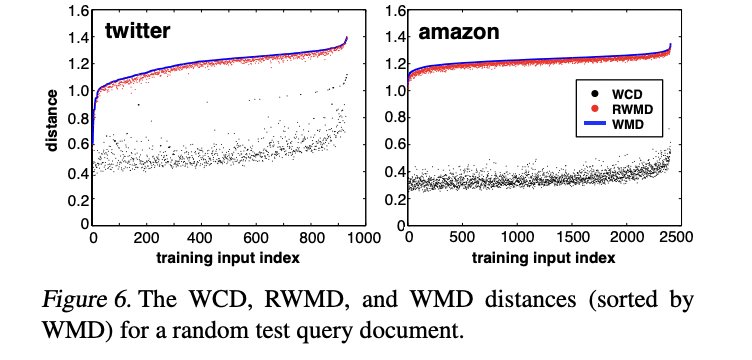
조금 더 tight한 lower bound를 구하는 방법으로 기존 WMD의 제약 조건 중 하나를 제거한 후 구하는 방법을 사용합니다.

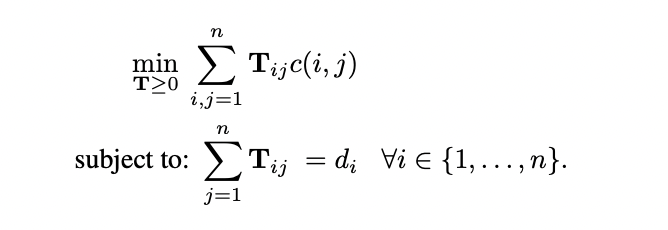
Relaxed WMD(RWMD)는 두 개의 제약 조건 중 하나 씩 제거했을 때의 값을 비교했을 때 큰 값으로 정의합니다.

Prefetch and prune
먼저 문서들을 계산 속도에 이점이 있는 query 문서와의 WCD를 활용하여 오름차순으로 정렬합니다. 오름차순으로 정렬된 첫 k개의 문서에 대해 WMD를 계산합니다. 남은 문서들에 대해서는 RWMD lower bound가 현재 계산된 k개의 WMD 값을 넘는지 확인합니다. 만일 넘는다면 해당 문서는 제거합니다. RWMD는 매우 tight하기 때문에 95%의 문서들이 prune됩니다.

5. Results

5.1 Dataset Description and Setup

8개의 dataset을 활용하여 KNN 분류 성능을 비교합니다.

• BBCSPORT
• TWITTER
• RECIPE
• OHSUMED
• CLASSIC
• REUTERS
• AMAZON
• 20NEWS

비교 대상 알고리즘으로 7개를 활용합니다.

• BOW (bag-of-words)
• TFIDF (term frequency-inverse document frequency)
• BM25 Okapi
• LSI (Latent Semantic Indexing)
• LDA (Latent Dirichlet Allocation)
• mSDA (Marginalized Stacked Denoising Autoencoder)
• CCG (Componential Counting Grid)

5.2 Document classification

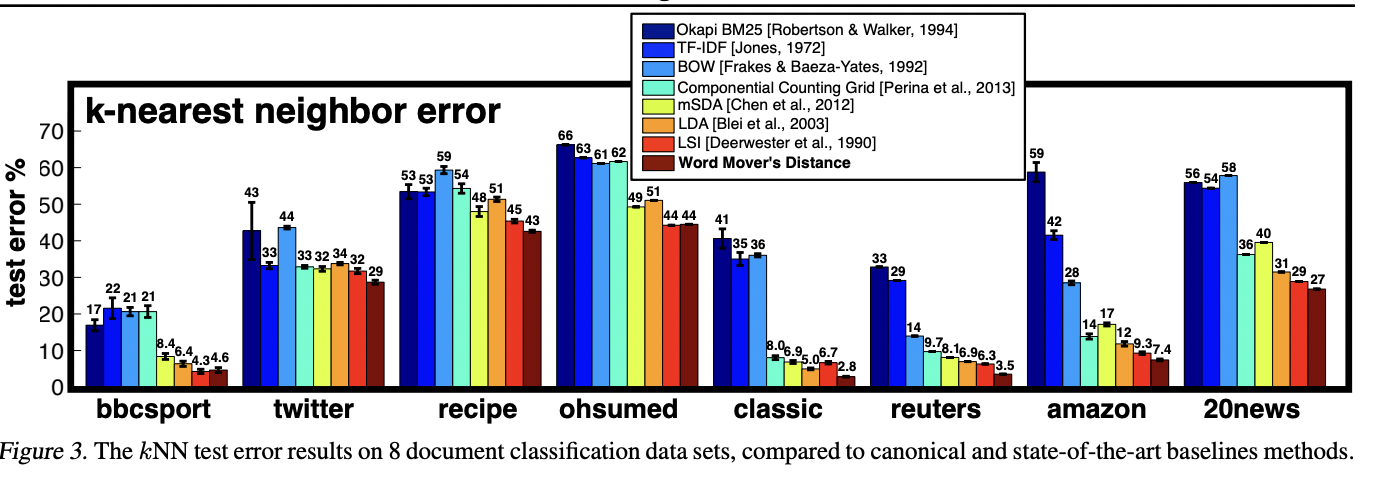
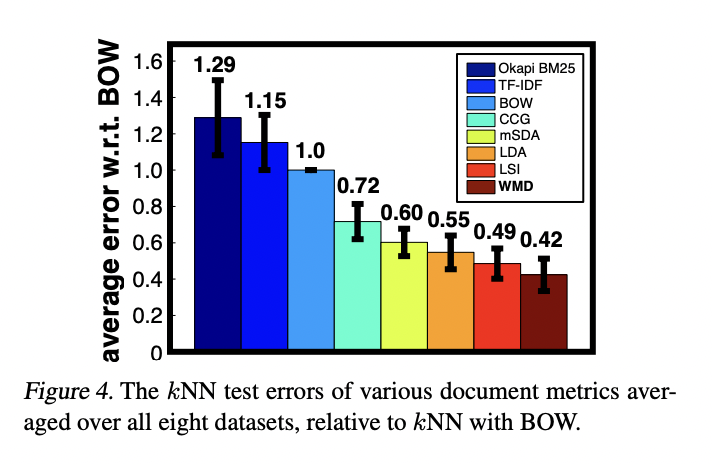
5.3 Word embeddings

WMD는 word embedding 결과에 영향을 받습니다.

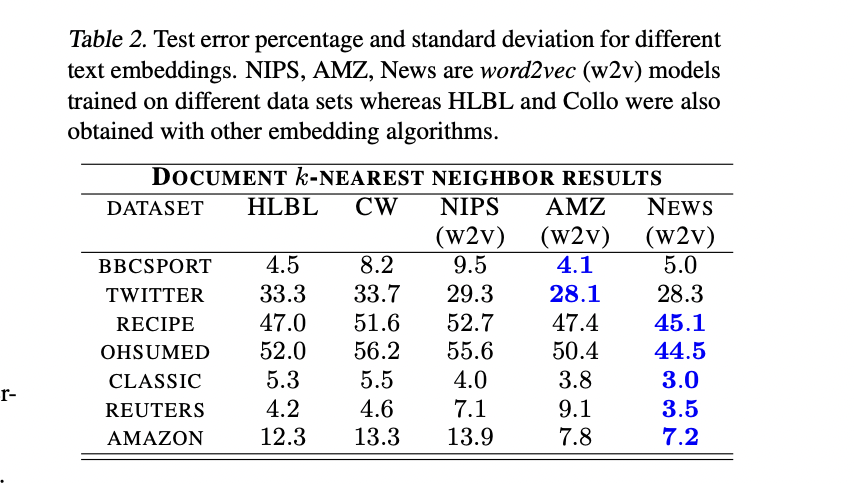
6. Discussion and Conclusion

WMD가 모든 data set에서 다른 방법들에 비해 error rate가 낮은 이유는 무엇이었던 것일까? 해당 논문에서는 질문의 답을 좋은 quality의 word2vec embedding을 사용했기 때문이라고 답합니다. 수십억 개의 단어로부터 학습된 word2vec embedding은 문서의 knowledge를 잡아낼 수 있습니다.
WMD의 매력적인 특징 중 하나는 설명가능하다(interpretability)는 것입니다. 문서간의 거리는 단어들 간의 거리로 나누어 생각할 수 있습니다. 단어들 간의 거리는 시각화할 수 있고 설명하기에 수월합니다.
또 다른 흥미로운 방향은 두 개의 단어가 비슷한 구조의 문서에서 다른 section에 위치한다면 penalty를 추가하여 단어들 사이의 거리를 구하여 문서 구조를 고려할 수 있다는 점입니다.