[PyTorch] Autograd와 Optimizer

MinI0123·2023년 3월 18일

부스트캠프 AI Tech 5기

목록 보기

8/20

Autograd

torch.autograd는 PyTorch의 자동 미분 엔진이다. 역전파 과정에서 필요한 미분 계산을 대신 해줘 신경망 학습을 간단하게 만들어 준다. autograd가 하는 일은 다음과 같다. torch.Tensor.backward는 Tensor autograd functions 중 하나이다.

순전파 단계 : 결과 Tensor 계산, DAG 만들기
역전파 단계 : .grad_fn으로 기울기 계산, 각 Tensor의 .grad에 기울기 축적(accumulate), 연쇄 법칙을 이용해 모든 Tensor에 전파

backward(역전파) 과정에서 기울기를 계산하면 .grad 변수에 단순 저장하는 것이 아니라 이전의 .grad 값에 더해져서 저장된다. 즉 .grad 를 초기화하지 않으면 기울기가 계속 축적됨에 주의해야 한다.

backward 함수

backward 함수는 일반적으로 Vector-Jacobian Product를 구하는 일을 수행한다.

야코비안 행렬 (Jacobian)

야코비안 행렬은 벡터 함수에서 변화도를 나타내는 행렬이다.
Vector-Jacobian Product

위와 같이 어떤 스칼라 함수에 대한 y의 변화도 벡터를 가지고 있는 경우 벡터와 야코비안 행렬의 곱을 사용하면 연쇄 법칙에 따라 스칼라 값에 대한 x의 미분 벡터를 구할 수 있게 된다. backward 함수의 인자 external_grad는 Loss 값을 해당 tensor의 출력 값으로 미분한 값으로 위의 식에서 v벡터가 된다.
Example

import torch

a = torch.tensor([2., 3.], requires_grad = True) # 미분 대상
b = torch.tensor([6., 4.], requires_grad = True) # 미분 대상

Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.]) # 외부 전달 미분 값
Q.backward(external_grad) # 역전파 

print(a.grad) # [36, 81]
print(b.grad) # [-12, -8]

Computational Graph

autograd는 순전파(forward) 과정에서 모든 연산을 기록한 그래프인 Directec Acyclic Graph(DAG)를 생성하여 연산 순서를 저장한다. backward 함수를 호출하는 경우 해당 객체를 root로 DAG의 leaf까지 추적하며 연쇄 법칙을 적용하여 모든 parameter에 대한 기울기를 자동으로 계산한다.

requires_grad
autograd는 requires_grad가 True인 tensor에 대한 연산만 추적한다. 따라서 기울기 계산 및 업데이트가 필요없는 경우 requires_grad를 False로 설정하면 DAG에서 제외할 수 있다. 입력 Tensor중 하나라도 requires_grad = True라면 연산의 결과 Tensor도 requires_grad = True이다.
retain_graph

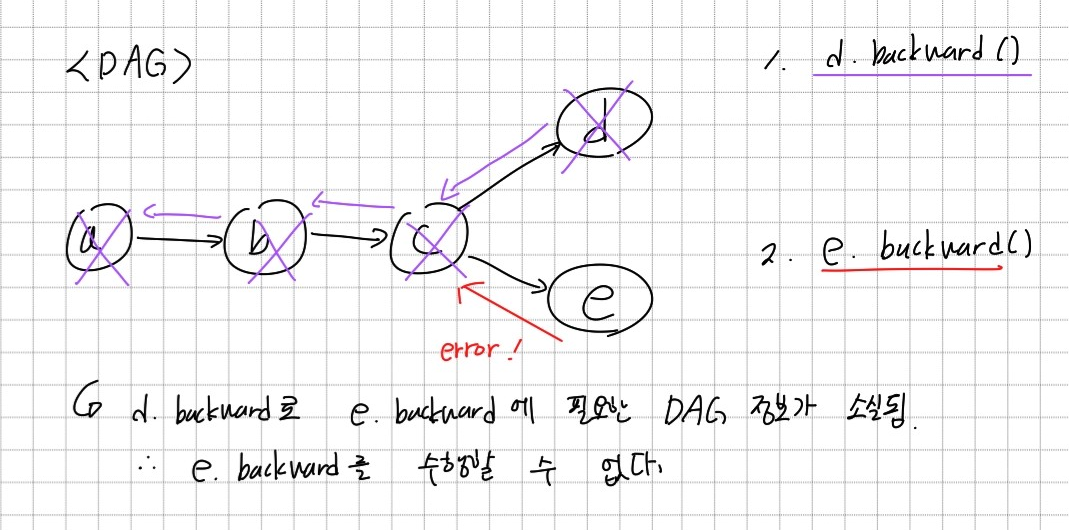
autograd는 메모리를 효율적으로 사용하기 위해서 backward를 수행하고 나면 해당 그래프 정보를 제거한다. 따라서 위와 같은 DAG에서 d에 대해 backward를 수행하고 나면 a → b → c → d의 정보가 그래프에서 사라진다. 이때 e의 backward를 호출하면 그래프의 leaf인 a까지 가는 그래프 정보가 사라졌기 때문에 에러가 발생한다. 이를 방지하기 위해서는 backward 함수에 retain_graph=True를 인자로 주어 backward 연산 후에 그래프 정보를 지우지 않을 것을 명시해줘야 한다.