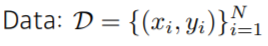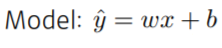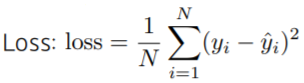02-1. Neural Networks

Neural Network란?

• In Wikipedia...
  
• 시작은 뉴런을 모방했을 지도 몰라도, 요즘에 딥러닝에 사용되는 인공신경망은 다른 형태를 가짐
  
  

Neural Network의 수학적 정의

Neural Networks are function approximators that stack affine transformations followed by nonlinear transformations.

• 연산이 반복해서 이루어짐!

---

Linear Neural Networks

정의

• Data $D$: $N$개의 $x,y$ 순서쌍
  • 
• Model: $x$ -> $\hat{y}$의 mapping을 찾게 해주는 식, 여기서는 선형
  • 
• Loss: (정답 - 추정치) 오차 제곱의 평균 (MSE)
  • 

우리의 목적: Loss 최소화

• $w$와 $b$ 각각을 편미분하여, Loss가 작아지는 방향으로 update
• 

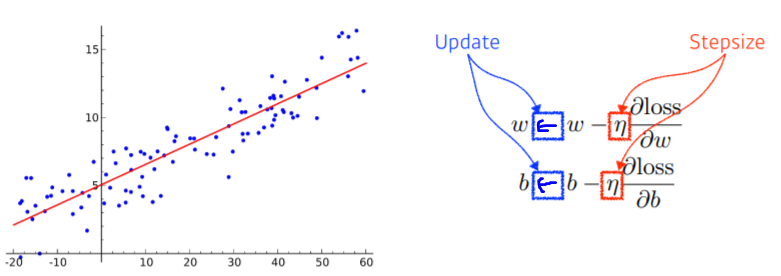
그림으로 나타내보면...

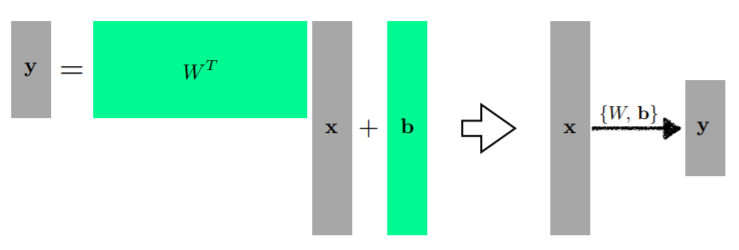
• N차원을 M차원 model로 바꾸기 위해서는 행렬을 사용한다.
  
  

행렬을 곱하는 것은 어떤 의미를 갖는가?

• 2개의 Vector Space간의 변환
  • 선형성을 가지는 변환을 행렬로 표현하는 것
  • 2가지 다른 차원(Vector Space)간의 선형 변환을 찾는 것
    
    

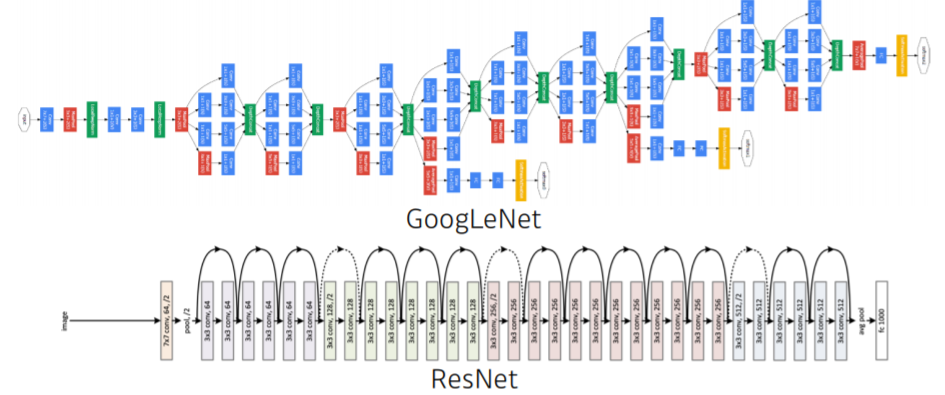
좀 더 깊게 쌓아보면...

• bias 생략된 그림
  

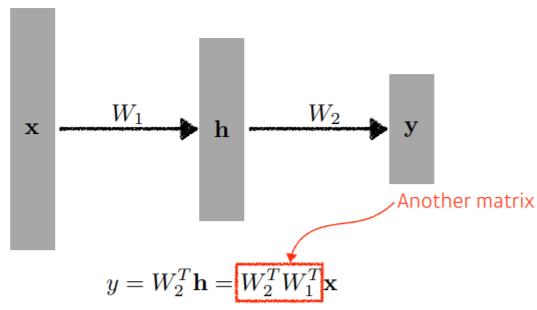
• $W_2^TW_1^T$ 가 행렬곱으로 되어있기 때문에 단층 Neural Network와 다를 바가 없다!

• 따라서 이를 Nonlinear 함수 (Activation funcion)에 넣어준다.
  

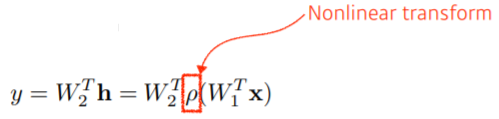
• 여러가지 Activation Function들
  

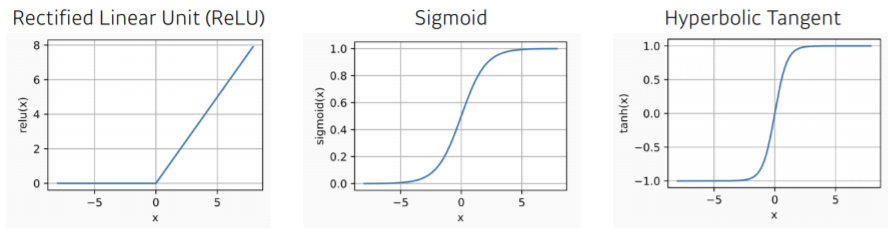
Neural Network의 표현력

• Hidden layer가 1개 있는 Neural Network으로 우리가 일반적으로 생각할 수 있는 대부분의 continuous한 function들을 모두 표현할 수 있다. 표현력이 크다
• 표현력이 크지만, 어떻게 찾는지는 모른다
• 이런게 어디엔가 있다 이지, 내가 학습시킨 Neural Network가 그러하다 라고 할 수는 없음.