Support Vector Machine (SVM)
- 분류를 하기 위한 경계선(결정선)을 찾는 것
- 두 클래스 간의 거리(마진)를 가장 넓게 분리 할 수 있는 경계선이 최적의 분류 선
- SVM 목표: support vector간의 가장 넓은 margin을 가지는 결정 경계를 찾기
- Support Vector: 경계를 찾는데 기준(지지하는)이 되는 데이터포인트. 결정경계에 가장 가까이 있는 1차원의 값vector(데이터포인트)를 말한다. 하나가 아닐 수도 있음
- margin: 두 support vector간의 너비
규제 파라미터 - Hard Margin, Soft Margin
- 마진을 결정하는데 가장 큰 문제는 이상치(outlier)
- 이상치를 얼마나 무시할 것인지에 따라 Hard Margin, Soft Margin으로 나눔
- Hard Margin
- 이상치를 무시하지 않고 서포트벡터를 찾음
- overfitting 발생 가능
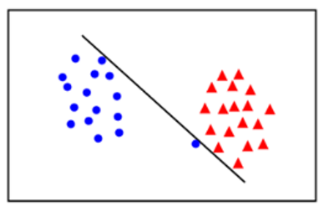
- Soft Margin
- 일부 이상치를 무시하고 서포트벡터를 찾음
- underfitting 발생 가능
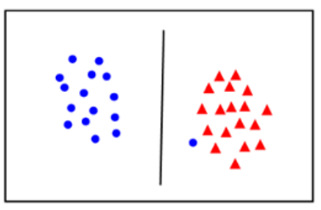
⇒ 하이퍼파라미터 C 값으로 조정
- 이상치를 무시하는 비율을 설정하는 하이퍼파라미터
- 기본값 = 1
- overfitting : C의 값을 줄인다.
- underfitting : C의 값을 늘린다
| 작은값 | 적당한값 | 큰값 |
|---|---|---|
| underfitting | generalization | overfitting |
| soft margin (약한규제) | hard margin (강한규제) |
⇒ Feature scaling ( SVM 전처리)
- 연속형 : Feature scaling
- 범주형 : One Hot Encoding
💡 선 그래프를 그릴 때, x축,y축 값의 차이가 클 경우 변화의 차이(흐름)를 제대로 확인하기 어려움
⇒ 한 번 크게 변한 뒤 변화량이 크지 않을 때 → 범위를 좁힘 : ylim(최소, 최대), xlim(최소, 최대)
⇒ 지수적으로 증가(간격이 점점 커진다) → log 사용 : C_list_log = np.log10(np.array(C_list))
Kernel SVM (비선형(Non Linear) SVM
💡 predict_proba() 메소드를 사용할 때 (양성의 확률을 볼 때)
→ SVC 객체 생성시 파라미터 probability=True 로 설정
## 예시
svc = SVC(C=1.0, gamma=0.001, random_state=0, probability=True)
svc.fit(X_train_scaled, y_train)
pos = svc.predict_proba(X_train_scaled)[:, 1]
average_precision_score(y_train, pos), roc_auc_score(y_train, pos)K-최근접 이웃 (K-Nearest Neighbors, KNN)
- 분류 : 추론할 feature들과 가까운 feature들로 구성된 data point K 개의 y중 다수의 class로 추론
- 회귀 : 추론할 feature들과 가까운 feature들로 구성된 data point K 개의 y값의 평균값으로 추론
- K가 작을수록 복잡한 모델
- Overfitting: K값을 더 크게 잡는다.
- Underfitting: K값을 더 작게 잡는다
- Feature간의 값의 단위가 다르면 작은 단위의 Feature에 영향을 많이 받게 되므로 전처리로 Feature Scaling작업이 필요
- 훈련셋이 너무 큰 경우 예측이 느려짐, 추론 시간이 많이 걸림, 성능용으로 편차가 큼 → base line을 잡기 위한 모델로 많이 사용(복잡한 알고리즘을 적용하기 전)
주요 하이퍼 파라미터
- 분류: sklearn.neighbors.KNeighborsClassifier
- 회귀: sklearn.neighbors.KNeighborsRegressor
- n_neighbors = K
- K가 작을 수록 모델이 복잡해짐
- 유클리디안 거리(Euclidean distance - 기본값 - L2 Norm)
- p=2
- 평면에서의 직선 거리 재는 방법
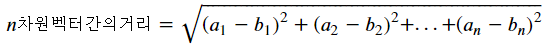
- 맨하탄 거리(Manhattan distance - L1 Norm)
- p=1
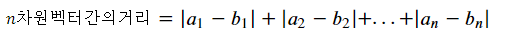
- p=1
