안녕하세요. 밍기뉴와제제입니다. 오랜만에 논문 리뷰를 합니다.
이번에 리뷰할 논문은 'NeRF: Representing Scenes as
Neural Radiance Fields for View Synthesis', 줄여서 NeRF입니다. 이름을 많이 들어봤는데 드디어 리뷰하네요.
그러면 지금부터 리뷰를 시작하겠습니다.
1. Introduction
객체를 찍은 여러장의 사진을 입력받아 새로운 view에서 바라본 객체의 모습을 알아내는 view synthesis라는 task가 있습니다. 이게 성능이 썩 좋게 나오지는 않고 있었는데 저자가 새로운 방식을 제안합니다.
새로운 방식
저자는 5차원 데이터 (x, y, z, θ, φ)를 입력받아 해당 시점에서 바라봤을 때 객체에서 추출되는 radiance와 density를 추출하는 함수를 고안했습니다.
- 이 때 radiance는 ‘(x, y, z)에서 (θ, φ) 방향으로 방출되는 광원’이고 density는 ‘(x, y, z)를 지나는 레이저(가상의 레이저. 시점을 벡터로 나타낸 것이라 보시면 됩니다)에 축절되는 광원을 제어하는 differential opacity같이 작동하는’ 것입니다. density에서 100%이해하려니 힘드네요.
저자는 어떻게 (x, y, z, θ, φ)를 입력으로 넣어 radiance와 density를 얻는 함수를 만들었을까요? 여기서 저자는 딥러닝 알고리즘을 사용했습니다. (x, y, z, θ, φ)를 입력받아 single volume density와 view-dependent RGB를 출력하는 MLP를 설계한 것이죠. 딥러닝 알고리즘이 메인 요소가 아니라 문제 해결을 위한 과정 중에 쓰이는 일반적인 요소 중 하나로 사용된 것입니다. 그리고 classical volume rendering techniques을 이용해 MLP로 얻은 RGB와 density 데이터들을 2D 이미지에 축적하여 새로운 관점에서 객체를 바라봤을 때 scene을 얻을 수 있죠. 저자는 자신이 말한 방식을 neural radiance field(NeRF)라고 이름 지었습니다. 게임의 너프가 떠오르는 이름입니다. 정감가네요.
저자는 자신이 제안한 NeRF를 수행하기 위한 과정, 그러니까 앞서 말씀드린 과정을 다음과 같이 3가계 단계로 정리하였습니다.
- 3D point의 sampled set 생성하기(바라볼 관점들을 지정합니다.)
- 생성한 sampled set과 sampled set에 해당하는 2D viewing direction을 MLP에 넣어 해당 위치에서 바라본 객체의 color와 density 얻기
- classical volume rendering techniques으로 휙득한 color와 density를 2D 이미지에 축적하기
- 저는 NeRF를 보며 사람의 뇌가 떠올랐습니다. 사람도 머릿속으로 해당 지점에서 객체의 특정 부분을 살펴본 뒤 아직 살펴보지 않은 지점을 상상할 수 있잖아요. 저자가 제안한 네트워크도 그렇게 작동하는듯한 느낌이 들었습니다.
해당 과정을 그림으로 나타내면 다음과 같습니다.
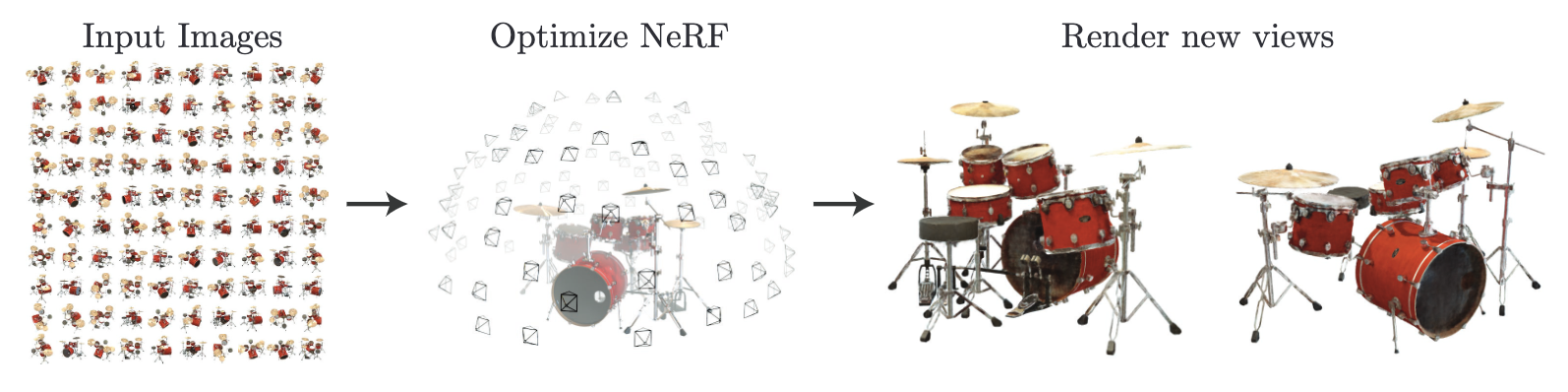
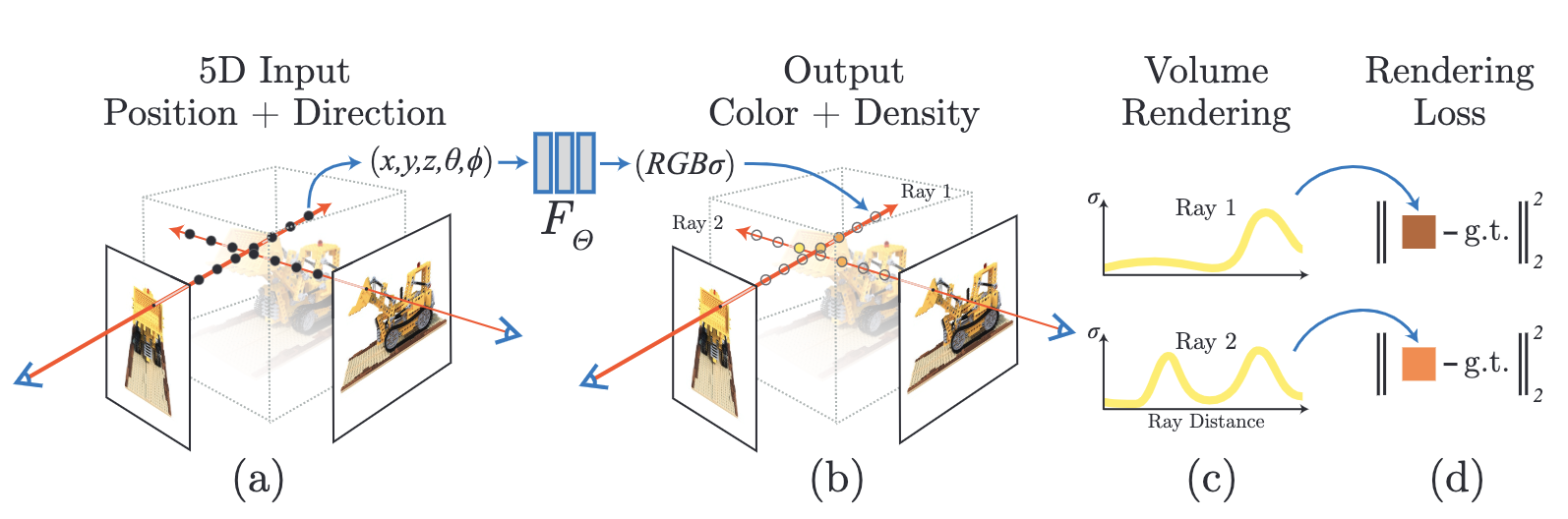
저자는 NeRF를 수행하는 과정이 미분이 가능하다고 말했습니다. 즉, 해당 지점에서 실제로 관측된 이미지(scene)와 MLP로 만들어진 ‘추측된' 이미지 사이의 에러를 계산해 경사하강법으로 MLP를 최적화 시킬 수 있다는 것이죠. 이렇게 여러 관점에서 관측된 이미지의 에러를 줄일 수 있으면 새로운 관점에서 관측될 이미지를 더 정확히 관측할 수 있을 겁니다.
부족한 점을 발견, 보완하다
저자는 복잡한 scene을 표현하기 위한 NeRF를 최적화하는 basic implementation이 좋지 못한 성능을 보이며 더 많은 sampled set이 필요하다는 사실을 알아냈습니다. 그래서 positional encoding을 이용해 (x, y, z, θ, φ) 데이터를 변환, NeRF에 쓰이는 MLP가 더 높은 주파수도 표현할 수 있게 만들었습니다.
여기서 더 높은 주파수를 표현할 수 있다는 말은 경계선을 표현하는 능력이 더 증가한다는 뜻입니다. 이미지의 저주파 대역은 배경, 고주파 대역은 테두리 등 RGB 데이터의 변동이 심해지는 지역을 나타냅니다.
그리고 hierarchical sampling procedure을 도입해 요구되는 쿼리의 숫자를 감소, 고주파의 scene을 표현할 때 필요한 sampled set를 적절한 개수만큼 선별하게 만들었습니다.
NeRF로 얻는 이득
NeRF는 현실세계에 존재하는 복잡한 모양의 객체들을 표현할 수 있고 우리 눈에 사영된 이미지들을 사용하여 gradient-based optimization을 수행할 수 있습니다. 논문에 의하면 ‘NeRF는 volumetric representation의 이점을 상속 받았기 때문에' 가지는 장점이라고 하네요.
그리고 복잡한 객체의 scene을 고해상도로 모델링할 때 필요한 cost가 discretized voxel grids로 모델링 할 때 필요한 cost보다 훨씬 적다는 이점도 가지고 있습니다. 적은 용량만 있어도 3D모델의 scene을 생성할 수 있는 것이죠. 3D 파일들이 많은 용량을 가지고 있는 것을 생각했을 때 상당히 큰 장점이 아닌가 생각됩니다.
정리
저자는 Introduction을 끝내기 전에 NeRF의 contribution을 다음과 같이 정리했습니다.
- MLP 네트워크로 continuous scenes with complex geometry and materials을 표현하는 방식을 제안
- classical volume rendering techniques 기반의 미분 가능한 렌더링 방식(MLP의 순방향 연산)을 제안. MLP는 렌더링 과정에서 얻은 값과 실제 데이터 사이의 오차를 미분해(미분 가능하므로) parameter 학습을 수행합니다.
- 5차원 입력 데이터를 더 고차원 데이터로 mapping하는 positional encoding을 제안. positional encoding 덕분에 NeRF가 고주파의 scene을 성공적으로 표현할 수 있게 만들었습니다.
그리고 저자는 NeRF가 논문을 쓸 당시에 가장 성능이 좋았던 모든 view synthesis 방식들보다 더 좋은 성능을 보여줬다고 합니다. 이에 대한 자세한 내용은 아래 Results에서 설명드리도록 하겠습니다.
2. Neural Radiance Field Scene Representation
앞서 말씀드렸듯, 저자는 입력데이터로 (x, y, z, θ, φ), 다시 말해 3D 좌표 X = (x, y, z)와 X에서 바라보는 방향 (θ, φ)을 받아 color (r, g, b)와 volume density σ를 출력하는 함수를 만들었습니다. NeRF에 쓰이는 MLP를 말하는 것이죠. 이 때 특정 위치 (x, y, z)에서 객체를 바라보는 방향 (θ, φ)을 직교 좌표계 (x, y, z)로 구성된 unit vector d로 표현했다고 합니다.
즉, 저자는 5차원 데이터 (x, y, z, θ, φ)로 scene을 나타내는 방식을 (X, d) → (c, σ)로 매핑하는 MLP로 구현하였으며 이 MLP의 parameter Θ를 학습시켜 더욱 현실에 가까운 scene을 만들도록 만든 것이죠. 앞서 말했던 것을 조금 더 구체적으로 설명한 것이라 볼 수 있겠습니다.
어떤 시각에서 봐도 성능 변화가 없게끔 만들다
보통 네트워크를 설계하고 학습시키다 보면 특정 케이스에서는 성능이 잘나오지만 다른 특정 케이스에서는 성능이 안나올 때가 있습니다. 특정 상황에 많이 편향되게 학습이 진행된 것이죠. NeRF가 수행하는 view synthesis에서는 ‘특정 시각에서 관측되는 scene만 잘 예측하는 것'으로 볼 수 있겠습니다.
그래서 저자는 이러한 문제를 다음과 같은 방식으로 해결하고자 하였습니다.
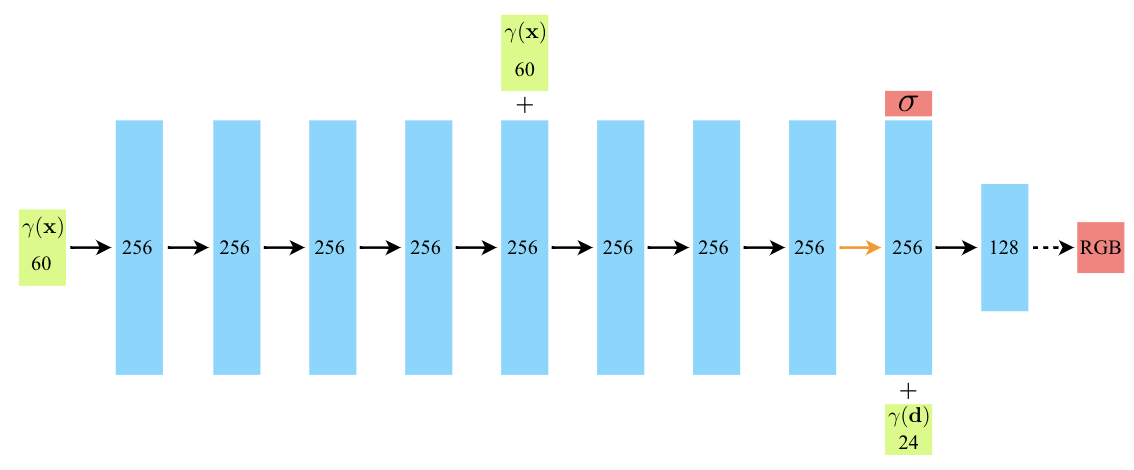
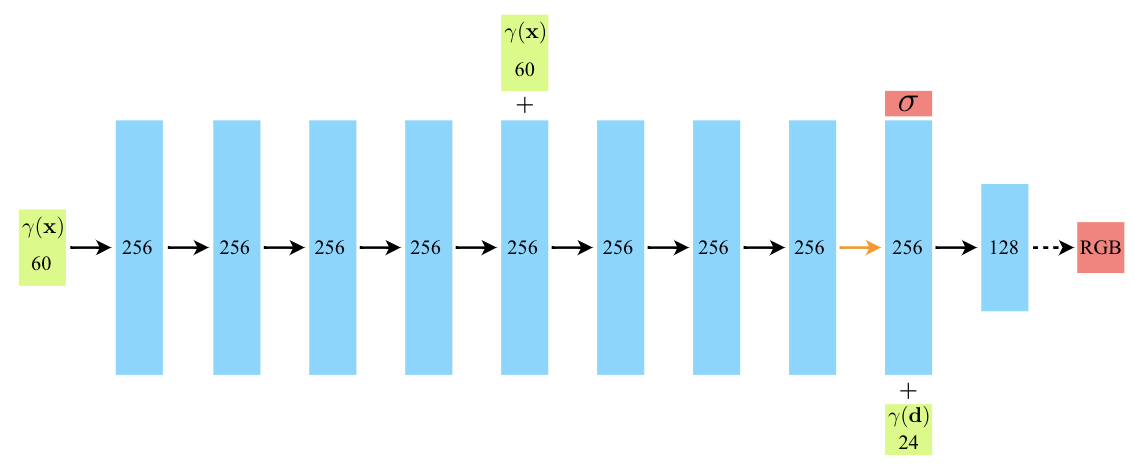
- X만 가지고 volume density σ을 예측하게 만들기 : 8개의 fully-connected layer(256개의 뉴런을 가지고 있음)로 구성된 MLP가 X를 입력받아 σ와 256차원의 feature vector를 출력
- X와 d를 모두 사용해 c를 예측하게 만들기 : MLP로 예측한 256차원의 feature vector를 (θ, φ)와 합치고(concatenate) 128개의 뉴런을 가진 fully-connected layer에 넣어 view-dependent RGB를 휙득
여기서 나온 MLP, fully-connected layer는 모두 ReLU를 활성화 함수로 사용합니다.
아래 그림을 통해 저자가 제안한 방식의 예시와 그 효과를 알 수 있습니다. (위 : 예시, 아래 : 효과)
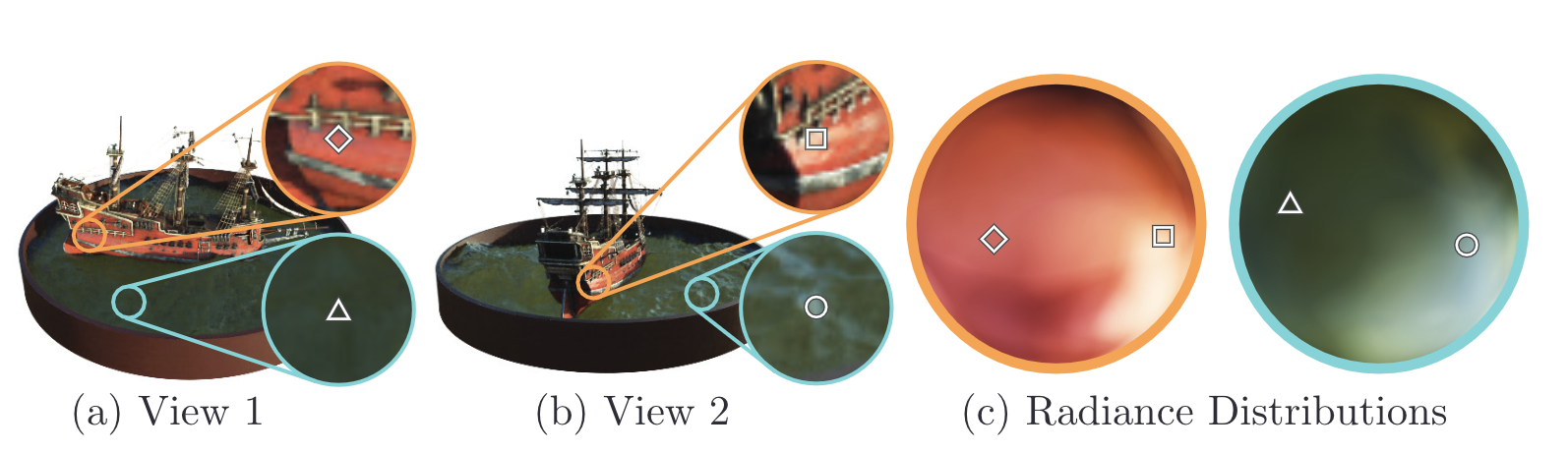

3. Volume Rendering with Radiance Fields
우리는 지금까지 MLP로 해당 위치에서 바라본 객체의 volume density와 RGB를 휙득하는 부분까지 살펴봤습니다. 앞서 NeRF는 ‘classical volume rendering techniques’을 이용해 렌더링을 수행한다고 말씀드렸죠? 이번 장에서 그에 대해 자세히 나와있습니다.
렌더링될 색상 구하기
우선 렌더링될 색상을 구하는 식을 살펴봅시다. 논문에서 말하길 MLP로 구한 volume density는 ‘X에 존재하는 아주 작은 입자에서 사라지는 레이저가 미분이 가능할 확률로 해석할 수 있다'고 합니다. 우리가 바라볼 위치에서 나아갈 가상의 레이저가 미분이 될 확률을 volume density로 알 수 있다니 신기합니다.
여튼, 이러한 성질을 가지고 있는 가상의 레이저, 다시 말해 camera ray r(t) = o + td와 ray의 구간을 결정하는[t_n, t_f]를 이용해 우리는 camera ray와 충돌하는 객체의 일부분을 렌더링 할 때 사용할 색상을 다음의 식으로 결정할 수 있습니다.
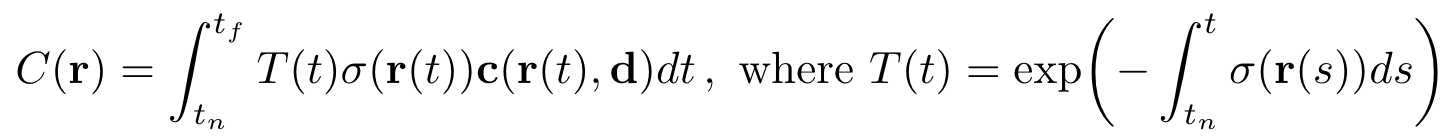
식에 대해 자세히 설명드리겠습니다. 여기서 T(t)는 ray가 t_n부터 t까지 객체를 통과하며 축적된 투과율을 말합니다. 우리가 발사하는 가상의 레이저가 객체의 여러 점들을 통과할 것입니다. 그 때 만나는 여러 점에서 구한 투과율을 축적하는 것이죠. 이를 달리 말하면 ‘camera ray가 t_n부터 t 구간에 있을 때 객체와 접촉하지 않을 확률'로 해석할 수 있겠습니다. 적절한 표현이라 생각됩니다. 우리가 바라본 시점에 객체가 없으면 멀리 있는 것도 보이지만 앞에 불투명한 객체가 있으면 가까이 있는 객체만 보이잖아요.
저자는 ‘NeRF를 이용해 scene을 생성하려면 desired virtual camera가 발사하는 가상의 광선이 접촉하는 픽셀들을 가지고 C(r)을 측정한 값이 필요하다'고 말했습니다.
stratified sampling approach(층화표집)
그러면 C(r)을 실제로 계산하려면 어떻게 해야될까요? 방식은 여러가지가 있죠. 우선 Deterministic quadrature, 다시 말해 적분할 구간을 사각형으로 근사화 후 다 합치는 적분 기법이 있습니다. 이는 voxel grid를 렌더링 할 때 많이 쓰는 기법이라고 하네요. 그런데 NeRF에서 이 방식을 사용하면 MLP가 fixed discrete set of location의 값을 가지고 discrete한 적분을 수행하기 때문에 성능이 제한되어 버린다고 합니다. 적분할 때 쓰는 값의 개수가 항상 같기 때문에 가상의 레이저가 접촉하는 좌표가 객체가 아닌 공기일 수도 있다는 것이죠. 즉, ‘가상의 camera ray가 접촉하는 모든 점에서 sampling한 t_i들을 가지고 적분을 수행하기 때문에 불필요한 pixel도 적분 범위에 들어가 성능이 제한되어 버리는 것’입니다.
그래서 저자는 다른 방법을 썼으며 그 방식의 이름이 바로 ‘stratified sampling approach’입니다. stratified sampling approach는 C(r)의 적분 구간으로 사용했던 [t_n, t_f]를 일정한 N개의 구간으로 나누고 각 구간에서 임의로 하나씩 뽑아 discrete한 적분의 구간으로 사용합니다.
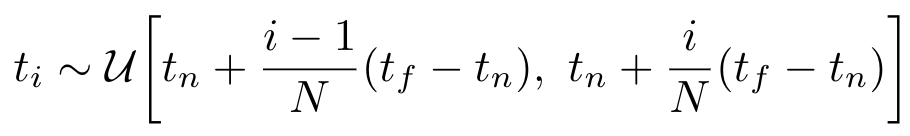
(stratified sampling approach로 선별하는 t_i를 뽑는 방식)
이렇게 적분에 쓸 값을 선별하면 ‘continuous position을 처리하는 MLP에서 얻은 값에서 선별하기 때문'에 유효한 값들에서 sampling을 수행할 수 있습니다. 그렇게 sampling한 t_i들을 가지고 적분을 수행하면 더 높은 성능이 나오겠죠. 참고로 이 때 수행하는 적분 역시 quadrature rule을 따르는 discrete한 적분이며 식은 다음과 같습니다.
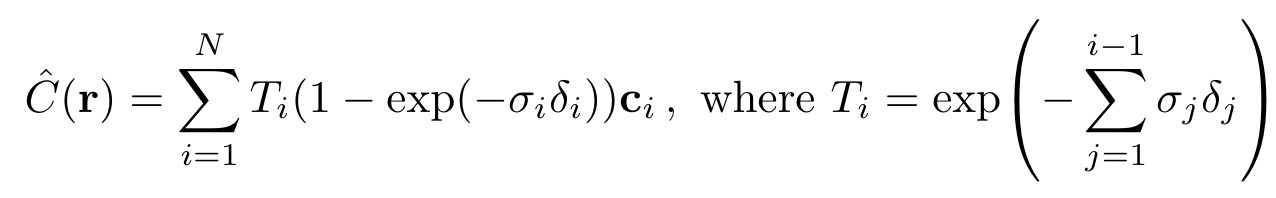
(δi = t(i + 1) − t_i는 인접한 sample 사이의 거리를 나타냅니다.)
이 식으로 구한 C(r)은 trivially differentiable하며 alpha를 α_i= 1−exp(−σ_i x δ_i)와 합치기 때문에 값이 감소한다고 하는데 음...어떤 의미인지는 잘모르겠습니다.
4. Optimizing a Neural Radiance Field
이번 장에는 앞서 설명드린 Positional Encoding과 hierarchical sampling procedure에 대해 자세히 설명되어 있습니다. 이 둘은 NeRF가 고주파의 복잡한 scene을 표현할 수 있게 도와준 요소들이죠. 이 둘의 역할을 다시 한 번 간단히 정리하자면 다음과 같습니다.
- Positional encoding : MLP가 고주파 데이터를 처리할 수 있게 도와줌. 입력 데이터에 적용
- Hierarchical sampling procedure : NeRF가 고주파 scene을 효율적으로 sample할 수 있게 만들어줌.
그러면 지금부터 하나씩 자세히 설명해보도록 하겠습니다.
4.1 Positional encoding
저자는 네트워크 F_Θ가 (x, y, z, θ, φ) 좌표를 바로 처리하였을 때 고주파 영역의 렌더링 성능이 크게 떨어진다는 것을 발견했습니다. 그리고 저자 외에도 다른 연구자가 이러한 현상을 발견했는데요, 그는 ‘네트워크가 저주파를 처리하는 함수로 학습되기 때문'에 이러한 현상이 일어난다고 말했습니다.
그리고 ‘고주파 함수로 입력 데이터를 더 고차원 데이터로 매핑하고 네트워크에 입력값으로 넣으면’ 고주파 영역의 처리 성능이 향상된 방향으로 학습되는 것’도 발견하였습니다.
저자는 이 점을 NeRF에 적용하였습니다. 그리고 네트워크 FΘ = F’Θ ◦ γ로 재구성 하였을 때 성능이 매우 크게 향상된다는 점을 발견했습니다. 여기서 F’_Θ는 simply a regular MLP이며 γ는 R차원에서 R^(2L)차원으로 매핑하는 함수이며 식을 자세히 적으면 다음과 같습니다.
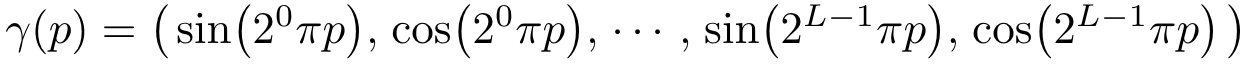
γ(·)는 입력 데이터 X = (x, y, z)의 각 원소 x, y, z와 X를 통과하는 camera ray의 unit vector d의 원소 x, y, z 모두 적용하여 해당 값들을 [-1, 1] 범위에서 normalize합니다.
Positional encoding은 transformer를 읽어보신 분들에게 매우 익숙한 단어일 것입니다. 그러나 여기서 쓰는 것과는 조금 다르며 둘을 비교해보면 다음과 같습니다.
- transformer의 positional encoding : 입력값의 순서에 대한 개념이 없는 네트워크에 입력값으로 들어갈 토큰에 순서라는 개념을 부여하기 위해 사용됨
- NeRF의 positional encoding : 연속적인 입력 데이터의 좌표들을 좀더 고차원 데이터로 매핑해 MLP가 좀더 쉽게 고차원 성분, 즉 scene에 있는 테두리들을 좀더 쉽게 근사할 수 있게 만들기 위해 사용됨
4.2 Hierarchical volume sampling
저자는 원래 camera ray에서 N개의 포인트를 임의로 뽑은 후 렌더링에 사용하려고 했는데 이렇게 하니 비효율적이라는 것을 깨달았습니다. 왜냐하면 camera ray가 통과하는 공간은 객체뿐만 아니라 아무것도 없는 공간도 포함되어 있기 때문이었죠. 별 도움이 안되는 것들도 렌더링에 사용하니 좋은 결과가 나오기 힘들었던 것입니다.
그래서 생각해낸게 마지막 렌더링에서 예측되는 효과에 비례해 포인트를 sampling하는 방식인 Hierarchical volume sampling 이었습니다. 이렇게 하면 효율적으로 렌더링에 사용할 좌표를 뽑을 수 있다고 하네요.
두개의 네트워크를 사용
저자는 NeRF에 사용할 네트워크를 하나가 아닌 두개로 설정했으며 각각 “coarse” 네트워크, “fine” 네트워크라고 이름 지었습니다. 우선 “coarse” 네트워크를 어떻게 사용하는지 알아보도록 합시다.
- camera ray에서 stratified sampling을 사용해 N_c개의 구간에서 값을 하나씩 뽑습니다. 그리고 해당 값을 가지고 C(r)을 계산합니다. (이 때 “coarse” 네트워크를 사용합니다.)
- 구한 값에서 얻은 정보를 통해 volume density가 상대적으로 높은 좌표를 위주로 값을 뽑습니다.
그리고 이를 수행하기 위해서 alpha composited color를 구하는 식 C_c(r)을 다음과 같이 c_i의 weighted sum으로 재정의 해야합니다.
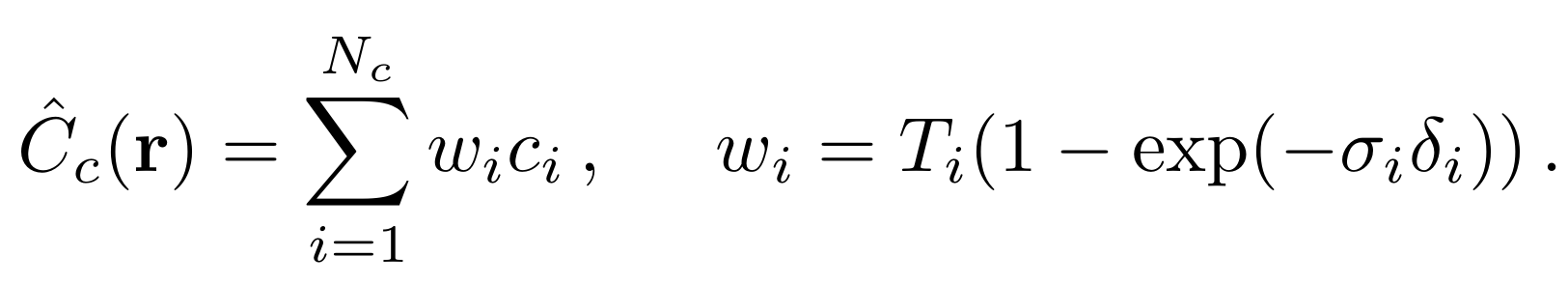
식 5에서 사용되는 weight w_i를 normalizing할 경우, w_i는 부분적으로 일정한 PDF가 된다고 합니다.
다음으로 “fine” 네트워크를 사용하는 경우를 알아봅시다.
- camera ray에서 inverse transform sampling을 사용해 N_f개의 위치에서 값을 하나씩 뽑습니다.
- “fine” 네트워크를 이용해 C_f(r)을 계산하는데 이 때 “coarse”네트워크에 넣었던 N_c개의 값도 같이 사용합니다. 즉, “fine” 네트워크에 N_c + N_f개의 데이터를 입력값으로 넣는 것이죠.
이렇게 하면 우리가 visible content가 포함될 것으로 예측되는, 그러니까 실제 객체가 존재할 영역에 있을 좌표를 더 많이 사용하게 된다고 합니다. 즉, 허공이 아닌 실제 객체를 렌더링에 사용하는 비중이 더 높아진다는 것이죠. 이는 곧 성능 상승으로 이어집니다. 논문에 의하면 ‘전체 적분 구간의 nonuniform discretization 으로 뽑힌 값들을 사용한다'고 나와있는데 음...제대로 이해하지 못했습니다. 여튼, 이런식으로 값을 뽑아서 렌더링에 사용하면 성능이 더 좋아진다고 이해하시면 되겠습니다.
4.3 Implementation details
여기서는 저자가 NeRF를 구현하기 위해 사용한 세팅을 설명하는 장입니다. 보통 다른 논문에서는 Experiment에서 setup을 설명할 때 나오는데 여기서는 Experiment 이전에 나오네요. 정확히는 학습 과정에 대해 자세히 설명해놨습니다. 하나씩 설명해보도록 하겠습니다.
- scene이 저장된 이미지, 해당 이미지를 촬영한 카메라, 카메라의 intrinsic parameters(카메라에 있는 이미지 센서의 크기 등 카메라의 고유 성질), scene bounds로 구성된 데이터셋을 휙득합니다.
- 학습 과정에서 매 epoch마다 camera ray를 만나는 데이터셋의 pixel들을 일부 선별, hierarchical sampling을 수행해 N_c개의 값을 넣어 “coarse” 네트워크에 넣어 값을 얻고 N_c + N_f개의 값을 “fine” 네트워크에 넣어줍니다.
- volume rendering procedure을 수행해 camera ray로 바라본 지점의 색상을 렌더링합니다.
- “coarse” 네트워크를 사용해 렌더링한 값과 “fine” 네트워크를 사용해 렌더링한 값과 실제로 렌더링된 값을 가지고 loss를 구합니다. 이 때 사용하는 loss는 total squared loss입니다.
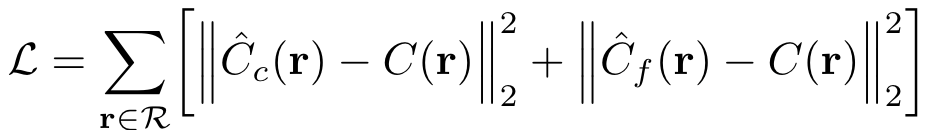
(total squared loss)
여기서 R은 각 batch에 있는 camera ray의 집합을 말하며, C(r), C_c(r), C_f(r)은 각각 ground truth, “coarse”로 얻은 값, “fine” 네트워크로 얻은 값을 나타냅니다.
실제 학습되는 네트워크는 하나
앞서 우리는 “fine” 네트워크와 “coarse” 네트워크를 사용해 loss를 구했습니다. 그러나 “coarse” 네트워크만 학습을 수행합니다. 저자는 “coarse” 네트워크가 “fine” 네트워크에 있는 샘플들을 할당하는데 이용하기 위해서라고 하네요. 생각해보면 두개의 네트워크를 같이 쓴다고 했을 때 하나의 네트워크만 학습시켜도 우리가 원하는 값을 출력하게끔 학습시킬 수 있으니까 (학습을 시키지 않은 네트워크는 변하지 않는 상수 함수(?)로 판단할 수 있겠죠) 하나만 학습시키는게 학습 시간을 아낄 수 있겠구나 생각됩니다.
그리고 실험에 사용된 GPU, hyper parameter 등이 있는데 이는 생략하도록 하겠습니다.
5. Results
이제 실험결과를 설명해드리도록 하겠습니다.
5.1 Datasets
저자가 사용한 데이터셋을 각각 설명드리면 다음과 같습니다.
- DeepVoxels(Diffuse Synthetic 360) : 구조가 단순하며 람베르트 반사 성질(어느 시점에서 빛을 발사해도 모든 방향으로 균일하게 반사되는 이상적인 성질)을 지닌 표면으로 구성된 4개의 객체로 만들었습니다. 각 객체를 촬영한 scene의 해상도는 512 x 512이며 반구형 궤적을 그리며 촬영하였습니다.
- our own dataset(Realistic Synthetic 360) : 저자가 추가적으로 제작하였습니다. 8개 객체를 가지고 제작하였으며 모두 논-램베르트 반사 성질(현실적인 반사 성질)을 지녔습니다. 6개 궤적은 반구형 궤적을 그리며 촬영했으나 2개는 구형 궤적을 그리며 촬영했습니다. 촬영한 사진의 해상도는 800 x 800입니다.
5.2 Comparisons
논문을 썼던 당시 가장 좋은 성능을 보여주던 것들과 비교한 결과를 설명합니다.
Quantitatively result
우선 수치적으로 비교해보겠습니다. 저자는 실험 결과를 표로 정리했는데요, 다음과 같았습니다.

여기서 PSNR은 최대 신호 대 잡음비(Peak Signal-to-noise ratio)를 나타낸 값으로 이미지의 화질 손실 정보를 평가할 때 사용되는 수치입니다. 높을 수록 좋습니다. 그리고 SSIM은 구조적 유사성 측정값(structural similarity index measure)을 나타내는 수치입니다. 이미지의 품질을 측정할 때 많이 사용되는 수치이며 역시 높으면 좋은 값입니다.
마지막으로 LPIPS는 Learned Perceptual Image Patch Similarity의 줄임말입니다. 제가 링크로 연결해놓은 리포지터리의 논문에서 제시한 단위이며 ‘이미지 패치 사이의 거리'를 측정합니다. 이게 짧으면 두 이미지는 유사한거고 길면 두 이미지가 다른 것이죠.
표에 나와있는 데이터셋 중 Read Forward-Facing에 관한 설명은 나와있지 않아서 적지 못했습니다.
Qualitatively result
저자는 결과물도 올려 시각적으로 비교할 수 있게 만들었습니다. 여기서 저자가 직접 만든 데이터셋(our own dataset)을 사용했습니다.


Result에서 비교에 사용한 네트워크에 관한 설명도 적혀있는데 NeRF에 관한 설명이 아니기 때문에 설명하지 않고 넘어가도록 하겠습니다.
5.3 Discussion
여기서는 기존에 사용했던 방식들이 가지는 제약을 얘기하며 NeRF의 장점을 또다시 강조합니다. 여기서 살펴볼 특이점은 NeRF가 정말 적은 용량만 요구한다는 점입니다. NeRF에서 사용하는 MLP의 parameter는 고작 5MB의 용량만 차지하며 15GB를 요구하는 LLFF와 비교했을 때 적말 적은 용량입니다. 저자가 제작한 데이터셋에 있는 이미지보다 적은 용량이라고 하네요.
5.4 Ablation studies
여기서는 제목 그대로 NeRF를 구성하는 중요 요소들을 제거하며 관찰되는 성능 하락을 통해 NeRF를 위해 저자가 제안한 것들이 얼마나 효과적이었는지 보여줍니다. 우선 결과표를 확인해봅시다.

(여기서 PE는 ‘Positional Encoding’, VD는 ‘View Dependence’, H는 ‘Hierarchical Sampling’입니다.)
표에서 눈여겨볼 부분은 5, 6번째 열(row)입니다. 입력값으로 넣은 이미지 개수에 따라 성능이 상승하는 것을 관찰할 수 있는데 가장 적은 이미지 개수인 25장을 사용해도 기존 네트워크 중 가장 좋은 성능을 보여줬던 NV, SRN, LLFF보다 더좋은 성능을 보여준다는 겁니다. 그리고 7, 8번째 열은 NeRF가 처리할 최대 주파수에 따른 성능 변화를 나타낸 데이터입니다.(입력받은 위치 벡터 X를 positional encoding할 때 최대 주파수를 L로 설정합니다.) 최대 주파수가 늘어나는만큼 생성할 scene의 디테일을 더 강화되어 성능 향상이 될 것이라 기대하였으나 실험 결과, 최대 주파수를 10보다 늘리자 오히려 성능이 하락하는 것을 발견할 수 있었습니다. 최대 주파수를 5에서 10으로 늘릴 때는 저의 추측과 같이 L이 증가가 곧 성능의 증가로 이어졌죠.
저자는 이러한 결과를 보며 ‘2^L가 maximum frequency present를 능가할 경우 L을 늘렸을 때 얻는 이득이 제한되는 것이라 믿고 있다'고 말했습니다. 저자가 사용한 데이터셋은 ‘maximum frequency present’를 대략 1024일 것이라 보고 있습니다. 그러면 L=10으로 했을 때 최대 성능이 나오는게 말이 되는 것이죠.
6. Conclusion
저자는 continuous function과 같이 MLP를 사용해 객체의 scene을 표현하는 방식을 사용해 기존의 view synthesis가 가지던 성능의 한계를 해결하였습니다. 저자는 CNN을 사용해 voxel로 scene을 표현하는 기존의 주요 방식보다 자신이 제안한 NeRF가 더 좋은 성능을 지녔다는걸 보여줬죠. 그리고 NeRF가 더 효율적으로 학습하고 렌더링할 수 있게 발전할 수 있는 여지가 있다고 말했으며 ‘딥러닝 네트워크로 얻은 값'을 효과적으로 표현하는 방식에 NeRF가 이용되면 더 좋은 성능을 얻을 수 있다고 말하며 논문을 끝냅니다. 여기서 제가 제대로 이해했는지 모르겠네요. 음...
후기
오랜만에 하는 논문 리뷰입니다. 어우...힘드네요. 그래도 완성하니까 뿌듯합니다. 앞서 말씀드렸듯 NeRF를 듣기는 많이 들었으나 자세히 읽어본건 이번이 처음인데 읽기를 잘했다는 생각이 듭니다.
이번학기 많은 논문을 리뷰하려고 했는데 생각보다 할 일이 많아 많이는 못할듯 합니다. 흑흑.
그래도 일주일에 한 번은 리뷰할 수 있도록 노력해보겠습니다.
다음 글에서 뵙겠습니다.
9개의 댓글
안녕하세요~ 좋은 정리와 내용 감사드립니다.
저는 NeRF에 대해 공부하며 찾아보던 중 궁금한 점이 생겨 댓글을 남겨둡니다
5D 데이터 5가지에서 ,xyz의 3차원 데이터가 어떻게 존재하는지가 궁금합니다.
이미지를 넣으면 2D이미지일텐데 xyz축 데이터를 어떻게 얻는지가 조금 헷갈려서요!
그래서 제가 이해하면서 추론?해본게 2가지인데,
첫 번째는 5d input 데이터에서 xyz는 n장의 이미지를 넣고 이를 통해 optimize한 3D의 모델의 위치 정보를 뜻한다
두 번째는 카메라 개념을 넣어보면 바라보는 카메라의 위치 xyz와 카메라가 바라보는 방향에 대한 데이터가 나머지 2가지이다.
로 생각해봤습니다. 제 생각에는 후자일 것이라고 생각하지만 정확히 이해하고싶어서 여쭈어봅니다!




잘 보았습니다. 감사합니다.