[논문리뷰] 'MLP-Mixer: An all-MLP Architecture for Vision' 리뷰 + 구현(PyTorch)

안녕하세요. 밍기뉴와제제입니다.

이번에 리뷰할 논문은 MLP-Mixer: An all-MLP Architecture for Vision입니다. MLP만 가지고 image classification을 수행한다는 것 때문에 화제가 되었던 논문이기도 합니다.

물론 Batch Normalization같은 것들도 들어있습니다.

MLP Mixer는 구조도 꽤 간단하고 필요한 parameter의 수가 적기 때문에 진입장벽(?)이 낮습니다. 그래서 PyTorch로 구현을 한 뒤 CIFAR-10 데이터셋으로 학습시켜봤습니다.

그리고 평범한 cnn과 residual block으로 제작한 cnn도 학습시킨 뒤 MLP-Mixer와 성능 비교를 해봤습니다. 자세한 설명은 나중에 해드리도록 하겠습니다.

그러면 논문 리뷰와 구현 코드 리뷰를 시작하겠습니다.

1. Introduction

2012년, AlexNet이 등장한 뒤로 Computer vision의 task들을 해결하기 위한 딥러닝 기반 네트워크의 대부분은 CNN(Convolutional Neural Network)이었습니다. 그러다 2020년에 ViT가 등장하며 attention mechanism을 가지고 Image classification을 하는 것으로 대세가 바뀌었죠.

그러나, 이러한 네트워크들은 parameter의 수가 많기 때문에 많은 데이터셋을 요구했고 이는 곧 많은 GPU 메모리와 저장장치의 용량을 요구했습니다. 성능이 확실한 대신 요구하는게 많았죠. 그리고 논문에 의하면, 여전히 large-scale image recognition에서는 2016년에 제안된 ResNet이 여전히 SOTA라고 합니다.

MLP'만' 사용해보자

그래서, 저자들은 딥러닝 기반의 네트워크의 가장 기본적인 형태라고 할 수 있는 MLP'만'가지고 image classification을 해보는 방식을 제안했습니다.

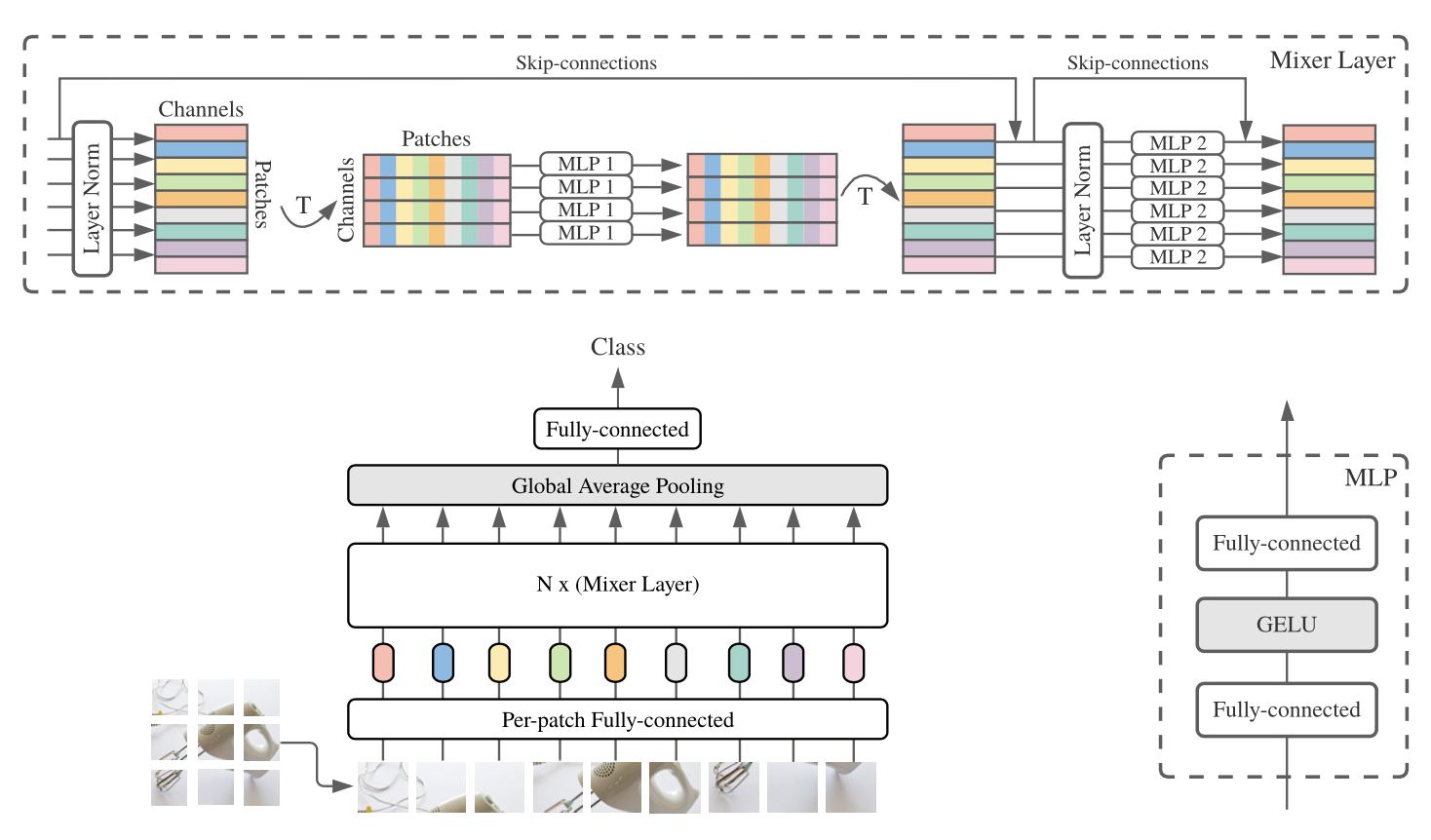
저자가 제안한 방식을 그림으로 나타내면 다음과 같습니다.

그림내용을 요약하면 '이미지를 N등분 해서 각각 처리 후 하나로 모아 classification을 수행한다'라고 할 수 있겠습니다.

그런데 여기 그림을 자세히 보시면 N등분한 이미지를 [per-patch fully connected]에 넣고 N층으로 구성된 Mixer Layer에 넣는 것을 확인할 수 있습니다. 이 때 Mixer -Layer가 바로 저자가 제안한 방식의 핵심요소입니다.

이 Mixer는 당연히 MLP로 구현된 Layer입니다. 그래서 저자는 제안한 네트워크의 이름을 'MLP-Mixer'로 정한게 아닌가 싶습니다.

'MLP'만 사용하고 음...

그래서 저는 MLP-mixer를 보며 'MLP를 사용한다는 것 말고는 CNN이랑 큰 차이가 없구나'라는 생각이 들었습니다. 물론 세부적인 연산 구조는 차이가 있긴한데 '각 지역 단위로 연산을 수행해 값을 추출 후 특정 task에 사용한다'는 것은 같습니다.

장점은 확실하다

그래도 장점은 많이 가지고 있습니다.

1. 모든 연산과정에서 '데이터'의 압축이 없다 : 제가 개인적으로 생각하는 장점입니다. MLP-Mixer는 맨 처음에 각 이미지를 patch별로 나눈 뒤 token으로 변환하고 연산을 수행합니다. 이 때 발생하는 정보의 손실을 제외한 나머지 부분에서는 데이터의 크기가 변하는 일이 없습니다. 즉, 레이어를 아무리 많이 쌓아도 연산으로 사용하는 텐서가 작아져 정보의 손실이 발생하는 일이 없는 것이죠.
2. 메모리 점유율이 낮다 : 같은 데이터셋으로 학습시켜 같은 task를 수행하는 모델을 만들 때 MLP-Mixer의 parameter 개수가 압도적으로 적습니다.

새로운 방식을 제안했다는 것

제가 'CNN과 큰 차이를 느낄 수 없는 방식'이라고 말하며 MLP-Mixer에 대한 아쉬움을 말하긴 했지만 그래도 MLP'만'가지고 image classification을 처리했으며 CNN과 attention mechanism이 주류인 분야에서 MLP로 주류 네트워크들과 비슷한 성능을 보여줬다는 것은 정말 대단한 성과라는 생각이 듭니다.

그래서 저는 MLP-Mixer가 마음에 듭니다. 그리고 제가 앞서 말씀드렸듯 구조가 꽤 간단하다고 말씀드렸습니다. 즉, 구현이 쉽다는 것이죠. 그래서 제가 구현할 수 있었던 겁니다.

그럼 이제 MLP-Mixer의 구조를 조금 더 자세히 살펴보도록 하겠습니다.

2. Mixer Architecture + 구현코드

지금부터 MLP-Mixer의 구조와 구현 코드를 살펴보도록 하겠습니다.

조금 더 자세히 살펴보자

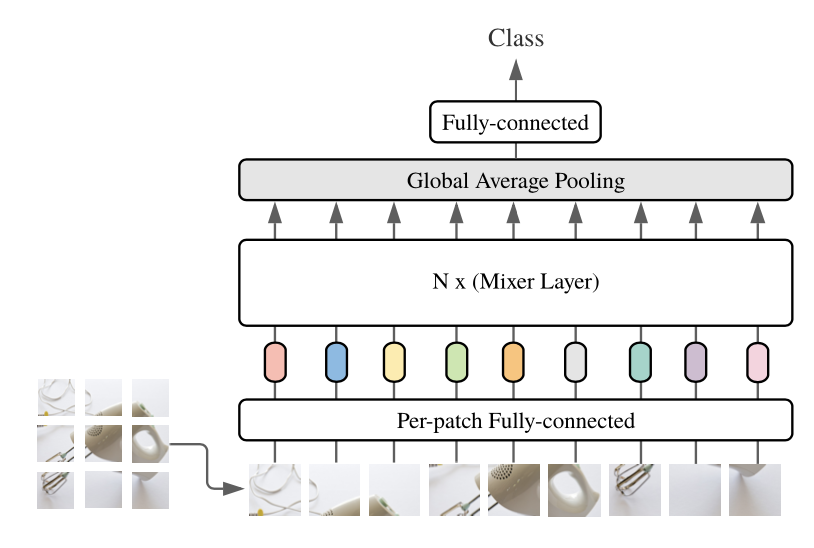
방금 제가 MLP-Mixer의 대략적인 구조를 보여드렸습니다.

이것 말이죠. 이 그림은 정말 대략적으로 나타낸 것이라 할 수 있습니다. 자세한 설명이 없으면 이해가 힘듭니다.

그러니 입력부터 출력까지 수행해야하는 과정들을 구현코드와 함께 자세히 설명해드리도록 하겠습니다.

2.1 입력받은 이미지를 S개의 Image Patch로 만들자

우선 입력받은 (3, H, W)크기의 input image를 (3, P, P)크기의 image patch로 나눠줍니다. 그러면 우리는 (H x W) / (P x P) = S개의 image patch를 얻을 수 있죠.

이를 코드로 나타내면 다음과 같습니다.

x = torch.reshape(x, (-1, self.S, input_channel * patch_size * patch_size))

보통 이미지 처리 네트워크의 학습을 수행할 때 입력 데이터의 형태가 (minibatch_size, 3, H, W) 입니다. 그래서 reshape를 할 때 변환되는 크기를 (-1,...)로 하였습니다. 그리고 patch의 모습에 맞게 (-1, 3, P, P)로 만들려고 했으나 바로 아래 2.2 연산을 수행할 때 (-1, 3 x P x P)로 만들어야 했기에 2.1 연산에서 (-1, 3 x P x P)로 reshape를 하였습니다.

2.2 Image Patch를 크기가 C인 token으로 만들자

다음으로 각 image patch들을 token으로 만들어줍니다. 이 때 C는 개인적으로 설정할 수 있는 값이며 C의 크기에 따라 model의 parameter 개수가 달라집니다. 성능이 변하는 것이죠. 그렇기에 학습하는 데이터셋의 크기를 고려해서 적절한 C를 정해야 합니다.

C는 image patch에 전혀 영향을 받지않는 값이며 MLP-Mixer의 연산 복잡도는 Image의 크기에 비례해 선형적으로 증가합니다. 같은 image patch를 사용할 때 크기가 (2K, 2K)인 이미지에서 나오는 patch의 개수는 (K, K)인 이미지에서 나오는 patch의 개수보다 4배 많아지며 이는 곧 token의 개수가 4배 많아지는 것이기 때문이죠.

구현은 꽤 쉽습니다. Linear layer 하나만 쓰면 해결됩니다.

projection_layer = nn.Linear(input_size[-3] * patch_size * patch_size,  C)

y = self.projection_layer(x)

코드를 보면 아시겠지만 연산이 너무 간단합니다. 그리고 2.1의 연산도 간단했기 때문에 저는 이 두가지 과정을 다음과 같이 하나의 클래스에다 구현했습니다.

class Per_patch_Fully_connected(nn.Module) :
    def __init__(self, input_size, patch_size, C) :
        super(Per_patch_Fully_connected, self).__init__()

        self.S = int((input_size[-2] * input_size[-1]) / (patch_size ** 2))
        self.x_dim_1_val = input_size[-3] * patch_size * patch_size
        self.projection_layer = nn.Linear(input_size[-3] * patch_size * patch_size,  C)

    def forward(self, x) :
        x = torch.reshape(x, (-1, self.S, self.x_dim_1_val)) 
        return self.projection_layer(x)

2.3 Token을 Mixer Layer에 넣기

MLP-Mixer의 핵심적인 부분입니다. 그러니 Mixer Layer에 대해 자세히 살펴보고자 합니다.
우선 Mixer Layer의 구조는 다음과 같습니다.

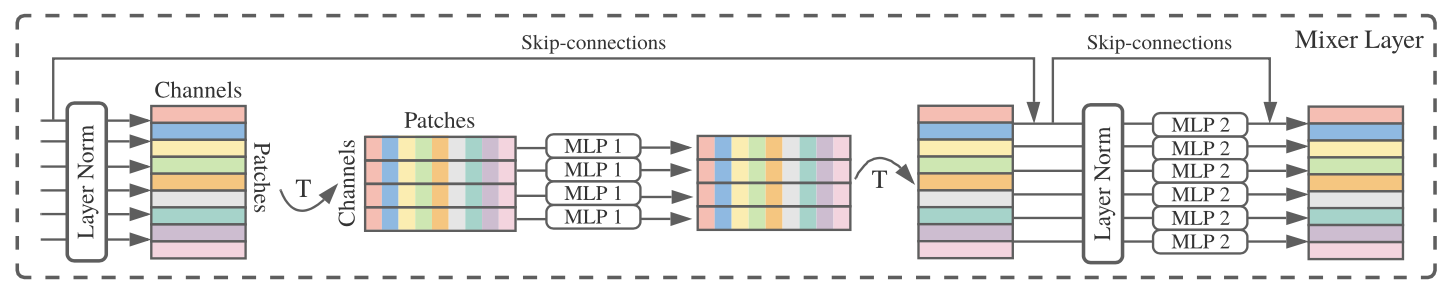
하나씩 살펴보겠습니다.

token-mixing MLP block

우선 S개의 C차원 token에 관한 연산을 수행합니다. token은 각 지역에서 얻은 값들을 가지고 만든 것이기 때문에 token-mixing MLP block의 역할은 각 영역의 정보를 가지고 연산한다고 볼 수 있겠습니다. 논문에서는 'allow communication between different spatial locations'이라고 나타냅니다.
위 그림에서 'token-mixing MLP block'의 범위는

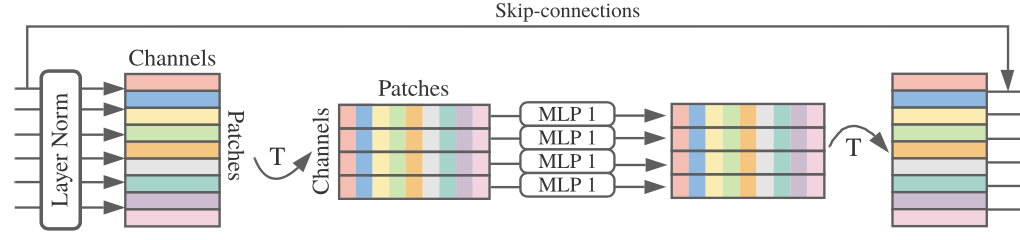
이부분입니다. 여기서 진행되는 연산의 순서는 다음과 같습니다.

1. Layer Norm : token별로 normalizaton을 수행합니다.
2. Transpose : [S x C] 행렬을 [C x S] 행렬로 만들어줍니다.
3. MLP : 서로 다른 token들의 요소들이 모인 C개의 S차원 벡터를 MLP에 넣어줍니다. 즉, [첫 번째 token의 n 번째 값, 두 번째 token의 n 번째 값...마지막 token의 n 번째 값]을 입력값으로 하여 MLP에 넣는 것이죠. 저자는 이 때 MLP의 구조를 따로 설계했는데요, 다음과 같습니다.
   
   여기서 GELU는 Gaussian Error Linear Unit의 약자로 ViT 등 attention mechanism을 사용하는 네트워크에 사용되었던 활성화 함수입니다.
   
   input = 0 부근에서 스무스하게 변하는 것을 확인할 수 있습니다.
   아무튼 MLP의 구조는 이러하며 특이한 점은 이 때 크기의 변화가 없다는 겁니다. 즉, [C x S] 행렬을 입력으로 받아 [C x S] 행렬을 출력하는 것이죠.
4. Transpose + skip connection : 출력한 [C x S] 행렬을 transpose하여 [S x C] 행렬로 만듭니다. 그리고 skip connection을 수행합니다.

이를 구현한 코드는 다음과 같습니다. 원래 하나씩 설명하려고 했는데 그렇게 하면 너무 길어지고 꼬이는 느낌이 들까봐 한 번에 구현코드를 보여드리고자 합니다.

class token_mixing_MLP(nn.Module) : 
    def __init__(self, input_size) : 
        super(token_mixing_MLP, self).__init__()

        self.Layer_Norm = nn.LayerNorm(input_size[-2]) # C개의 값(columns)에 대해 각각 normalize 수행하므로 normalize되는 벡터의 크기는 S다. 
        self.MLP = nn.Sequential(
            nn.Linear(input_size[-2], input_size[-2]),
            nn.GELU(),
            nn.Linear(input_size[-2], input_size[-2])
        )

    def forward(self, x) :
        # layer_norm + transpose
        
        # [S x C]에서 column들을 가지고 연산하니까 Pytorch의 Layer norm을 적용하려면 transpose 하고 적용해야함. 
        output = self.Layer_Norm(x.transpose(2,1)) # transpose 후 Layer norm -> [C x S] 크기의 벡터가 나옴
        output = self.MLP(output)

        # [Batch x S x C] 형태로 transpose + skip connection
        output = output.transpose(2,1)

        return output + x

channel-mixing MLP block

token에 대하여 연산을 끝낸 [C x S] 행렬은 이제 channel에 대한 연산을 수행합니다. 같은 지역에서 얻은 값들 사이의 관계를 가지고 연산을 수행하는 것이죠.
위 그림에서 channel-mixing MLP block의 범위는 다음과 같습니다.

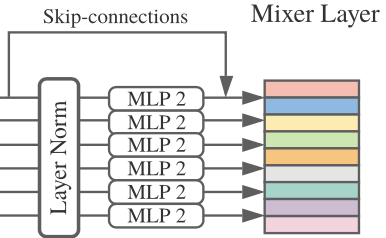
비교적 간단해보이지만 transpose를 하지않는 것 외에는 차이가 없습니다. 즉, 연산 과정이 token-mixing MLP block과 큰 차이가 없으며 가장 눈에 띄는 차이는 Layer Norm을 channel 단위, 다시 말해 token 내부의 값들끼리 normalize를 하고 MLP에 token 단위로 값을 넣는 것입니다.

구현 코드는 다음과 같습니다.

class channel_mixing_MLP(nn.Module) :
    def __init__(self, input_size) : # 
        super(channel_mixing_MLP, self).__init__()

        self.Layer_Norm = nn.LayerNorm(input_size[-1]) # S개의 벡터를 가지고 각각 normalize하니까 normalize되는 벡터의 크기는 C다

        self.MLP = nn.Sequential(
            nn.Linear(input_size[-1], input_size[-1]),
            nn.GELU(),
            nn.Linear(input_size[-1], input_size[-1])
        )
    
    def forward(self, x) :
        output = self.Layer_Norm(x)
        output = self.MLP(output)

        return output + x

Mix Layer

그러면 이 둘을 합친 Mix Layer는 다음과 같이 구현할 수 있겠습니다. 후에 MLP-Mixer를 만들 때 Mix Layer를 N층으로 쌓습니다.

# input_size : [Batch, S, C] 크기의 벡터
class Mixer_Layer(nn.Module) :
    def __init__(self, input_size) : # 
        super(Mixer_Layer, self).__init__()

        self.mixer_layer = nn.Sequential(
            token_mixing_MLP(input_size),
            channel_mixing_MLP(input_size)
        )
    def forward(self, x) :
        return self.mixer_layer(x)

2.4 Global Average Pooling

Mix Layer에서 얻은 값을 우리가 아는 MLP(=Linear layer)에 넣기 전에 Global average Pooling을 수행합니다. 그런데 여기서 말하는 Global Average Pooling은 파이토치에 내장되어있는 함수와는 조금 다릅니다. 저자는 Appendix E에서 다음과 같이 Pooling을 구현했습니다.

그래서 저는 다음과 같이 Global Average Pooling을 구현했습니다.

global_average_Pooling_1 = nn.LayerNorm([S, C]) # S, C 모든 측면에 대해 Normalize 수행

x = global_average_Pooling_1(x)
x = torch.mean(x, 2) # [S, C] 행렬에서 각 C개의 값끼리 평균  구함 -> [S,1] 행렬 휙득

2.5 MLP-Mixer 구현

그러면 이제 MLP-Mixer를 구현해봅시다.
앞에서 구현한 것들을 한데 모아서 만든 MLP-Mixer는 다음과 같이 구현할 수 있겠습니다.

# MLP-Mixer
# Per_patch_Fully_connected, token_mixing_MLP, channel_mixing_MLP로 구성됨
# input_size : 입력할 이미지 사이즈. (Batch, C, H, W) 양식이다. 예를 들면 (1, 3, 224, 224). (3, 224, 224) 크기의 데이터로 넣어도 된다
# patch_size : 모델이 사용할 patch의 사이즈. 예를 들어 16 
# C : desired hidden dimension. 예를 들어 16
# N : Mixer Layer의 개수
# classes_num : 분류해야하는 클래스의 개수
class MLP_Mixer(nn.Module) :
    def __init__(self, input_size, patch_size, C, N, classes_num) : 
        super(MLP_Mixer, self).__init__()

        S = int((input_size[-2] * input_size[-1]) / (patch_size ** 2)) # embedding으로 얻은 token의 개수

        self.mlp_mixer = nn.Sequential(
            Per_patch_Fully_connected(input_size, patch_size, C)
        )
        for i in range(N) : # Mixer Layer를 N번 쌓아준다
            self.mlp_mixer.add_module("Mixer_Layer_" + str(i), Mixer_Layer((S, C)))
        
        # Glboal Average Pooling
        # Appendix E에 pseudo code가 있길래 그거 보고 제작
        # LayerNorm 하고 token별로 평균을 구한다
        self.global_average_Pooling_1 = nn.LayerNorm([S, C])

        self.head = nn.Sequential(
            nn.Linear(S, classes_num),
            nn.Softmax(dim=1)
        )

    def forward(self, x) :

        if len(x.size()) == 3:
            x = torch.unsqueeze(x, 0) # 4차원으로 늘려줌.

        output = self.mlp_mixer(x)
        output = self.global_average_Pooling_1(output)
        output = torch.mean(output, 2)

        return self.head(output)

3. Experiment

다음으로 실험에 대한 설명을 간단히 해드리도록 하겠습니다.

저자가 수행한 실험과 제가 수행한 실험 두가지 모두 설명해 드리도록 하겠습니다

3.1 논문에서 나온 실험

우선 논문에 나온 실험, 다시말해 저자가 수행한 실험을 설명해드리도록 하겠습니다.

저자는 사전학습을 수행 후 특정 dataset을 가지고 fine-tuning을 수행했습니다. 사전학습은 구글이 내부적으로 소유하고있는 JFT-300M과 기존에 많이 쓰인 ImageNet, ImageNet-21k을 가지고 진행했습니다. 이 때 data augmentation도 수행했다고 합니다.

ImageNet은 분별해야할 클래스의 개수가 너무 많고 해당 객체의 사진이 특정 모습만 찍은게 아니라 다양한 모습을 찍었기 때문에 데이터셋'만' 가지고는 높은 성능을 갖게끔 학습시키는게 많이 힘듭니다. 그래서 Augmentation 기법을 필수로 해야 원하는 성능을 얻을 가능성이 높습니다.

fine-tuning은 CIFAR-10, CIFAR-100, Flowers, Pets, VTAB-1k 데이터셋에서 수행했다고 합니다.

실험 결과

실험에 참가한 네트워크들의 성능을 정리한 결과는 다음과 같습니다.

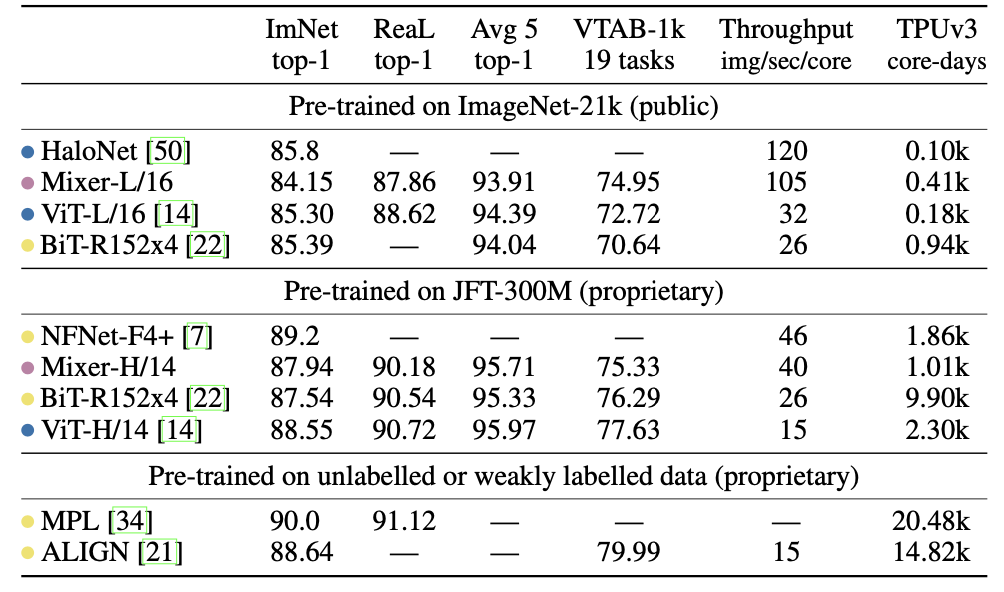
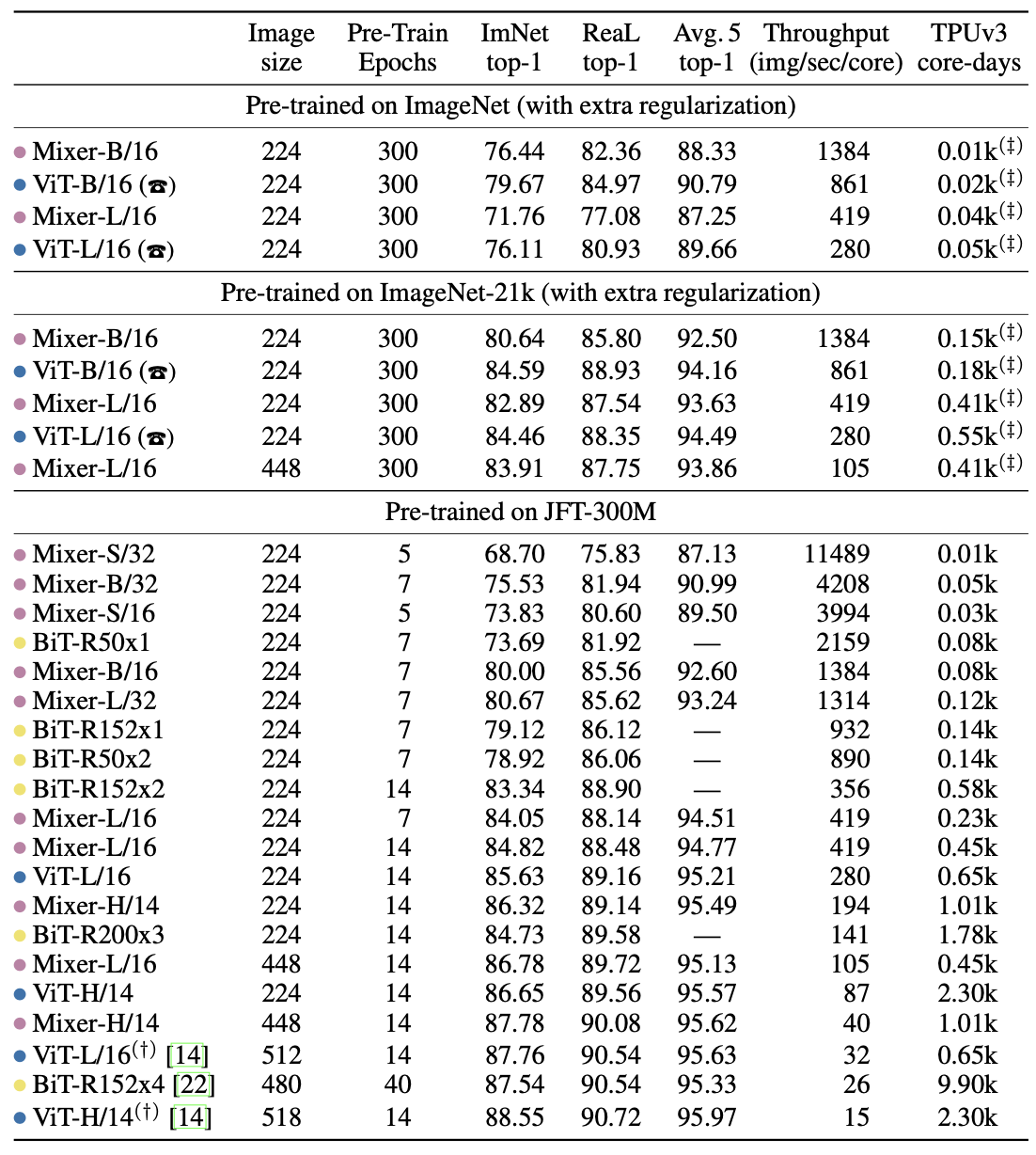
표에 나온 항목들을 간단히 정리해보겠습니다.

네트워크

1. Mixer : MLP-Mixer를 말합니다. Mixer 뒤에 S, B, L과 16, 32 이 있는데 여기서 S(small), B(base), L(large), H(huge)는 네트워크의 크기를 말하는 것이고 16, 32 등의 숫자는 Image Patch를 나타냅니다. 다음 표를 보시면 Mixer-B/16 등이 어떤 네트워크를 의미하시는지 이해하실 수 있을 것이라 생각됩니다.
   

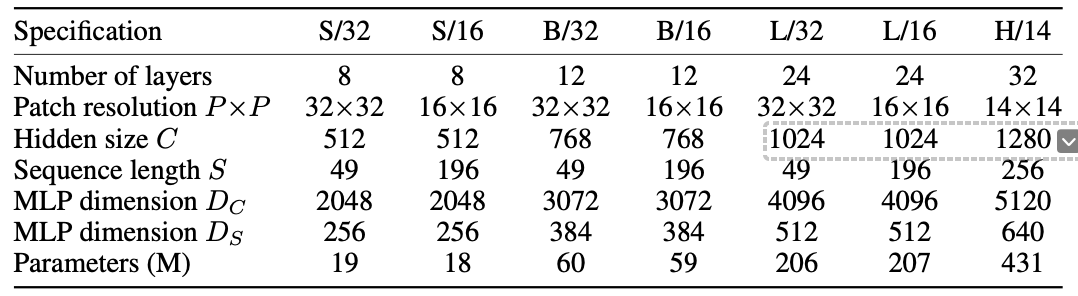
2. ViT : Vision Transformer를 나타냅니다. MLP-Mixer는 attention mechanism과 Convolutional neural network같은 방식들로 대부분의 네트워크를 만드는 현 상황에서 새로운 방식을 제안한 네트워크입니다. 그래서 성능 비교를 위해 실험에 attention mechanism을 사용한 네트워크의 대표라고 할 수 있는 ViT를 사용한 것으로 생각됩니다.

3. BiT : Big Transfer를 나타냅니다. BiT는 사전학습에 관한 논문인데요, 특이한 점은 새로 제안한 방식은 없고 기존에 있던 방식 중 SOTA를 달성하지 못한 방식을 조합해 '사전학습' 기법을 제작, ResNet을 학습시켜 SOTA를 달성했다는 겁니다. 즉, 실험에 ResNet을 사용했습니다. 표를 보시면 BiT-R152x1, BiT-R152x2, BiT-R152x3이 있는데요, 여기서 R은 ResNet, 152는 Convolutional neural network의 층, x1, x2, x3은 네트워크의 사이즈를 나타냅니다. 숫자가 클 수록 사용하는 parameter의 개수가 많습니다.

그 외 단어들 몇가지

1. Throughput : 처리량을 나타냅니다. 여기서는 1초당 이미지 처리량을 코어 단위로 표시한 것으로 보입니다. 클 수록 좋으며 크기가 작은 모델일 수록 초당 코어별 처리량이 높은 것을 확인할 수 있습니다.
2. TPUv3 core-days : 저자는 네트워크의 학습을 TPU 중 하나인 TPUv3에서 진행했으며 학습 시간과 학습에 사용된 코어의 개수를 곱한 값을 'TPUv3 core-days'라고 정의했습니다. 작을 수록 학습에 들인 자원이 적다는 뜻입니다.

실험을 통해 알 수 있었던 점

저는 위 결과를 통해 MLP만 가지고도 SOTA를 달성할 수 있겠다고 생각했습니다. 비록 모델의 크기를 최대로 키웠을 때 ViT에 밀리긴 하였으나 그 수치가 크지 않으며 MLP-Mixer는 '가능성'을 보여주는 첫 번째 제안이었기에 앞으로 더 좋은 방식이 제안되지 않을까 기대해봅니다. 그리고 성능이 비슷한 두 모델을 비교했을 때

ViT의 학습시간이 Mixer보다 훨씬 많다는 것(2.30k vs 1.01k)을 알 수 있습니다. 이를 통해 Mixer가 특정 성능으로 수렴하는 속도가 빠른 네트워크임을 알 수 있습니다.

3.2 제가 진행한 실험

다음으로 제가 진행한 실험을 간단히 소개해드리도록 하겠습니다.

네트워크 선정

저는 총 6가지의 네트워크를 사용했습니다.

1. normal_cnn : 일반적 방식으로 설계된 Convolutional Neural Network(CNN)입니다.
2. residual_cnn : Residual block을 이용해 설계된 CNN입니다.
3. mlp-mixer : MLP-Mixer입니다. 크기에 따라 S, B로 나뉘며 Image Patch는 (2,2)와 (4,4)를 사용했습니다.

모델의 parameter 개수는 다음과 같습니다.

model	parameter_num
normal_cnn	1,183,322
residual_cnn	1,134,026
mlp_mixer_S4	273,674
mlp_mixer_S2	1,062,026
mlp_mixer_B4	698,186
mlp_mixer_B2	1,756,106

실험 결과

사전학습 없이 CIFAR-10으로 학습시켰을 때 성능을 에포크별로 측정하였습니다. 측정한 항목은 Train Loss, Train Accuracy, Test Loss, Test Accuracy이며 결과는 다음과 같습니다.

Train

대체로 안정적인 수렴을 보여줍니다.

Test

조금 흔들리긴 하지만 그래도 수렴점으로 무난히 가는 모습을 보입니다.

실험을 통해 느낀 것

실험을 수행하며 제가 느낀 것을 정리하면 다음과 같습니다.

1. 실험의 규모가 작았다 : 학습에 사용한 데이터셋과 네트워크의 parameter 개수가 매우 작았습니다. 그래서 residual_cnn이 자신의 강점(깊은 레이어까지 gradient를 전달할 수 있다)을 제대로 보여주지 못했습니다.

2. mlp-mixer가 parameter 대비 성능이 좋다 : 가장 크기가 작은 mlp_mixer_S4와 normal_cnn의 parameter 개수 차이는 약 4.32배입니다. 그런데 성능 차이는 그리 크지않습니다. 제가 실험을 진행하며 제일 놀란 부분입니다. 그리고 제가 이 실험에 사용한 세팅(학습률, epoch 등)이 normal_cnn에 가장 적합했기 때문에 normal_cnn이 제일 높은 성능을 보여줬다고 생각되며 네트워크별로 가장 적합한 학습 세팅을 수행 후 학습을 진행했으면 다른 결과가 나왔을 것이라 생각합니다.

4. Conclusions

논문에 매우 다양한 내용이 있지만 저는 다 건너뛰고 conclusion을 말씀드리고자 합니다.

저자는 앞서 말씀드렸듯 기존의 CNN, attention mechanism 대신 MLP'만' 사용하여 매우 단순한 계산만 가지고 SOTA를 달성한 네트워크들과 경쟁할 수 있는 네트워크를 제안했습니다.

첫 시도에서 SOTA에 근접한 성능을 보여줬다는 것은 정말 큰 성과라 생각되며 더 심도있는 연구를 통해 기존의 방식들을 뛰어넘어 SOTA를 달성할 수 있는 네트워크가 제안되기를 기대합니다.

마지막으로, 저자는 vision 외에 NLP 등의 다른 domain에도 MLP만 사용하는 방식을 제안하는 것이 흥미롭겠다고 말했는데 이 역시 기대가 되는 부분입니다.

---

후기

오랜만에 논문 리뷰를 진행했습니다. 실험도 진행한다고 꽤 오래 걸렸습니다. 원래 오래 걸릴 일이 아닌데 제가 실험을 하다가 삽질을 자꾸 해서 오랜 시간이 걸렸습니다.

원래 ImageNet을 가지고 진행하려고 했는데 데이터셋의 용량이 너무 커서 데이터셋의 일부만 가지고 학습해야했으며 데이터셋을 구현할 때 data augmentation을 진행하는 부분을 구현하지 않아 학습이 제대로 진행되지 않았습니다. 이 과정에서 data augmentation의 중요성을 실감할 수 있었죠.

그래서 data augmentation을 구현해야겠구나 마음 먹었는데...너무 긴 학습시간이 마음에 걸렸습니다. 대략적으로 계산해보니 6개 네트워크를 어느정도 학습시키려면 한 달은 걸린다는 결론이 나왔죠. 결국 크기가 작은 CIFAR 데이터셋으로 변경했습니다. 데이터셋의 크기도 작고 분류할 객체의 개수도 적고 각 객체의 이미지들이 객체별 특성이 잘 드러나게 나와있어 학습이 쉬웠습니다.

아주 완벽한 실험은 아니었지만 제가 직접 실험 세팅을 하여 실험을 하여 나름의 결과가 나왔기 때문에 매우 만족스러운 실험이었습니다. 이번 실험을 통해 많은 자체 피드백을 거쳤기에 다음 실험에서는 더 완성도 높은 실험을 수행할 수 있을 것으로 생각됩니다.

요즘 논문을 많이 읽고 있는데 리뷰를 하는건 다른 문제라는 사실을 계속해서 깨닫고 삽니다. 그래도 이렇게 리뷰를 진행할 정도로 논문을 꼼꼼히 읽고 가능하다면 구현을 해보는 경험이 정말 귀중하다고 생각되기에 시간이 날 때마다 리뷰를 해보도록 하겠습니다.

긴 글 읽어주셔서 감사합니다. 다음 논문에서 뵙겠습니다.