[논문리뷰] FEDPARA- LOW-RANK HADAMARD PRODUCT FOR COMMUNICATION-EFFICIENT FEDERATED LEARNING

안녕하세요. 밍기뉴와제제입니다. 이번에 리뷰할 논문은 FEDPARA- LOW-RANK HADAMARD PRODUCT FOR COMMUNICATION-EFFICIENT FEDERATED LEARNING입니다. 이 논문은 기존의 네트워크보다 적은 parameter를 가지고도 비슷하거나 더 좋은 성능을 내게끔 하는 연산 방식인 Fedpara를 제안하였습니다. (네트워크의 연산법 + parameter 설정법)을 제안하는 논문이라고 보시면 될듯 합니다.

그러면 지금부터 논문 리뷰를 시작해보겠습니다.

1. INTRODUCTION

저는 이 논문을 읽으면서 Federated learning이라는걸 처음 알았습니다. 우리말로 '연합학습'이라 불리는 Federated learning은 모델의 학습을 하나의 기기가 아니라 여러대의 기기에서 각자의 데이터로 학습하는 방식을 말합니다.

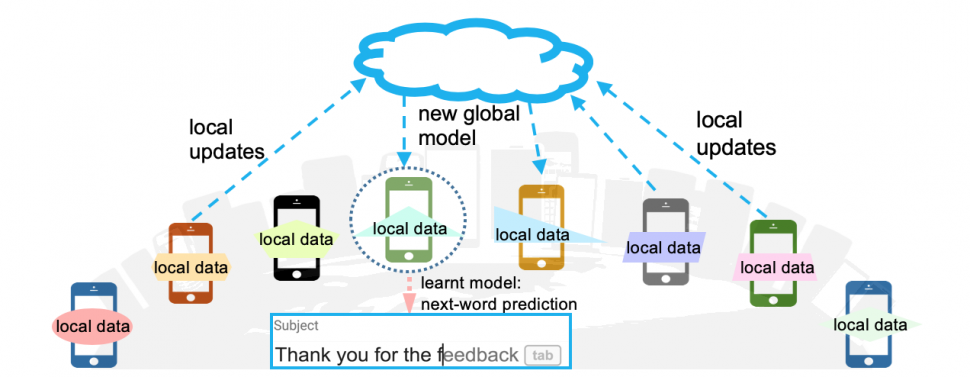
Federated learning을 표현한 그림. 클라우드에 global model이 저장되어 있고 각 기기에서 각자 가지고 있는 데이로 global model를 학습시킵니다. 이미지 출처

위와 같은 방식으로 모델을 학습시키면 데이터 공유 없이 각자의 개인적 특징이 담긴 데이터로 모델을 학습시킬 수 있다는 장점이 있습니다. 기존의 방식대로 학습시키면 모든 데이터를 하나의 기기에 모아야하는데 이 과정에서 개인정보 등이 유출될 수 있으나 Federated learning는 각자의 기기에서 모델을 학습시킬 수 있기 때문에 그러한 위험성을 막을 수 있는 것이죠.

Federated learning은 여러 기기에서 학습을 진행한다는 점에서 Distributed learning와 비슷한 측면이 있습니다. 허나 두 학습방식은 다음과 같이 2가지 측면에서 차이가 납니다.

1. Heterogeneous data : 하나의 데이터셋을 가지고 여러 기기에서 모델의 학습을 나눠 진행하는 Distributed learning과는 달리 Federated learning은 각 기기에서 보유하고 있는 데이터를 가지고 모델을 학습합니다. 즉, 데이터들이 탈중앙적(decentralized)이고 독립항등분포가 아니며(non-IID) 각 기기가 가지고 있는 데이터들의 크기가 서로 다릅니다. 저는 이를 각자의 휴대폰에 가지고 있는 사진의 분포와 개수가 다른것으로 이해했습니다.

2. Heterogeneous systems : 하나의 기기에서 여러 gpu로 모델을 학습시키는 Distributed learning와는 달리 Federated learning는 학습에 사용하는 기기들(휴대폰 등)은 서로 성능이 완전 같기가 힘듭니다. 모두가 같은 기기를 갖고 있지 않기 때문이죠. 학습에 사용하는 기기들의 성능이 매우 다양할 것입니다. 그리고 global model을 다운로드 받고 학습을 진행해야 하는데 이 때 인터넷 성능에 따라 다운로드 받는 시간, 성공 여부, 학습시킨 parameter들이 global model에 반영되는 시간 등 다양한 요소들이 각기 다를 것이며 학습에 참여하는 기기가 많아질 수록 모델을 다운로드/업로드할 때 생기는 통신량이 많아져 네트워크에 큰 부담을 주게 됩니다.

위의 2가지 측면을 통해 Federated learning이 가지는 문제점을 확인할 수 있습니다.

개선방법 찾기

사람들은 앞서 언급한 Federated learning의 단점을 해결하기 위한 방법을 찾고자 노력했습니다. 다양한 기기에 있는 Heterogeneous data를 사용하고 통신에 많은 에너지를 사용(communication overheads)해야하는 환경에서 학습 곡선이 안정적으로 수렴하게 만들길 원했죠. 사람들은 Federated learning의 안정성을 높히고 communication rounds를 줄이기 위해 다양한 노력을 했으며 그 중 하나가 바로 '전송하는 데이터의 크기를 줄여보자'입니다. 모델을 전송할 때 사용하는 에너지량이 계산할 때 사용하는 에너지량보다 훨씬 많았기 때문에 우선적으로 개선을 해야만 하는 요소라고 볼 수 있습니다. loss function이나 model aggregation methods를 바꾸는 등 여러 방식을 제안하였으나 여전히 전송되는 데이터의 크기가 많았습니다. 새로운 해결책이 필요합니다.

FedPara

그래서 저자는 새로운 해결책을 제안했습니다. 모델의 구조가 아닌 모델의 Parameter 조정에 기여하는 요소들을 바꾸는 이전 방식들과는 달리 '모델의 Parameter 개수'를 변경하는 방식을 제안하였으며 그 이름을 FedPara라고 하였습니다.

FedPara는 '모델의 성능을 보존하며 Parameter 개수를 줄이는' 장점을 가지고 있습니다. 보통 Parameter의 개수가 줄어들면 성능도 줄어드는데, 참으로 신기하지 않을 수 없습니다. 논문에 의하면 Fedpara는
low-rank parameterization와 Hadamard product를 결합한 low-rank Hadamard product를 이용하였기 때문에 이러한 장점을 지닐 수 있다고 나옵니다. 식으로 표현하면

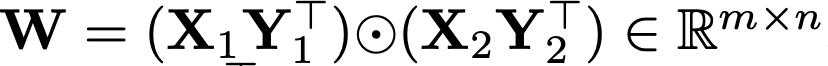
이러합니다. 식에 대한 자세한 설명은 2장 Method에서 나오니 지금은 식이 이렇게 생겼다는 것만 보여드리고 넘어가겠습니다. 위와 같은 방식으로 Parameter를 구성하고 연산을 하게되면 Parameter 개수를 줄이지 않는 기존 모델들이 가지는 성능과 비슷한 성능을 보여줄 수 있습니다. 이 역시 나중에 자세히 소개되기 때문에 간단히 하고 넘어가도록 하겠습니다.

Hadamard product

한글로 '아다마르 곱'이라 불리는 이 연산은 'element-wise product'와 같은 의미를 지닙니다.

이미지 출처

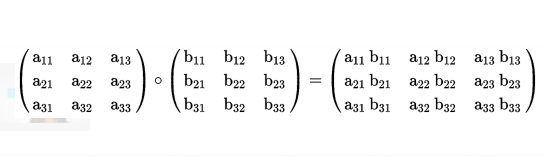
수학기호로 나타내면 ⊙이며 파이썬 코드로는 numpy.multiply()를 사용해 구현할 수 있습니다.

Fedpara는 Parameter의 개수를 줄였기 때문에 모델을 다운로드/업로드 할 때 발생하는 통신량이 많이 줄어듭니다. 에너지 소모를 많이 줄일 수 있는 것이죠. 그리고 주의해야될 점은, Fedparar가 Parameter 개수랑 연산 방식만 변경했으며 loss function같은 요소들은 변경하지 않았다는 것입니다. 오로지 '각 레이어의 내부 구조'만 변경하는 방식이죠.

실험결과는 꽤 만족스럽습니다.Fedpara나 기존 방식으로 만든 VGG, LSTM 등의 네트워크를 테스트 해봤는데요, 모두 Fedpara를 가지고 만든 모델이 더 성능이 비슷하거나 더 좋음을 확인할 수 있었습니다. 이는 3. EXPERIMENTS에서 제대로 나오니 여기선 간단히 설명해 드리도록 하겠습니다.

pFedpara

저자는 Fedpara에서 Federated learning의 개인화를 더 강조한 pFedpara도 제안했습니다. Federated learning에서 개인화란 global model을 각자의 상황에 맞게 학습하여 사용할 수 있는 정도를 말합니다. pFedpara는 모델에 있는 Parameter들을 global하게 학습하는 Parameter와 개인적으로 학습시키고 사용하는 Parameter로 분류하였습니다. 이렇게 Parameter들을 두종류로 나눠 학습한 결과, 더 좋은 성능이 나오는데다 더욱 robust한 모습을 보여줬다고 합니다. 추후 자세히 설명드리겠습니다.

지금까지 Federated learning의 '통신과정에 발생하는 과도한 에너지 소모'를 해결하고자 low-rank parameterization와 Hadamard product를 결합한 low-rank Hadamard product를 사용해 모델이 사용할 Parameter 개수를 줄이면서 성능을 유지하는(오히려 더 좋아질 수도 있는) Fedpara와 개인화를 강화한 pFedpara에 대해 간단히 알아봤습니다. 다음장부터 본격적으로 FedPara와 pFedPara에 관해 알아보도록 하겠습니다.

2. METHOD

Fedpara와 pFedpara에 관한 자세한 설명이 적혀있는 장입니다.
우선 low-rank parameterizations 중 유명한 3가지 방식과 FedPara의 성능을 비교하고(2.1) FedPara의 알고리즘적 요소를 알아본 뒤(2.2) pFedPara에 대해 자세히 알아보도록(2.3) 하겠습니다.

2.1 OVERVIEW OF LOW-RANK PARAMETERIZATION

low-rank parameterization은 쉽게 말해 모델의 Parameter 개수를 줄이는 방식입니다. Parameter 개수가 줄어들기 때문에 용량이 가벼워진다는 장점이 있으나 Parameter 개수가 줄어들었기 때문에 성능의 감소를 피할 수 없었습니다.
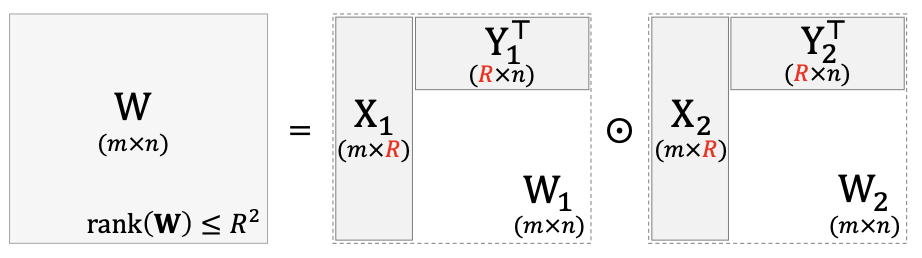
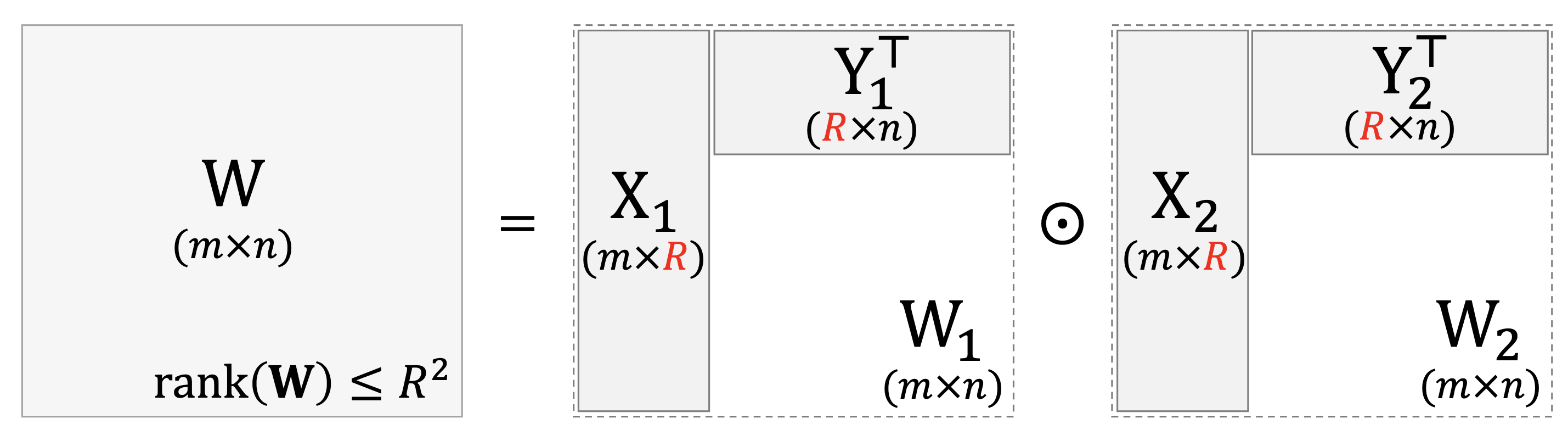
우선 low-rank parameterization에 대해 간단히 설명해드리도록 하겠습니다. low-rank parameterization은 W ∈ [m×n]과 X*Transpose(Y) = W~ ∈ [m×n]이 있을 때 W - W~를 최소화 하는 X ∈ [m x r]과 Y ∈ [n x r]의 r<< min(m, n)을 구하는 방식이라 보시면 되겠습니다. 제가 설명을 잘 못해서 논문 속 설명도 같이 첨부하도록 하겠습니다. 아래 구문에서 밑줄친 부분이 low-rank parameterization에 관한 설명입니다.

low-rank parameterization을 사용하면 행렬 W의 복잡도가 O(mn)에서 O((m+n)r)로 줄어들며 최적의 r은 SVD으로 찾을 수 있다고 합니다.

지금까지 low-rank parameterization을 간단히 알아봤습니다. 딥러닝에서는 Fully connected 레이어나 Convolutional 레이어에 적용해 Parameter의 개수를 줄이는데 사용하며 이러한 low-rank parameterization을 conventional low-rank constraints나 low-rank parameterization methods로 부른다고 합니다.

앞서 Federated learning이 통신중에 발생하는 에너지나 연산량이 많다고 말씀드렸습니다. 그렇기 때문에 low-rank parameterization을 사용하면 Parameter 개수가 줄어들고 그로 인해 주고받을 데이터의 크기도 줄어들죠. 이는 Federated learning에서 굉장히 중요한 일입니다. 이전 방식에서 low-rank parameterization을 사용하긴 했으나 이는 학습이 다끝난 Parameter를 줄이기 위해 low-rank parameterization한 경우였습니다. 전송되는 Parameter의 크기를 줄이지않았기 때문에 통신량은 감소하지 않았던 것이죠.

허나 Fedpara는 다릅니다. '개수가 줄어든 Parameter'로 학습시키는 low-rank Hadamard product를 사용하기 때문에 Parameter를 전송할 때 통신량이 감소하는 효과를 얻을 수 있죠. Fedpara의 과정을 간단히 소개해드리면 다음과 같습니다.

1. global model을 저장한 곳에서 각 기기로 '학습 가능한 레이어의 Parameter개수가 줄어든' 모델을 전송
2. 각 기기에서 각자가 가진 데이터로 학습
3. 학습이 끝난 Parameter를 global model이 저장된 곳으로 전송

그러면 성능은 어떨까요? 논문에 의하면 Parameter 개수를 줄이기 전의 모델과 FedPara로 학습시킨 모델을 비교했을 때 비슷한 성능을 달성할 수 있었다고 합니다.

2.2 FEDPARA: A COMMUNICATION-EFFICIENT PARAMETERIZATION

앞서 설명해드린 low-rank parameterization methods는 Parameter의 개수를 줄이는데는 성공했으나 rank가 줄어들었기 때문에 W가 가질 수 있는 독립된 벡터의 개수가 줄어듭니다. 즉, 성능이 떨어진다는 것이죠.

저자는 Parameter의 개수도 줄이면서 성능은 유지하는 방식을 찾고 싶었고 성능 저하를 해결하기 위해 앞서 말씀드린 'low-rank Hadamard product parameterization', 다시 말해 FedPara를 고안했습니다.

그러면 지금부터 FedPara의 성질이 뭔지 알아보도록 하겠습니다. 허나 그전에 Hadamard product에 대해 간단히 설명해드리도록 하겠습니다.

성질 1 : [m x r1]크기의 행렬 X1과 [m x r2]크기의 행렬 X2, [n x r1]크기의 행렬 Y1과 [n x r2]크기의 행렬 Y2가 있고 r1, r2 <= min(m, n)일 때 Hadamard product로 만들어지는 행렬 W := (X1 x Transpose(Y1)) ⊙ (X2 x Transpose(Y2))의 rank는 rank(W) <= r1 x r2를 만족한다.
증명 : 여기서 X1 x Transpose(Y1)와 X2 x Transpose(Y2)는 독립적인 벡터가 하나밖에 없는 rank-1 행렬입니다. 달리 말하면 X, Y의 열(column) 벡터들의 행렬곱을 합친 행렬인 것이죠. 그러므로 W는

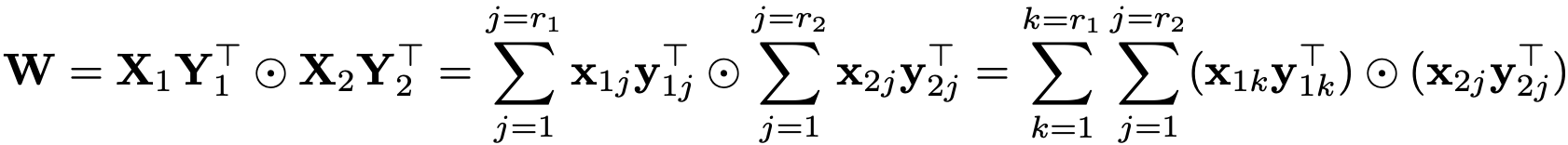
위 식의 오른쪽 항과 같이 rank가 1인 행렬을 r1 x r2개 합친 행렬이라고 볼 수 있으며 r1 x r2개의 행렬로 구성되었기 때문에 서로 독립인 벡터가 최대 r1 x r2개일 수 있습니다. 즉, 최대 r1 x r2의 rank를 가질 수 있는 것이죠.

성질 1을 통해 최대 2R의 rank를 가지는 W를 만들어내는 low-rank parameterization와는 달리 FedPara는 low-rank행렬 W1, W2를 Hadamard Produrct로 곱해 최대 R^2의 rank를 가지는 higher-rank matrix도 만들어낼 수 있다는 것을 확인할 수 있으며 만약에 r1과 r2의 값을 r1 x r2 ≥ min(m, n)을 만족하게끔 설정하면 W을 full-rank matrix도 만들 수 있습니다. 왜냐하면 최대로 도달 가능한 rank가 r1 x r2인데 r1 x r2 = min(m, n)이면 최대로 도달할 수 있는 rank가 full-rank라는 뜻이 되기 때문이죠.

다시말해, r1과 r2의 값을 r1 x r2 ≥ min(m, n)을 만족한다는 말은 최대로 도달할 수 있는 rank를 무조건 full-rank가 되게끔 설정한다는 의미로 해석할 수 있겠습니다.

논문에서는 이를 'FedPara는 full-rank에 도달할 수 있는 최소한의 parameter 성질을 가지고 있다'고 말합니다.

성질1을 그림으로 나타내면 다음과 같습니다.

W의 크기는 같은데 최대 rank가 다르다는 것을 확인할 수 있습니다.

그리고 r1, r2로 rank와 동시에 Parameter의 개수도 정할 수 있습니다. 즉, 성능과 용량을 동시에 만족시키는 최적의 r1, r2를 정해야 한다는 것이죠. 다행히도 가장 최적의 r1, r2를 선택할 수 있는 방법이 있으며 이는 FedPara의 두 번째 성질입니다. 논문에 의하면 '최소한의 parameter로 최대한의 rank를 가지는 방법'이죠.

성질 2 : r1=r2=R인 자연수 R은 다음 기준을 만족하는 '유일한' 최적값이다.

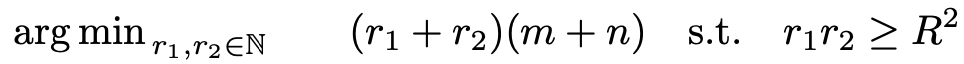
그리고 위 기준을 만족하는 최적의 값은 2R(m+n)이다.
증명 : 주어진 조건과 산술-기하 평균 부등식(arithmetic-geometric mean inequality)을 이용하여 다음의 부등식을 만들 수 있다.

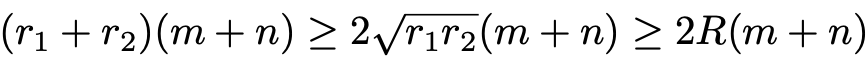
위 식은 산술-기하 평균 부등식에 의해 r1=r2=R일 때만 등식이 성립한다.

성질 2는 FedPara를 사용하는 모델이 이용할 W의 rank를 R^2로 설정했을 때 Parameter의 개수를 최소화하는 기준(criteria)을 나타낸 것입니다.(저자는 FedPara로 설계할 모델이 가지는 W의 rank를 R^2로 정했습니다.) 성질2 덕분에 우리는 FedPara를 사용할 때 최적인 r1, r2의 값을 쉽게 설정할 수 있습니다.

그리고 성질 1의 'r1과 r2의 값을 r1 x r2 ≥ min(m, n)을 만족하게끔 설정하면 W을 full-rank matrix도 만들 수 있다'도 이용해 r1=r2=R, R^2 ≥ min(m, n)인 r1, r2를 설정하면 full-rank인 W를 만들 수 있을 확률이 매우 높아질 것입니다. 최대 rank는 무조건 full-rank가 되기 때문이죠. 논문에 의하면 2R(m + n) << mn인 2R(m + n)을 사용해도 full-rank 행렬이 될 가능성이 높다고 하네요.

그러면 서로 같은 Parameter 개수를 가지고 FedPara로 생성한 W와 naive low-rank parameterization로 생성한 W의 rank는 얼마나 차이날까요? 다음 표를 통해 확인하실 수 있습니다.

Fully Connected 레이어와 Convolutional 레이어를 3가지 방식으로 만들었을 때 parameter 개수와 도달할 수 있는 최대 rank를 비교한 표입니다. Low-rank는 기존 방식보다 parameter 개수는 줄였으나 최대 Rank가 낮고 FedPara는 parameter 개수는 줄어들었으나 최대 랭크가 R^2라 R만 잘 고르면 기존 방식과 같은 Rank를 가질 수 있음을 확인할 수 있습니다.

지금까지 X*W = Y가 되는 Fully Connected 레이어에서 W를 정하는 방법을 알아봤습니다. 그러면 Convolutional 레이어는 어떻게 설계했을까요? 성질 1과 2의 FedPara를 이용한 경우에는 Fully Connected 레이어에 사용한 방식을 naive한 방식으로 Fully Connected 레이어에 적용하여 O×I×K1×K2형태의 4차원 텐서 커널을 O×(IK1K2) 형태로 변형하였습니다.

여기서 O : output channels, I : input channels, (K1, K2) : kernel sizes입니다.

이렇게 naive하게 적용해도 위의 표에서 보실 수 있듯 기존의 레이어보다 훨씬 적은 parameter 개수를 가지면서도 같은 랭크를 유지할 수 있었습니다. 허나 Low-rank로 만들었을 때와 비교했을 때 거의 4배에 달하는 parameter 개수를 가지고 있죠. 이는 'parameter 개수를 최소한으로 하며 최대한의 성능을 내는' FedPara의 목적에는 조금 부족한 성과라고 볼 수 있겠습니다.

그래서, 저자는 세 번째 성질을 도입해 Low-rank를 사용했을 때와 같은 parameter 개수를 가지면서도 기존 방식과 같은 rank를 가질 수 있게 되었습니다. 정말 대단한 일이죠.

Convolutional 레이어의 개수를 대폭 줄이면서도 성능을 유지할 수 있게 만든 세 번째 성질은 다음과 같습니다.

성질 3 : 크기가 [R×R×k3×k4]인 텐서 커널 T1, T2와 크기가 [k1×R]인 행렬 X1, X2, 크기가 [k2×R]인 행렬 Y1, Y2가 있고 R<=min(k1, k2)일 때 다음과 같은 convolution kernel W의 ranks는 rank(W(1)) = rank(W(2)) ≤ R^2를 만족한다.

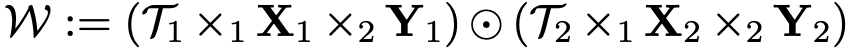
증명 : 우선 W(1), W(2)의 의미부터 알아보겠습니다. W(1), W(2)는 W의 첫 번째, 두 번째 unfolding이며 식으로 나타내면 다음과 같습니다. (여기서 I(3)은 [k3 x k3], I(4)는 [k4 x k4]크기를 가지는 단위 행렬( identity matrix))

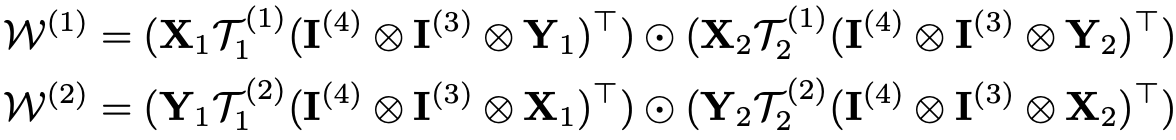
이들을 성질 1에서 W구하는 식으로 다시 구해보면 최대 rank가 R^2임을 확인할 수 있습니다. 그래서 성질 3이 성립합니다.

텐서 unfolding은 말 그대로 텐서를 '펼치는 것'을 뜻하며 그림으로 나타내면 다음과 같습니다.

이미지 출처
그리고 ⊗는 크로네커 곱(Kronecker product)을 나타내는 기호이며

위와 같은 성질을 가졌습니다. 이미지 출처

저자는 성질 3을 통해 FedPara를 reshaping없이 convolutional 레이어 설계에 사용할 수 있다고 말했습니다. 앞서 보여드린 표가 이를 증명하죠. 성질 1을 사용해 naive한 방식으로 만든 convolutional 레이어보다 약 3.8배 적은 parameter 수를 가지면서도 rank는 똑같은 레이어가 만들어지는 것을 확인할 수 있습니다.

저자는 여기에 더해 non-linearity and the Jacobian correction regularization도 사용해봤다고 하며 사용 결과, 정확도와 수렴 안정성이 증가하는 것을 확인했다고 합니다. 허나 필수적인 과정은 아니며 추가로 사용할 수 있는 리소스(vram같은 것으로 추측됩니다)가 있으면 사용하는 것을 권장하는듯 합니다. 논문에는 자세한 내용이 실리지 않았으나 supplementary에 자세한 내용이 실려있습니다.

2.3 PFEDPARA: PERSONALIZED FL APPLICATION

Federated learning을 실제로 사용할 경우, 사용량, 사용 성향 등 각 기기가 가지는 특징들이 서로 다르기 때문에 데이터들이 서로 다르며 개인적인 특징을 띄고 있습니다. 공동으로 학습한 모델이 특정 기기가 사용하는 환경에서 제성능을 못낼 때가 있을 수 있다는 뜻이죠.

그래서 앞서 연구된 FedPer은 이를 해결하기 위해 '공동으로 학습하는 레이어'와 '개인적으로 학습하는'레이어를 구분하는 방식을 고안했습니다. 각 기기는 각자의 데이터로 모델을 학습한 뒤 '공동으로 학습하는 레이어(global layer)'만 global model이 저장된 곳으로 보내고 '개인적으로 학습한'레이어(local layer)는 보내지 않는 것이죠. 그러니 global layer는 모든 기기에서 사용할 수 있는 'general features'를 추출하게끔 학습되고 local layer는 각 기기의 환경에 적합한 feature만 추출하게끔 학습됩니다.

그러면 저자가 만든 pFedPara는 어떨까요? FedPara의 개인화(personalization)를 강화한 pFedPara는 Hadamard product를 global inner weight W1과 local inner weight W2를 연결하는 다리로 사용합니다. pFedPara를 이용해 만든 레이어의 가중치 크기는 W = W1 ⊙ (W2 + 1)가 되며 학습중에 W1는 global model이 저장된 곳으로 전송하고 W2는 각 기기에만 저장합니다.

앞서 말씀드린 가중치를 구성하는 식 W = W1 ⊙ (W2 + 1)을 자세히 살펴봅시다. W1의 값에 따라 (W2 + 1)이 유효한 값이 될지 안될지 결정되는 것을 알 수 있습니다. 스위치 역할을 하는 것이죠. 저자는 'W1이 모든 기기가 공유하는 정보를 학습하게끔' 하기위해 이러한 가중치 식을 세웠다고 합니다.

그리고 W1이 서버로 보낼 가중치, 다시 말해 parameter들이므로 W의 식을 풀어서 쓰면 W1 ⊙ W2 + W1이 되며 저자는 W1 ⊙ W2 = W_per, W1 = W_global로 정의해 pFedPara로 설정되는 가중치를 'global weight W_global과 personalizing residue W_per이 결합된 값'이라 말했습니다.

FeaPara와 차이점

그러면 pFedPara와 FedPara의 차이점은 뭘까요? FedPara는 학습한 모든 parameter들만 업로드/다운로드하고 pFedParas는 global하게 사용할 레이어의 parameter들만 업로드/다운로드합니다.

즉, 통신량이 적어지는 것이죠. pFedPara는 FedPara에 비해 통신 효율이 더욱 좋아졌습니다.

FedPer과 비교

앞서 FedPer을 먼저 소개해드린 후 pFedPara를 소개해드렸습니다. 두 방식 모두 parameter를 두종류로 나눠 하나는 global하게 사용하고 나머지 하나는 각 기기에 맞게 local한 방식으로 사용합니다. 그러면 어떤 차이가 있는것일까요? 바로 'parameter를 구분하는 선'에 차이가 있습니다.

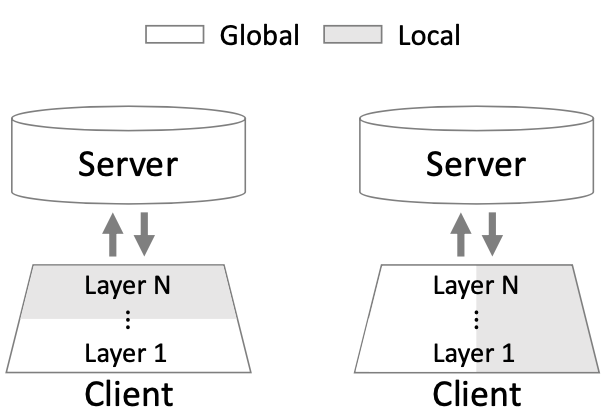
그리고 저자는 feed-forward network의 경우만 FedPara와 pFedPara를 설명했는데 다른 종류의 네트워크에도 FedPara와 pFedPara를 적용할 수 있다고 말했습니다.

지금까지 FedPara의 3가지 성질과 pFedPara에 관해 알아봤습니다. 적은 parameter로도 기존의 모델과 비슷한 성능을 낼 수 있다는게 정말 대단하다는 생각이 들었습니다. 다음장에서는 FedPara, pFedPara로 만든 모델과 다른 방식들로 만든 모델을 가지고 성능을 비교합니다.

3. EXPERIMENTS

성능을 측정하는 실험입니다. 저자는 FedPara를 다른 Federated method들과 communication costs, the number of parameters, and compatibility를 비교하였고 pFedPara를 non-IID scenario에서 어떠한 성능을 보여주는지 실험하였습니다. 그리고 compatibility experiments를 제외한 나머지 실험에서 FedAvg를 사용했다고 하네요.

3.1 SETUP

실험을 위해 준비한 것들을 설명하는 부분입니다.

Datasets

우선 데이터셋입니다. 저자는 FedPara, pFedPara를 가지고 실험할 때 사용한 데이터셋이 각각 다른데요, 하나씩 설명해드리겠습니다.

1. FedPara : FedPara를 가지고 실험할 때 사용한 데이터셋은 CIFAR-10, CIFAR-100, CINIC-10, subset of Shakespeare입니다. IID한 데이터셋 환경을 가정한 상황일 때는 CIFAR-10과 CINIC-10을 100등분, CIFAR-100을 50등분 하였고 non-IID한 상황에서는 디리클레 분포(Dirichlet distribution)를 사용해 랜덤한 개수로 등분하였으며 이 때 Dirichlet parameter α를 0.5로 설정했습니다. 이렇게 등분한 데이터셋은 학습에 참가하는 각 기기마다 하나씩 할당하였고 학습 중 매 라운드마다 16%의 기기를 샘플하였다고 합니다.
2. pFedPara : pFedPara와 함께 사용한 데이터셋은 MNIST, FEMNIST입니다. 그리고 non-IID한 환경에서는 학습에 참가한 100개의 기기가 최대 2종류의 클래스가 포함된 데이터셋을 갖게끔 데이터셋을 등분했습니다.

Models

저자는 실험에 사용한 CNN으로 VGG, ResNet을 사용하고 RNN은 LSTM, Fully connected 모델은 단순히 2개의 Fully Connected 레이어를 연결한 모델을 사용했습니다.
이 때 VGG는 배치 정규화 대신 group normalization를 사용했습니다. 그리고 총 3가지 방식으로 모델을 설계하고 비교하였는데요, 기존 모델은 '_ori', Tucker form에 맞춘 low-rank parameterization을 사용한 모델은 '_low', FedPara를 사용해 만든 모델은 '_FedPara'라는 수식을 추가하였습니다.

그리고 pFedPara로 실험을 할 때는 두 개의 Fully Connected 레이어를 연결한 모델을 사용했습니다.

Rank Hyper-parameter

저자는 레이어의 가중치 W를 구성하는 W1, W2의 rank를 r = (1−γ) x r_min + γ x r_max로 구성하였습니다. 여기서 r_min은 FedPara를 사용해 W가 full-rank matrix를 가지게끔 할 때 사용할 수 있는 최소한의 rank를 말하며 r_max는 FedPara를 사용하는 레이어가 가지는 parameter의 개수가 기존 방식으로 만들어진 레이어가 가지는 parameter의 개수를 초과하지 않게하는 최대 rank를 말합니다. 즉, γ을 사용해 모델이 가지는 parameter의 개수를 조정할 수 있는 것입니다.

3.2 QUANTITATIVE RESULTS

표와 그래프로 실험결과를 설명하는 부분입니다.

Capacity

여기서는 rank의 차이로 인한 성능 차이를 보여줬습니다. 저자는 Parameter의 수를 같게 하고 Low-rank parameterization과 FedPara로 VGG16과 LSTM을 설계하고 Federated learning으로 학습 후 성능을 비교해봤는데요, 다음과 같았습니다.

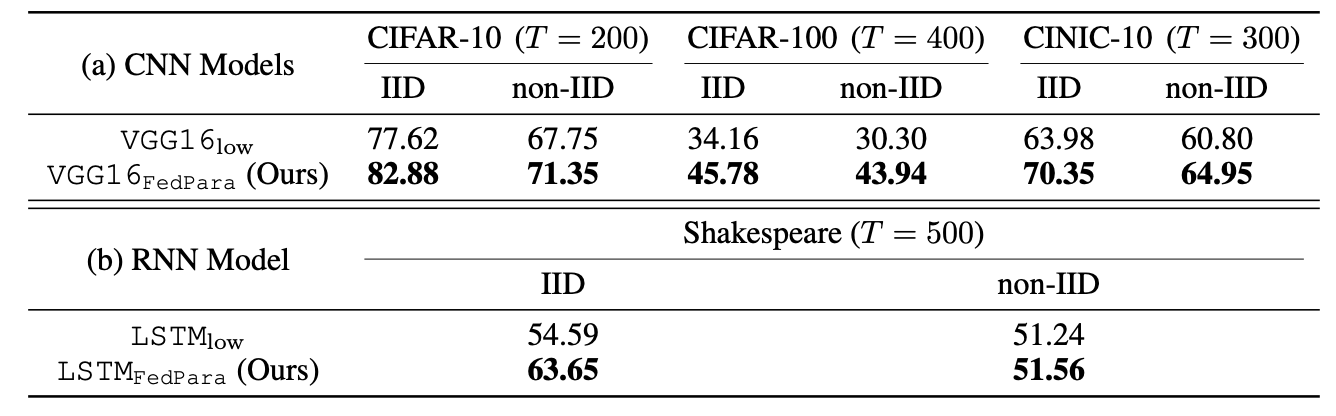
위의 표에서 T는 모델을 학습시키기 위해 global model이 저장된 서버와 업로드/다운로드를 수행한 횟수입니다. 논문에서는 이를 'round'라고 표시했습니다.

표에도 나와있듯 FedPara를 사용해 설계한 VGG16과 LSTM이 모든 경우에서 더좋은 성능을 보여주는 것을 확인하실 수 있습니다. 논문에서는 결과를 통해 'FedPara가 low-rank parameterization보다 더 뛰어난 표현력과 정확도를 가지는 모델을 만들 수 있다'는 사실을 확인할 수 있다고 나와있습니다.

Communication Cost

저자는 VGG16_FedPara와 VGG16_ori를 두고 성능과 Communication Cost를 비교해봤습니다. 보통 '목적으로 하는 성능에 다다를 때까지 필요한 round'를 communication costs로 측정하는데 저자는 데이터 전송에 사용된 전체적인 bit의 크기, 다시 말해 2 × (#participants)×(model size)×(#rounds)를 communication costs로 측정하였습니다. 왜냐하면 이를 측정하는 방식이 up-/down-link를 고려하기 때문이라고 합니다. 더 실질적인 측정 기준인 것이죠.

측정에 앞서 FedPara로 만드는 VGG16의 parameter 크기를 정해야합니다. 저자는 데이터셋에 따라 모델의 크기를 각각 다르게 했는데요, CIFAR-10을 학습시킬 때는 VGG16_ori의 10.1%, CIFAR-100을 학습시킬 때는 29.4%, CINIC-10을 학습시킬 때는 21.8%의 크기를 가지는 모델로 설계했습니다.

그리고 학습시킨 후 communication costs와 성능을 축으로 하는 그래프를 그렸습니다.

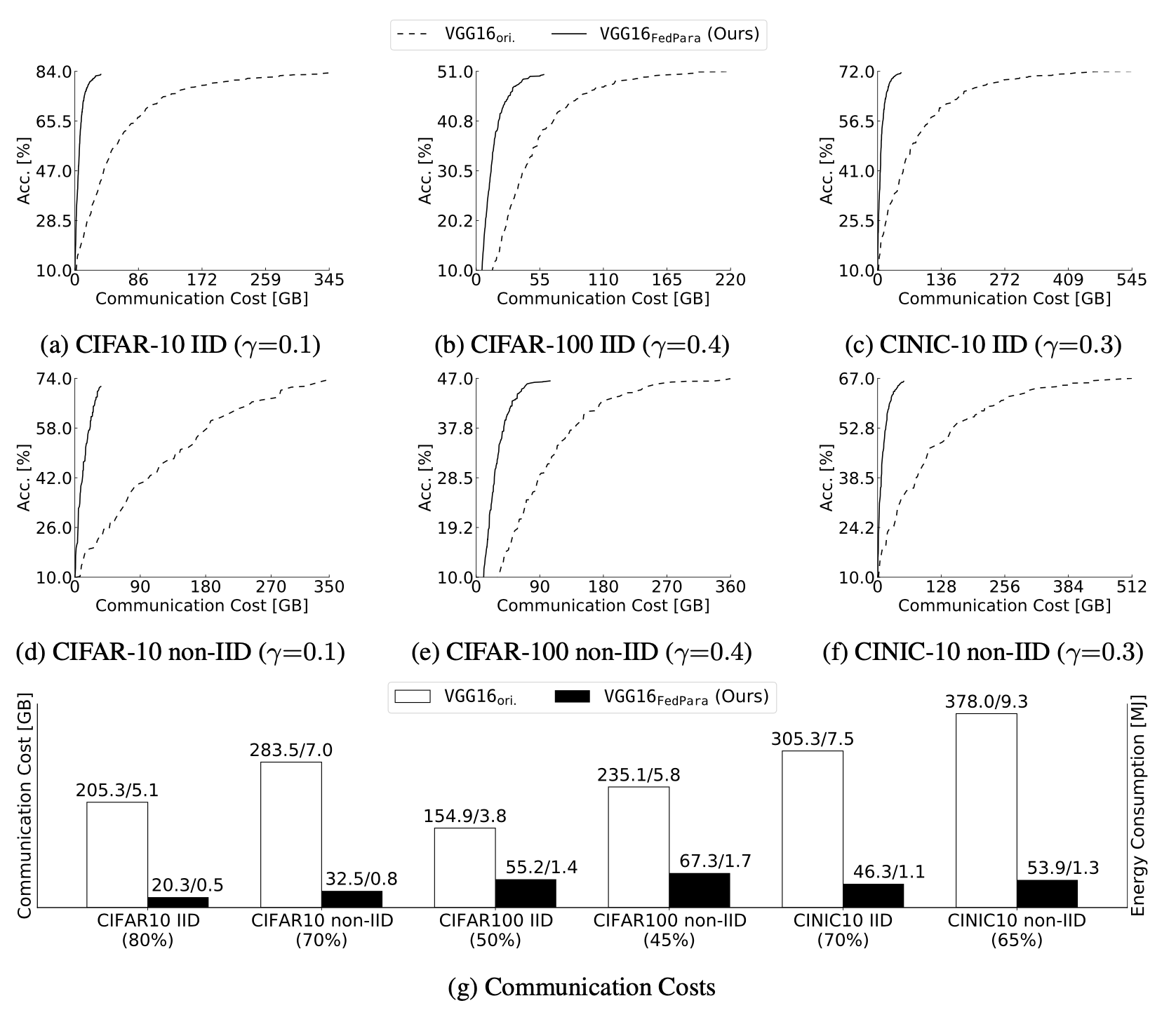
그래프가 가파르게 상승할 수록 좋습니다. 통신을 적게해도 금방 원하는 성능까지 학습되었다는 뜻이니까요. 뭐가 좋은지 알고 보니 정말 많은 차이가 난다는 것을 알 수 있습니다. FedPara가 정말 적은 통신량만 있어도 최적의 성능으로 수렴할 수 있네요. 이말은 곧 에너지를 많이 사용할 수 없는 열약한 환경에서도 금방 원하는 성능까지 학습시켜 사용할 수 있다는 뜻이니 기술의 입문 장벽이 많이 낮아질 수 있는 가능성을 보여주는게 아닌가 싶습니다.

Model Parameter Ratio

앞서 FedPara로 모델을 설계할 때 γ을 사용해 parameter 개수를 조정한다고 말씀드렸습니다. γ가 커질 수록 모델이 가지는 parameter의 수가 늘어나는 것이죠. 이말은 곧 γ를 조정해 모델의 parameter 개수를 늘림에 따라 성능이 어떻게 변하는지 확인할 수 있다는 뜻이죠. 저자는 parameter의 수에 따라 VGG_FedPara의 성능이 어떻게 달라질지 측정하였고 다음과 같은 그래프를 작성하였습니다.

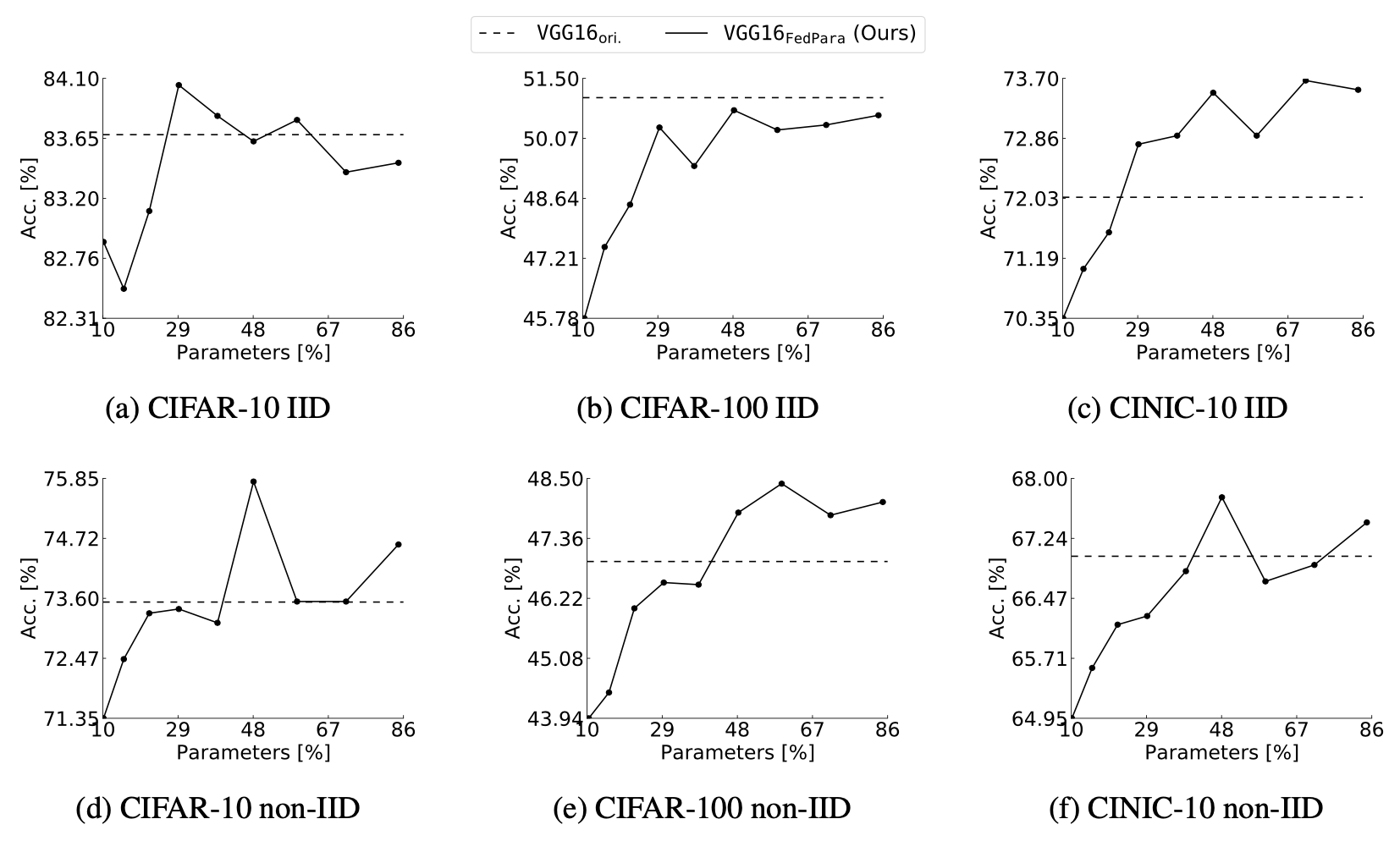
각 그래프별로 있는 node는 γ을 0.1, 0.2, ...0.9로 설정했을 때 달성한 (parameter %, Acc) 점을 의미합니다. 그래프가 조금 굴곡이 있긴 하지만 전체적으로 봤을 때 parameter의 개수가 늘어나면 성능도 증가하는 경향을 보여주는 것을 확인하실 수 있습니다. 그리고 parameter의 개수를 잘 조정하면 VGG16_ori의 성능을 뛰어넘을 수도 있다는 것도 확인하실 수 있습니다. parameter의 개수가 훨씬 적은데도 불구하고 더좋은 성능을 보여줄 수 있는 것이죠.

Compatibility

저자는 FedPara의 호환성을 보여주는 실험도 수행하였습니다. FL의 단점을 개선한 또다른 방식들과 FedPara를 같이 사용했을 때 성능을 측정하였고 'FedPara는 다른 방식과 같이 사용해도 될 정도로 호환성이 좋다'는 것을 보여주는데 성공했습니다. 성능 측정 결과는 다음과 같이 표로 나타냈습니다.

첫 번째 행은 round가 200일 때 성능을 나타낸 것이고 두 번째 행은 80%의 정확도에 도달하기 위해 필요한 round의 값입니다. IID를 만족하는 CIFAR-10을 가지고 학습을 수행하였을 때 값들인데요, 다른 방식과 같이 쓰지 않았을 때 Round = 200에서 82.88%의 정확도를 보여준 것과 비교해보면 FedAvg, FedProx을 제외한 나머지 3가지 방식과 같이 사용했을 때 성능이 더 향상되었음을 확인하실 수 있습니다. 그 중 FL에서 state-of-the-art인 FedDyn과 같이 사용했을 때 최고의 성능을 보여줬다고 합니다.

Personalization

pFedPara에 관한 실험을 설명하는 부분입니다. 이번 실험은 parameter 업데이트를 위한 기기의 sub-sampling이 없는 조건에서 수행했다고 하는데 음...그러면 모든 기기에서 학습한 global layer를 모두 사용한다는 뜻으로 추측하고 있습니다.

그리고 데이터셋은 앞서 말씀드렸듯 FEMNIST나 MNIST로 모델을 학습시키며 사용하는 기기의 수는 10대입니다. pFedPara와 함께 실험 대상이 된 방식은 Local, FedAvg, FedPer이며 여기서 Local은 각 기기에 있는 local data만 가지고 local model을 학습시킨 것을 말하며 FedAvg는 모든 parameter를 global model로 전송하는 방식입니다. local에서만 따로 저장하는 parameter가 없는 것이죠. FedPer과 pFedPara는 앞서 설명드렸으니 넘어가도록 하겠습니다.

저자는 총 3가지 시나리오에서 4가지 방식의 성능을 측정하였는데요, 시나리오는 다음과 같습니다.

시나리오 1 : FEMNIST에 있는 모든 local training data가 non-IID setting과 함께 사용됩니다. 즉, 각 기기에 있는 local model을 학습시키고 평가할 수 있는 local data가 있는 상황을 따라하는 것이죠.
시나리오 2 : FEMNIST에 있는 모든 local training data 중 20%가 non-IID setting과 함께 사용됩니다. local model을 학습시키기에는 부족한 데이터가 있는 상황을 따라한 것입니다.
시나리오 3 : MNISTdㅔ 있는 모든 local training data가 highly-skew non-IID setting과 함께 사용됩니다. 각 기기는 최대 2종류의 클래스로 구성된 데이터셋을 할당받습니다.

시나리오를 확인하며 결과를 확인해봅시다.

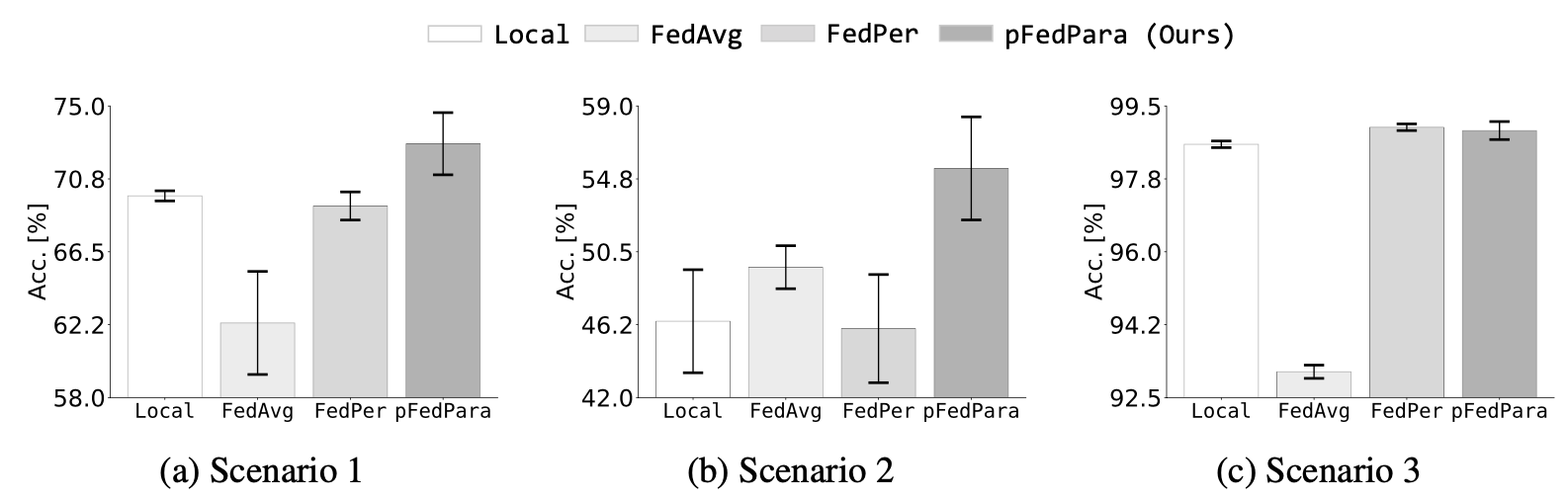
(위 그래프에 있는 error bar(I모양)는 5번의 결과 측정을 통해 얻은 95%의 신뢰 구간(confidence intervals)을 나타냅니다.)

모든 시나리오에서 pFedPara가 제일 좋은 성능을 보여주고 있습니다. 시나리오 3에서 FedPer가 근소하게 높긴하지만 error bar를 통해 pFedPara의 표준편차가 약간 더 높아 더 높은 성능이 측정될 수도 있다는 것을 확인할 수 있습니다.

이 실험값을 통해 확인할 수 있는 점은 'pFedPara는 데이터의 상황에 관계없이 가장 최선의 성능을 보여줄 수 있다'는 것입니다. 데이터가 부족한 환경인 시나리오 2에서 FedPer이 급격한 성능 하락을 보여준 것과 완전히 비교되죠. 논문에서는 이를 'pFedPara는 개인화된 모델을 global model이 저장된 서버와 각 기기가 힘을 합쳐 robustly model로 학습시킬 수 있음을 보여준다'고 말합니다.

그리고 pFedPara가 FedPer보다 communication costs도 훨씬 적습니다. FedPer은 기존 방식보다 1.07배 적은 cost가 필요하지만 pFedPara는 무려 3.4배다 적은 cost만 있어도 됩니다. 왜냐하면 pFedPara는 전체 parameter의 절반만 보내기 때문이죠. 마지막 레이어를 제외한 모든 레이어의 parameter들을 보내는 FedPer보다 훨씬 적은 parameter를 보내는 겁니다.

더 적은 통신량을 요구하지만 더 좋은 성능을 보여주는 pFedPara, 논문은 이를 'pFedPara는 Federated learning에서 개인화 성능과 통신 효율 두가지 측면에서 더욱 적합하다'고 말합니다.

Additional Experiments

저자는 앞서 말씀드린 실험들 외에도 추가적으로 실험을 수행했습니다. 그런데 논문의 양이 제한되어 supplementary에 실험 내용을 적었다고 하네요. 관심 있으신 분들은 한 번 확인해보시면 되겠습니다.

4. DISCUSSION AND CONCLUSION

FedPara를 더 발전시킬 수 있을 부분을 설명하고 결론을 말하는 장입니다.

저자는 FL에 발생하는 과도한 통신량 요구를 극복하기 위해 FedPara와 개인화를 강화시킨 pFedPara를 제안했습니다. 앞서 실험을 통해 확인하셨듯 FedPara와 pFedPara는 통신에 필요한 에너지를 대폭 줄이면서 성능은 유지하거나 오히려 더 좋아지게 만들 수 있음을 증명하였죠.

성능을 유지할 수 있었던 비결은 low-rank Hadamard product parameterization를 사용해 low-rank여도 full-rank를 만들 수 있기 때문이었습니다. low-rank Hadamard product parameterization 덕분에 이전에 제안된 low-rank parameterization 등은 도달할 수 없는 성과를 달성한 것이죠.

그리고 저자는 연구를 하면서 다음과 같은 Discussion을 하였습니다.
Discussions :FedPara는 학습 과정에서 레이어의 parameter를 만들기 위해 Hadamard product를 포함한 곱셈을 많이 수행한다. 이러한 곱셈들은 학습 중에 발생하는 그레디언트가 급격히 증가하거나 아니면 사라지거나 심지어 dead neurons가 발생할 수 있으며 임의로 초기화하는 low-rank parameterization보다 numerical에 대해 불안정할 수 있다. 우리는 실험에 사용한 parameter초기화 방식인 He 방식을 사용하는 동안은 앞서 말한 문제점을 발견하지 못했으나 우리가 사용한 모델에 적절한 parameter 초기화 방식을 조사하다보면 잠재적 불안정성이 높아질 것으로 본다.

저자는 수많은 실험을 통해 FedPara가 추가적인 cost없이 더욱 성능 좋은 모델을 만들 수 있음을 보여줬습니다. 그런데 알고보니 추가적인 cost가 없는건 아니었습니다. 학습 중에 FedPara로 만들어낸 가중치 W를 원래 방식으로 재구성을 할 때 computational cost를 추가로 요구했던 것이죠. 그래도 손해를 보는 값이 얻는 이득에 비해 미미한 수준이라 고려하지 않아도 될 정도라고 합니다.

허나 FedPara를 distributed learning에 사용했을 때 계산 시간에서 오는 손해, 다시 말해 추가적인 computational cost는 무시할 수 없는 수준이었습니다. FedPara를 사용해서 얻을 수 있는 이득이 다 묻힐 정도라고 하네요.

그래서 저자는 large-scale distributed learning에서 FedPara의 계산과 통신에 관한 효율을 향상시키는 것을 향후 연구 방향으로 고려하고 있다고 말하며 CONCLUSION을 마무리합니다.

ETHICS STATEMENT

여기서는 privacy, security, infrastructure level gap, and energy consumption 등 윤리적 측면에 대해 설명하는 부분입니다. 여기서도 유익한 정보를 많이 얻을 수 있으나 분량이 너무 많은 관계로 이 부분은 넘어가도록 하겠습니다.

---

후기

정말 오랜만에 논문 리뷰를 해봅니다. 저번주까지 개발에 모든 시간을 쏟아부어 읽은 논문들을 정리할 시간이 없었는데 이번주는 조금 널널해 이렇게 논문 리뷰를 할 수 있게 되었습니다. 오랜만에 하니 정말 오래 걸리네요. 그래도 하고나니 굉장히 뿌듯합니다.
2월이 끝나기 전에 논문 리뷰를 한번 더 하는게 목표입니다. 아자아자!
그럼 다음 글에서 뵙겠습니다.