[논문리뷰] Multi-Temporal Recurrent Neural Networks For Progressive Non-Uniform Single Image Deblurring With Incremental Temporal Training
논문 리뷰 + 구현
안녕하세요. 밍기뉴와제제입니다. 이번에 리뷰할 논문은 디노이징을 조금씩 여러번 하는 Multi-Temporal(MT) approach를 이용해 디노이징의 성능을 향상시킨 MT-RNN에 대한 논문입니다.
그러면 지금부터 논문 리뷰를 시작하도록 하겠습니다.
1. Introduction
디노이징에 딥러닝 알고리즘을 도입한 이후로 그 성능은 급격히 상승했습니다. 하나의 식으로 해결하는 기존 방식보다 계산에 필요한 시간도 급격히 줄어들었죠.
딥러닝 알고리즘으로 디노이징을 하는 방식은 크게 두가지로 나뉩니다.
- 이미지에 낀 '노이즈'를 측정
- '노이즈가 없는 원래 이미지'를 측정
이 중 성능이 더 좋은 경우는 [2. '노이즈가 없는 원래 이미지'를 측정]하는 경우입니다.
노이즈가 없는 이미지를 측정하는 방식도 크게 두가지로 나뉩니다.
- 한 번만 디노이징 (one-stage approaches)
- 여러번 디노이징 (multi-stage approaches)
당연히 여러번 디노이징 하는것이 더 좋습니다. 이 때 또다시 두가지 방식으로 나뉩니다.
- '이미지 크기'를 여러개로 만들어서 디노이징 (Multi-scale)
- 하나의 이미지를 여러번 디노이징 (Multi-Temporal)
one-stage와 Multi-scale을 그림으로 나타내면 다음과 같습니다.
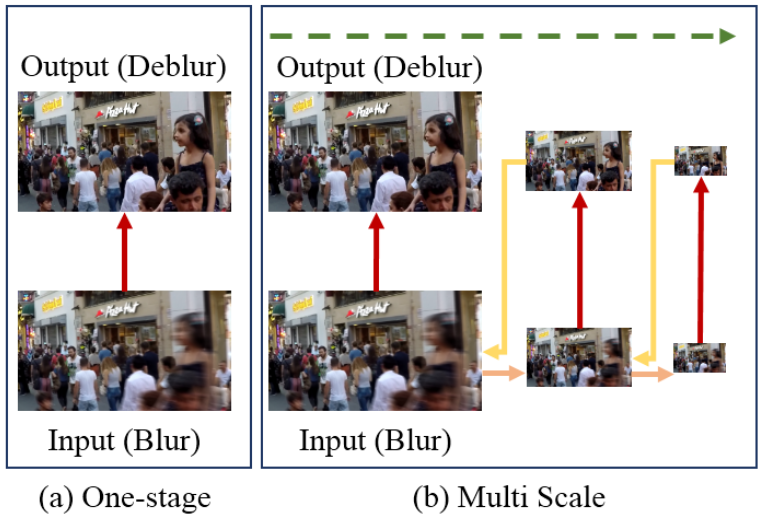
(빨간색 화살표 : model, 초록색 점선 화살표 : Multi scale, 살구색 화살표 : Down-sampling, 노란색 화살표 : Up-sampling)
이 논문이 나오기 전까지 State-of-the-art에 해당하는 방식은 Multi-scale을 이용하는 것이었습니다. 이미지의 크기를 줄여가며 디노이징을 하는 방식입니다. 이는 이미지의 크기가 줄어들면 이미지에 낀 노이즈의 크기가 줄어드는 것을 이용한 것이며 네트워크는 여러 해상도에서 디노이징을 해야하기 때문에 크기가 다양한 노이즈를 디노이징 할 수 있게 됩니다.
허나 이미지의 해상도를 줄이면 노이즈의 크기가 줄어드는만큼 선명했던 부분들이 해상도 감소로 인해 뭉개지는 현상도 발생합니다. 선명했던 부분을 되살리는 것이 디노이징에서 중요한 부분인데 이를 조금 포기한 것이죠. 다소 아쉬운 부분이 있었습니다.
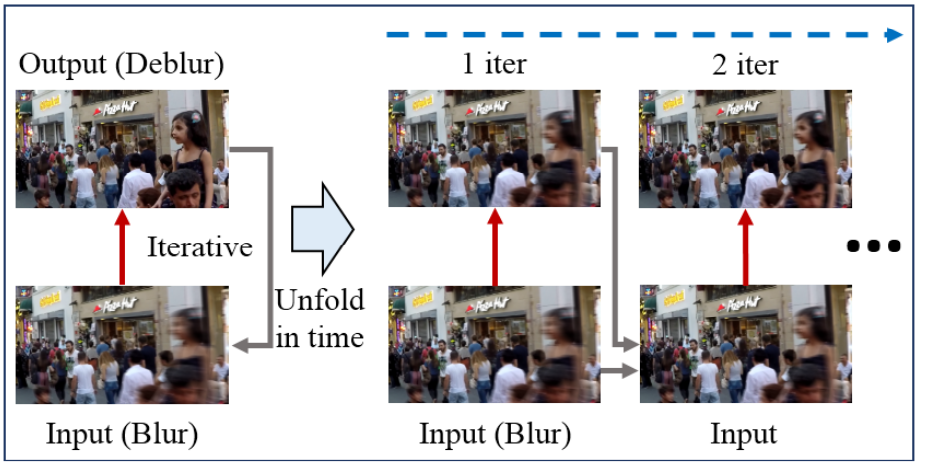
그래서, 저자는 고정된 크기의 이미지에 여러번 디노이징을 적용하는 Multi-Temporal 방식을 제안했습니다. Multi-Temporal은 '심한 노이즈를 한 번에 해결하는 것보다 약한 노이즈를 한 번에 해결하는게 더 쉽다'는 가정하에 만든 방식이며 아래 그림과 같이 노이즈를 '조금씩 여러번' 제거합니다.
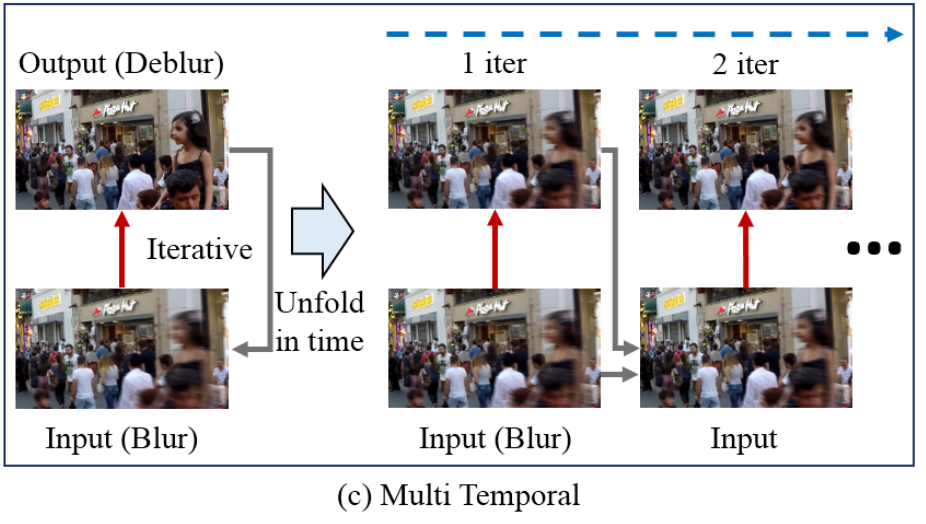
(빨간색 화살표 : model, 회색 화살표 : Skip-Connection, 파란색 점선 화살표 : Multi temporal)
Multi-Temporal은 이미지의 해상도를 줄이지 않기 때문에 이미지에 존재하는 모든 정보를 손실 없이 이용할 수 있습니다. 즉, 선명했던 부분들에 대한 정보를 잃지 않는다는 것이죠. 그래서 Multi-Temporal이 Multi-Scale보다 더 좋은 성능을 내지 않을까 추측하였습니다.
과연 저자들의 추측이 맞았을까요? 당연한 말이지만 맞았습니다.
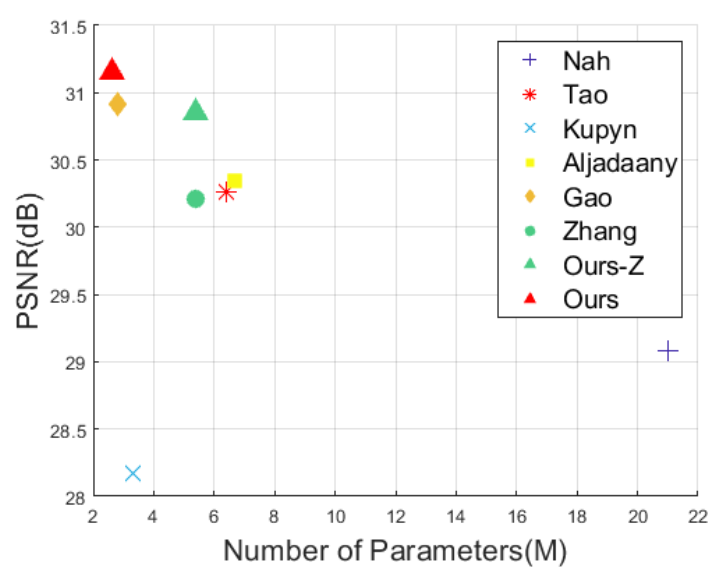
위 그림은 네트워크에 들어있는 Parameter의 개수와 성능에 대한 그래프입니다. Ours-Z와 Ours가 Multi-Temporal을 도입한 네트워크고 이 중 Ours는 저자가 설계한 MT-RNN입니다. Ours가 가장 적은 Parameter로 가장 높은 PSNR(최대 신호 대 잡음비, Peak Signal-to-noise ratio)을 기록한 것을 확인할 수 있습니다.
Ours-Zsms Zhang에 Multi-Temporal을 도입한 네트워크이며 이에 대한 자세한 설명은 Experiments에서 설명해드리겠습니다.
지금까지 디노이징의 방식과 기존에 존재했던 최선의 방식인 Multi-Scale의 단점과 이를 극복하여 더 좋은 성능의 네트워크를 만들 수 있는 Multi-Temporal에 대해 간단히 알아봤습니다. 다음 섹션 'Multi-Temporal (MT) Approach'에서 Multi-Temporal과 저자들이 어떻게 네트워크를 구성했는지 자세히 알아보도록 하겠습니다.
2. Multi-Temporal (MT) Approach
여기서는 Multi-Temporal를 구현하기 위한 데이터셋과 네트워크에 대해 설명합니다. 하나씩 살펴보겠습니다.
2.1 GoPro Dataset
우선 데이터셋부터 살펴보겠습니다. 저자는 학습하는데 사용할 데이터셋으로 GoPro 데이터셋을 사용했습니다. GoPro 데이터셋은 GoPro4 Hero Black camera(240 FPS)로 촬영한 비디오에서 얻은 프레임들로 구성된 데이터셋으로 총 15,000장이 있습니다. 이 중 22개의 비디오에 해당하는 이미지가 학습용, 11개의 비디오에 해당하는 이미지가 테스트용으로 구성되어 있습니다.
저자는 여기서 연속적으로 이어진 7~13프레임씩 묶은 뒤 평균값을 낸 이미지를 노이즈 낀 이미지(input)로, 프레임 그룹의 가운데 있는 이미지를 Ground Truth로 정했습니다.
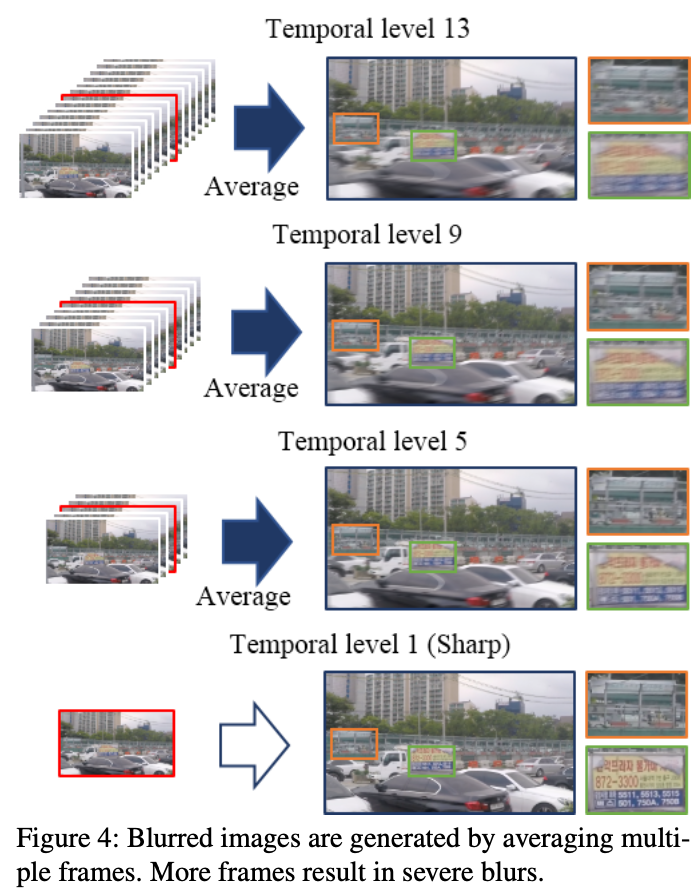
이렇게 말이죠. 여기서 TL(Temporal level) N은 'N개의 이미지로 얻은 흐릿한 이미지'를 나타냅니다. 평균내는데 사용하는 프레임이 많을 수록 더 흐릿한 프레임이 나오기 때문에 N이 클 수록 더 흐릿한 이미지가 나오는 것이죠.
2.2 Dataset For Incremental Temporal Training
앞서 TL에 대해 알아봤습니다. TL이 작을 수록 ground truth에 가까워지죠.
저자는 TL 1인 사진과 TL 7~13인 사진을 한 쌍(x, y)로 삼고 Multi Temporal 학습을 위해 데이터도 추가로 생성했습니다.
예를 들면, TL7인 이미지를 위해 TL 1-13인 이미지를 생성하는 것이죠. 왜냐하면 TL 7 이미지에서 TL 1로 디노이징 하는걸 학습시키는게 아니라 TL 7에서 TL 5, TL 5에서 TL 3, 마지막으로 TL 3에서 TL 1로 조금씩 여러번 수행하는 디노이징을 학습시킬 것이기 때문입니다.
그런데 왜 TL 9~13인 이미지도 생성하는건지는 잘 모르겠습니다.
아무튼, 이렇게 조금씩 점진적으로 디노이징 하는 'Incremental Temporal Training'을 위한 데이터셋을 생성합니다. 그럼 이 데이터셋으로 학습시킨 Multi Temporal 디노이징의 성능은 어떨까요? 다음의 표를 확인해봅시다.

위 표는 한 번 디노이징 했을 때 성능을 비교한겁니다. TL1을 예측하기 위해 TL 3~13인 이미지를 활용한 것이죠.
당연한 말이지만 TL간 거리가 멀 수록 디노이징의 성능이 떨어집니다. 왜냐하면 디노이징 해야될 양이 많기 때문입니다. 디노이징을 해야할 양이 적을 수록 성능은 상승합니다.
그렇기 때문에 저자의 '조금씩 여러번' 수행하는 Multi-Temporal은 합리적인 선택이라고 볼 수 있겠습니다.
2.3 Incremental Temporal Training
저자들이 선택한 학습 방법입니다. 앞서 2.2에서 Incremental Temporal Training를 위해 한 이미지에 대해 다양한 TL을 가진 이미지들을 생성했습니다.
이제 학습과정을 알아봅시다. 먼저 다음과 같은 반복 행동을 5~7회 수행합니다.
- 첫 번째 반복 : 흐릿한 TL 이미지(TL 13 or 11 or 9 or 7)를 입력 데이터로 랜덤하게 선택하고 비교적 선명한 이미지(TL 11 or 9 or 7 or 5)를 ground truth으로 선택한다. 입-출력간 TL차이는 2라는 것을 명심.
- 두 번째 반복 : 첫 번째 반복에서 얻은 이미지를 입력값으로 하고 그보다 더 선명한 이미지(TL 9 or 7 or 5 or 3)를 ground truth으로 선택한다.
이후 과정은 다 비슷합니다. TL 1이 출력값이 될 때까지 반복합니다.
그렇게 반복을 끝내면 TL 3을 입력값으로 하고 TL 1을 출력값으로 하는 과정을 1~3회 반복합니다. 앞서 수행한 반복의 마지막 단계를 추가로 수행하는 것이죠. 참고로 이것도 앞서 수행한 반복의 횟수에 들어갑니다.
만약 앞서 수행한 행동들의 횟수가 7이 넘어갈 경우 다시 첫 번째 반복으로 돌아갑니다. 이 때 학습을 수행한 네트워크가 디노이징을 학습할 때 사용하는 Parameter는 같으나 매번 반복할 때마다 학습은 반복횟수마다 독립적으로 수행합니다.
2.4 Progressive Deblurring With MT Approach
여기선 저자가 설계한 네트워크로 i번 디노이징한 이미지를 얻는 것을 식으로 나타냅니다.
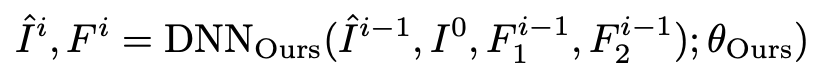
위와 같습니다. i는 반복 횟수를 말하며 I0은 네트워크에 입력값으로 넣는 이미지, I_i는 i번 디노이징을 통해 얻은 이미지, F1(i−1)와 F2_(i−1)은 i-1번 째 반복할 때 얻는 recurrent feature maps을 말합니다. 자세한 설명은 네트워크 구조를 얘기할 때 설명해드리도록 하겠습니다.
마지막으로 θ_Ours는 네트워크가 가지는 Parameter들이고 DNN_Ours는 저자들이 만든 MT-RNN을 말합니다.
2.5 Proposed MT-RNN With Feature Maps
저자들이 설계한 MT-RNN에 대해 설명하는 곳입니다. 우선 네트워크 구조는 다음과 같이 3개의 Encoder와 3개의 Decoder로 구성되어 있습니다.
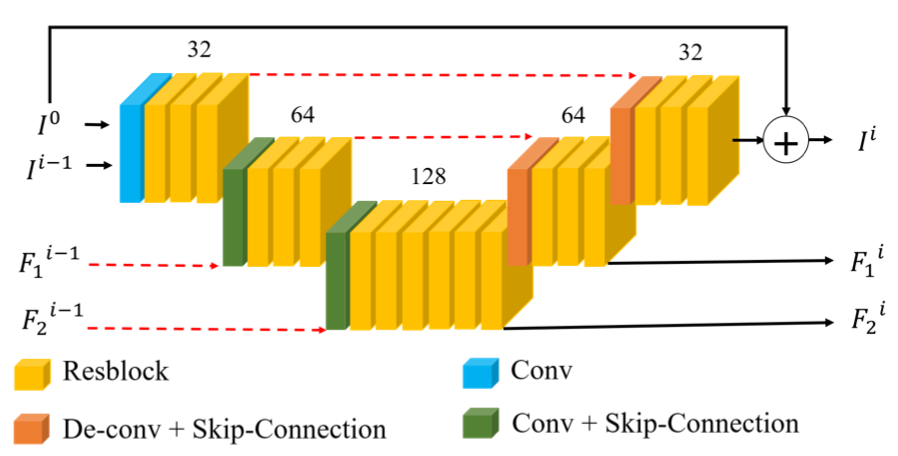
MT-RNN은 U-Net의 구조를 사용하였습니다. 먼저 Encoding 단계에서 특성맵을 추출하며 크기를 줄이고 Decoding 단계에서 특성맵을 추출하며 크기를 키우고 앞서 Encoding 단계에서 얻은 특성맵들과 결합하여 디노이징을 구현하는 것이죠.
그럼 하나씩 살펴보겠습니다.
Residual learning
MT-RNN는 특성맵을 추출할 때 residual block을 사용했습니다. ResNet에서 처음 등장한 기법이죠. ResNet의 등장 이후 특성맵 추출을 위해 ResBlock을 사용하는 네트워크가 매우 많아졌습니다.
Residual learning은 말 그대로 Residual, 남아있는 부분을 학습하는 것을 말합니다.
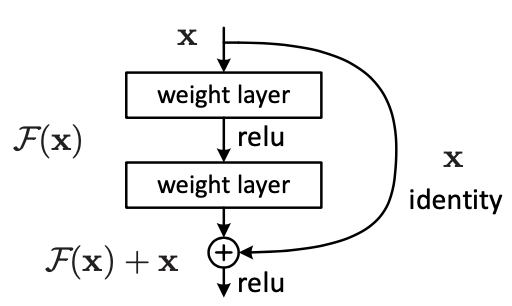
위 그림은 ResNet 논문에서 가져온 residual block입니다. 이를 MT-RNN의 경우로 생각해봅시다.
우리가 얻을 이미지는 디노이징 된 이미지 'I_deblur'이고 F(x)는 'I_residual', 입력값으로 들어가는 데이터는 'I_blur'입니다. 그러니 MT-RNN은 I_deblur = I_blur + I_residual에서 I_residual을 구현하기 위해 학습하는 것이죠.
이렇게 학습시키는 이유는 I_deblur를 학습하는 것보다 I_blur가 I_deblur가 되기위해 추가로 필요한 부분을 학습하는게 더 효율적이고 Residual learning을 적용한 네트워크들이 학습 속도도 더 빠르고 더 깊은 층을 가진 네트워크를 학습시킬 수 있기 때문입니다.
디노이징도 특성 추출을 하는 네트워크기 때문에 Residual learning이 효과가 있습니다. 논문에 의하면 입, 출력 데이터가 서로 연관성이 높기 때문에 Residual learning이 학습에 도움을 준다고 하네요.
Experiments에서 Residual learning의 성능에 관한 실험을 수행한 결과를 보여주는데 Residual learning을 이용한 네트워크가 더 높은 PSNR을 보여줬습니다.
Recurrent feature maps
MT-RNN의 구조에서 확인할 수 있듯 이전 반복에서 얻은 F1, F2가 입력값으로 넘어오고 현재 반복에서 얻은 F1, F2를 다음 반복으로 넘깁니다. 이 때 F1, F2를 'Recurrent feature maps'라고 하며 MT-RNN에서 출력한 특성맵과 F1, F2를 연결(concatenate)합니다.
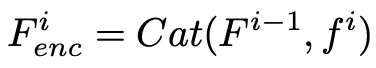
식은 위와 같습니다. f는 이전 encoder에서 얻은 특성맵이고 F는 이전 반복에서 건너온 Recurrent feature map입니다.
그리고 앞서 residual learning에서 설명하지 않았지만 입력으로 넣은 이미지를 최종적으로 추출한 특성맵과 skip connection합니다. 역시 concatenate을 수행하며 식은 다음과 같습니다.
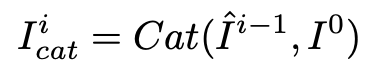
이렇게 얻은 Ii_cat = I_i과 Fi_enc를 다음 반복에서 MT-RNN의 입력값으로 사용합니다.
눈치채신 분들도 있겠지만 F1, F2은 LSTM에서 hidden state와 같은 역할을 합니다. 저자는 F1, F2에는 blur pattern이나 I_i의 intermediate results가 들어있을 것이라고 말했습니다. 디노이징을 위해 필요한 정보들이죠.
즉, Recurrent feature maps에는 I_i를 디노이징 시키기 위해 필요한 정보들이 들어있는 것입니다. I_i만 가지고 네트워크에서 특성맵을 추출하기에는 정보가 부족하니 추가적인 정보를 제공해주는 것이죠. 실제로 Recurrent feature maps을 추가했을 때 PSNR이 증가했습니다. 자세한 정보는
Experiments에서 확인하실 수 있습니다.
Loss Function
손실 함수는 L1 함수를 사용합니다. 네트워크로 디노이징한 이미지와 그에 상응하는 ground truth(TL 1-11인 이미지)를 입력값으로 받죠. 이 때 ground truth는 채널 수, 이미지 크기에 대해 정규화 처리를 수행 후 손실 함수에 넣어줍니다.
2.6 Convergence of MT-RNN over Iterations
'몇 번 반복하는게 제일 좋을까?'를 말하는 부분입니다. 저자는 TL 7~13인 이미지를 이용해 MT-RNN의 디노이징 반복 횟수에 따른 PSNR을 측정해봤으며 결과는 다음과 같이 나왔습니다.

반복 횟수가 5~6회까지 성능이 올락가다 이후 하락세를 타는걸 볼 수 있습니다. 그래서 저자는 논문을 위해 수행한 모든 실험에서 반복 횟수를 6회로 고정했죠. 그리고 모든 TL에서 Multi-Temporal이 Multi-Scale보다 좋은 성능을 보여준다는 것도 확인할 수 있습니다.
3. Experiments
논문을 쓰기위해 수행한 실험의 수행과정과 그 결과를 설명해놓은 곳입니다. 하나씩 살펴봅시다.
3.1 Dataset
저자는 GoPro dataset을 사용했습니다. 네트워크를 학습시킬 때 사용한 데이터셋이죠.
GoPro dataset은 1280 x 720 해상도를 가진 3214장의 blurred image로 구성되었고 여기서 2103장은 학습용으로, 1111장은 테스트용으로 사용했습니다. 그리고 검증, 테스트 단계에 사용할 이미지의 TL은 7,9,11,13이며 각각 개수가 균일하다고 합니다.
그리고 여기에 더해 intermediate TL image들을 추가로 생성해 학습용 이미지 5500장, 검증용 이미지 100장, 테스트용 이미지 1200장으로 구성된 새로운 데이터셋을 만들었습니다.
3.2 Implementation Details
구현에 대한 세부적인 내용입니다. 옵티마이저로 Adam을 사용했고 이에 관련된 hyper parameter들은 다음과 같습니다.
- 학습률 : 2 × 10^(−4) = 0.0002
- β1 = 0.9
- β2 = 0.999
- ε = 10−8
그리고 총 반복 횟수는 수행한 실험마다 다릅니다. 정리하면 다음과 같습니다.
Ablation Studies for Model Architecture, Studies on Temporal Steps and Parameters, Our MT Approach to Other Deblur DNNs, On Imperfect Ground Truth
논문의 Table 2,3,4,6에 해당합니다. 위 섹션에서 수행하는 실험에서 선택한 반복 횟수는 92 × 10^3 회로 46 × 10^3번 반복한 이후 학습률을 절반으로 줄이고 앞서 설명드린 새로운 데이터셋으로 학습 데이터셋을 교체합니다.
Benchmark Results
논문의 Table 5에 해당합니다. 총 반복횟수는 46 × 10^4회로 46 × 10^3번 반복할 때마다 학습률을 절반으로 줄입니다.
그리고 디노이징을 할 때 조각(patch) 단위로 수행하는데요, 조각의 단위는 256 x 256이며 데이터 증강(data augmentation)을 위해 Random crop, horizontal flip, and 90◦ rotation을 적용했습니다.
마지막으로, 실험에서 사용된 Tao의 네트워크 SRN-DeblurNet를 사용할 때 skip connection에 있던 add operation을 concatenation으로 변경해 채널의 개수가 바뀌어 1 x 1 Conv Layer를 도입해 채널 수를 조정하였다고 합니다. (Conv Layer : Convolutional layer)
3.3 Ablation Studies for Model Architecture
이제부터 본격적으로 실험 결과에 대해 설명해드리겠습니다. 먼저 Ablation Study에 대한 설명입니다. Ablation Study은 네트워크에 있던 것들을 하나씩 제거하며 제거한 것이 성능에 얼마나 영향을 미쳤나 확인해보는 활동을 말합니다. 여기서 제거되는 대상은 residual learning(R), recurrent feature map(F) 입니다. 결과는 다음과 같습니다.
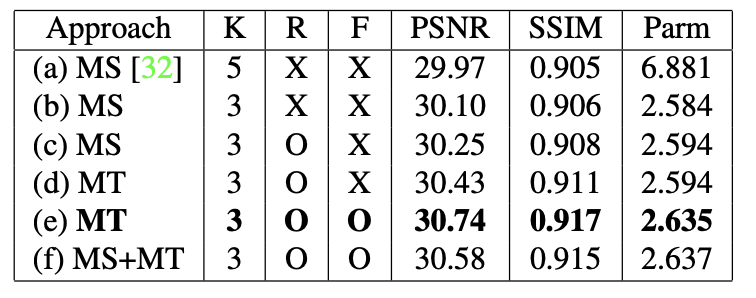
여기서 K는 CNN의 커널 사이즈, SSIM은 Structural Similarity Index Measure(구조적 유사성 수치), Parm은 네트워크의 parameter 개수이며 단위는 100만입니다.
결과표를 봅시다. 우선 커널 사이즈가 5에서 3으로 줄어들자 Parameter의 개수가 급격히 줄어들면서 성능은 상승했습니다. 커널 사이즈는 3 x 3이 좋네요.
그리고 residual learning과 recurrent feature map을 추가하니 성능이 상승했습니다. 이것들도 넣는게 좋네요.
마지막으로 앞서 확인했듯 MS보다 MT가 성능이 좋고 두 방식을 섞어서 사용하니 parameter수만 늘고 성능은 조금 하락했습니다. 섞어쓰는건 지양해야겠습니다.
3.4 Studies on Temporal Steps and Parameters
여기서는 Temporal step과 반복 횟수 등 디노이징의 횟수와 네트워크의 Parameter개수에 따른 성능을 측정한 실험의 결과가 나와있습니다.
이 중 Temporal step이 정확히 어떤 의미인지 몰랐고 지금도 정확히 알지는 못하겠습니다. 그런데 논문을 기반으로 추측해보니 TL이 줄어드는 간격을 Temporal step이라 나타낸 것이 아닌가 싶네요. 왜냐하면 논문에서 TL 간격이 클 수록 PSNR이 낮아진다는 말이 있었기 때문입니다.
그러면 결과부터 먼저 확인해보겠습니다. Temporal step과 반복 횟수, parameter에 대한 실험 결과는 다음과 같습니다.
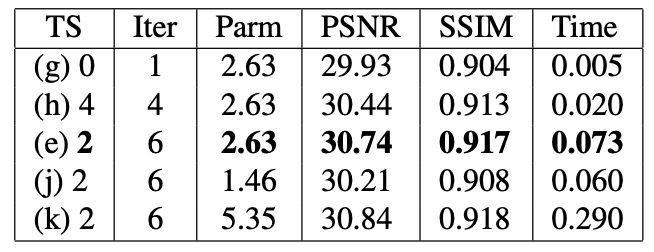
Temporal steps는 2, 반복 횟수는 6, Parameter는 263만개일 때 가장 좋은 성능을 보여주며 이 때 소요되는 연산 시간은 사진당 0.073초임을 확인할 수 있습니다.
그리고 위 표를 통해 얻을 수 있는 정보를 정리하면 다음과 같습니다.
- Temporal step이 적어야 더 높은 성능을 보여주지만 연산 시간이 늘어난다.
- Parameter 개수와 성능은 비례한다.
반복횟수 증가로 인한 성능 증가도 확인할 수 있으나 앞서 확인했기 때문에 쓰지 않았습니다.
3.5 Our MT Approach to Other Deblur DNNs
다른 디노이징 네트워크에 MT를 적용했을 때 성능 변화를 비교한 실험입니다.이번 실험에 사용한 네트워크는 Kupyn의 DeblurGAN-v2와 Zhang의 DMPHN입니다. 둘다 Multi-scale 방식을 이용해 디노이징을 수행하는 네트워크입니다.
실험 결과는 어땠을까요? Multi-Temporal을 도입하자 성능이 상승하는 걸 확인할 수 있었습니다. 결과를 정리한 표는 다음과 같습니다.
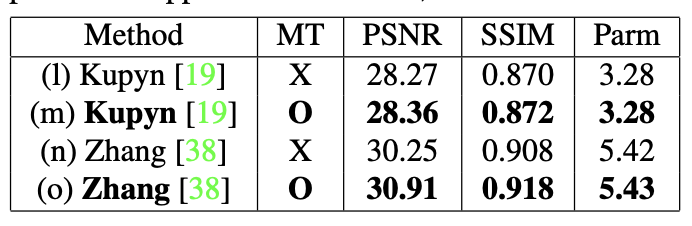
Multi-Temporal(MT)를 도입하자 성능이 상승한 것을 확인할 수 있습니다. 그런데 연산 시간이 나타나지 않은 것으로 보아 연산시간이 눈에 띌만큼 늘어난게 아닌가 추측하고 있습니다.
3.6 Benchmark Results
마지막으로 디노이징에서 높은 성능을 보여주는 네트워크와 Ours(MT-RNN), Zhang의 DMPHN에 Multi-Temporal을 적용한 Ours-Z의 성능을 측정하고 표로 정리했습니다. 표는 다음과 같습니다.
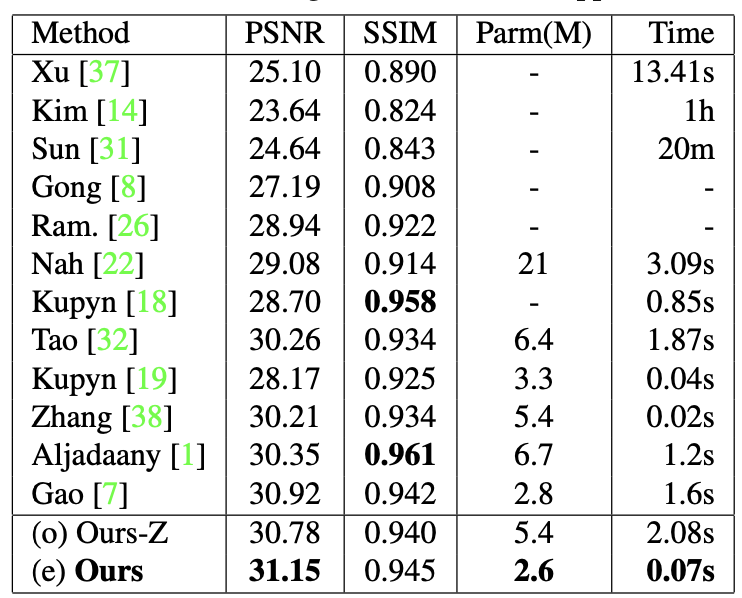
MT-RNN이 가장 낮은 실행 시간과 적은 Parameter를 가짐에도 불구하고 가장 높은 PSNR을 기록했음을 확인할 수 있습니다. SSIM은 다른 네트워크가 더 좋네요. 그래도 차이가 크게 나진 않습니다.
그리고 시각적인 결과도 논문에 나와있는데요, 다음과 같았습니다.

4. Discussion
연구 중에 나온 Discusion들이 적혀있습니다. 하나씩 확인해보겠습니다.
On Imperfect Ground Truth
GoPro 등 high speed 카메라로 촬영하는 비디오, 사진들은 객체들이 빠르게 움직인다 가정하고 찍기 때문에 약간의 노이즈가 들어있는 경우가 종종 일어납니다.
즉, '노이즈가 하나도 없는' 이미지를 얻기가 매우 힘들며 우리는 노이즈가 조금 첨가된 'Imperfect Ground Truth'를 ground truth로 사용하는 경우도 생각해야됩니다. 그래서 저자는 Imperfect Ground Truth를 사용할 때의 성능을 측정하기 위해 다음과 같이 실험환경을 준비했습니다.
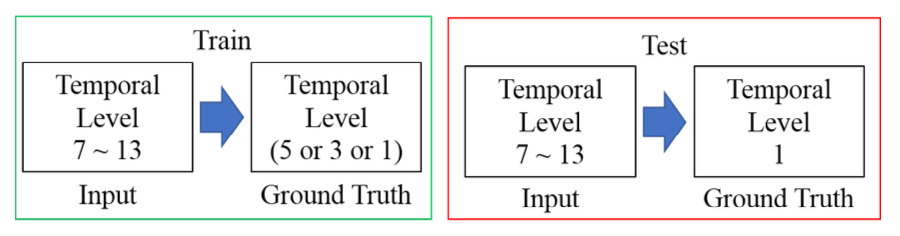
Train 단계에서 [노이즈 낀 이미지 - 노이즈가 덜 낀 이미지(imperfect ground truth)] 데이터 조합으로 디노이징을 학습시켰을 때 성능이 얼마나 될까 실험하겠다는 것이죠. 결과는 다음과 같습니다.

각각 TL이 5, 3, 1인 이미지를 Ground Truth로 정했을 때 성능을 나타낸 것입니다. 왼쪽 3개가 Multi-Temporal, 오른쪽 3개가 Multi-Scale 방식인데요, 실험에 사용한 모든 TL에서 MT가 성능이 더 좋다는 사실을 확인할 수 있습니다.
그리고 이 실험을 통해 최종적으로 "Imperfect Ground Truth을 가지고 학습시켜도 좋은 디노이징 모델을 만들 수 있다"는 사실도 확인할 수 있습니다.
Decreasing PSNR Beyond Trained Iterations
앞서 실험 'Convergence of MT-RNN over Iterations'에서 반복 횟수가 6~7회를 넘어가면 성능이 떨어지는걸 확인했습니다. 저자들은 왜 그런지 궁금해 추출되는 이미지들을 확인해봤습니다.
확인 결과, 디노이징을 하고나면 이미지의 중심 영역 근처에 작고 인위적인 어떤 것(논문에서는 tiny artifacts라고 적혀있습니다)이 생성되는데요, 반복횟수가 늘어날 수록 이 인위적인 것들이 점점 커지더다가 급격히 커졌다고 합니다. artifacts에 의해 성능이 떨어진 것이죠.
Computation Time for “Ours-Z”
'Benchmark Results'에서 Ours-Z의 이미지당 계산 시간이 2.08초나 되는 것을 확인하셨을 겁니다. MT-RNN이 0.07초인걸 생각하면 정말 긴 시간이죠. 저자는 Ours-Z의 연산시간을 0.02초로 예상했다고 합니다. 실제 연산시간과 큰 차이가 나죠. 그래서 저자는 왜 Ours-Z의 연산시간이 길어진 것인가 확인해봤고 반복 횟수별 Ours-Z의 연산시간을 측정한 결과는 다음과 같았습니다.
- 1회 : 0.015초
- 2회 : 0.092초
- 3회 : 0.581초
- 4회 : 1.073초
- 5회 : 1.568초
- 6회 : 2.065초
디노이징을 한 번 수행할 때는 0.015초로 예상한 0.02초와 큰 차이가 없습니다. 허나 반복 횟수가 증가할 수록 연산 시간이 매우 급격히 증가함을 확인할 수 있죠. 저자도 명확한 이유는 찾지 못했으며 GPU 관련 이슈로 보는 등의 추가 조사가 필요하다고 말했습니다.
Weight Sharing
MT-RNN은 디노이징을 반복해서 수행할 때 같은 네트워크를 사용합니다. 즉, 디노이징을 할 때 마다 같은 parameter(weight)를 사용하며 덕분에 필요한 parameter의 수가 줄어들었죠.
저자는 매번 디노이징을 할 때 마다 공유하는 parameter를 일부로 제한하는 'partial shared parameters'를 적용하면 성능이 더 좋아질 것이라 추측하고 있으나 이에 관련한 실험은 논문을 쓸 당시엔 수행하지 않았습니다. 그래서 나중에 이에 대한 실험을 수행하면 흥미로울 거라고 하네요.
5. Conclusion
논문의 결론입니다. 앞서 논문에서 나온 내용을 요약했으며 나중에 논문을 보실 때 읽어보시면 좋을듯 합니다.
리뷰 후기
친절한 논문이라는 생각이 들었습니다. Experiment에서 구현방식을 꽤나 자세히 설명해줘서 나중에 논문 구현할 때 좋을 논문이라 생각됩니다.
요즘 계속해서 디노이징에 관한 논문을 읽고있는데요, 디노이징 분야는 노이즈가 하나도 없는 완벽한 Ground Truth가 거의 없기 때문에 지도 학습을 적용하기가 힘든 분야라는 생각이 듭니다. 그러니까 데이터로 네트워크를 잘 학습시킬 수 있는 식, 그러니까 지도 학습에서 loss function과 같은 식의 중요성이 더 높지 않을까? 싶네요. 아직 공부가 얕기 때문에 확실한 판단을 내리기가 힘듭니다.
확실한 답을 내릴 수 있는 그날까지, 더 깊게 공부해야겠습니다.
그럼 다음 논문리뷰에서 뵙겠습니다.

한 논문에 대해 이렇게 자세히 리뷰해주신 건 처음 봤습니다. 너무 잘봤습니다!