Neural Network Model
basic building block: artificial neuron(인공 뉴런)
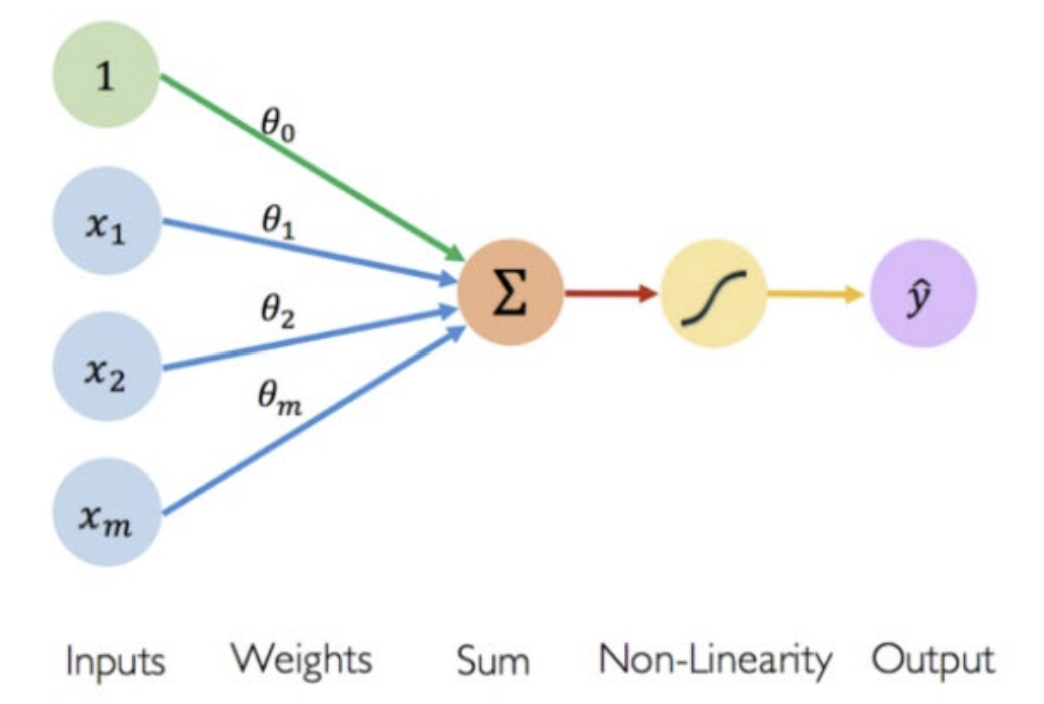
- bias : 각 뉴런에 추가되는 값 (ex. 사진에서는 1)
neural network가 학습하는 동안 weight와 함께 학습되며, activation function이 적용되기 전에 입력을 조정하는 역할을 함
Biological Neurons(생물학적 뉴런)
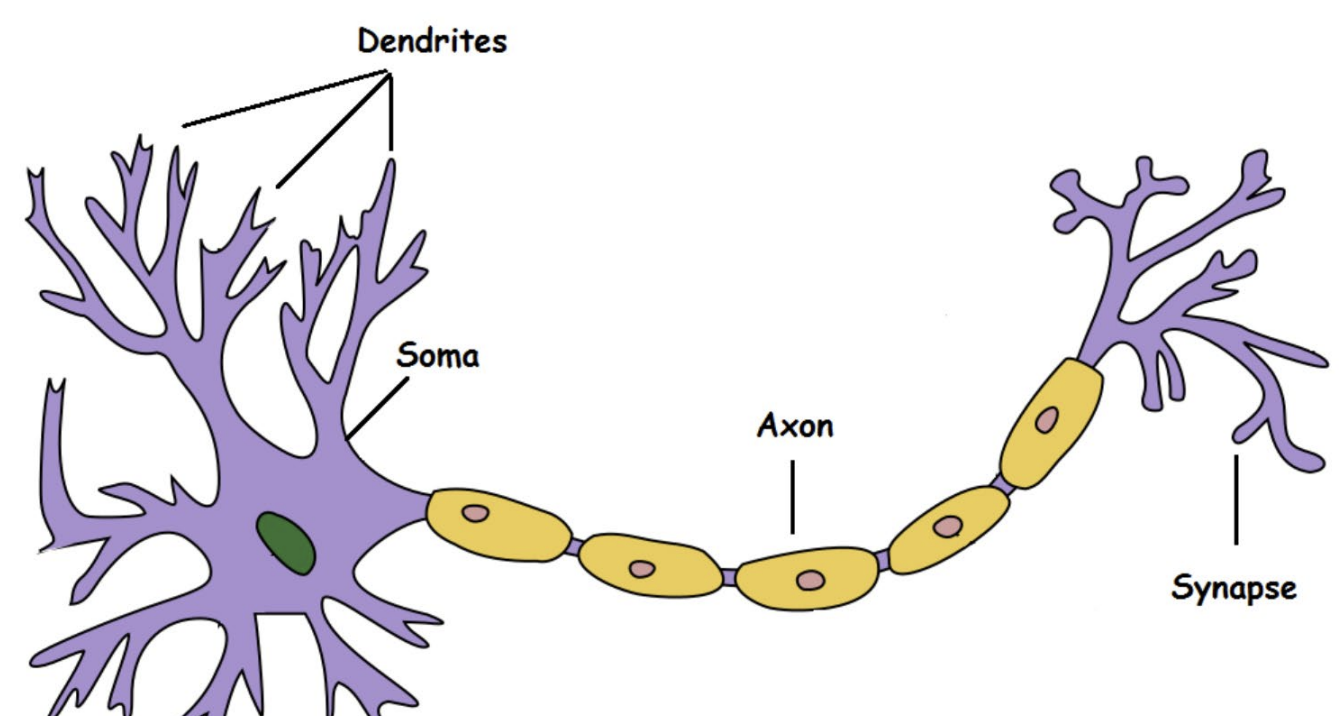
- Dendrite: 다른 뉴런으로부터 신호 수신 (input 받는 곳)
- Soma: 정보 처리 (like CPU)
- Axon: ouput 전송하는 곳 (like cable)
- Synapse: 다른 뉴런과의 연결 지점
(이후, 또다른 dendrite로 output이 들어가게 됨)
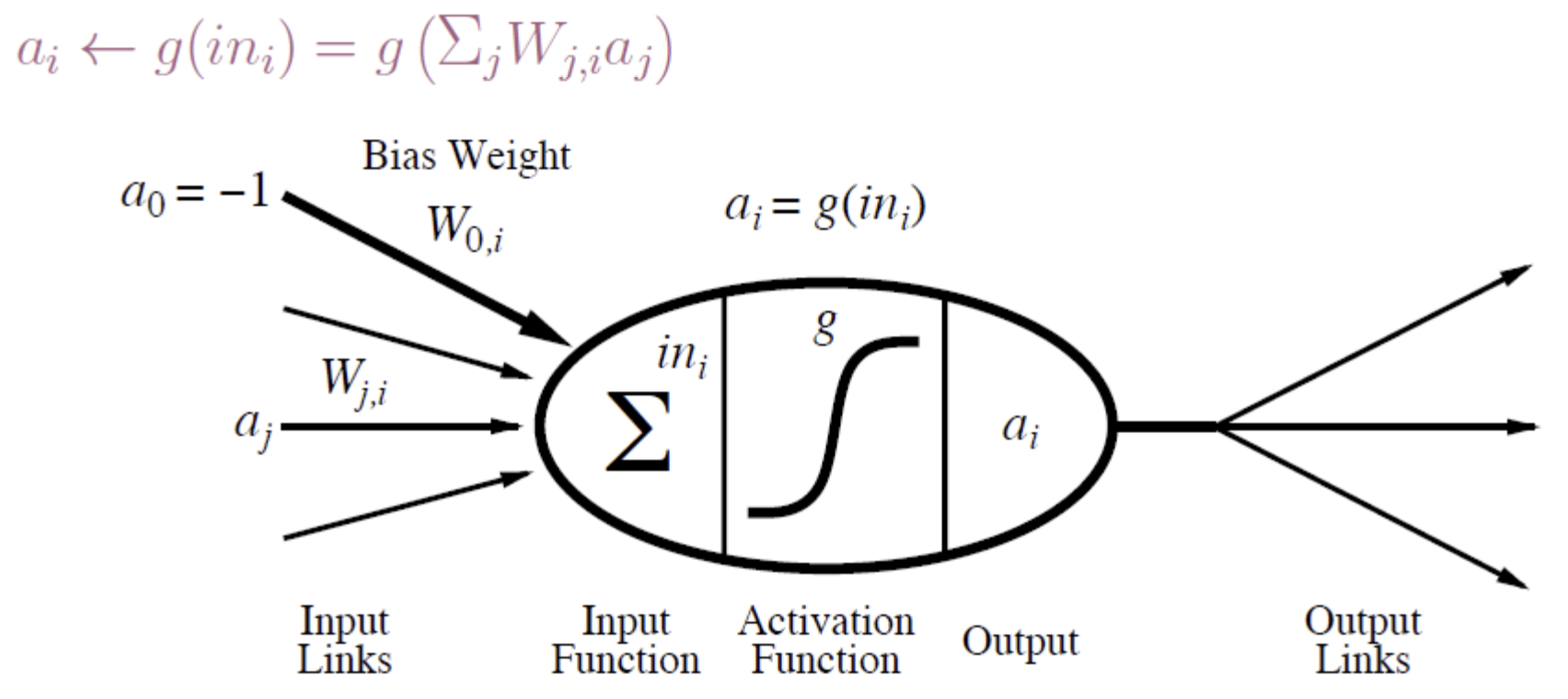
McCulloch-Pitts Neuron "unit" (수학적 모델)
- neuron의 첫 번째 계산 모델
- output == input의 "squashed"(압축된) 선형 함수
(다양한 input이 [-1,1]로 bound되기 때문)
- 과정: bias를 포함한 input들은 weight와 곱해져서 합해짐 -> 활성화 함수를 지나 [-1,1]로 output이 나옴
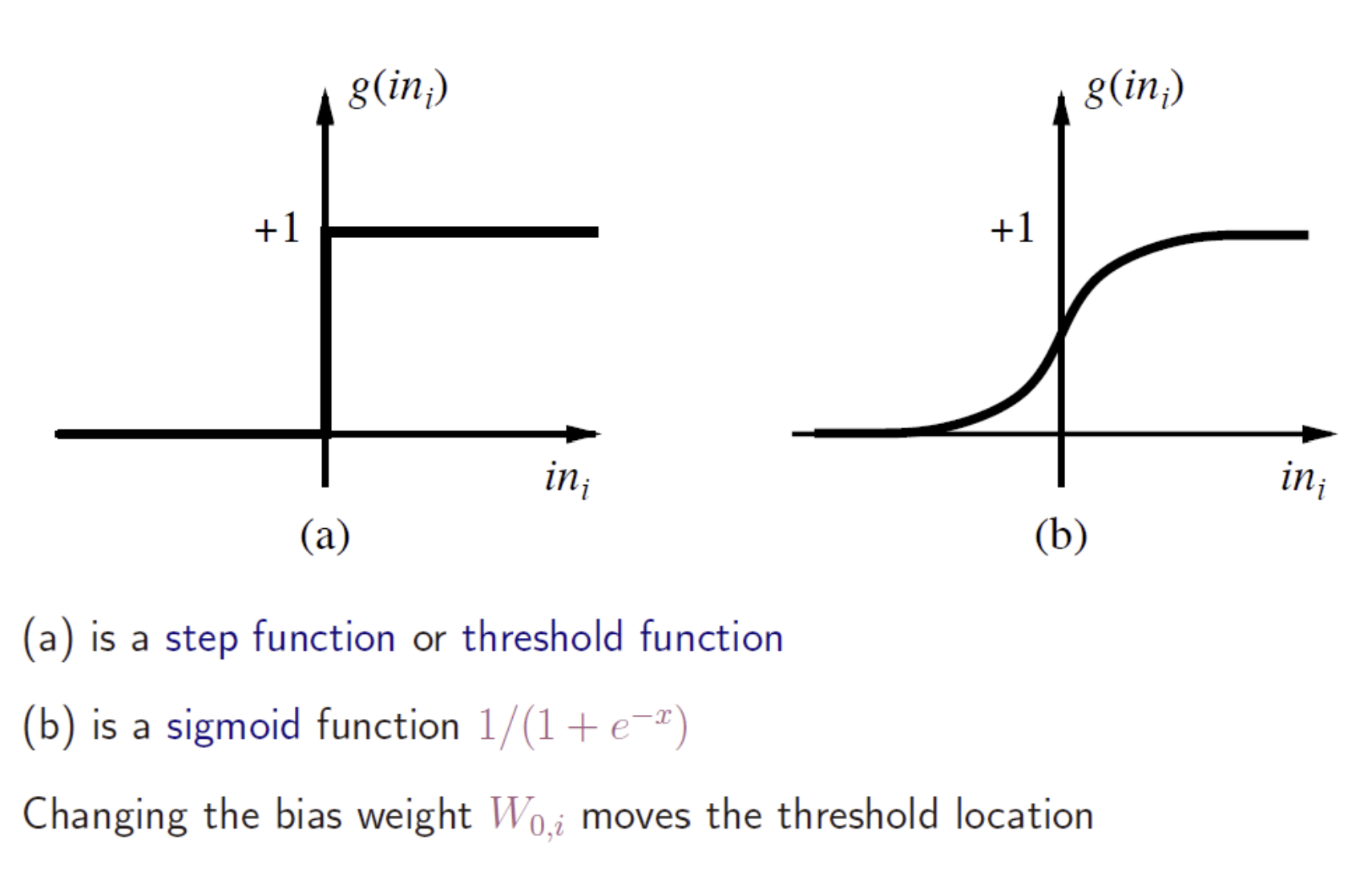
activation function
- bias의 역할: bias의 값에 따라 한 output이 도출될 확률을 높임 -> 입력을 조정하는 역할 => 즉, bias가 threshold의 위치를 이동시킴
Network Structures
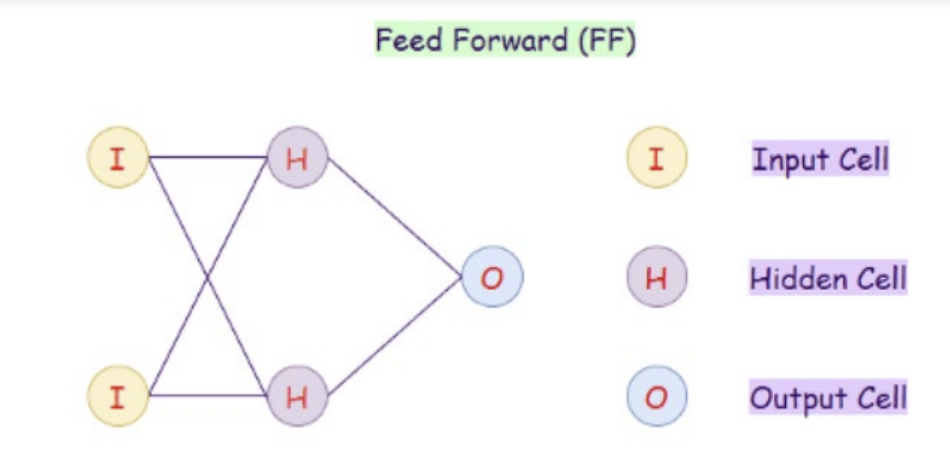
Feed-forward networks
- 단일층(single-layer) 퍼셉트론 or 다층(multi-layer) 퍼셉트론
- 함수를 구현(implement)하며 내부(internal state) X
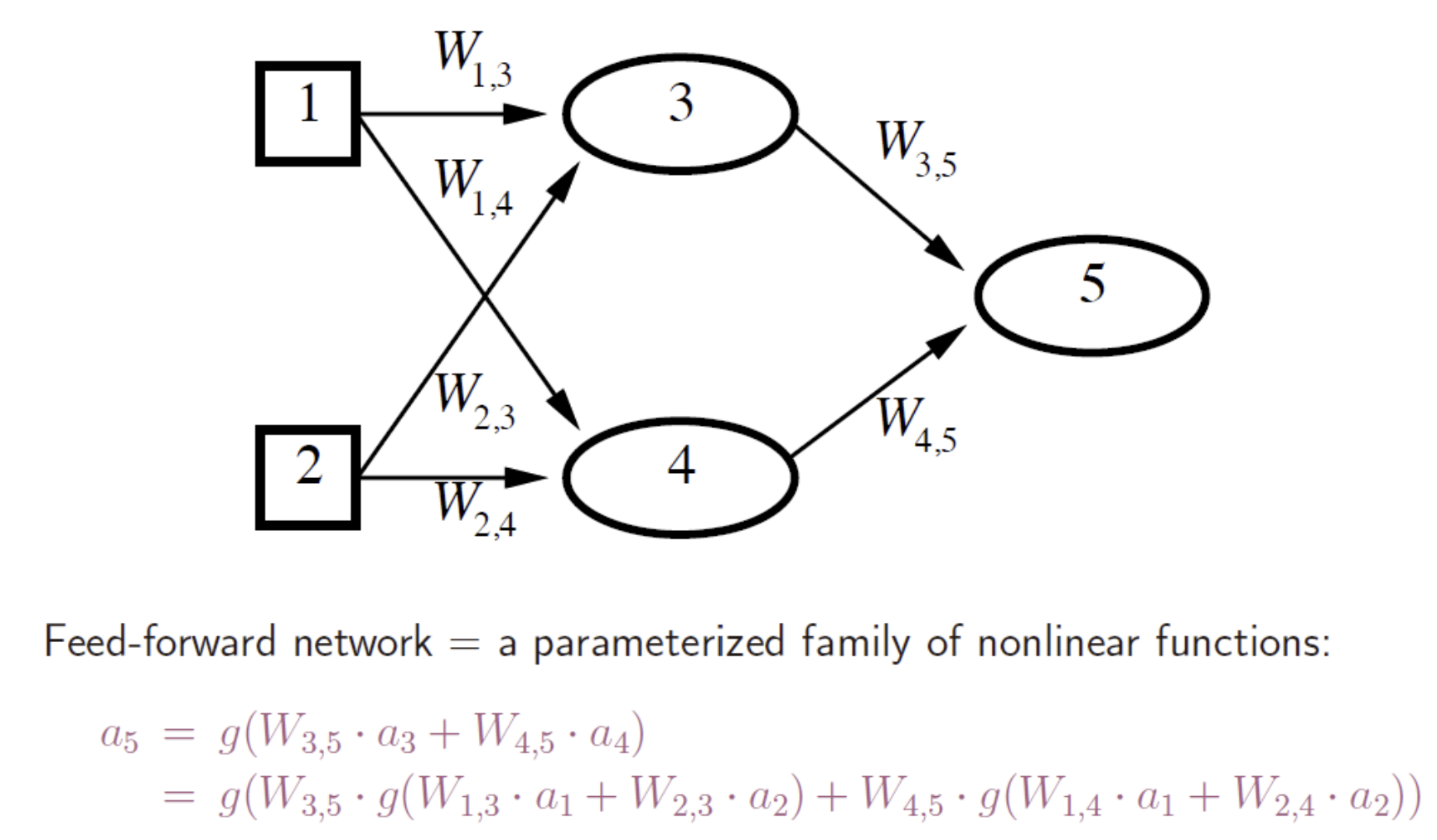
- logistic regression 함수
- notaion: a5 => act- 활성화 함수때문에 이렇게 표시, W3,5 => previous 3에서 5로 보내지는 경우
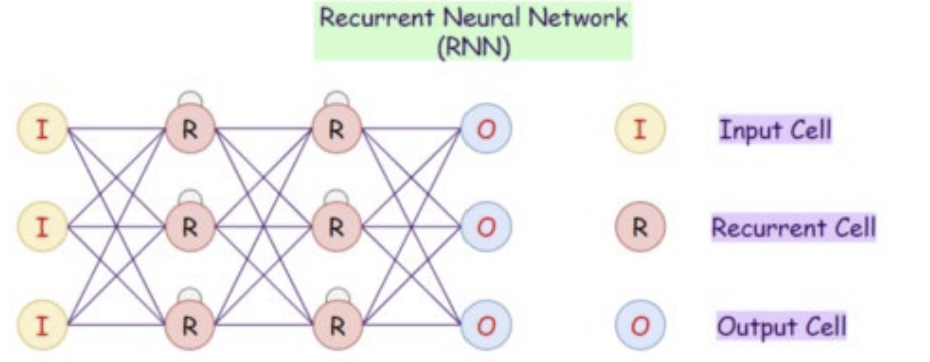
Recurrent networks
- directed cycles with delays를 가짐(자기자신에게 돌아오는 재귀적인(recursive) cycle)
- 내부 O
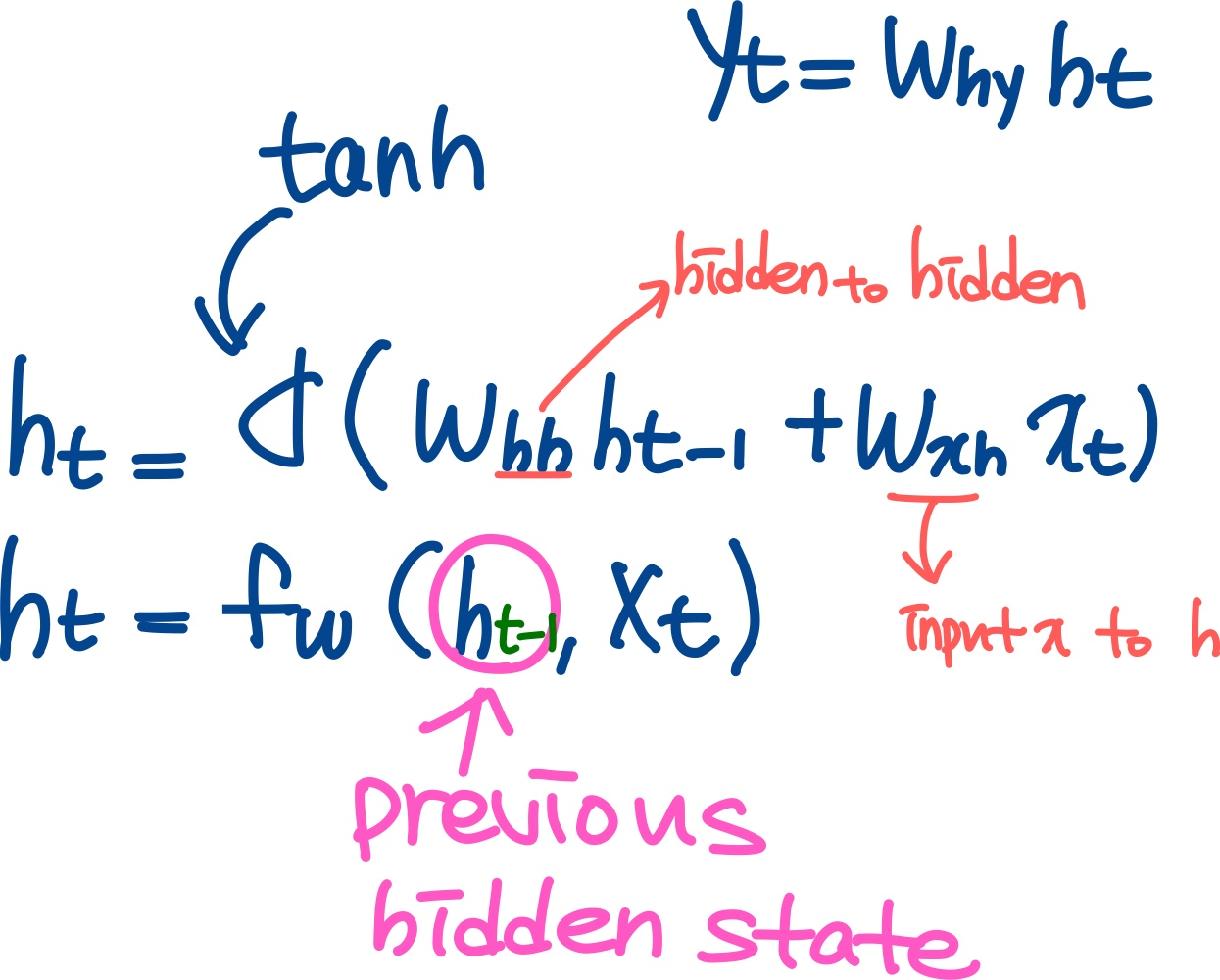
- tanh 함수
- ex. 이 문장을 이용해서 다음 문장을 해석할 때
Perceptrons
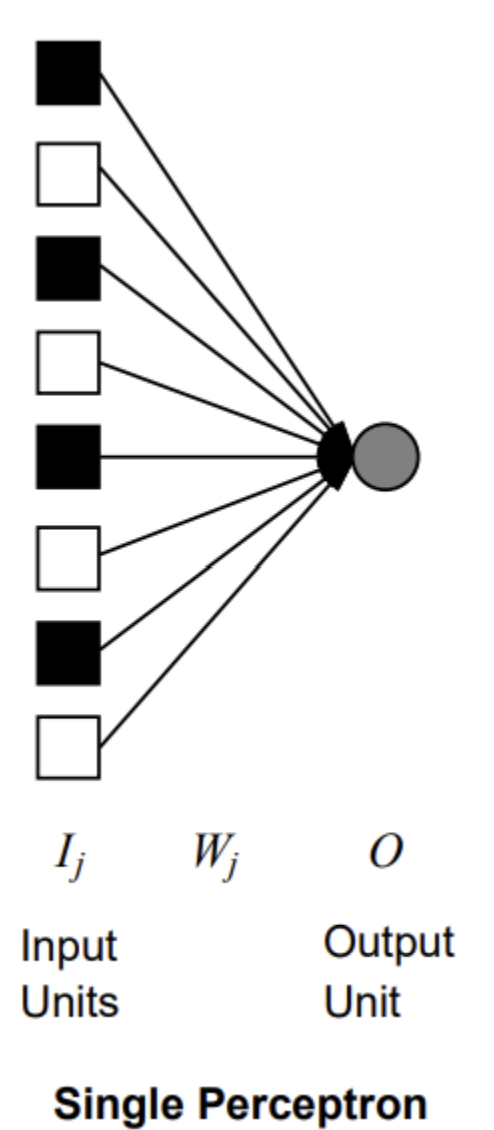
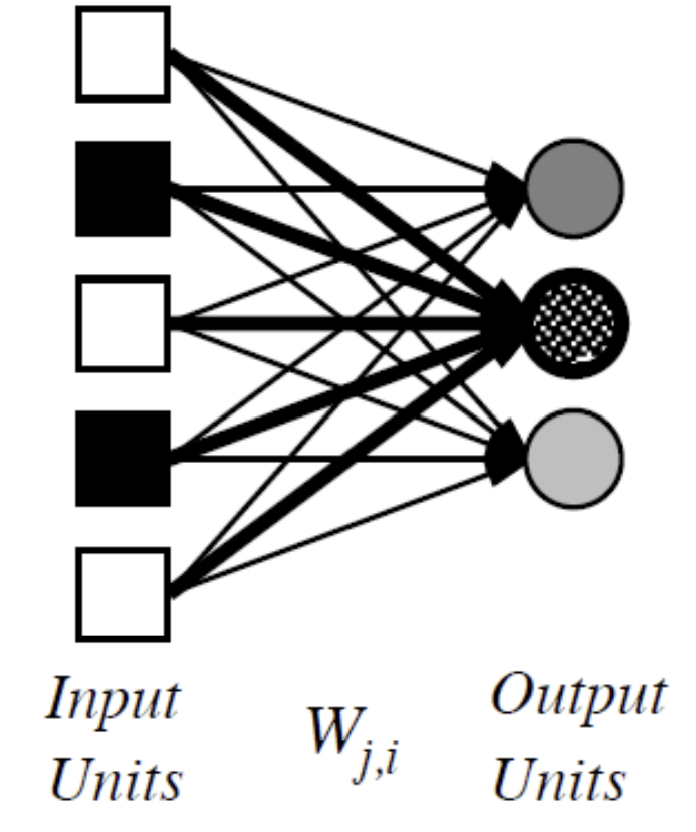
(single-layer) 퍼셉트론
- unit들이 활성화 함수로 step/sigmoid 함수를 사용함
- output unit은 모두 개별적으로(separately) 작동함 (weight 공유 없음)
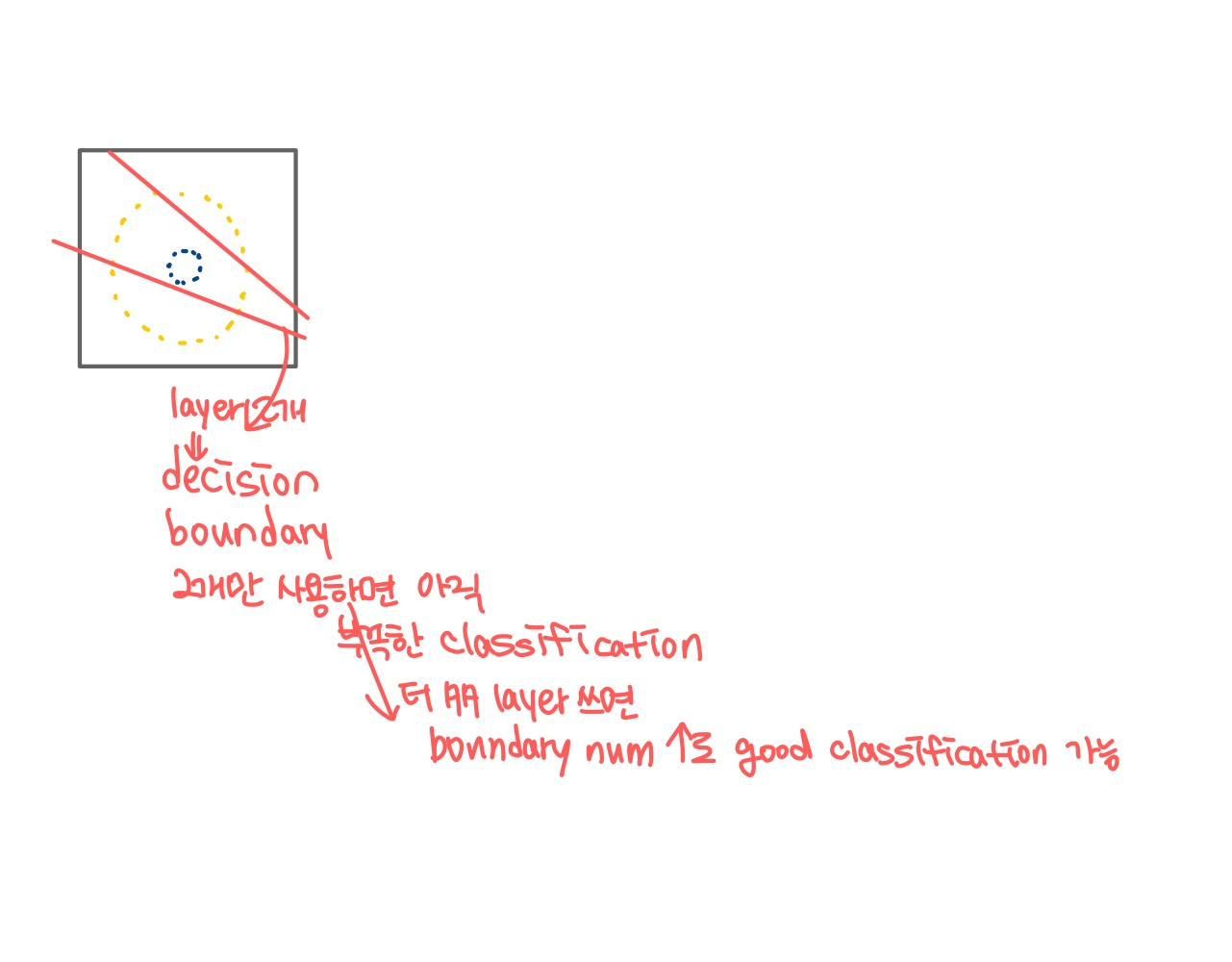
- weight를 조정하면(그림에서 두꺼운 선이 weight 大, 얇은 선이 weight 小) cliff(경계)의 위치(location), 방향(orientation), 가파름(steepness)이 모두 변화함
Perceptron learning
- 퍼셉트론이 큰 파장(stir)이었던 이유: 퍼셉트론으로 함수를 표현할 수 있다면 충분한 훈련 예제가 주어졌을 때 100% 정확하게 학습할 수 있어서
- 문제점 : 퍼셉트론은 오로지 linearly-separable 함수만 표현 가능
but, 대부분의 함수들은 비선형으로 계산된다
=> 대표적인 경우(비선형으로만 표현): XOR
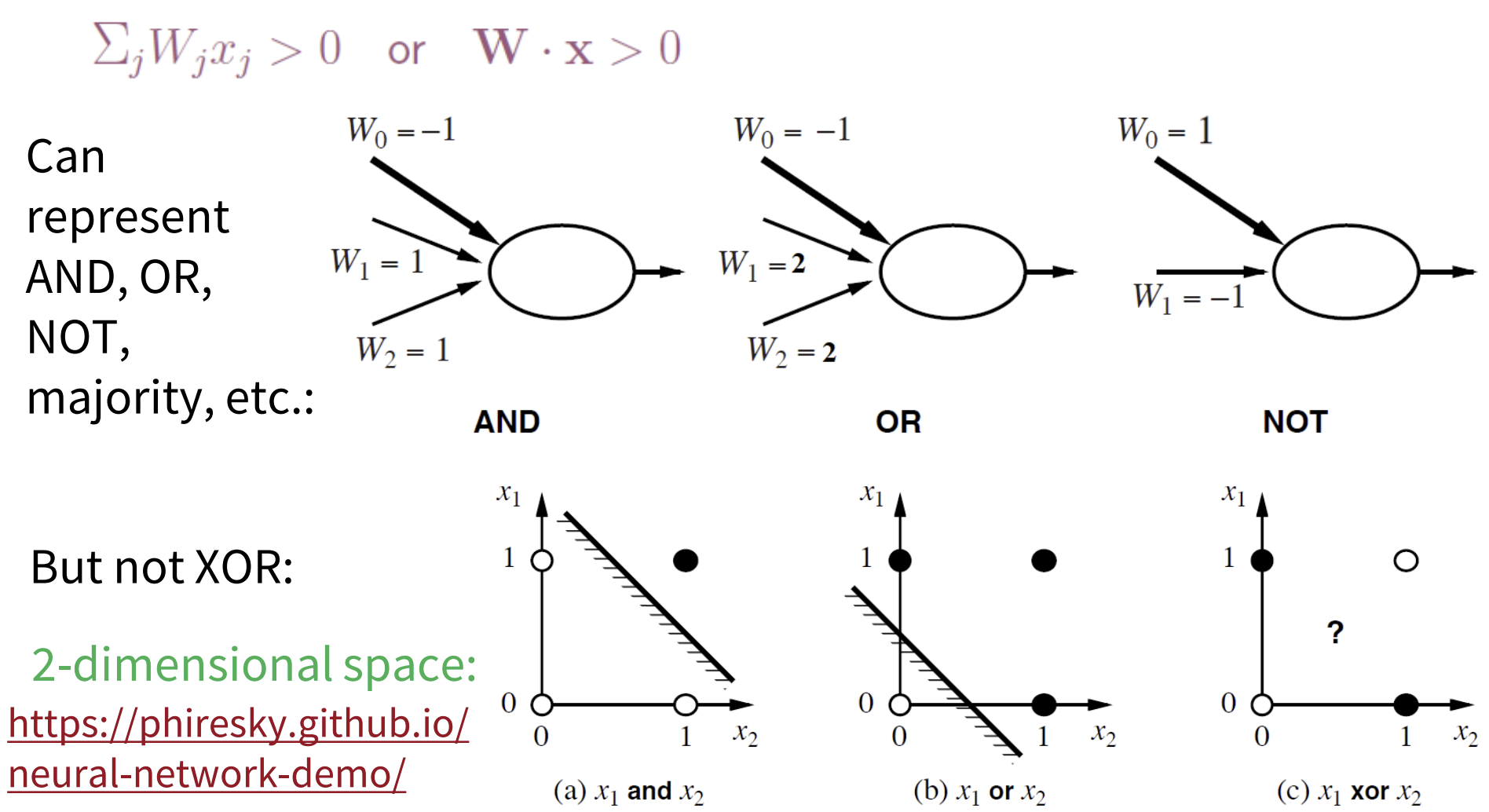
- 2-dimensional space인 경우
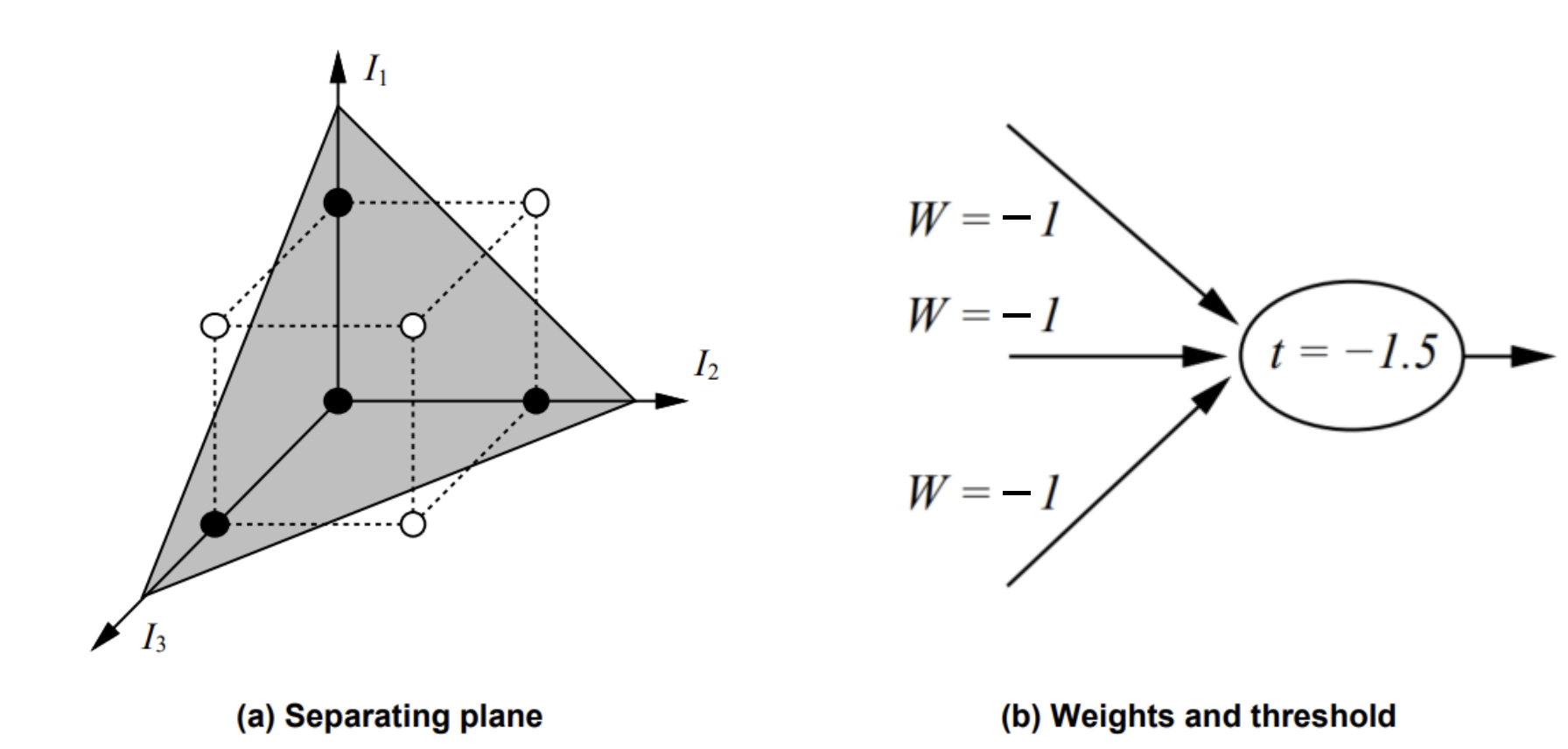
- 3-dimensional space인 경우: Minority function
- 0,1중 input에서 소수인 값을 반환하는 것
(multilayer) 퍼셉트론
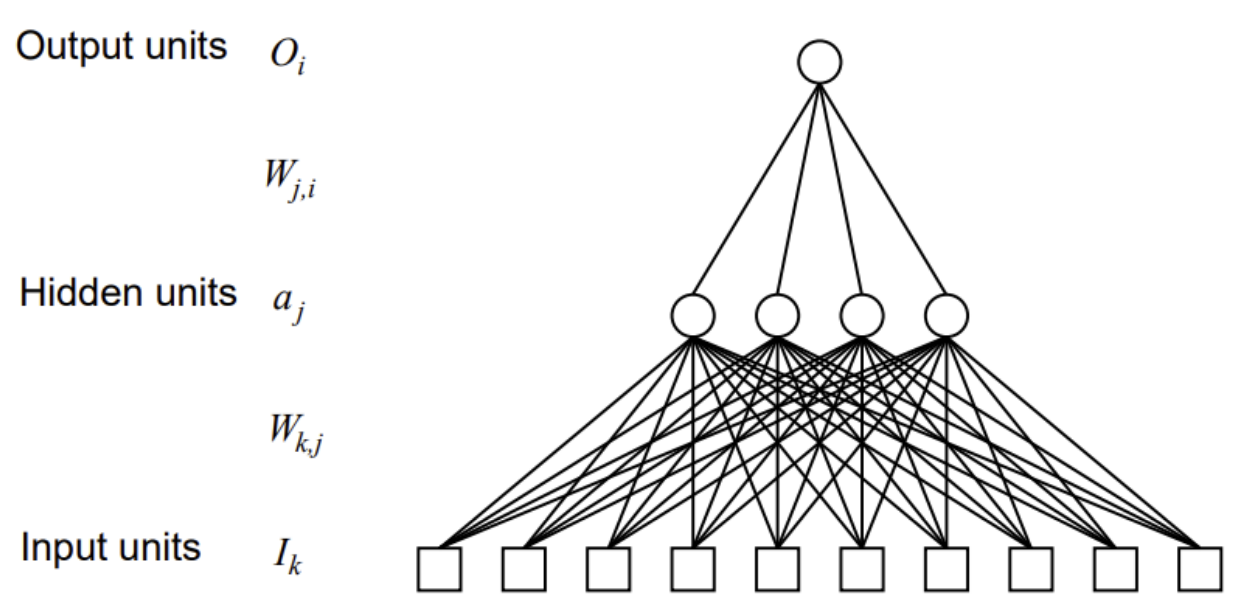
- 그래프의 root == bottom, 그래프의 leaf == top
- input unit들의 layer는 layer 수로 세지 않음 -> ex. 따라서, 사진은 hidden unit 1개/output unit 1개로 two-layer net임
- layer는 fully connected (hidden unit의 수는 수작업으로(by hand) 결정됨)
Expressiveness of MLPs (MLP의 표현력)
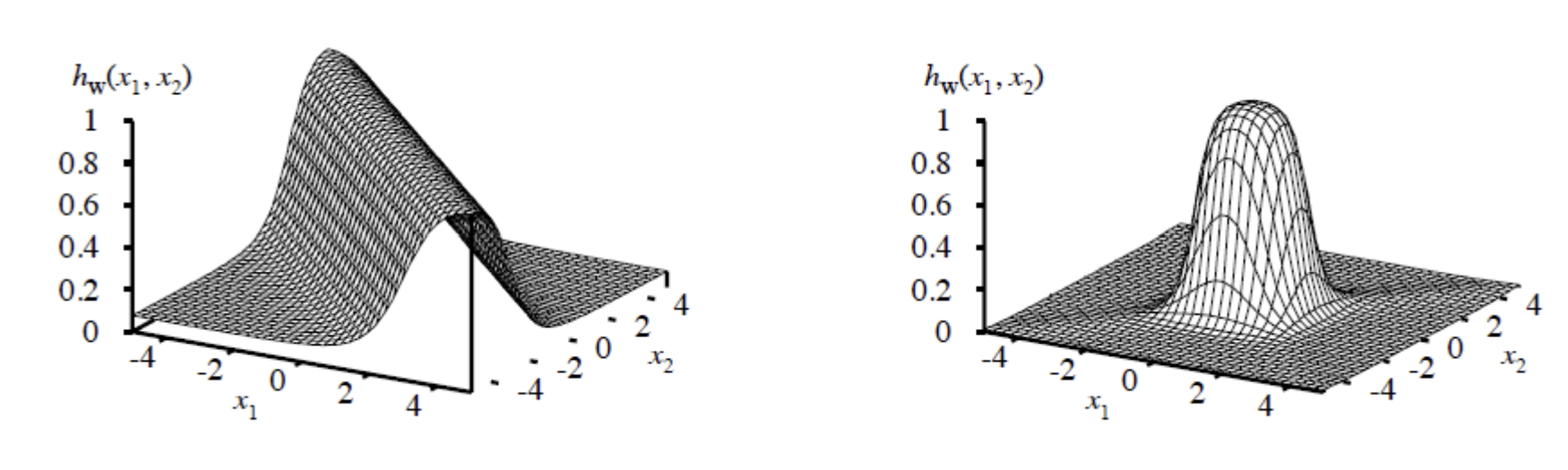
- layer가 많을수록 (==복잡할수록) 표현력이 좋은 모델을 만들 수 있음
- x1,x2 두개의 input으로 output을 나타낸 그래프
- 두 개의 반대방향 threshold 함수를 결합하여 ridge를 만든다
- 두 개의 수직인(perpendicular) ridge를 결합하여 bump를 만든다
- 다양한 크기와 위치의 bump를 더하여 어떤 표면이든 맞출 수 있다
- 증명에는 지수적으로(exponentially) 많은 hidden unit이 필요하다
Learning with NNs (수도코드)

- 새로운 data(e)가 들어와서 NN에서 나오는 output (O)
- e로부터 나온 observed output (actual measurement)
- O,T의 차이에 따라 weight를 계속해서 업데이트