Activation functions

• 기본 특징
  • (must) Non-Linear -> 비선형성
  • (must) differentiable -> 미분 가능해야함
  • zero-centered
  • bounded
    • bounded x이면, positive나 negative로 value가 폭발할 수 있음
      
  +) linear의 문제점
  신경층의 모든 layer가 선형 결합하여 아무리 깊게 layer 쌓아도 하나의 선형 함수로 변환될 수 있음 => 표현력이 제한되고 복잡한 비선형 패턴의 문제를 풀 수 없음

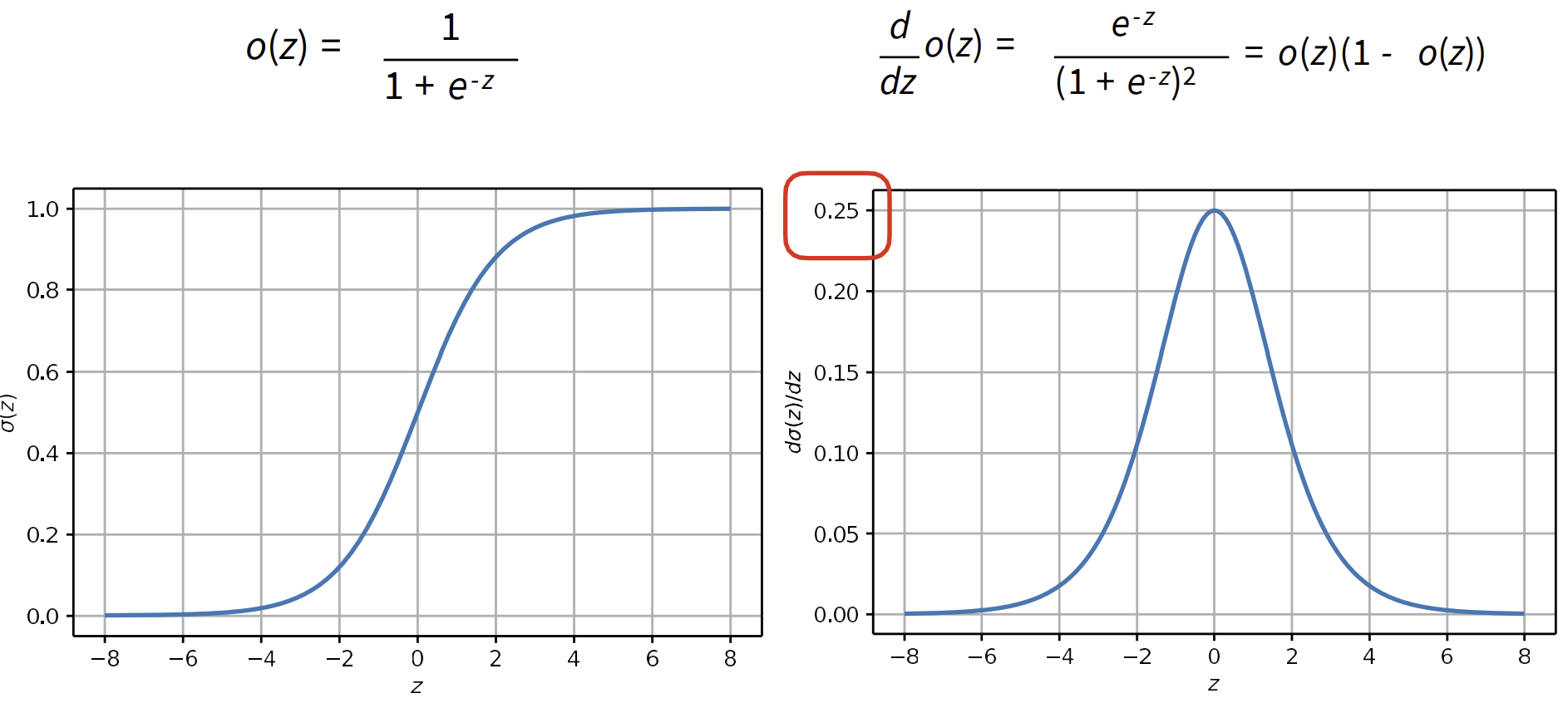
Sigmoid

왼쪽: 시그모이드 활성화 함수
오른쪽: 시그모이드 활성화 함수의 미분

• 단점(drawbacks)

  • 1. Vanishing gradients (기울기 소실)
    • saturation(포화): 출력 값이 0이나 1에 가까워져 더 이상 큰 변화를 보이지 않을 때의 상태(==출력이 일정한 값에 수렴하는 상태)
    • satureate의 성질을 보이는 x(input)이 들어오면 gradient=0(밑의 그래프)(기울기가 소실)이여서 NN이 update되지 못하는 성질이 있음
  • 2. Not zero centered
    • output이 [0,1]로 항상 positive => 0보다 작은 값 표현하지 못함
  • 3. Computationally expensive

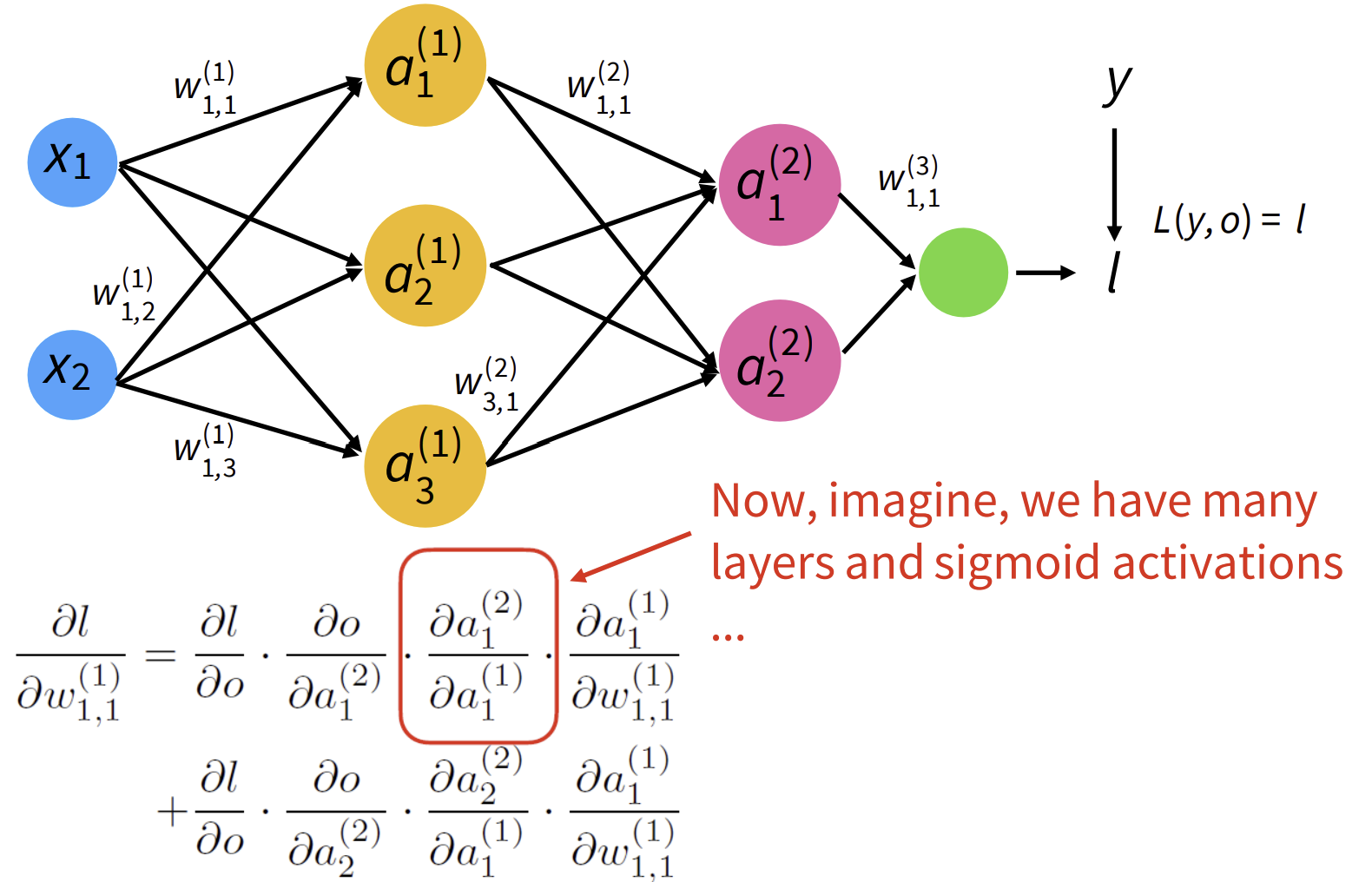
Sidenote: Vanishing/Exploding Gradient Problems

• 실제 output, NN의 output(==l)-> L(y,o)=Loss(label,model의 output)
  - Loss: label과 model에서 나오는 output의 diffrence 계산

이러한 model의 loss를 미분한 식: chain rule를 기반으로 분리
-> activation function을 미분한 것들이 계속해서 곱해지게 됨

• 시그모이드 함수의 미분한 함수의 maximum(==largest gradient)은 0.25
• 따라서, chain rule에 따라 actuvation function의 미분한 값들이 계속 곱해지게 되면 0에 가까워져 다른 gradient도 degrade(저하)시킴!!

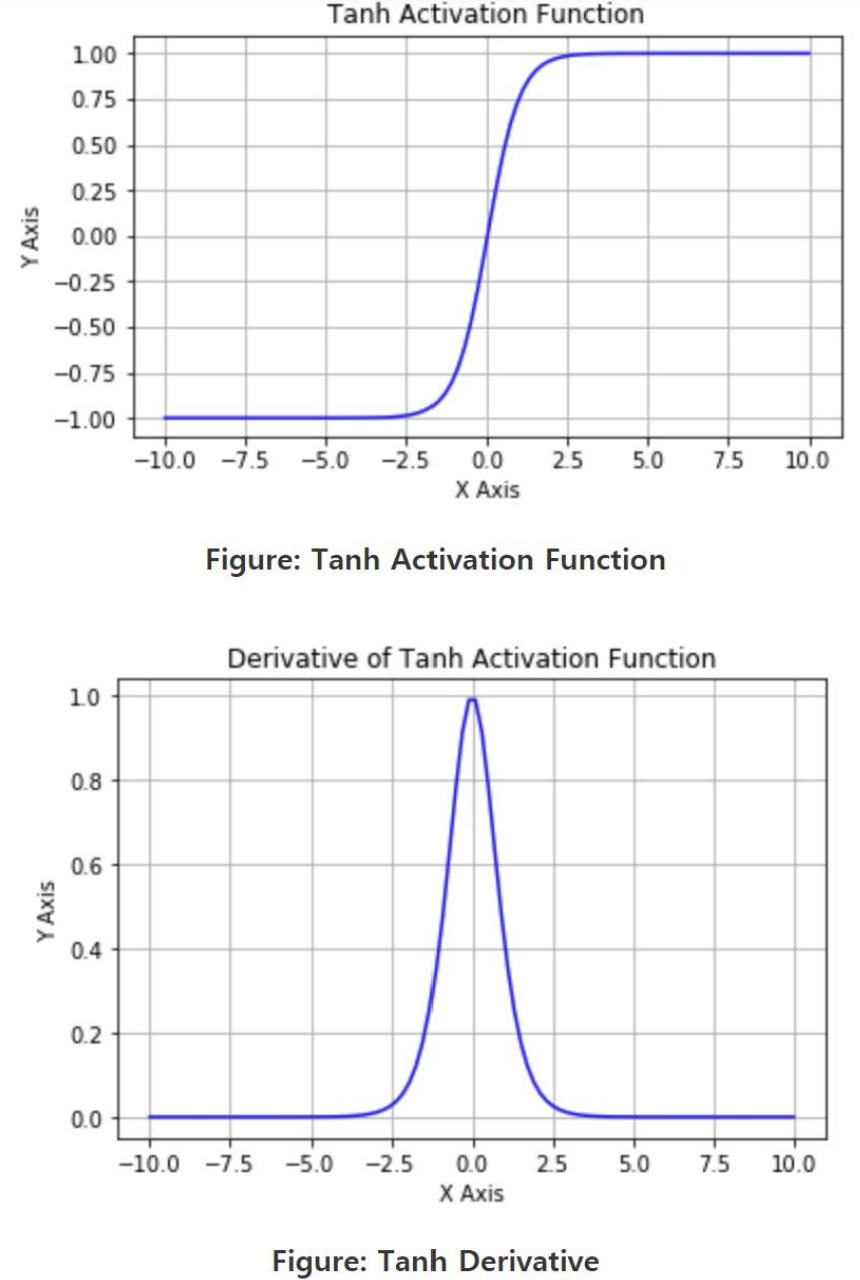
Tanh

왼쪽: 하이퍼볼릭 탄젠트 활성화 함수
오른쪽: 하이퍼볼릭 탄젠트 활성화 함수의 미분

• 장점
  • 1. zero-centered
    • [-1,1]
  • 2. squashed(압축)
    • 1과 1 사이에서 출력이 압축된(squashed) 상태
• 단점
  • 1. vanishing gradient problem
    • saturate되는 부분에서 gradient가 kill됨

+) 특징: 입력 값이 중간 범위에 있을 때 비선형적으로 변함(비선형성)

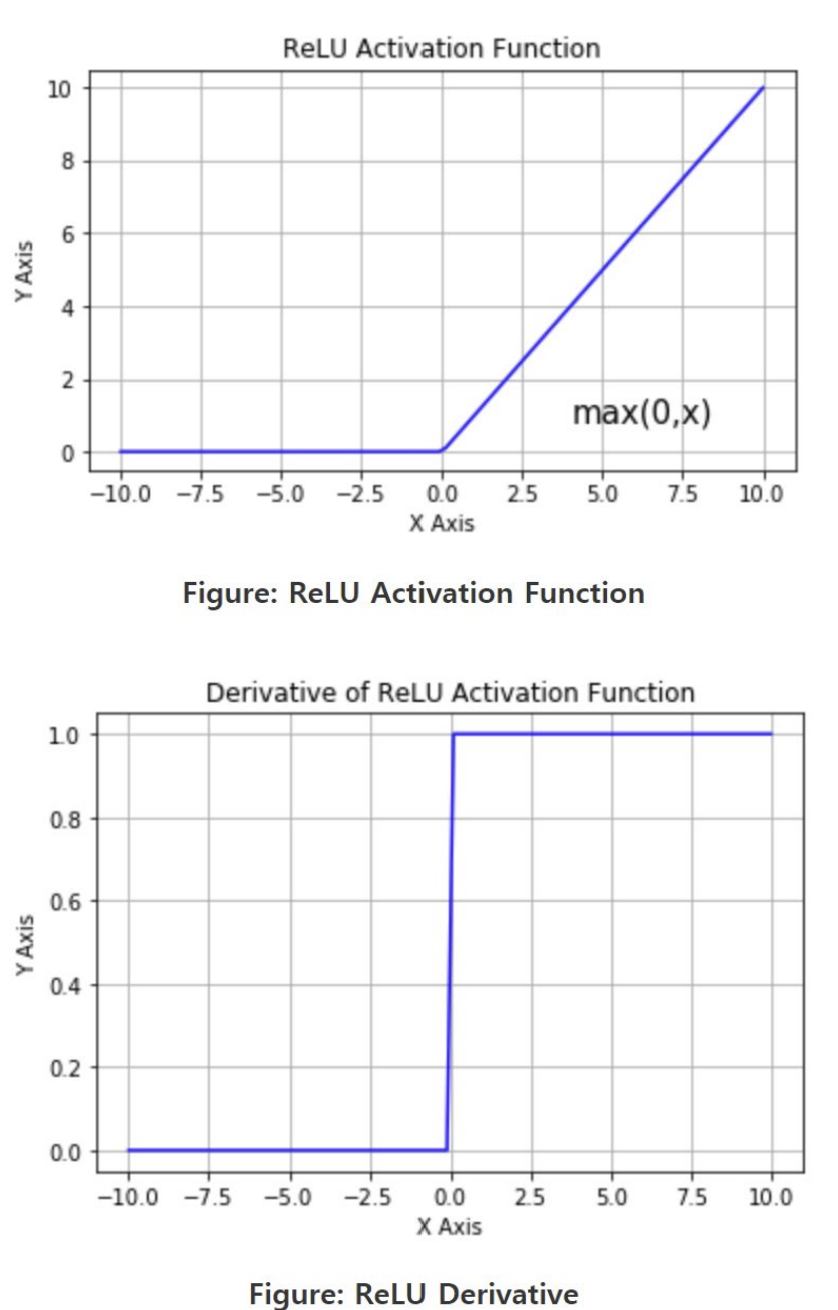
Rectified Linear Unit (ReLU)

왼쪽: ReLU 활성화 함수
오른쪽: ReLU 활성화 함수의 미분

• 장점
  • x(input)이 positive일 때 linear line이고 x(input)이 negative일 때 0이므로 계산 쉬움
• 단점
  • Not zero-centered
  • x<0 일때만 Vanishing gradient issue
    • x가 0보다 클 때는 미분값이 1로 기울기 소실이 일어나지 않음

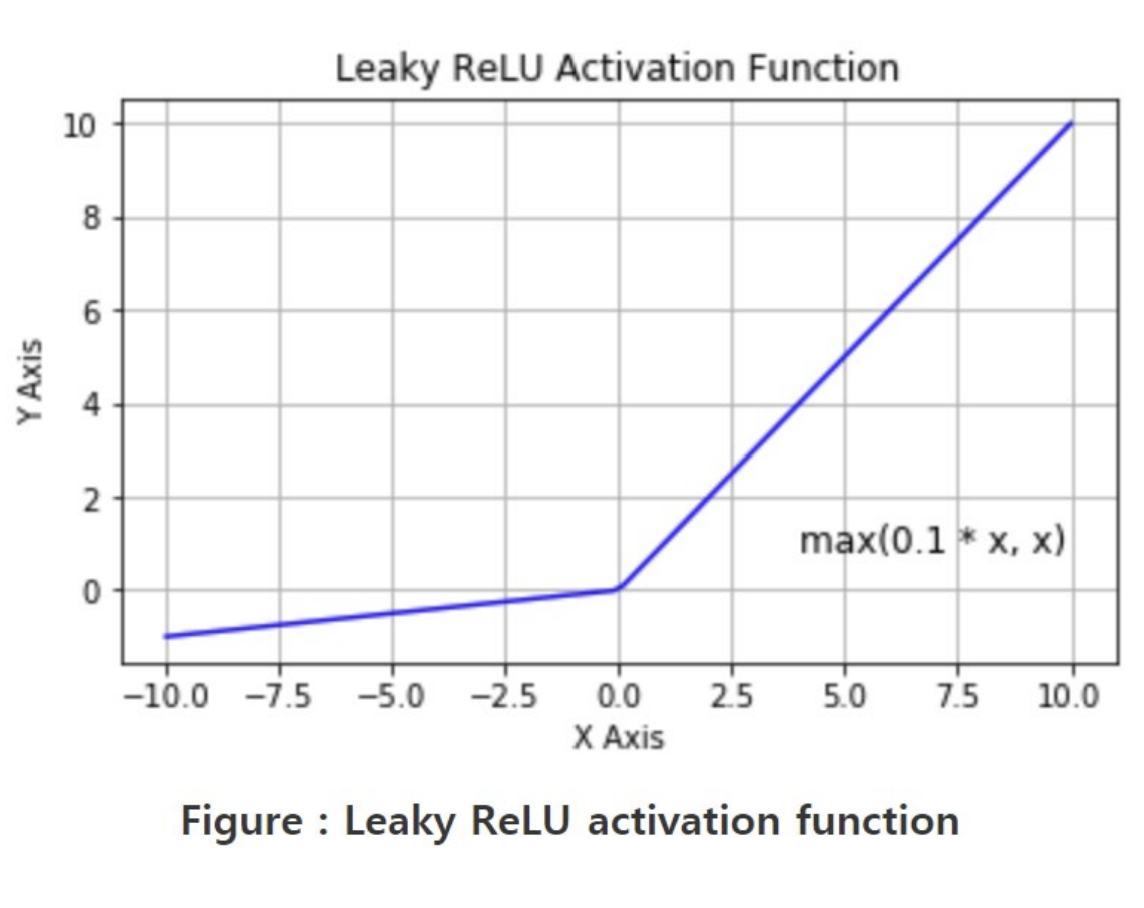
Leaky ReLU

• ReLU의 두 번째 단점을 없앰!
  • x<0일 때 작은 positive slpoe(0.1)을 더하여 negative 영역을 완전히 죽이지 않음

Building a Neural Net

1. if input layer의 수가 hidden layer의 수보다 많을 때
   • 중요한 input의 정보들이 hidden layer로 encoded(정보가 특정 형식으로 변환하거나 압축)되는 효과
2. if input layer의 수가 hidden layer의 수보다 적을 때
   • input에 대한 더 다양한 feature를 생성하여 모델의 표현력을 높이는 효과
   • but, overfitting 문제가 생길 수 있음

=> hidden layer의 optimal size는 input과 output size를 바탕으로 결정해야됨 (여러 경험과 error를 바탕으로 실험해봐야함... 즉, 현재 단계에서 감자girl은 더 공부에 매진하는 수밖에 없음)

-> 2006년 이후 HW(CPU), SW(batch norm-배치 정규화,ReLU)의 발전으로 깊은 layer를 train하기에 용이해짐 (== 하나의 hidden layer로도 깊은 network를 train할 수 있게 됨)

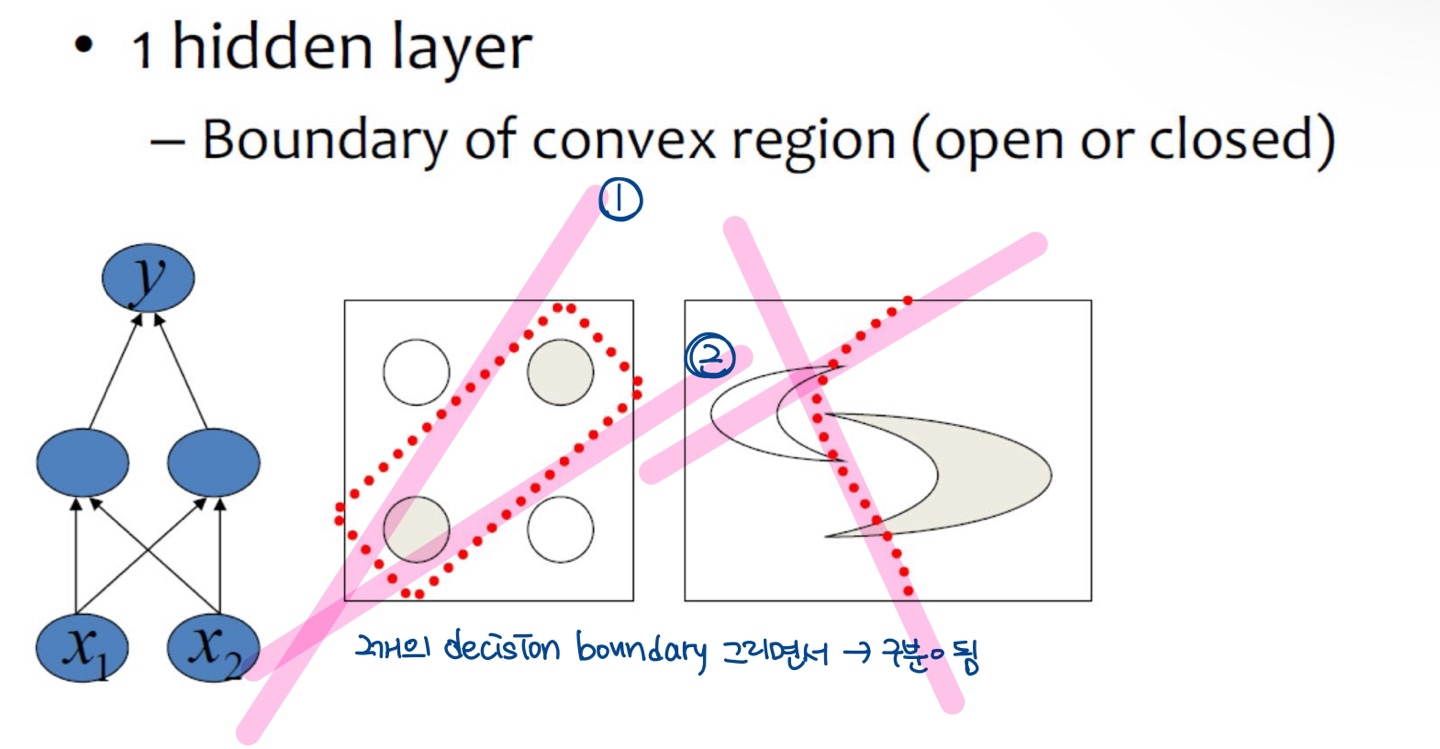
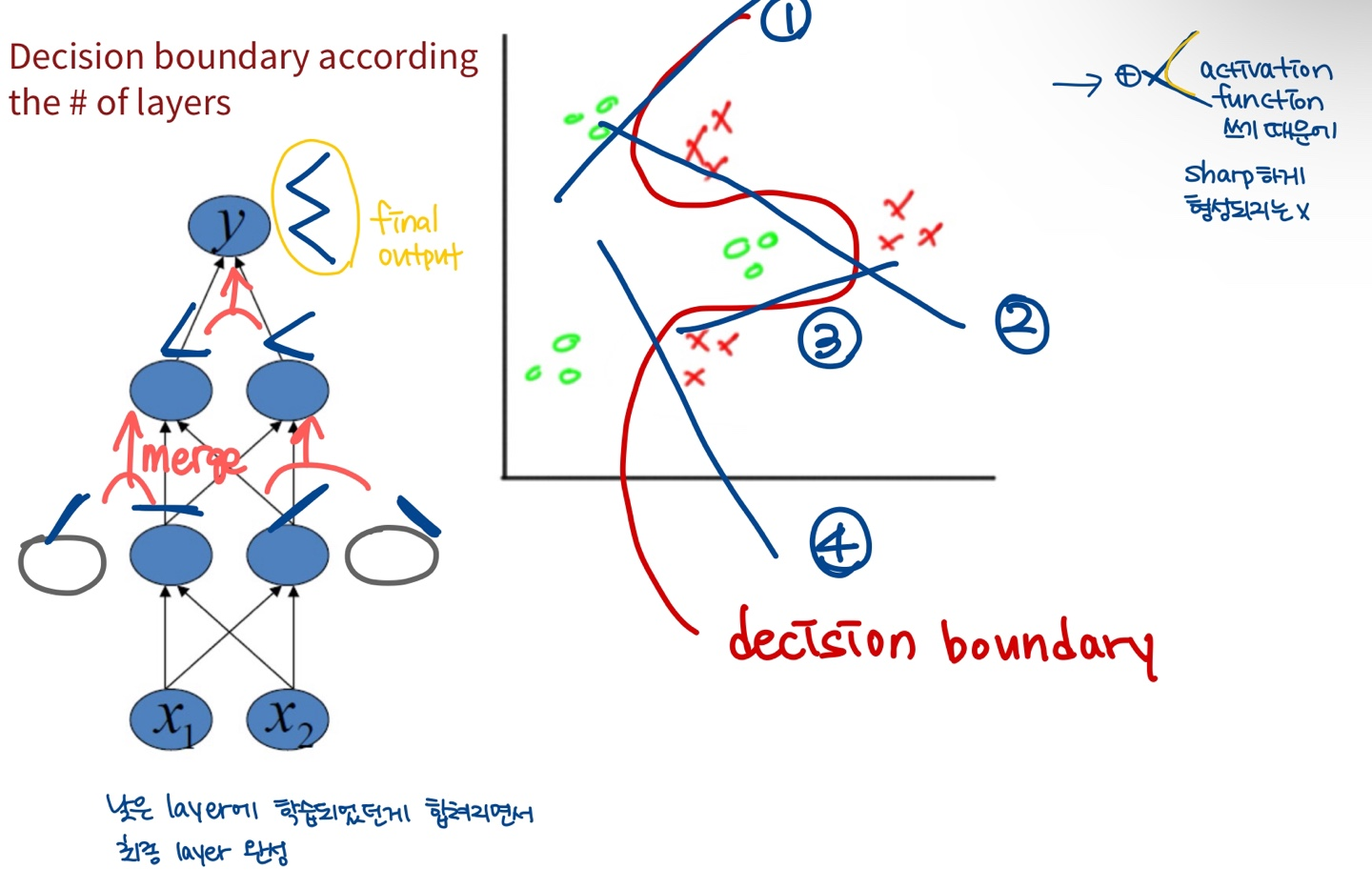
Decision boundary according to the # of layers (hidden layer의 수에 따른 boundary 생성)

• 하나의 hidden layer로는 (==1개의 decision boundary) 문제 해결 x
  
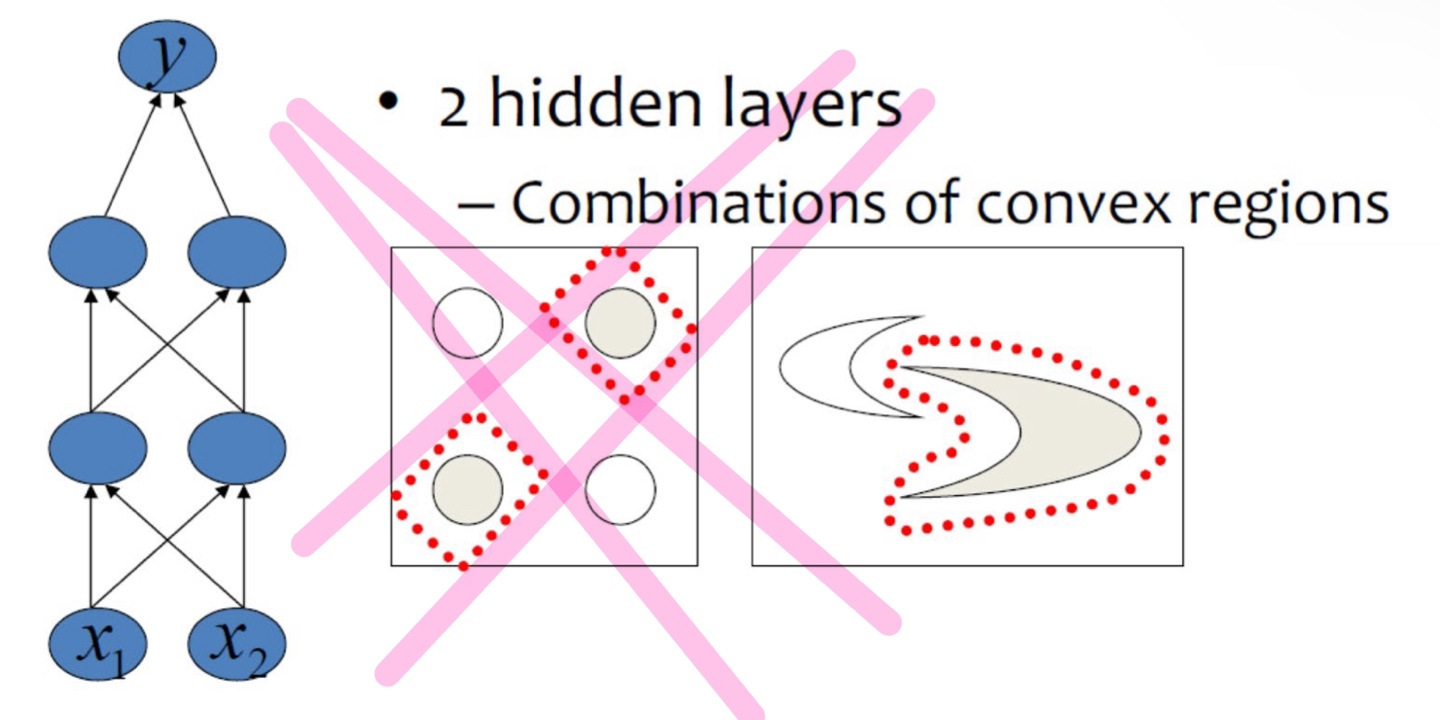
• 두 개로 해결!
  
• 낮은 layer에 학습되었던게 합쳐지면서 최종 layer가 완성됨!
• boundary가 sharp하지 않은 이유: model이 활성화 함수(비선형)를 쓰기 때문에 좀 더 둥글게..(?) 형성이 됨

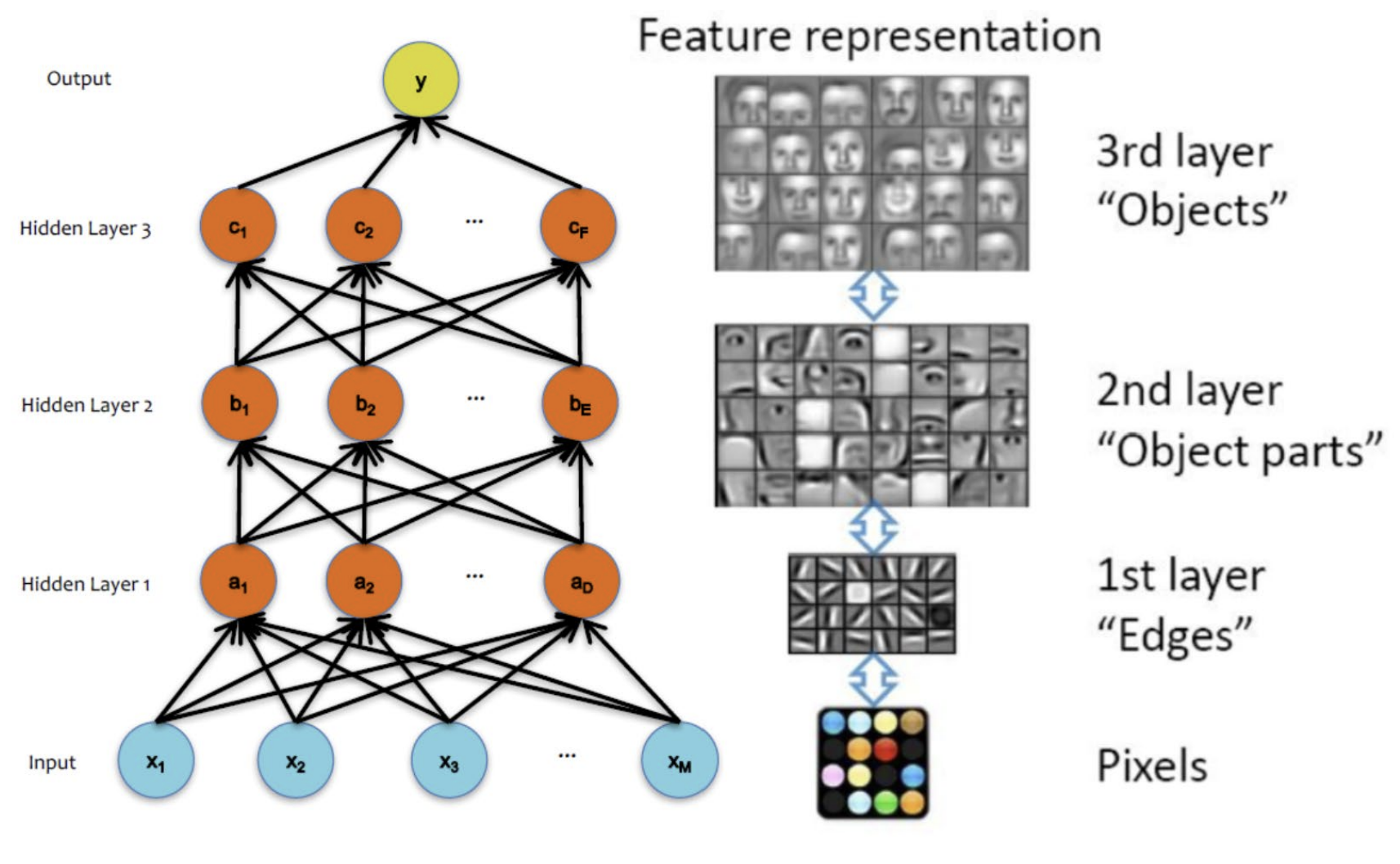
Different Levels of Abstraction (추상화의 수준)

• 저수준 추상화: 하위 layer들은 low level의 특징들을 학습함 (ex. 이미지 처리에서는 엣지(edge)나 텍스처와 같은 단순한 패턴을 추출)
• 고수준 추상화: 상위 layer들은 high level의 특징들을 학습함 (ex. 이미지 처리의 경우, object와 같은 복잡한 수준의 value들을 추출)

NN Architectures

• 1. hidden layers의 수 (==depth)
• 2. hidden layer 마다의 unit 수 (==width)
• 3. activation function의 유형 (== nonlinearity)
• 4. objective function의 형태

+) objective function: 머신러닝 모델이 학습할 때 최적화하려는 목표를 정의하는 함수의 종류 (== 모델이 예측한 결과와 실제 값 사이의 차이를 측정하고, 그 차이를 최소화하는 방향으로 학습이 진행) (== loss function)

sigmoid 함수를 사용한 NN	임의의 nonlinear 함수를 사용한 NN

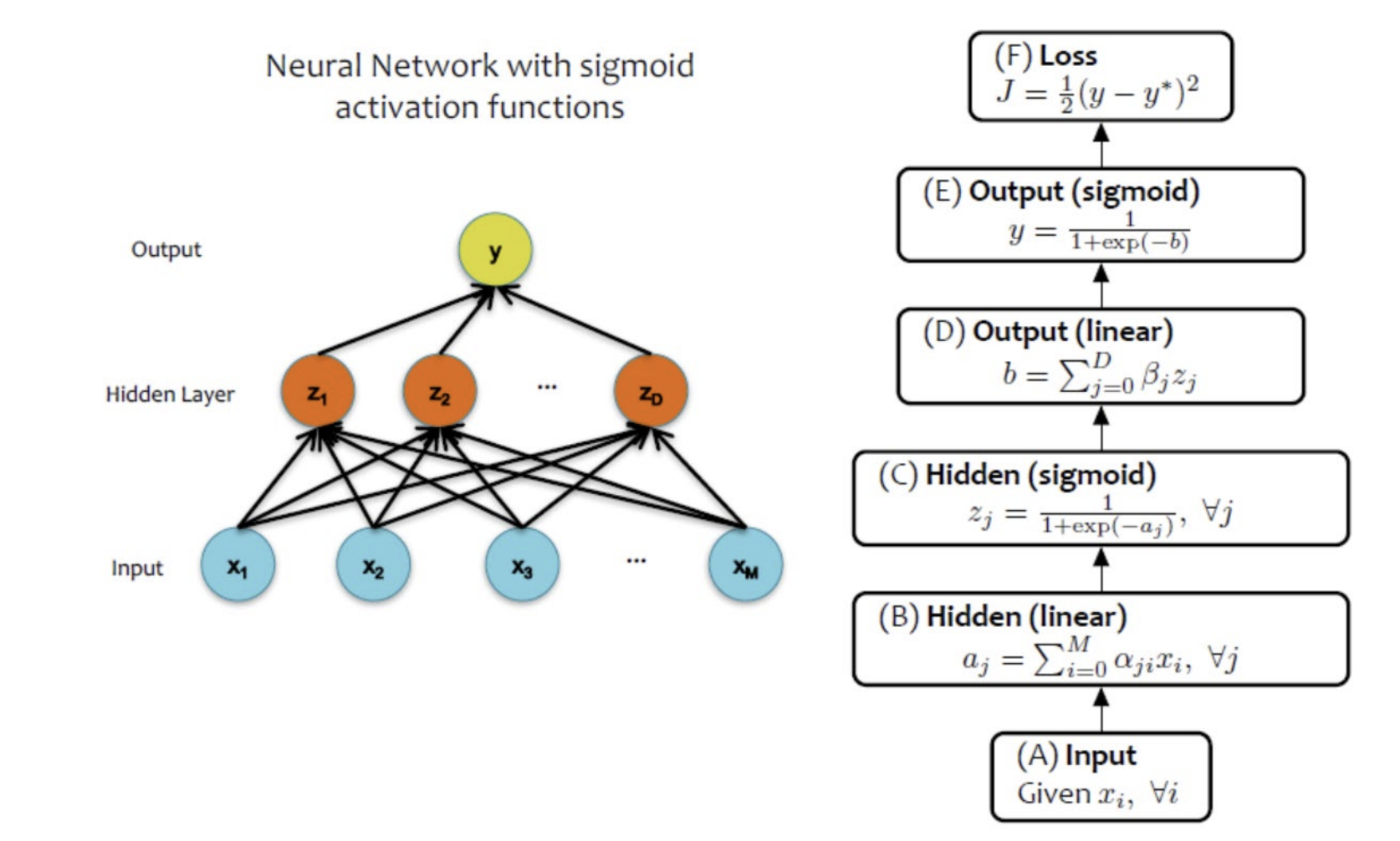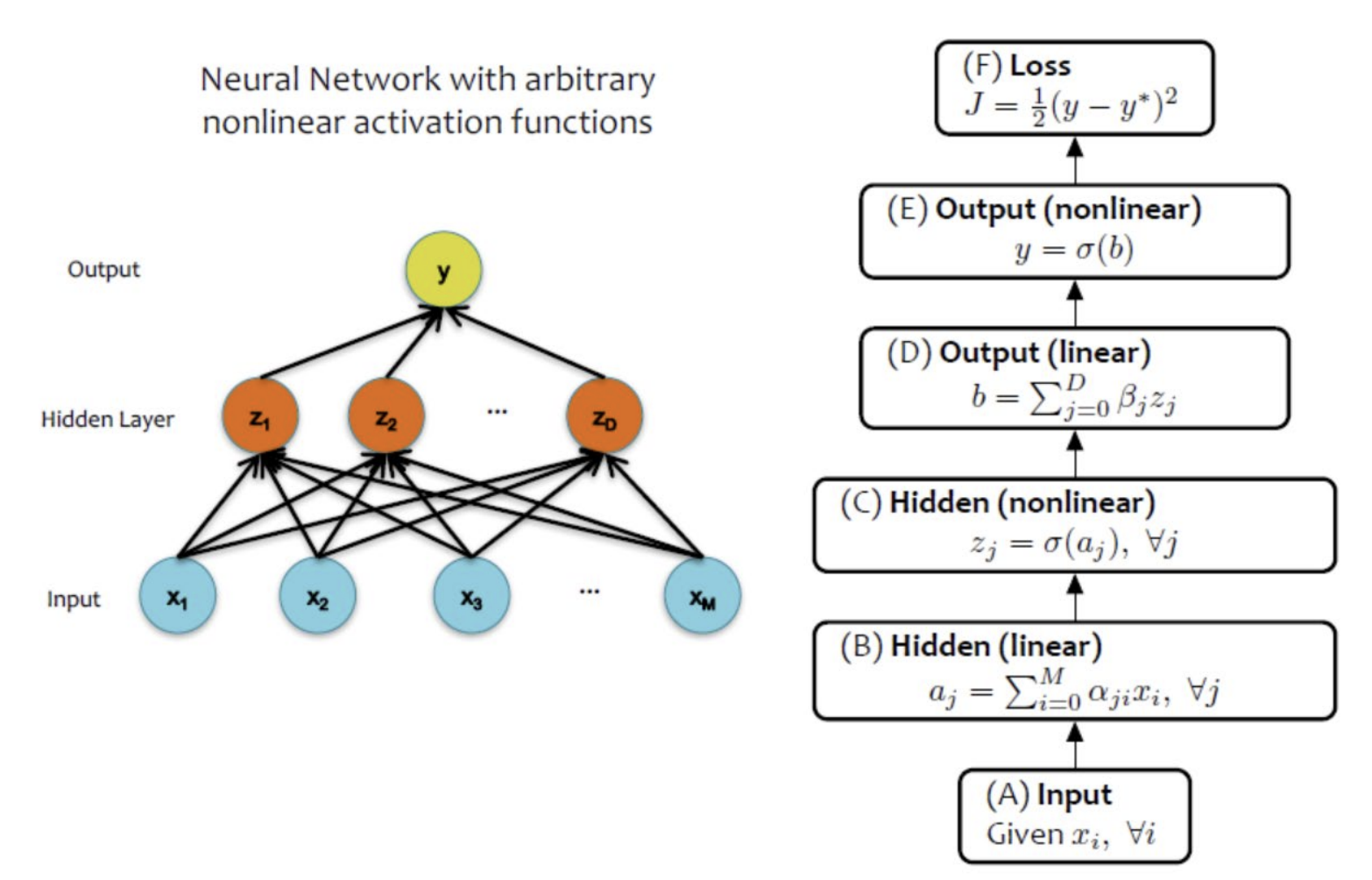Objective Functions for NNs

+) logits scores: softmax 이전의 모델 예측값 (==분류 문제에서 마지막 출력층의 비정규화된 score)
-> 이 값을 softmax function에 적용하면 확률로 변환할 수 있음

• Regression(회귀)
  • 선형 회귀와 동일한 objective 사용
  • 2차 손실(quadratic loss) (ex. mean squared error)
• Classification(분류)
  • 선형 회귀와 동일한 objective 사용
  • Cross-entropy (ex. negative log likelihood)
  • 크로스 엔트로피는 확률(probability)이 필요
    • NN의 마지막에 softmax layer를 추가하기!

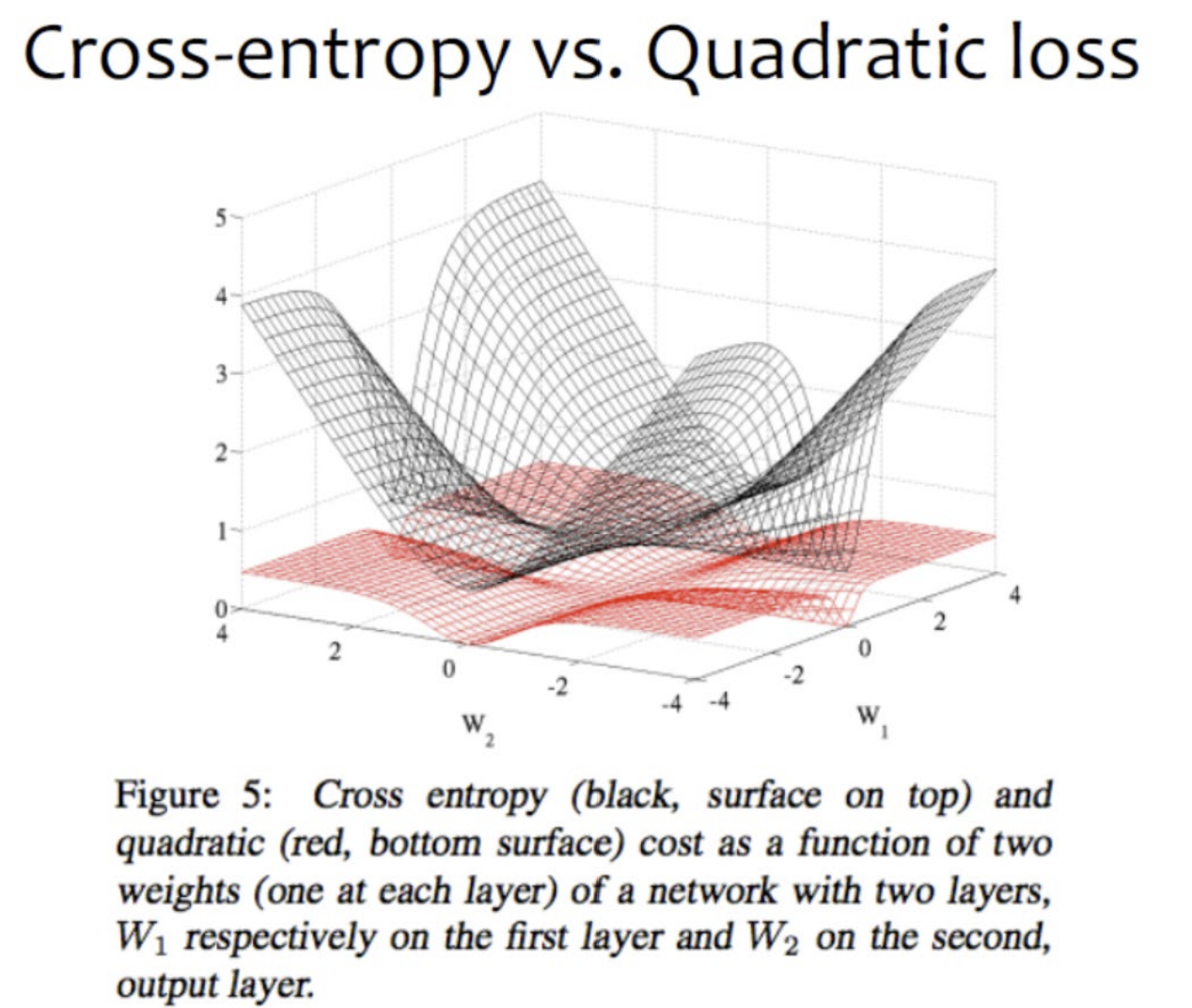
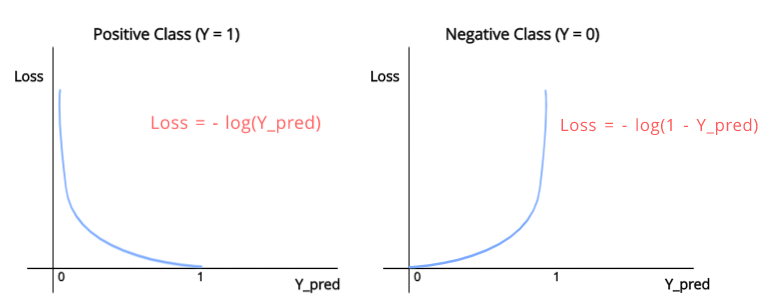
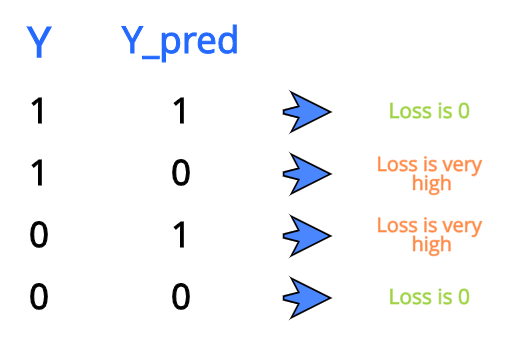
<크로스 엔트로피 loss>

• y를 잘못 예측한 경우(즉, 실제 y가 1인데 0으로 예측했을 시) loss가 infinite로 penalty가 정말 크다
• 검은색 그래프: 좁고 날카로운 decision boundary를 형성
  => classification에 효율적!