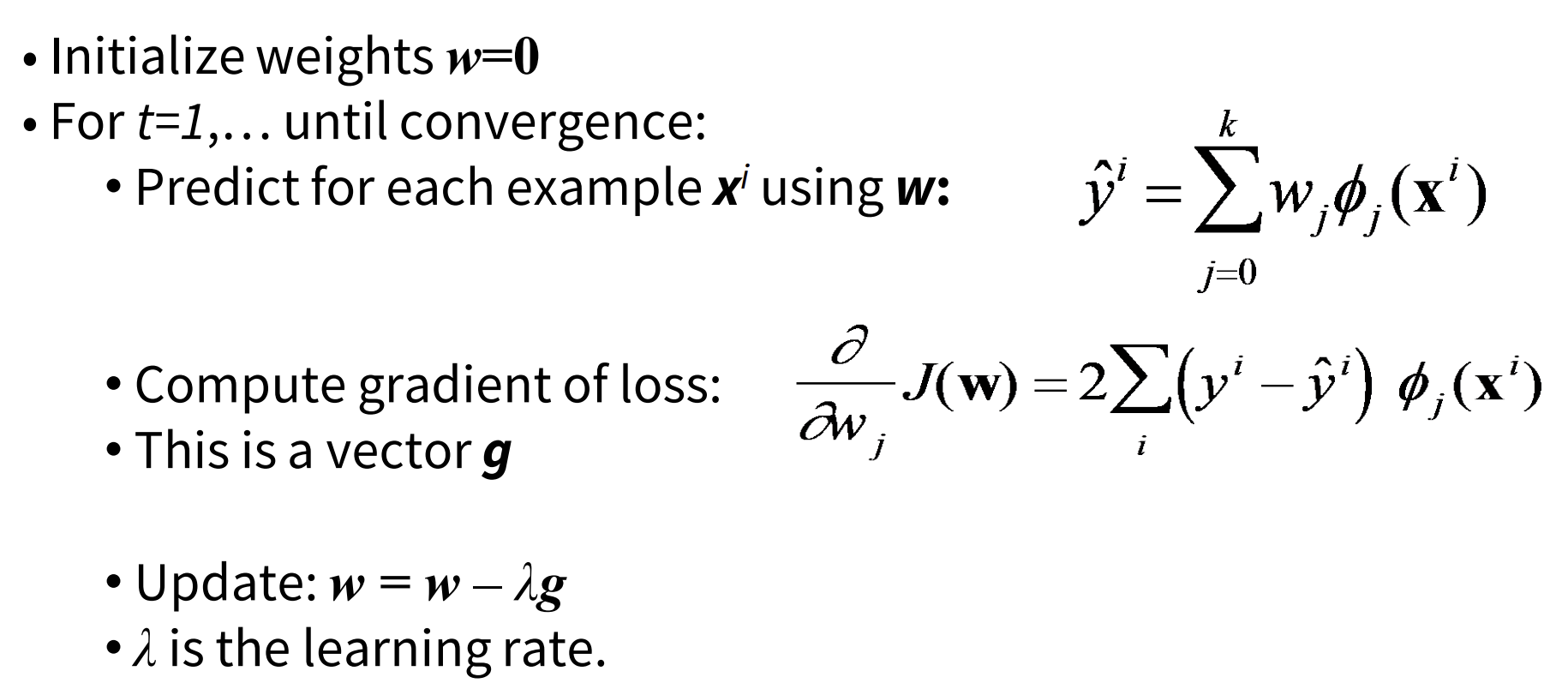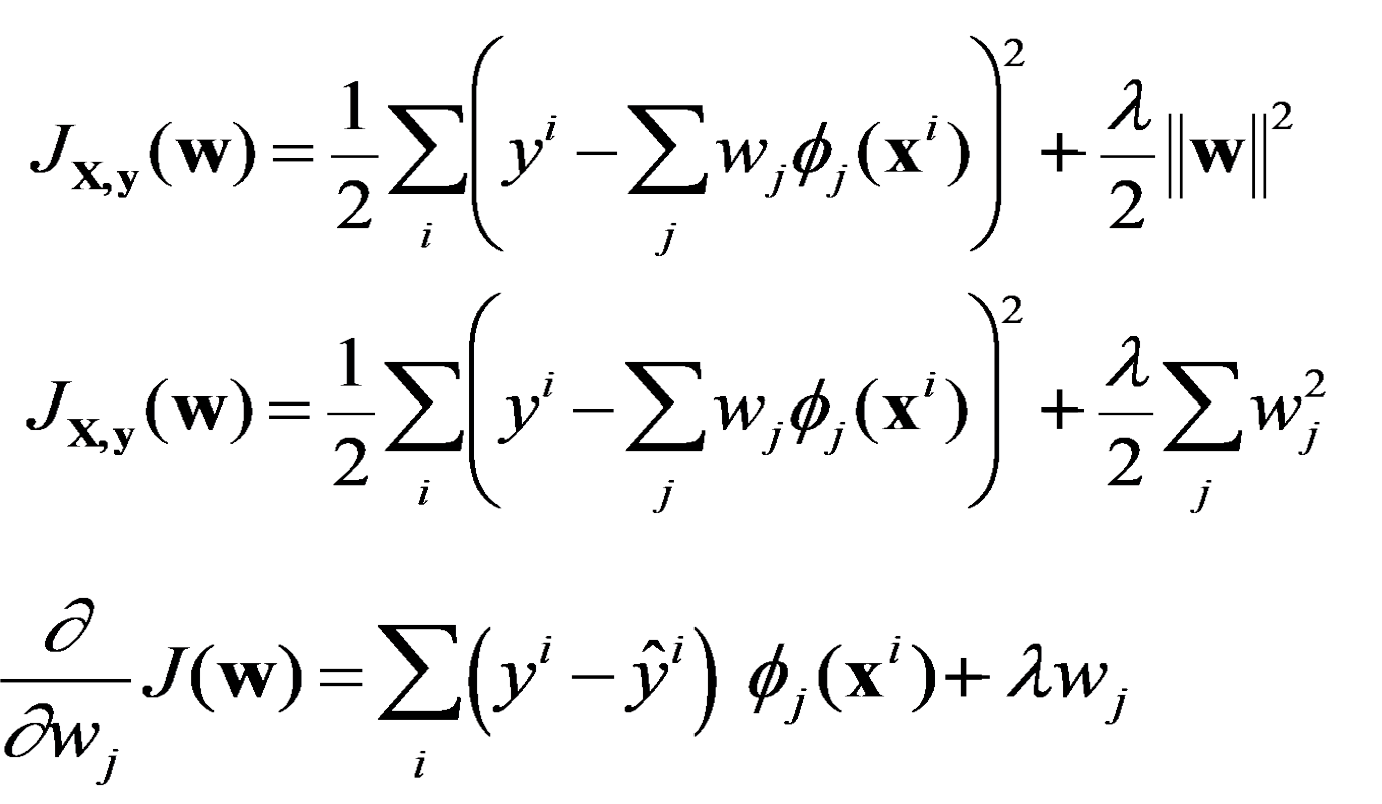- 선형 회귀
- 2개 이상의(multivariate) 독립변수를 경사하강법의 최소 제곱 방법을 활용해 최적화하는 것
- 최적화를 위해 cost function을 각 individual weight(parameter)로 미분함
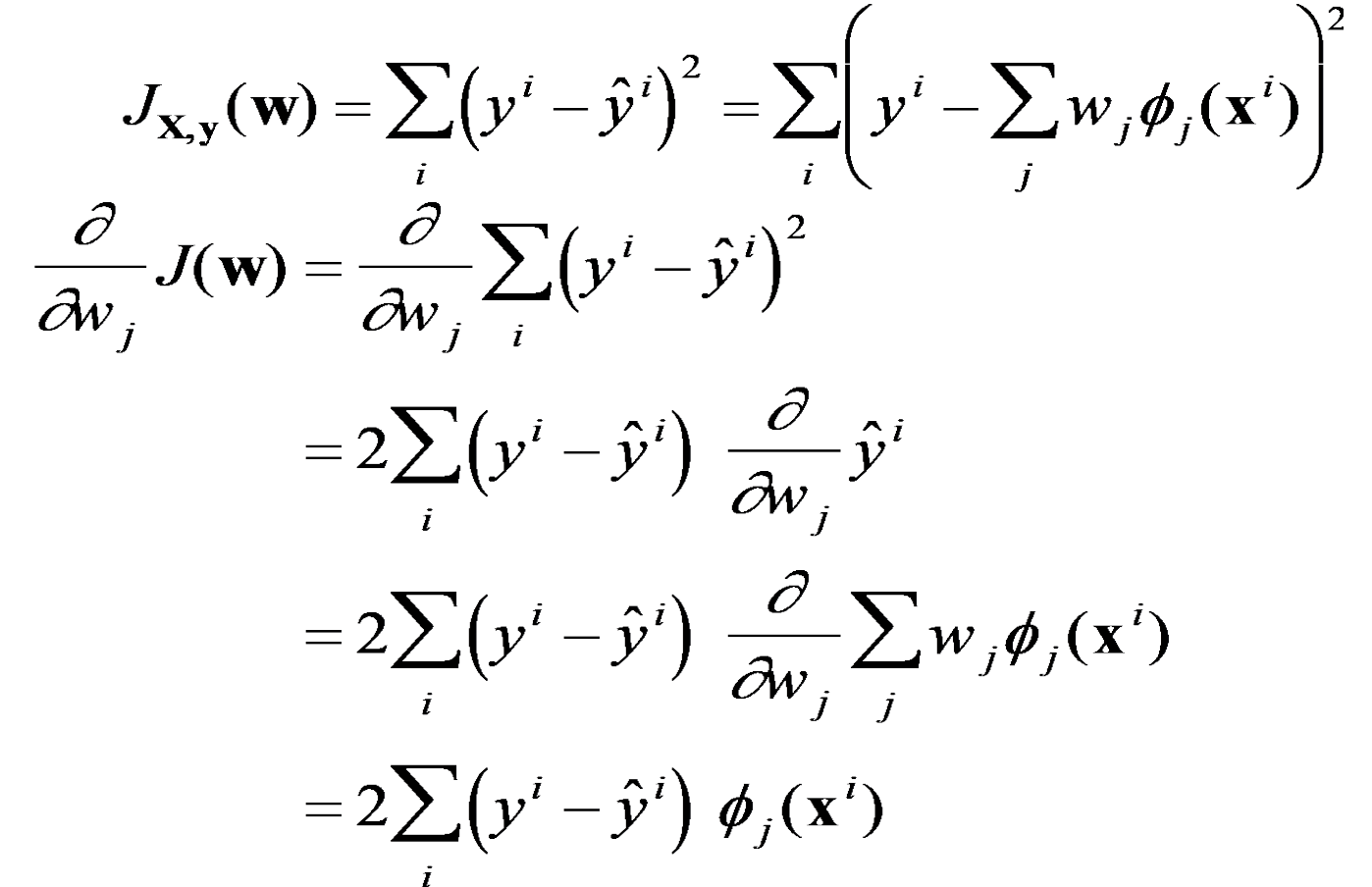
- Learning algorithm
Regression and Overfitting/UnderFitting
- 0차 다항식(0th order polynomial): 상수 함수
- data point들의 fluctuation (==variance)에 비해 모델의 적합도가 현저히 떨어짐 => underfitting
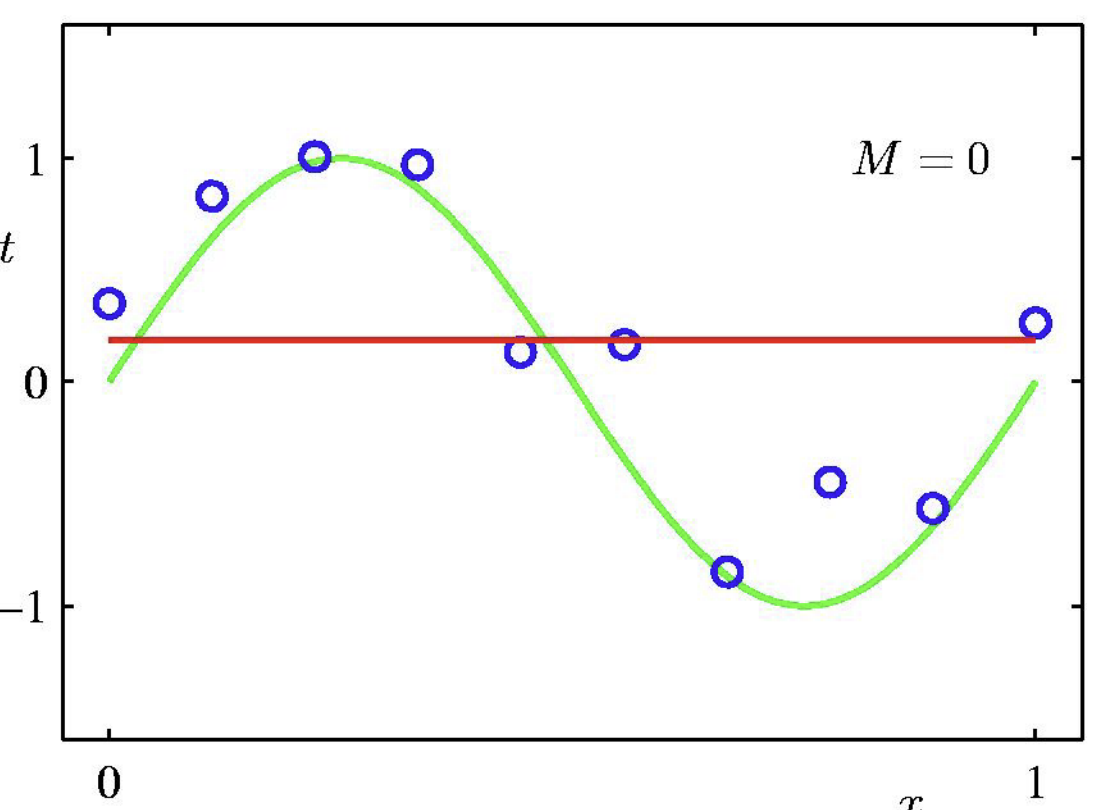
- data point들의 fluctuation (==variance)에 비해 모델의 적합도가 현저히 떨어짐 => underfitting
- 9차 다항식(9th order polynomial) (==표현력 높은 모델) (== 자유도가 높은 모델)
- training data에서는 모두 적합하더라도 새 test data가 나왔을 때 test error가 엄청 큰 문제점이 생김 => overfitting
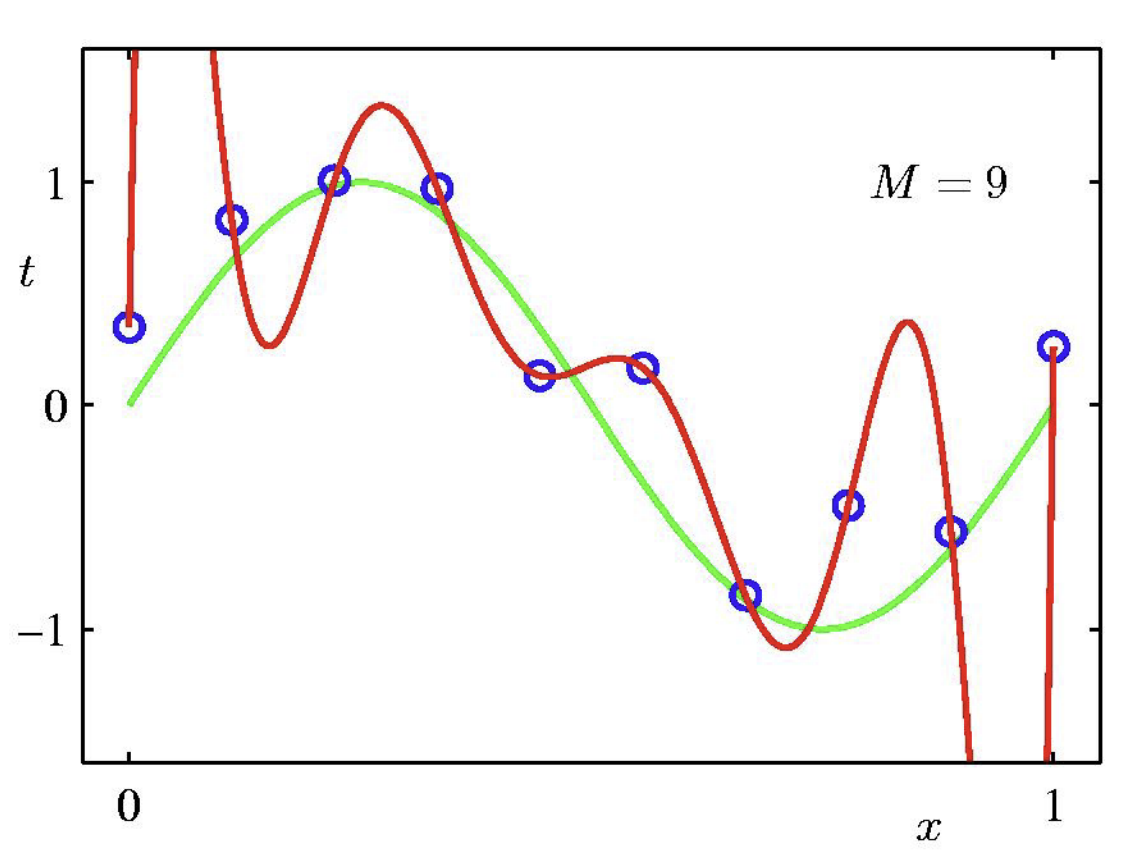
- training data에서는 모두 적합하더라도 새 test data가 나왔을 때 test error가 엄청 큰 문제점이 생김 => overfitting
Polynomial Coefficients

- 이런 w(파라미터)들의 큰 숫자들이 fluctuation을 가져옴
-> 이 계수들의 숫자가 작아지면 model이 더 smooth해진다 - solution: + w²를 강제하면 계수 작아져서 모델입장에서 덜 부담됨(smooth)
Solution
- (근본적인 솔루션) 표현력 높은 모델을 쓸 때, data point의 수를 충분히 높여야함
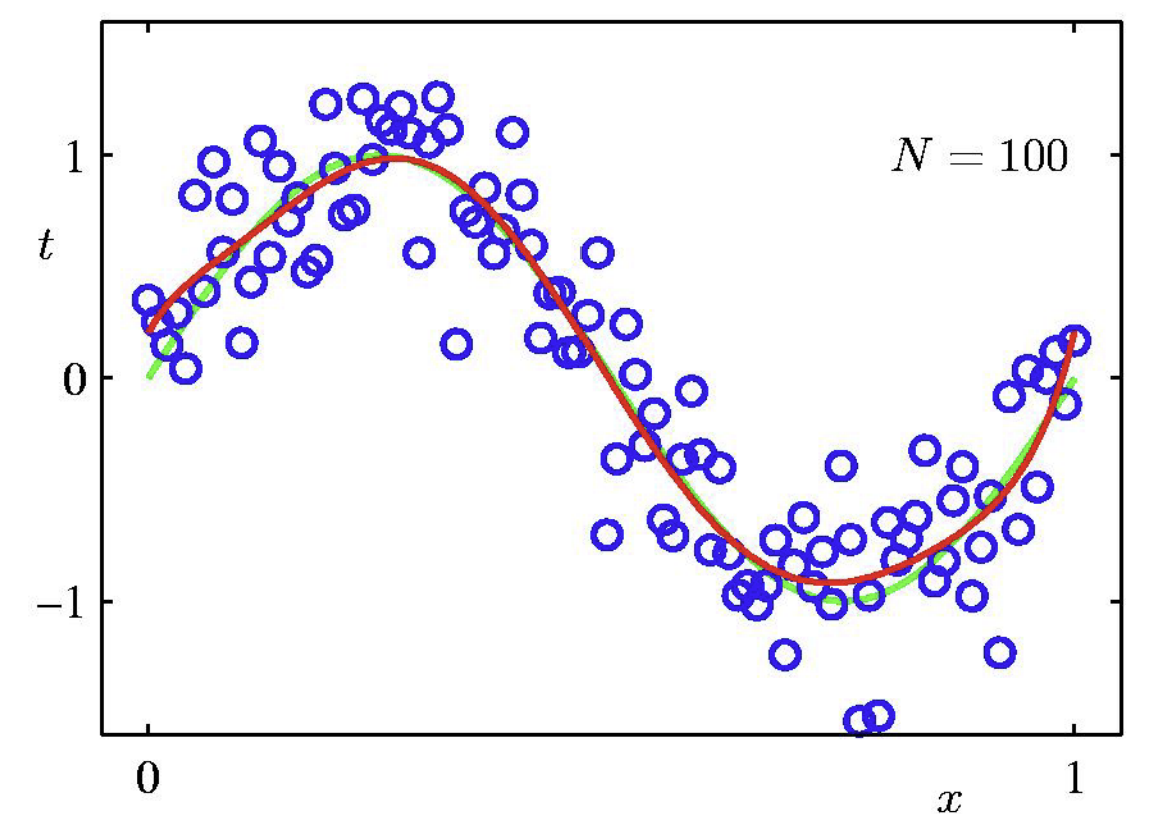
- (근본적인 솔루션) 표현력 높은 모델을 쓸 때, data point의 수를 충분히 높여야함
Regularization
-> 큰 계수의 값에 패널티를 줌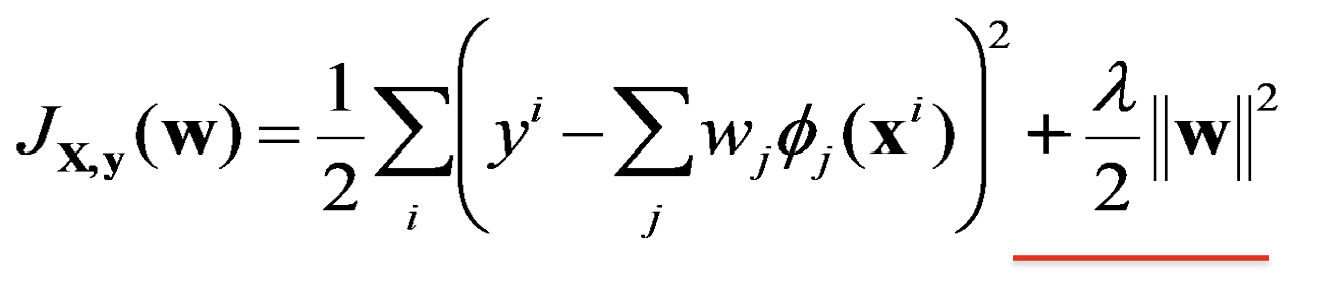
smoothness term == weight를 작게 만든다 == smooth하게 만든다
+람다가 클수록, w²에 강한 weight을 줘서 더 작아짐
🚨적당한 람다를 찾는 것이 중요
Regularized Gradient Descent for LR
- 정규화 term을 추가한 것
- Least-squares curve fitting of an RBF(RBF를 사용한 최소제곱 곡선 피팅)
+)RBF: 방사 기저 함수 = 비선형 함수

How to Prevent Overfitting
① Regularization(정규화)
- 과적합을 막는 방법
- 우리의 목표 : training data를 잘 예측을 하되, 새 data를 잘 일반화하는 모델
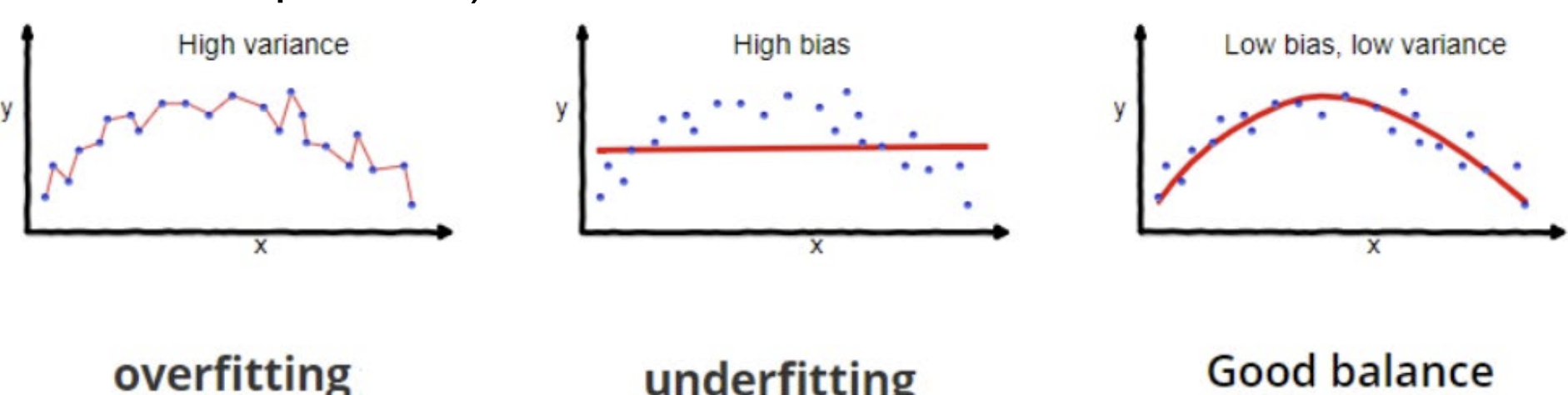
Bias-Variance Tradeoff

- balance fit : high order term을 삭제하여 smooth하게 만든 것
- bias(편향): 고려된 class에서 좋은 가설(hypotheses)가 없을 때 발생
- variance(분산): 너무 많은 가설이 있을 때 발생
- trade-off(절충):
- 더 표현력 있는(expressive) 가설을 선택하면 (==복잡한 모델을 선택하면) 큰 분산/ 작은 편향
- trade-off는 파라미터를 fit하기 위한 데이터 양에 따라 결정된다
(주로 데이터 양은 -> 분산을 완화하는 역할!== overfitting 완화하는 역할)L1 & L2
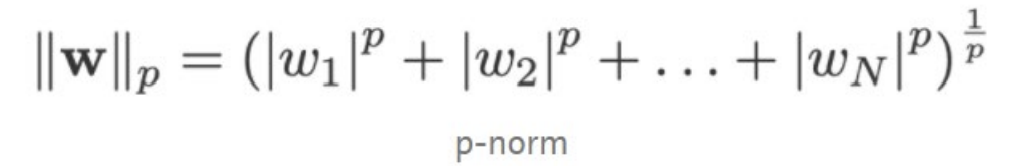
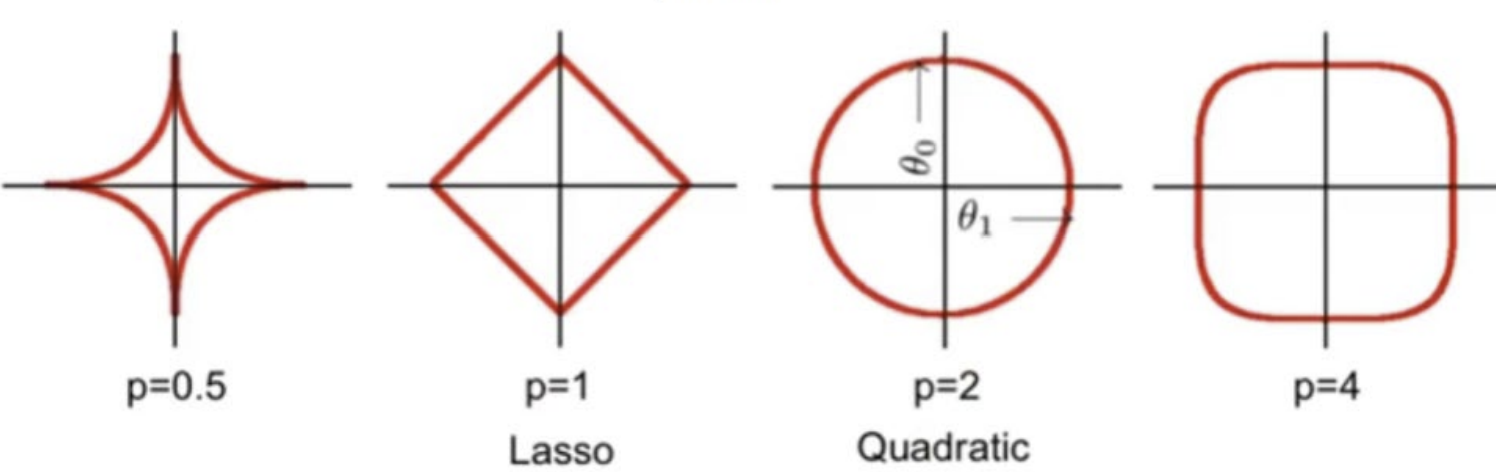
-> 이 p-norm에서 L1 norm과 L2 norm이 파생됨
- 1-norm으로 만든 L1 정규화 term 사용 => Lasso 회귀
- 2-norm으로 만든 L2 정규화 term 사용 => Ridge 회귀
1. L1: 마름모 꼴의 형태로, 가중치가 어느 방향으로 변해도 절댓값의 합이 일정하다는 것을 나타냄
2. L2: 원의 형태로, 가중치가 같은 크기로 변화할 때 비용이 일하다는 것을 나타냄 (모든 방향으로 균등한 저항을 받음) (=가중치들을 고르게 줄이는 안정된 성능)
Lasso (L1: 가중치의 합)
- outlier에 less sensitive => outlier 존재 시 多 사용!
- 작은 값에 더 큰 penalty를 줌
- 0으로 밀어내는 효과가 있음 (== 가중치 중 많은 수가 0이 될 가능성이 높음) (== 특정 변수들의 가중치가 0이 되어 자연스럽게 중요한 term만 선택되는 효과가 있음) (==희소한 해) => sparsity(희소성) 효과
Ridge (L2: 가중치의 제곱)
- 제곱을 하기 때문에 잘못된 outlier가 존재할 때 정규화 term이 너무 커짐 (== outlier에 sensitive)
- 큰 값들을 우선적으로 공격하는 특성 (큰 값에 더 큰 pelanty를 줌)
② Cross-validation
-
교차 검증: 초기 훈련 데이터를 -> 여러 개의 mini train-test로 분할하여 모델을 조정(tune)하는 것
-
Why?

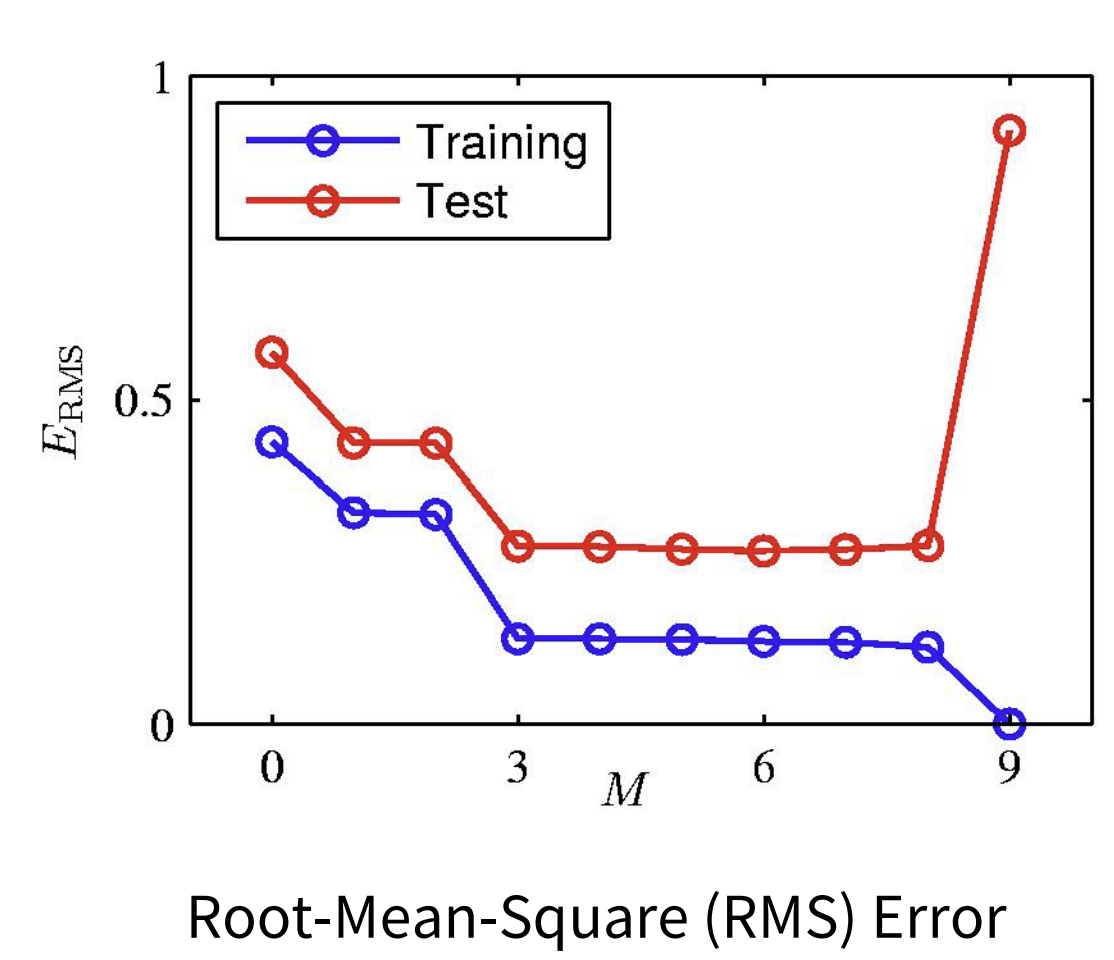
training error는 m차 다항식이 커질수록(==복잡해질수록) 감소
but test error는 m차가 커질수록 처음에는 감소했다가 증가하게 됨
=> cross-validation의 필요성
- validation(유효성 검사) set에서 좋은 가설(모델)을 찾기
- train과 validation으로 쓰이지 않은 test set에서 편향되지 않은 결과 얻어내기
1) 훈련 및 검증 set: 올바른 예측 변수를 찾는 데에만 사용
2) test set: 알고리즘의 예측 오류를 확인하는데에만 사용
=> 이 과정을 여러번 반복하여, 결과의 평균을 내어 오차 추정치를 제공함
Leave-one-out cross-validation
1. 다항식(polynomial)의 각 차수(order) d에 대해:
(a) 다음 절차를 m번 반복:
1) training set에서 i번째 instance를 제외 시킴 -> validation set으로 사용
2) 다른 모든 instance는 가장 좋은 W(파라미터)를 찾기 위해 사용
3) 남은 instance를 예측하는 데 발생하는 오류를 측정(비용함수 ;J)
4) J = 대부분 편향되지 않은 실제 예측 오류를 나타냄
(b) 예측 오류의 평균을 계산함
2. 가장 낮은 평균 추정 오류를 내는 차수(d)를 선택함
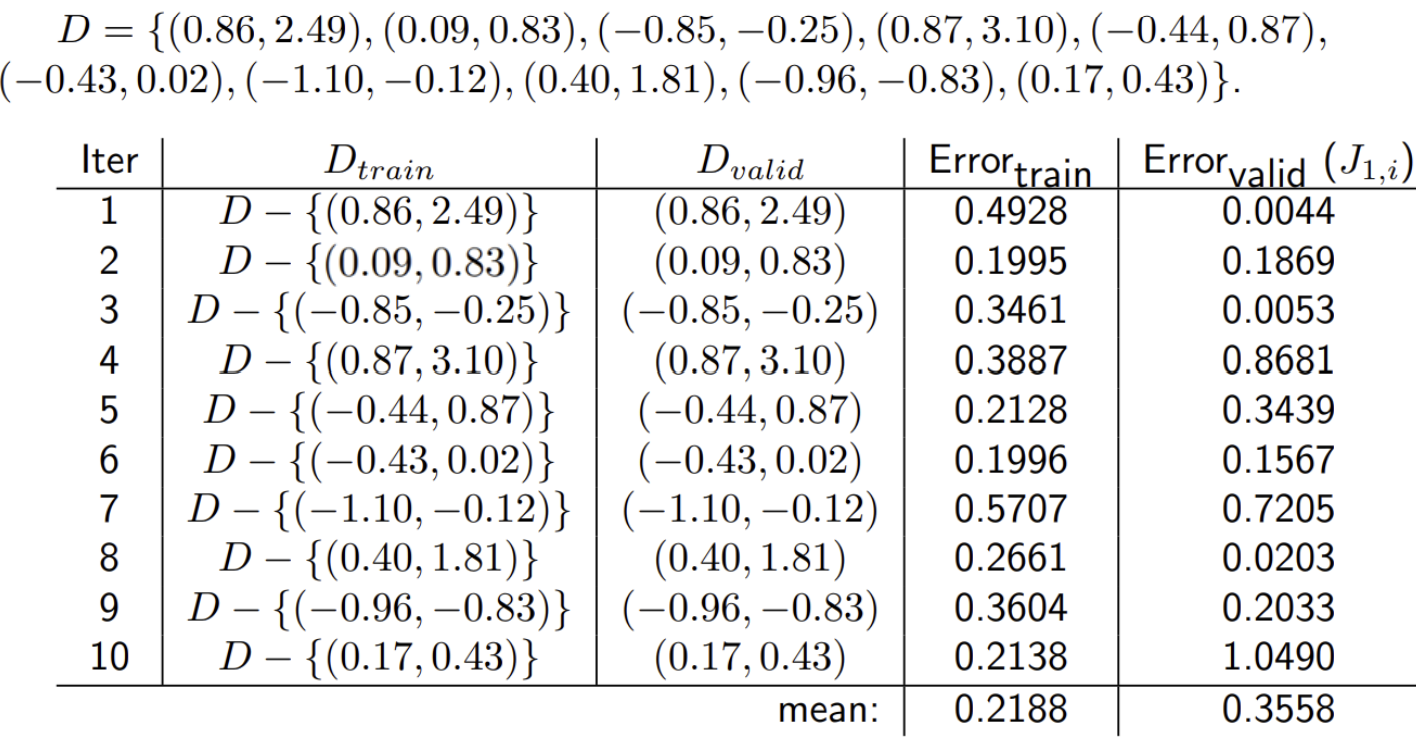
leave-one-out cross-validation ex
- 전체 dataset D에서 train과 valid를 나누어서 train error와 validation error를 계산함 => 차수를 늘려가면서 반복 ~~
- d(차수)가 증가할 수록, train error는 감소하지만 일정 d(==여기서는 2)d을 넘어가면 validation error는 증가함 -> overfitting 문제
- 따라서, 최적의 d는 2이다
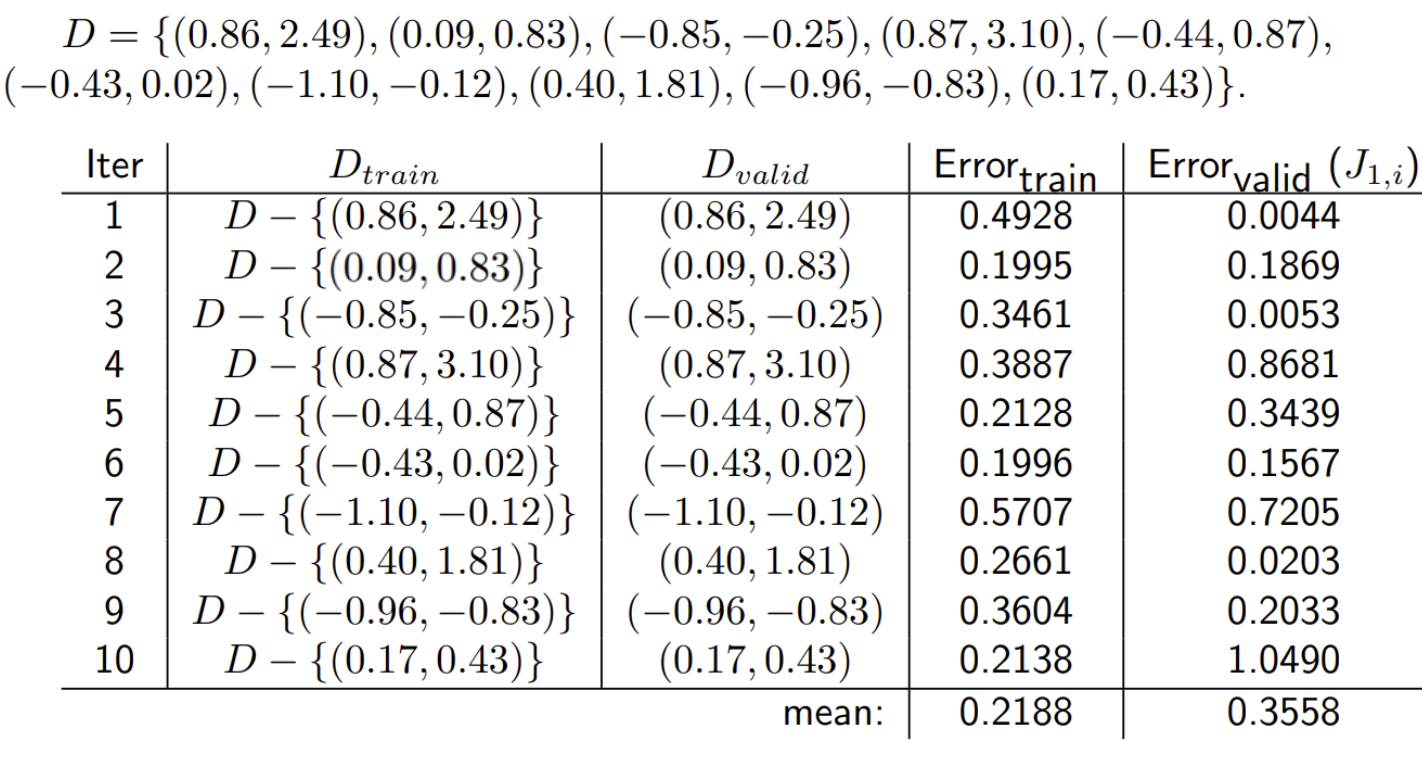
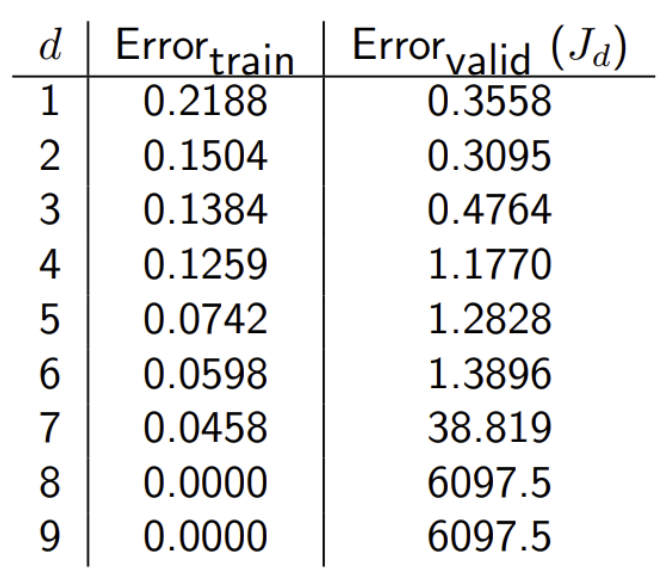
- 구현(implement) 쉬운 알고리즘
- 실제 오류에 대한 휼륭한 추정치를 제공함 (validation error를 사용함으로써)
- 여러 알고리즘을 사용할 때 dataset 내의 문제가 있는 ex(outlier)를 나타낼 수 있음
- 계산 비용은 instance의 수에 비례하므로 최적의 predictor를 찾는 것이 비용이 많이 든다
- 하나가 아니라 여러 개의 predictor를 얻음
- 대안: k-fold cross-validation (dataset을 k개의 부분으로 나눈 다음 진행하는 것)
③ Train with more data
- data가 많을 수록, 더 복잡한 hypotheses space를 탐색할 수 있으면서도 좋은 solution도 갖게 됨
④ Remove features
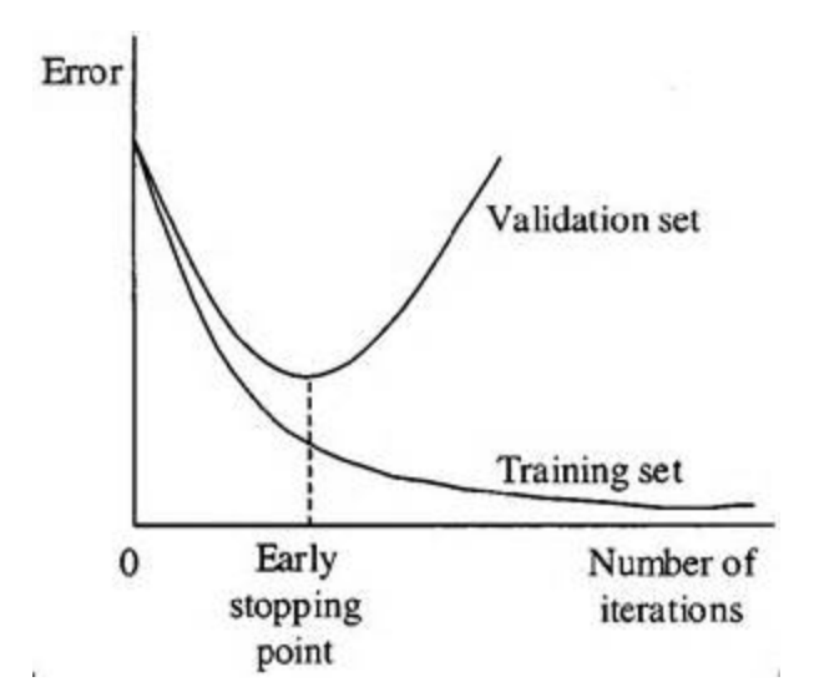
⑤ Early stopping