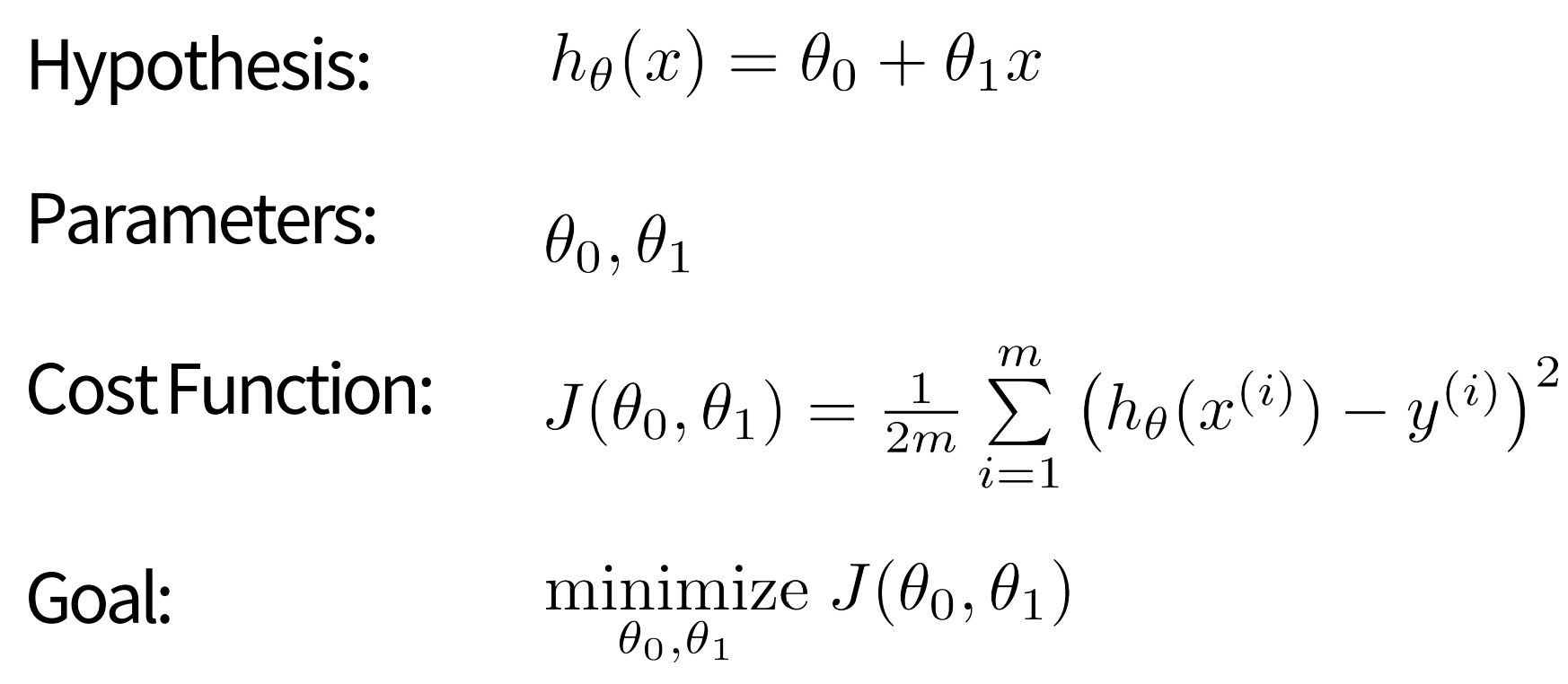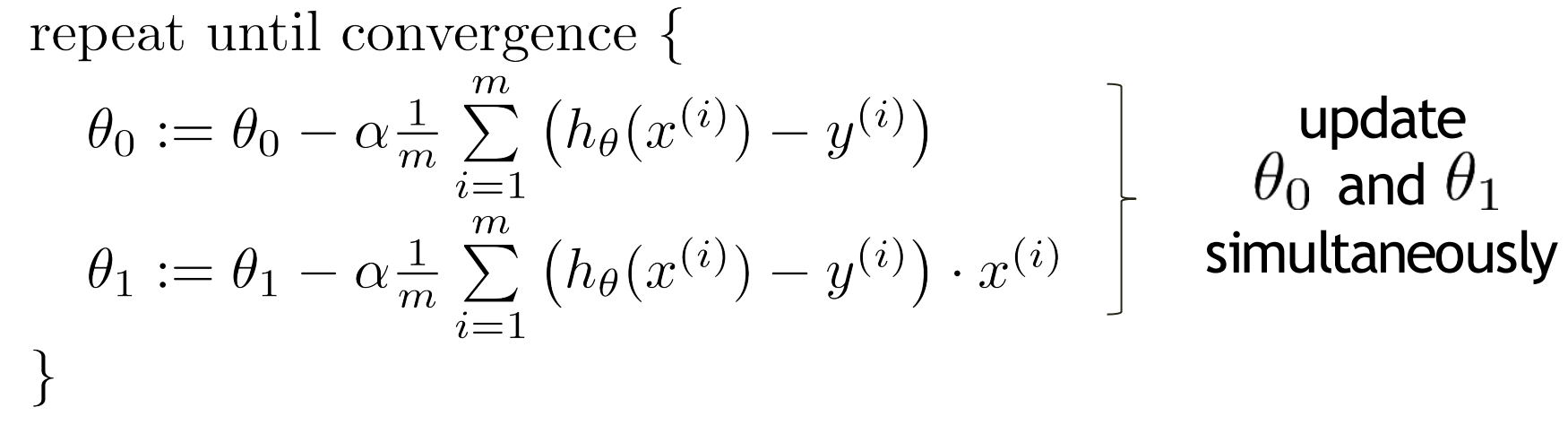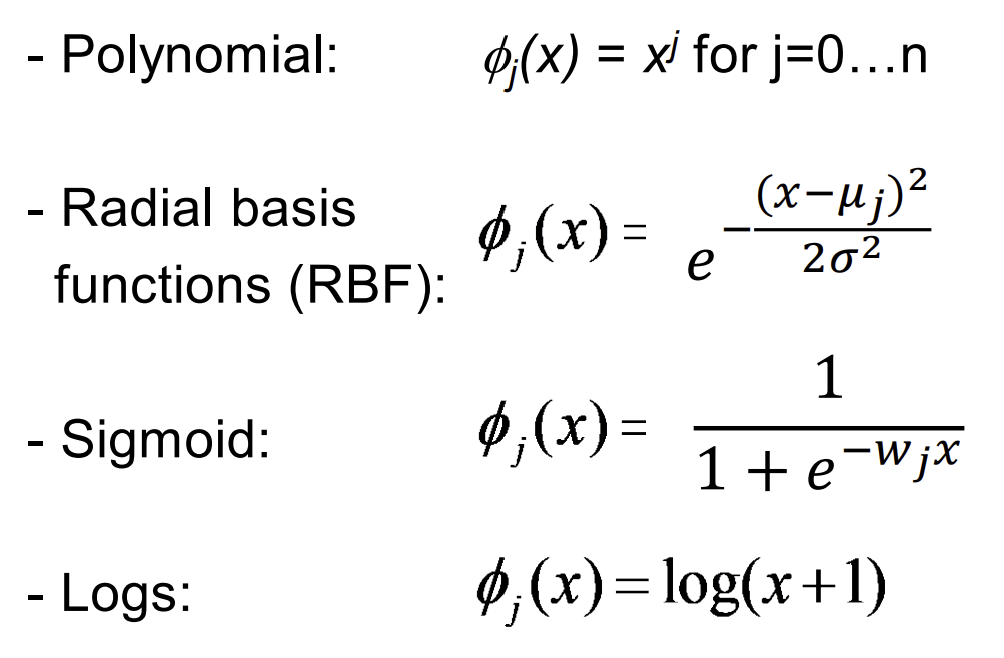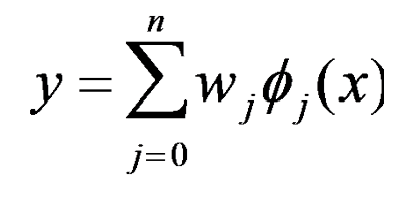Gradient Descent
- 최소값(minimum)에 닿을 때까지 J(세타) (== 비용함수)가 작아지는 방향으로 파라미터를 계속해서 바꿔나가는 것
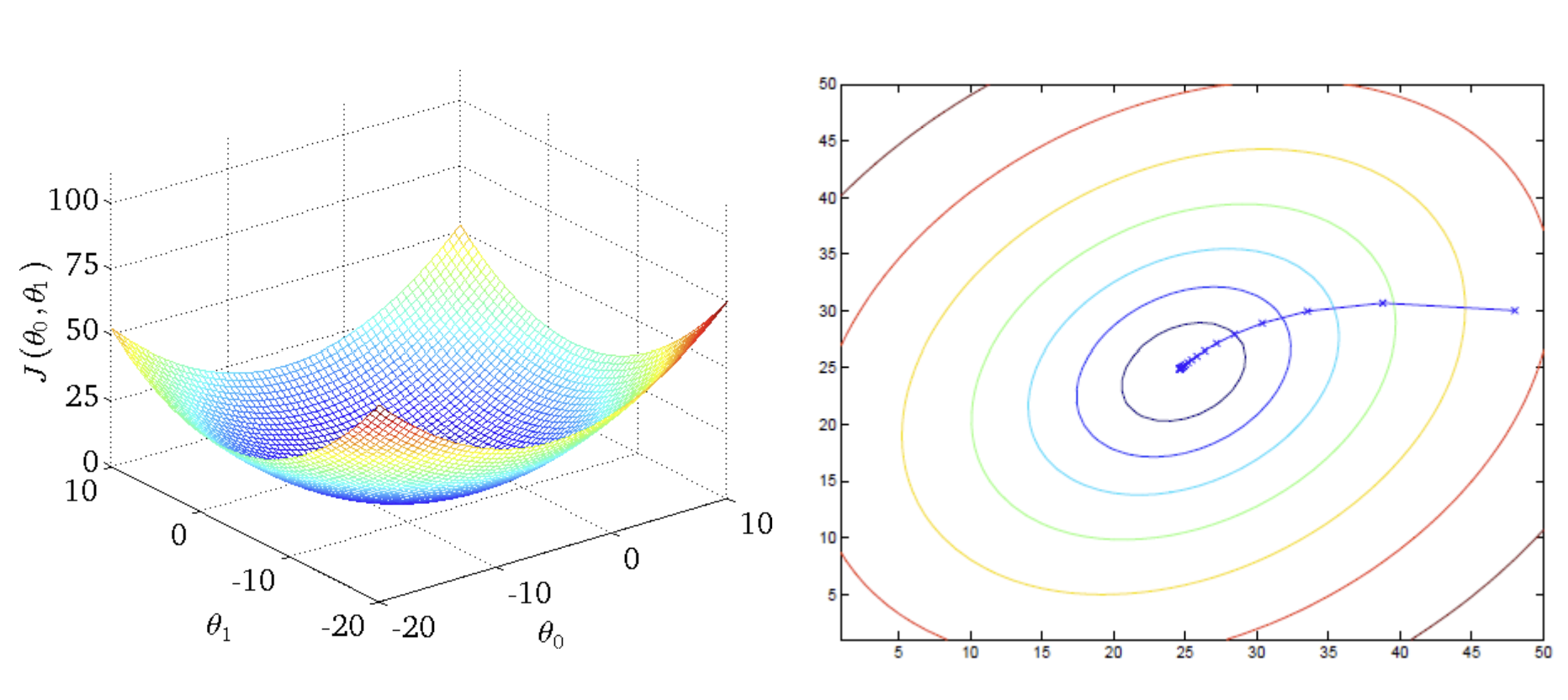
🚨 주의: 반드시 global minimum point로 가는 것이 아니라 local min으로 빠질 수도 있음 => strating point 설정 중요!- 비선형 최소제곱이나 비볼록 최적화 문제에서는 해를 찾아갈 때, zigzagging 특성이 드러남
- 우리가 다룰 선형 회귀에서는 only single global min을 가짐! (명확한 답)
=> convex optimization problem (볼록 최적화 문제)
Gradient descent algorithm
- 두 개의 파라미터(세타1, 세타2)를 업데이트함 (J(세타) = gradient = which way to go)
- 알파: 움직이는 rate = magnitude (how big a step to take)
알파가 너무 ↑ ~ 미니마에 도달하지 못함 (divergence)
알파가 너무 ↓ ~ 수렴하기까지 오랜 시간이 걸림
🚨 단, 세타 2개를 한꺼번에 업데이트하는 것이 중요함
Batch Gradient Descent; BGD
- m개의 sample로 업데이트하는 것
👍
+계산 효율성 (한꺼번에 gradient==평균 계산 가능하므로)
+convergence(수렴) 안정적임
👎
-로컬 미니마로 수렴할 수도 있음
-각 epoch별로 전체 dataset을 사용할 수 있어야함
Stochastic Gradient Descent; SGD
- only 한 개의 sample로 업데이트하는 것
👍
+BGD보다 빠름 (순차적으로 data를 처리하므로)
👎
-업데이트의 빈도(frequency)가 수렴에 영향을 미치는 기울기에 noise를 유도
=> 개별적인 sample의 noise를 최적화 process에 반영하므로
but, 👍순기능: noise가 로컬 미니마를 빠져나오기 위한 변화를 일으킬때도 있음
-잦은 업데이트로 인한 계산 비효율성
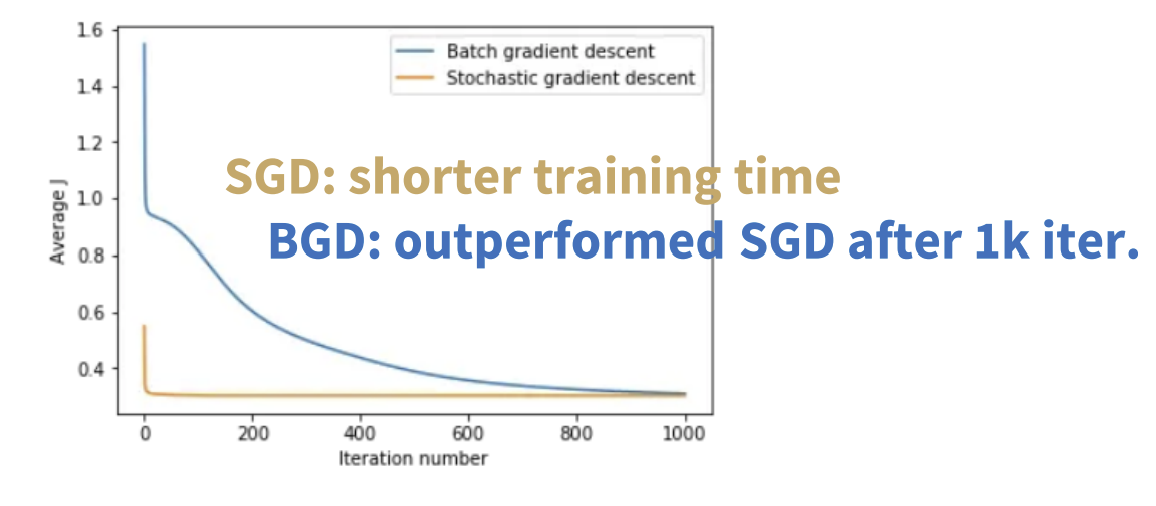
Comparison
- 평균 비용함수(average J) 비교
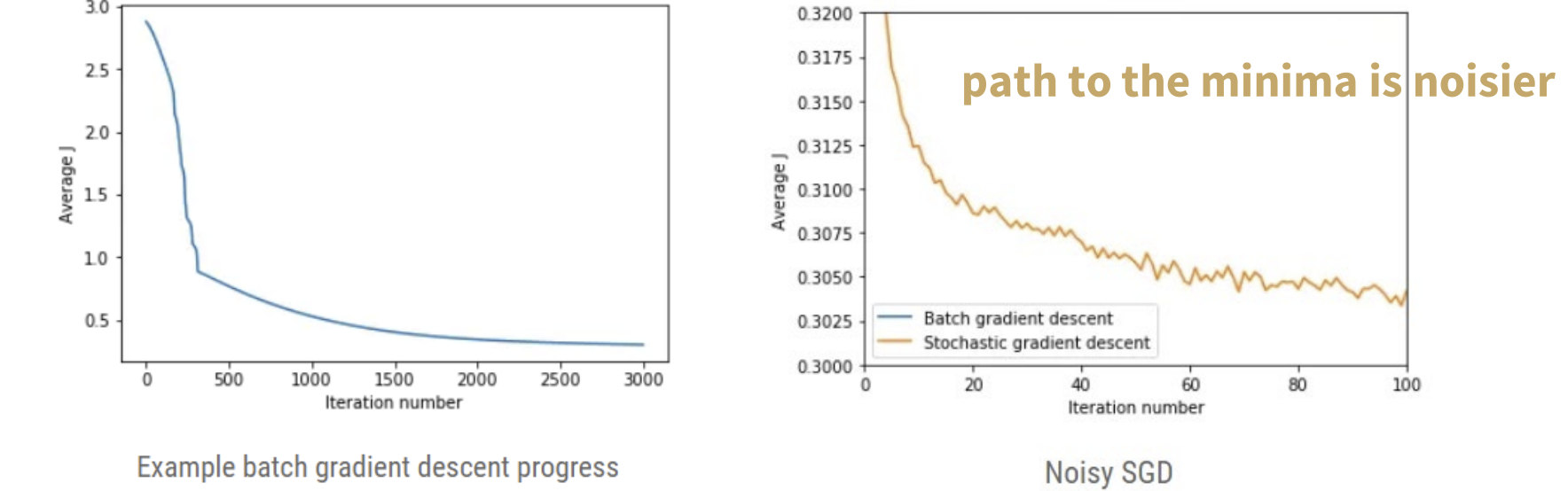
-> 1k 넘으면, SGD의 비용함수가 더 올라감 (BGD가 더 안정적)
- SGD가 미니마 찾는 과정에서 많은 noise를 발생시킴을 알 수 있음
Mini-batch gradient
- BGD(몽땅)과 SGD(1개)의 사이
- n개의 data point를 각 반복에서 사용함
- batch의 size가 중요한 파라미터로써 작용함
선형 회귀에서의 경사하강법 수식 정리
- 기본 수식
Linear regression with multiple variables
-
ex. y(output)이 코스닥 주식 가격일 때, several input은 네이버/삼성/엘지 등의 주식 가격
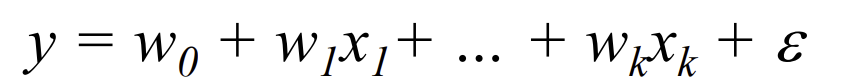
-
모든 함수가 line, hyperplane(평면)이 아니지만!
=> 계수(coefficient)가 선형이면 여전히 선형 회귀 문제이다!
Non-Linear basis function
- input이 linear가 아닐 경우 -> input을 가공하여 사용하면 됨
- 기존에 알던 x1,x2같은 value가 아니라 z=x1x2와 같은 새로운 변수를 추가!
=> multi-value linear regression(다변수선형회귀) 문제로 해결 가능
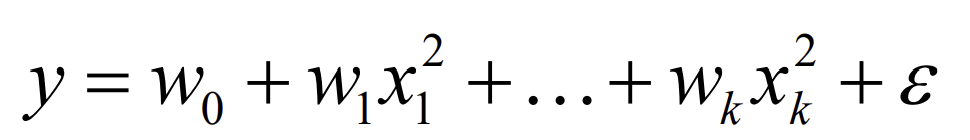
Q. intercept W0을 만드는 방법은?
A. z=1(z1)로 두고 w0를 곱하여 만들 수 있다!
- 비선형 함수의 예시
- input의 모든 함수를 사용할 수 있음
- 회귀 파라미터에 대한 솔루션은 동일하게 유지됨
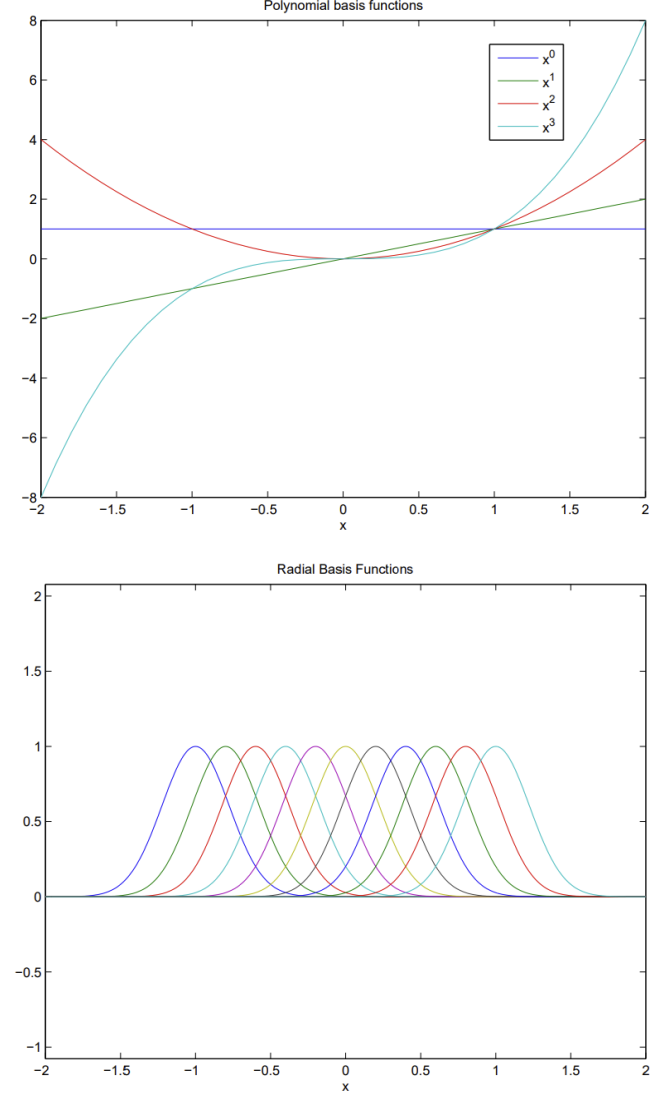
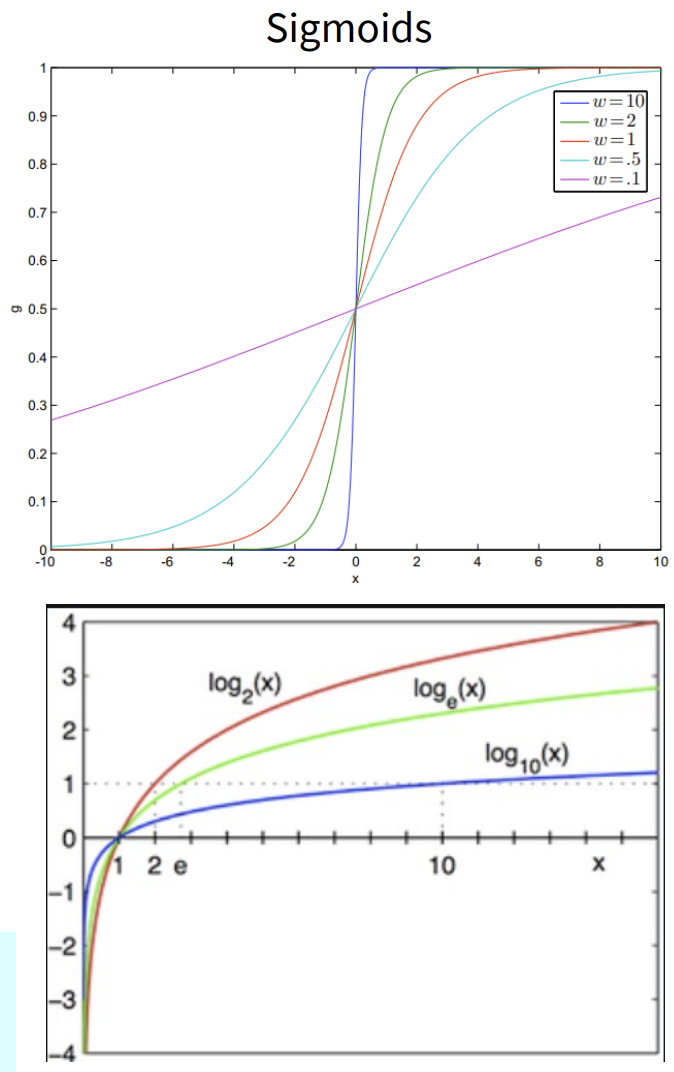
일반적인 선형 회귀의 문제
- 선형 회귀의 basis function(기저함수) notation : ϕ (파이)
- ϕ : 다변수 회귀일 경우 xj 혹은 비선형 기저함수일 수도 있음
- ϕ=1이면, 절편(intercept)의 항임