[NLP 13] RNN(Recurrent Neural Network) 3 : RNN 심화 이론

순환 신경망 - RNN (Recurrent Neural Network)

• 입력 데이터의 순차적 특성을 학습하기 위해 반복 구조를 사용하는 신경망
• 이전 상태의 정보를 현재 상태로 전달하며, 시계열 데이터, 자연어 처리 등 시간적 의존성이 있는 데이터를 처리하는 데 적합함
• 입력과 출력이 시간에 따라 의존적이므로, 이전 단계의 정보를 다음 단계에 피드백하는 구조를 가짐

---

• 데이터 전처리(토큰화 등)을 할때 데이터 벡터사이즈를 동일하게 맞춰주는것이 중요함

---

RNN의 입력층 (Embedding layer)

• 시점 $t$에서의 입력 $x_t$를 받음 (텍스트의 경우 단어 또는 단어 벡터를 입력 받을 수도 있음)

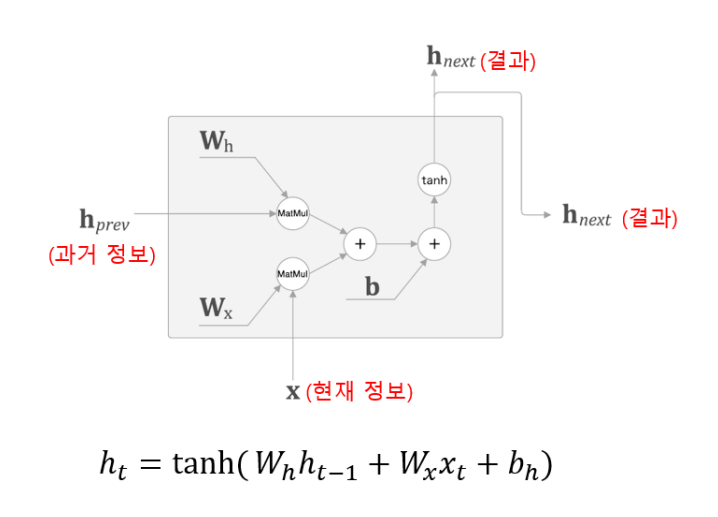
RNN의 은닉층 (RNN layer)

• 은닉상태(hidden state) $h_t$는 시점 $t$에서의 입력 $x_t$와 이전 시점 $t-1$의 은닉 상태 $h_{t-1}$를 결합 하여 계산됨
  • $h_t$는 $h_{t-1}$와 현재 입력$x_t$를 결합하여 다음 시점에 전달되며, 이전 모든 시점에서 축적된 정보를 포함하여 은닉 상태를 유지함
    
    
• RNN layer 기본 구조

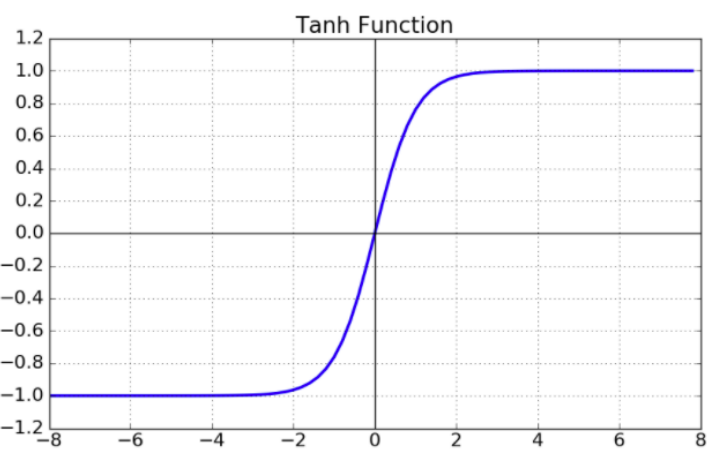
• 은닉층의 활성화 함수 (tanh - 하이퍼볼릭 탄젠트)
  • RNN의 대표적인 활성화 함수 (tanh Function)
    • 다른 모델같은 경우에는 잘 쓰이지 않음
  • tanh Function : 시그모이드 함수와 비슷, 출력 값이 -1과 1사이에 존재
    

---

• 가중치 행렬(W)
  • $W_x$ 와 $W_h$는 일반적으로 값이 다름
  • $b(bias)$에 경우 모델이 학습하면서 자동으로 조정되는 값임

Q) RNN layer에서 $W_h$를 곱하는 이유는?

• $t$가 진행될 수록 $W_h$를 해주지 않으면 벡터값이 그대로 계속해서 늘어남(벡터의 나열) 그렇기 때문에 과거의 값들 전부 묶어서 하나의 벡터로 압축하기 위해 $W_h$를 곱하는 것
  
  
• 만약 $W_h$를 곱하지 않고, 단순히 입력 벡터를 더하기만 하면, 이전시점($h_{t-1}$)의 정보가 현재 시점 $t$의 계산에 반영되지 않게 됨 즉, RNN의 설계 목적에 맞지않음 (시간적 연속성을 반영하지 못하기 때문)

RNN의 출력층 (Dense layer)

• Dense layer
  • RNN의 출력은 주어진 문제에 따라 달라짐
  • 마지막 은닉 상태 $h_T$를 기반으로 결과를 생성함
    
• 완전 연결 계층(fully connected(fc) layer)
  • 결과 값을 출력하는 위치에서 사용, 신경세포(뉴런)의 기능 구현
  • 값이 둘중 하나만 출력된다(0 & 1) == 이진 분류 (binary classification)
  • 값이 여러개로 나온다 (0~1 사이의 값) = 다중 분류
  • $y = w_1x_1 + w_2x_2 + ... + w_nx_n + b$ ($x$는 은닉층의 출력값)
    
    
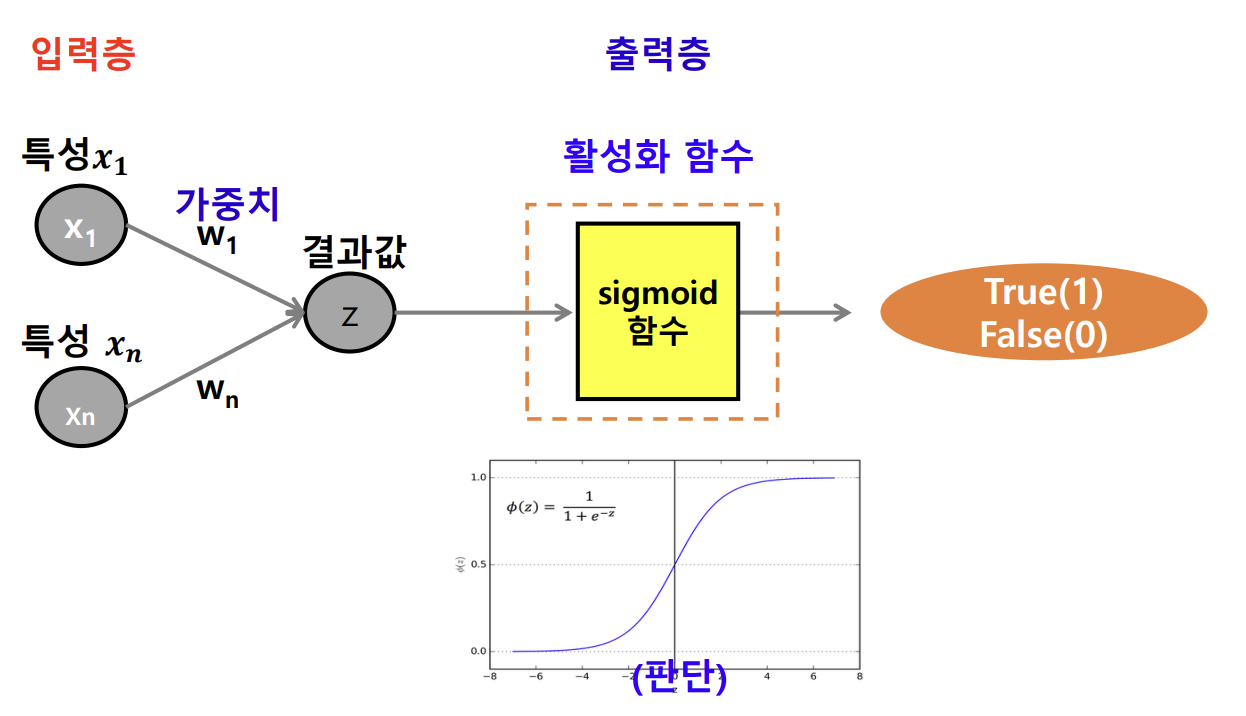
• 활성화 함수 (activation)
  • 입력 값을 출력 값으로 변환하는 함수
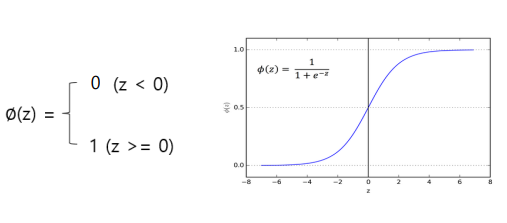
  • 입력의 총합의 결과를 시그모이드 함수의 넣고, 그 결과를 판단하여 출력함
    
  • Sigmoid 함수
    • $z$ == 입력의 총합
    • 값이 0~1사이의 값이 나오게됨
    • 0.5를 기준으로 정답 레이블을 0 과 1로 변환 해줘야 정확한 이진분류가 가능
      

---

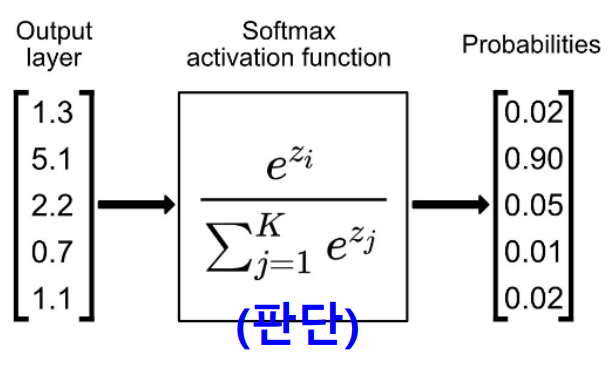
• softmax 함수
  • 이진 분류의 경우
    
  • 다중 분류의 경우
    
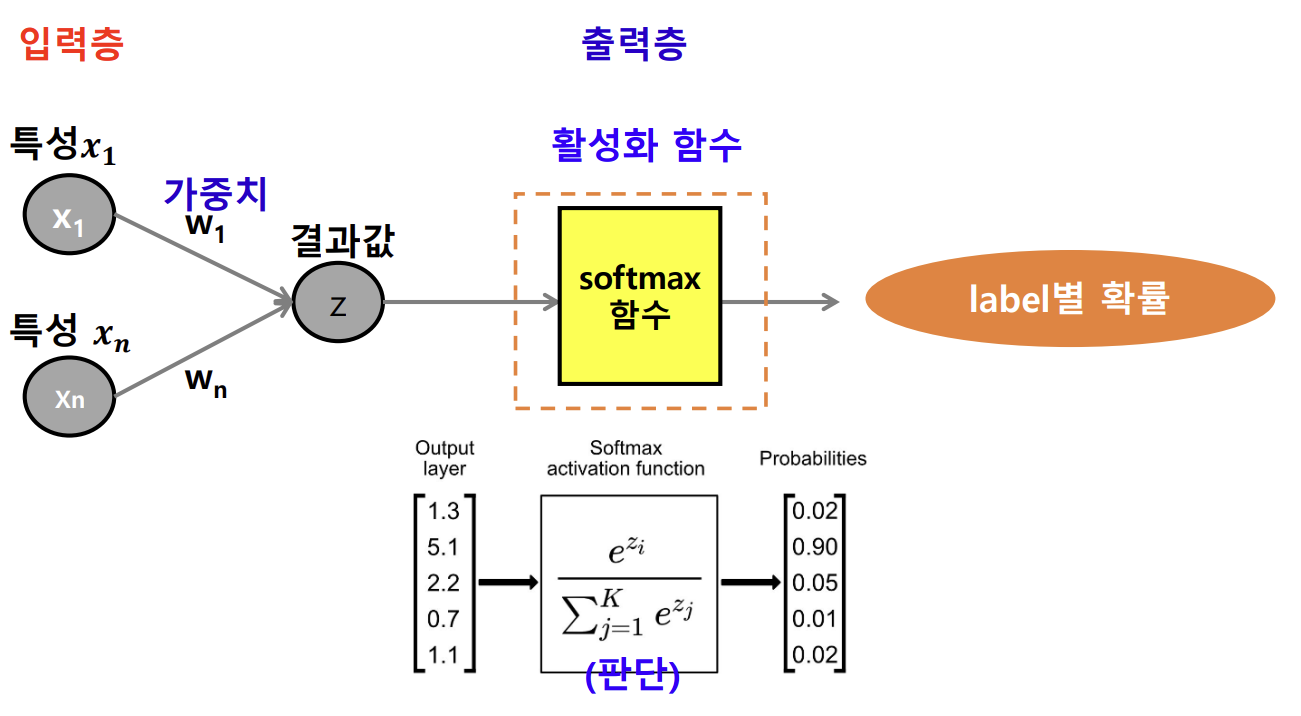
• 다중분류에서 사용되는 활성화 함수
  • 분모 = 입력값의 합, 분자 = 해당 클래스
  • softmax 함수의 출력값은 항상 0과 1사이이며, 모든 출력값의 합은 항상 1임
  • 즉 softmax 함수는 입력값을 확률 분포로 변환하는 함수임
  • 출력층의 각 노드가 특정 클래스에 대한 확률을 나타내며, 예측된 클래스는 확률이 가장 높은 클래스로 예측됨
    • ex) 클래스 1의 확률이 0.7이고 클래스 2의 확률이 0.2라면, 모델은 클래스 1에 속할 가능성이 더 높다고 판단함

Q) RNN dense layer에서 Sigmoid함수의 0~1사이의 값을 다중 분류로 볼 수 있는가?

• 다중 분류는 정답 레이블의 종류가 0&1 등 두 종류가 아닌 것들을 의미함
  
  
• Sigmoid함수의 출력값은 모델이 예측한 값이며, 정답레이블(0 & 1)로 변환 되어 이중 분류를 함

최적화 함수 (optimizer)

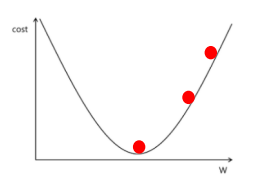
• 기본 : 경사 하강법
  • 수식
    • $W_{new}= W -$ (learning_rate * 현재 가중치에서의 기울기)

---

• 최적화 함수의 종류
  
  
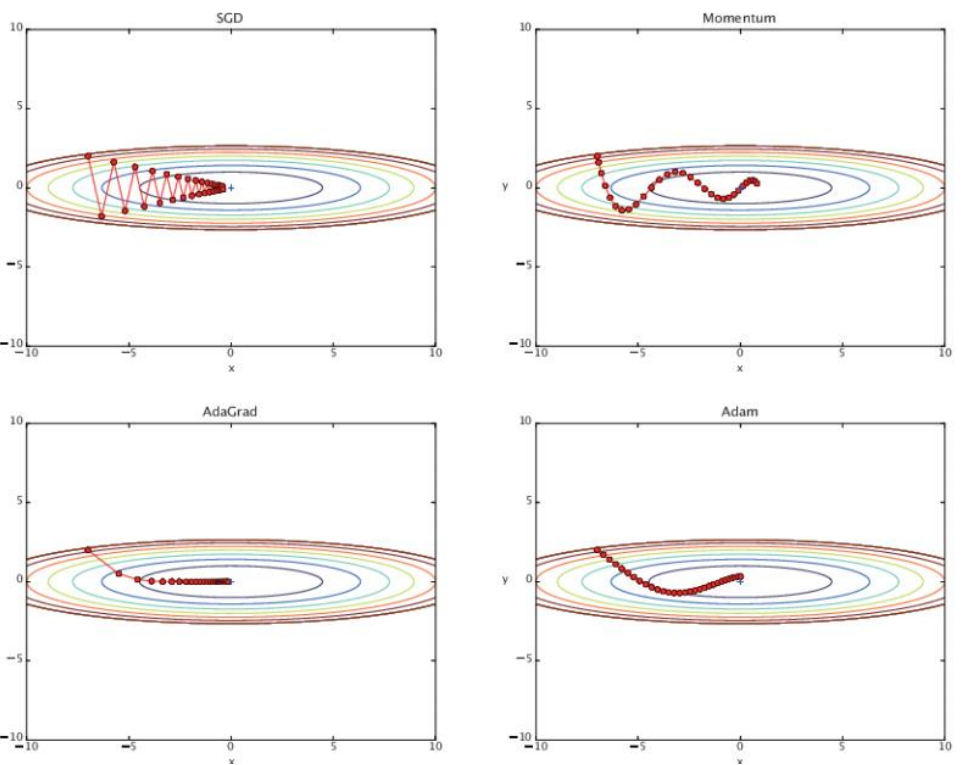
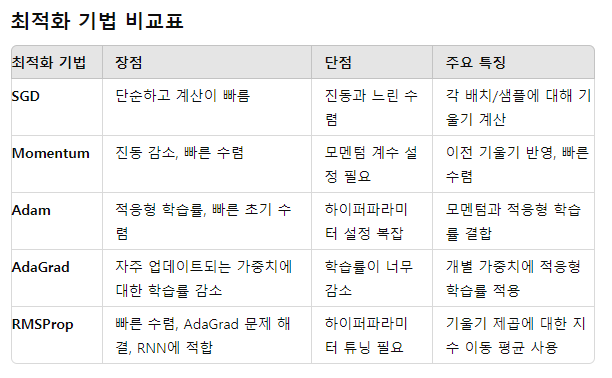
• SGD (Stochastic Gradient Descent)
  • 기본적인 경사 하강법. 전체 데이터 셋이 아니라 랜덤하게 선택한 미니 배치 또는 샘플 하나에 대해 기울기를 계산해 가중치를 업데이트함
    
• Momentum
  • SGD의 단점을 개선. 이전 업데이트 방향을 고려하여 모멘텀(가속도)을 추가하고, 이전 기울기의 일부를 가중치 업데이트에 반영해, 진동을 줄이고 수렴 속도를 높임
    
• AdaGrad (Adaptive Gradient Algorithm)
  • 모든 파라미터에 대해 개별적으로 적응형 학습률을 적용하여, 자주 업데이트되는 파라미터는 학습률을 줄이고, 덜 업데이트되는 파라미터는 학습률을 높이는 방식
    
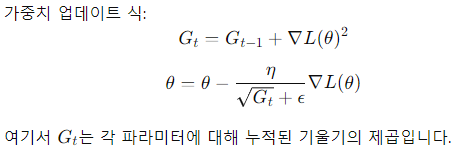
• Adam (Adaptive Moment Estimation)
  • RMSProp(학습률을 각 가중치에 대해 적응적으로 조정)과 Momentum(기울기의 1차 모멘텀과 2차 모멘텀을 모두 사용하는 기법)을 결합한 방법
    
• RMSProp (Root Mean Square Propagation)
  • 기울기의 제곱 이동 평균을 사용해 학습률을 조정함. 학습이 오래된 정보를 덜 반영하고, 새로운 기울기 정보에 더 큰 비중을 둠

+ 역전파

• 신경망 학습에서 모델이 예측한 값과 실제 값 사이의 오차를 계산하고 오차를 통해 가중치를 업데이트하는 방법
  
  
• 경사 하강법과 함께 사용되어 가중치를 점진적으로 업데이트하여 예측 성능을 개선함
  • 순전파 > 오차계산 > 역전파 > 가중치 업데이트 순서로 진행됨
    
    
• 순전파 (Forward Propagation)
  • 입력 데이터를 신경망에 통과 시키면서, 각 층의 가중치를 활용해 계산함 > 출력층에서 예측 결과가 출력됨
  • 오차 계산
    • 모델의 출력과 실제 값(레이블) 사이의 차이를 계산하여 오차를 구함(손실함수 계산)
      
      
• 역전파 (Backpropagation)
  • 계산된 오차를 기반으로 각 가중치에 대해 손실 함수의 기울기를 계산함
  • 출력층부터 시작하여 입력층까지 거꾸로 전달됨
  • 기울기는 신경망의 각 가중치가 손실함수에 얼마나 영향을 미치는지 나타내며, 이를 통해 가중치를 업데이트함
  • 가중치 업데이트
    • 경사 하강법(Gradient Descent)을 사용해, 각 가중치를 손실이 줄어드는 방향으로 조정함

---

(제 지식의 한계로 수식까진 다루지 않겠습니다)