Chapter 2. 마르코프 결정 프로세스

문제를 풀기 위해서는 먼저 문제가 잘 정의되어야 합니다. 강화 학습에서 문제를 잘 정의하려면 주어진 문제를 MDP(Markov Decision Process)의 형태로 만들어야 합니다. 이번 챕터에서는 MDP에 대해 자세히 알아보겠습니다.

---

2.1. 마르코프 프로세스 (Markov Process)

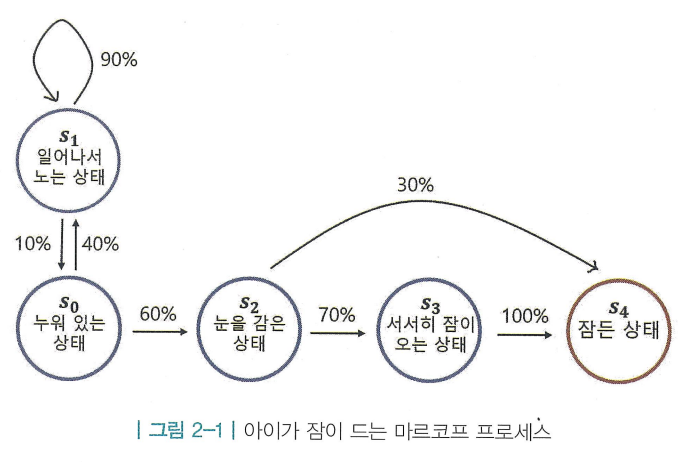
• 마르코프 프로세스 (Markov Process, MP) : 미리 정의된 어떤 확률 분포를 따라서 상태와 상태 사이를 이동하며, 각각에 해당하는 확률이 있고, 그 확를에 따라 다음 상태가 정해지는 프로세스
  • 상태(state) : $s_0$ ~ $s_4$
  • 상태 전이(state transition) : 현재 상태에서 다음 상태로 전이되는 것
  • 종료 상태(terminal state) : 도달하는 순간 마르코프 프로세스가 끝이 나는 상태

$\textbf{MP} \equiv (\mathcal{S}, \mathcal{P})$

• 상태의 집합( $\mathcal{S}$ ) : 가능한 모든 상태들의 집합
• 전이 확률 행렬( $\mathcal{P}$ ) : 전이 확률(transition probability) $\mathcal{P}{ss'}$는 상태s에서 다음 상태 $s'$ 로 전이될 확률
  • $\mathcal{P}{ss'}$를 조건부 확률이라는 개념을 이용해서 다른 방식으로 표현이 가능함
    • $\mathcal{P}{ss'} = \mathbb{P}[S_{t+1} = s' \mid S_t = s]$
    • 시점 $t$ 에서 상태 $s$ 에 있을 때, 다음 시점 $t+1$ 에서 상태 $s'$ 이 될 확률

• 전이 확률 행렬 (Transition Probability Matrix) : 마르코프 프로세스에서 전이 확률 $\mathcal{P}_{ss'}$ 은 모든 상태쌍 $(s, s')$ 에 대해 정의되므로, 이를 행렬 형태로 표현할 수 있기 때문에 전이 확률이 아닌 ‘전이 확률 행렬’이라고 부름
  
  • 상태 공간 $\mathcal{S}$ 의 크기가 $n$ 이라면, $\mathcal{P}$ 는 $n \times n$ 행렬임
  • 전이 확률 행렬의 각 행은 확률 분포이므로, 각 행의 원소 합은 1이 됨

마르코프 성질(Markov Property)

• $\mathbb{P}[s_{t+1} \mid s_t] = \mathbb{P}[s_{t+1} \mid s_1, s_2, \dots, s_t]$
  
  
  • $\mathbb{P}[S_{t+1} = s' \mid S_t = s, S_{t-1} = s_{t-1}, \dots, S_0 = s_0] = \mathbb{P}[S_{t+1} = s' \mid S_t = s]$
  • $\mathbb{P}(S_{t+1} = s' \mid S_t = s) = \mathbb{P}(S_{t+1} = s' \mid S_1, S_2, \dots, S_t = s)$
    
    
• “미래는 오로지 현재에 의해 결정된다”
  • 마르코프 프로세스의 모든 상태는 마르코프 성질을 따름
  • 현재 상태 $S_t$ 이전에 방문했던 상태들 $S_1, S_2, \dots$ 에 대한 정보는 미래 상태 $S_{t+1}$ 를 결정하는 데에 아무런 영향을 주지 못함
    
    
• 마르코프한 상태 : 과거와 무관하게, 현재 상태만으로 다음 행동(수)을 결정할 수 있는 상태
  
  
• 마르코프 하지 않은 상태 : 현재 상태만으로는 충분하지 않고, 과거 정보(속도, 방향 등)가 추가로 필요해 다음 행동을 결정할 수 없는 상태

---

2.2. 마르코프 리워드 프로세스 (Markov Reward Process, MRP)

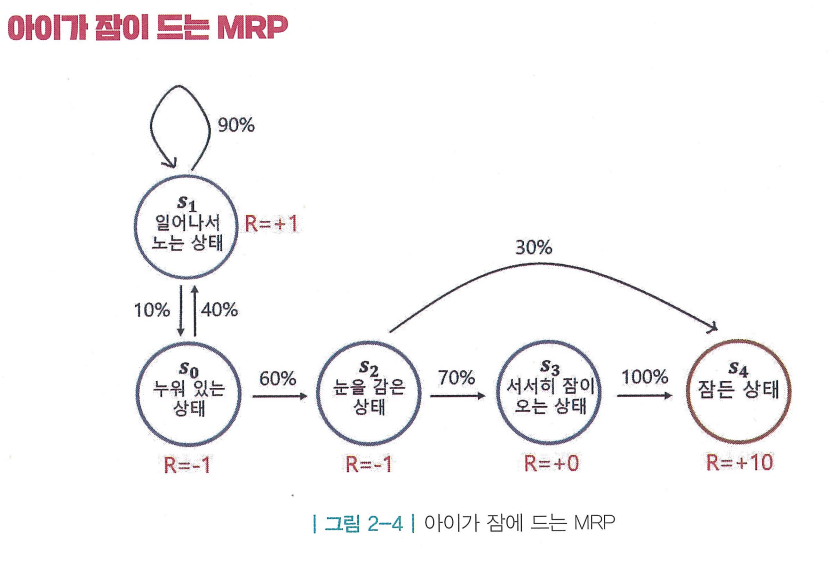
• 마르코프 리워드 프로세스(Markov Reward Process, MRP) : 마르코프 프로세스에 보상의 개념이 추가된 것. 어떤 상태에 도착하게 되면 그에 따른 보상을 받게됨

$\textbf{MRP} \equiv (\mathcal{S}, \mathcal{P}, \mathcal{R}, \gamma)$

• 상태의 집합( $\mathcal{S}$ ) : 가능한 모든 상태들의 집합 (MP의 $\mathcal{S}$ 와 같음)
  
  
• 전이 확률 행렬( $\mathcal{P}$ ) : 상태 s에서 다음 상태 $s'$ 로 전이될 확률을 행렬로 표현 (MP의 $\mathcal{P}$ 와 같음)
  
  
• 보상 함수( $\mathcal{R}$ ) : $\mathcal{R}$ 은 어떤 상태 s에 도착했을 때 받게 되는 보상
  • $\mathcal{R} = \mathbb{E}[R_t \mid S_t = s]$
    • 기대값($\mathbb{E}$ : expectation)이 등장한 이유는 특정 상태에 도달했을 때 받는 보상이 매번 다를 수도 있기 때문에 고정된 값이 필요함
      
      
• 감쇠 인자( $\gamma \in [0, 1]$ ) : $\gamma$(Gamma)는 0에서 1사이의 숫자이며, 강화 학습에서 미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터
  • 미래에 얻을 보상의 값에 $\gamma$가 여러번 곱해지며, 그 값을 작게 만듬

감쇠된 보상의 합, 리턴(Return) : “강화학습은 리턴을 최대화하도록 학습하는 것”

• MRP에서는 MP와 다르게 상태가 바뀔 때마다 해당하는 보상을 얻음
  
  
• 상태 $s_0$에서 보상 $R_0$를 받고 시작하여 종료 상태인 $s_T$에 도착할 때 보상 $R_T$를 받으며 끝이남
  • $s_0, R_0, s_1, R_1, s_2, R_2, \dots, s_T, R_T$ (아래 첨자는 타임 스텝, 즉 시간을 의미함)
    
    
• 에피소드(episode) : 시작 상태 $s_0$에서 부터 종료상태 $s_T$까지의 전체 경로를 의미함
  • 이런 표기법을 이용하여 바로 리턴 $G_t$를 정의하게됨
    
    
  • $G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^\infty \gamma^k R_{t+k+1}$
    
    • 리턴 $G_t$ : 시점 t부터 미래에 받을 감쇠된 보상의 합
    • $\gamma \approx 0$ 이면 단기 보상을, $\gamma \approx 1$ 이면 장기 보상을 중시함
      
      
• 리턴은 과거의 보상을 고려하지 않고 미래의 보상을 통해서 정의된다

$\gamma$가 필요한 이유

• $\gamma$=0일 경우, 미래의 보상이 모두 0이되기 때문에 탐욕적(greedy)인 에이전트가 됨
• $\gamma$=1일 경우, 현재희 보상과 미래의 보상이 완전히 대등하기 때문에 장기적인 시야를 가진 에이전트가 됨

• 수학적 편리성 : $\gamma < 1$ 이기 때문에 MRP를 무한한 스텝동안 진행하더라도 $G_t$ 가 무한한 값이 될 수 없음
  
  
• 사람의 선호 반영: 가까운 시점의 보상에 더 높은 가치를 부여
  
  
• 미래에 대한 불확실성 반영: 시간이 지날수록 다양한 확률적 요소들에 의해 예측이 어려워지는 리스크를 반영

에피소드의 샘플링

• 하나의 에피소드 안에서 방문하는 상태들은 매번 다름. 즉 매번 에피소드가 어떻게 샘플링(sampling)되는 지에 따라 리턴이 달라지게 됨
  
  
• 샘플링 : 어떤 확률 분포가 존재할 때 해당 분포에서 샘플을 뽑아보는 것
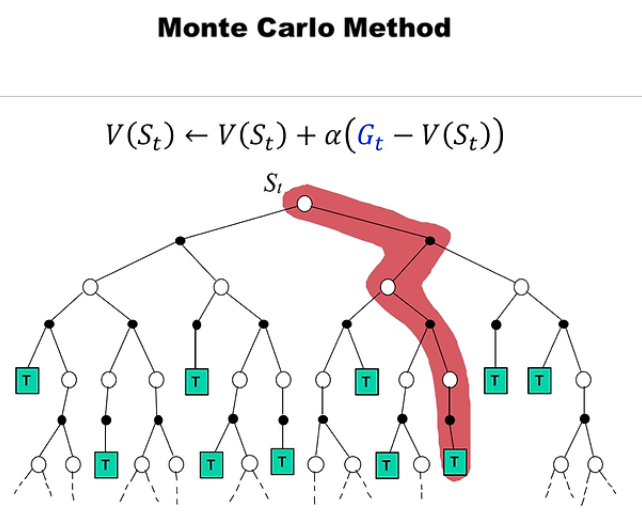
  • 많은 경우 실제 확률 분포를 잘 모르는 경우가 대부분이기 때문에 샘플링을 통해서 어떤 값을 유추하는 방법론을 사용함 > Monte-Carlo 접근법

상태 가치 함수(State Value Function)

• MRP의 목표는 특정 상태 s의 밸류(value)혹은 가치를 평가하는 것. 이는 상태 s에서 시작했을 때 받을 리턴의 기댓값으로 측정할 수 있음
  
  
• 상태 가치 함수(v(s)) : 상태를 인풋으로 넣으면 그 상태의 밸류를 아웃풋으로 출력하는 함수. 에피소드마다 리턴이 다르기 때문에 어떤 상태 s의 밸류 v(s)는 기댓값을 이용하여 정의함
  
  
• $v(s) = \mathbb{E}[G_t \mid S_t = s]$ : 상태 s로부터 시작하여 얻는 리턴의 기댓값
  • 시점 t에서 상태 s부터 시작하여 에피소드가 끝날 때까지의 리턴을 계산함

---

2.3 마르코프 결정 프로세스 (Markov Decision Process, MDP)

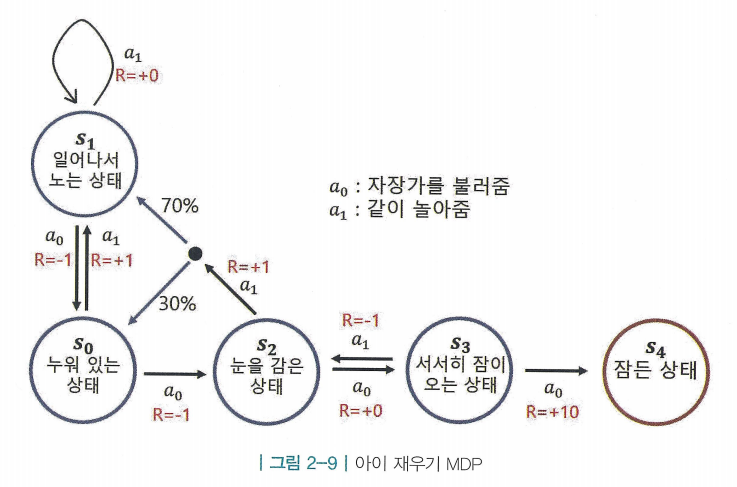
• MP와 MRP에 경우 상태 변화가 자동으로 이루어짐. 즉, 순차적 의사결정 문제를 모델링 할 수 없음
  
  
• 마르코프 결정 프로세스 (Markov Decision Process, MDP) : 순차적 의사결정 문제의 핵심인 의사결정(decision)을 모델에 포함 시키기 위해, 자신의 의사를 가지고 행동하는 주체인 에이전트를 포함함
  
  
• MDP를 정의하기 위해 액션의 집합 A를 추가함. A가 추가되면서 기존의 P, R의 정의도 MRP와 달라짐
  
  
• 상태(s)는 환경의 일부이며, 에이전트가 조절할 수 없음. 즉, 확률 값을 바꿀 수는 없음

$\textbf{MDP} \equiv (\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma)$

• 상태의 집합( $\mathcal{S}$ ) : 가능한 모든 상태들의 집합 (MP와 MRP의 $\mathcal{S}$ 와 같음)
  
  
• 액션의 집합($\mathcal{A}$ ) : 에이전트가 취할 수 있는 액션들을 모아놓은 것. 에이전트는 스템마다 액션의 집합 중에서 하나를 선택함
  
  
• 전이 확률 행렬( $\mathcal{P}$ ) : 전이 확률 $P^a_{ss'}$는 현재 상태가 s이며 에이전트가 액션 a를 선택했을 때 다음 상태가 $s'$ 이 될 확률
  • 주의) 같은 상태 s에서 같은 액션 a를 선택해도 매번 다른 상태에 도착할 수 있음. 즉, 액션 실행 후 도달하는 상태 $s'$ 에 대한 확률 분포가 있고 그것이 전이 확률 행렬( $\mathcal{P}$ )임
  • $\mathcal{P}^a_{ss'} = \mathbb{P}[S_{t+1} = s' \mid S_t = s, A_t = a]$
    • 조건 : 현재 상태 s에서, 액션 a를 했을때
      
      
• 보상 함수( $\mathcal{R}$ ) : $\mathcal{R}^a_s$는 상태 s에서 액션 a를 선택하면 받게 되는 보상
  • 현재 상태 s에서 어떤 액션을 선택하느냐에 따라 받는 보상이 달라짐
  • $\mathcal{R}^a_s = \mathbb{E}[R_{t+1} \mid S_t = s, A_t = a]$
    • 받는 보상은 확률적으로 매번 바뀔 수 있기 때문에 기대값을 이용하여 표기함
      
      
• 감쇠 인자( $\gamma$) : 미래에 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터 (MRP의 $\gamma$와 같음)

정책 함수와 2가지 가치 함수

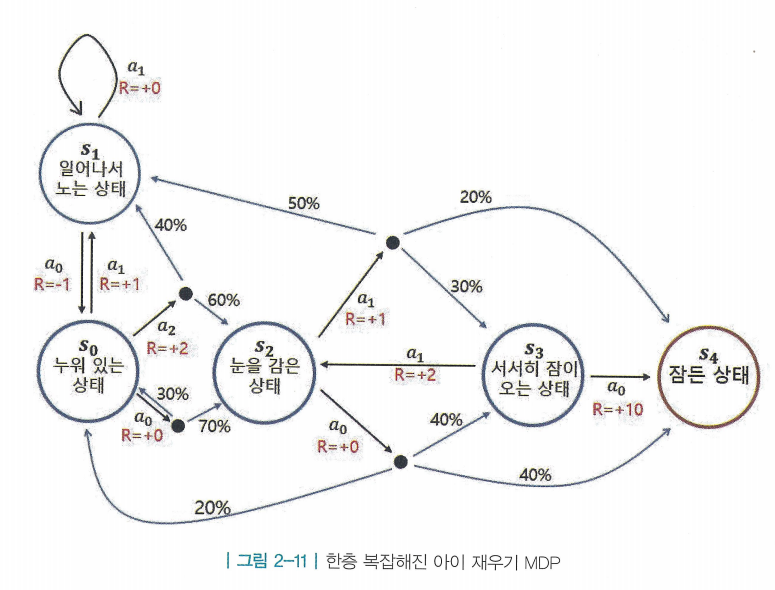
• MDP가 복잡해지면 최적 행동을 찾는 것이 어려워짐. 핵심은 “각 상태 s에 따라 어떤 액션 a를 선택해야 보상의 합을 최대로 할 수 있는가” > 이를 정책(policy)라고 함

• 정책 혹은 정책 함수(Policy Function) ( $\pi$ ) : 각 상태에서 어떤 액션을 선택할지 정해주는 함수. 에이전트의 목적은 보상의 합을 최대화하는 정책을 찾는것임
  • $\pi(a \mid s) = \mathbb{P}(A_t = a \mid S_t = s)$ : 정책 함수를 확률을 이용하여 정의
    • 상태 s에서 액션 a를 선택할 확률
    • (이를 확률적 정책이라 하며, 결정론적 정책은 $\pi(s) = a$로 정의한다)
      
      
  • 각 상태에서 할 수 있는 모든 액션의 확률 값을 더하면 1이 되어야 함
    
    
  • 주의) 정책 함수는 에이전트 안에 존재함. 즉, 환경에 대한 그림에선 정책에 대한 내용(상태별 액션을 얼마큼의 확률로 고를지에 대한 내용)이 포함 되지 않음
    
    
• 환경은 변하지 않지만 에이전트는 자신의 정핵을 언제든 수정할 수 있으며, 더 큰 보상을 얻기 위해 계속해서 정책을 교정해 나가는 것이 곧 강화학습임

• MDP에서의 상태 가치 함수 : 에이전트의 정책 함수에 따라서 얻는 리턴이 달라지기 때문에 가치 함수는 정책 함수에 의존적임
  • 가치 함수를 정의하기 위해서는 먼저 정책 함수 $\pi$ 가 정의되어야 함
    
    
  • $v_\pi(s) = \mathbb{E}_{\pi} \left[ r{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots \mid S_t = s \right] = \mathbb{E}_{\pi} \left[ G_t \mid S_t = s \right]$
    • ($\pi$ 가 주어졌다고 가정 했을 때 가치 함수의 정의)
    • s부터 끝까지 $\pi$ 를 따라서 움직일 때 얻는 리턴의 기대값

• 상태-액션 가치 함수(State-Action Value Function) ( $q_\pi(s, a)$ ): 어떤 상태에서 특정 행동을 했을 때 앞으로 얼마나 보상을 받을지를 나타내는 함수
  • 상태에 따라 액션의 결과가 달라지기 때문에 함수에 상태와 액션이 동시에 인풋으로 들어감.
    • s에서 a를 선택하는 것의 밸류가 나옴. a를 선택하고 나면 상태를 진행하기 위해 액션을 선택해야 하는데 그 역할을 정책 함수 $\pi$ 에게 맡김
      
      
  • 상태-액션 가치 함수는 상태와 액션의 페어, 즉 (s, a)를 평가하는 함수임
    
    
  • $q_\pi(s, a) = \mathbb{E}_\pi [ G_t \mid S_t = s, A_t = a ]$
    • ( $v_\pi(s)$와 동일하게 미래에 얻을 리턴 $G_t$를 통해 밸류를 측정하며, 정책 $\pi$ 에 따라 이후의 상태가 달라지므로 $\pi$ 를 고정시키고 평가함)
    • s에서 a를 선택하고, 그 이후에는 $\pi$ 를 따라서 움직일 떄 얻는 리턴의 기댓값

• $v_\pi(s)$와 $q_\pi(s, a)$는 “s에서 어떤 액션을 선택하는가”하는 부분만 차이가 존재함
  • $v_\pi(s)$를 계산할 때는 s에서 $\pi$ 가 액션을 선택함
    
    
  • $q_\pi(s, a)$를 계산할 때는 s에서 강제로 a를 선택함 > 액션을 선택한 이후에는 2가지 가치 함수 모두 정책 함수 $\pi$ 를 따라서 에피소드가 끝날 때까지 진행됨

MP, MRP, MDP 요약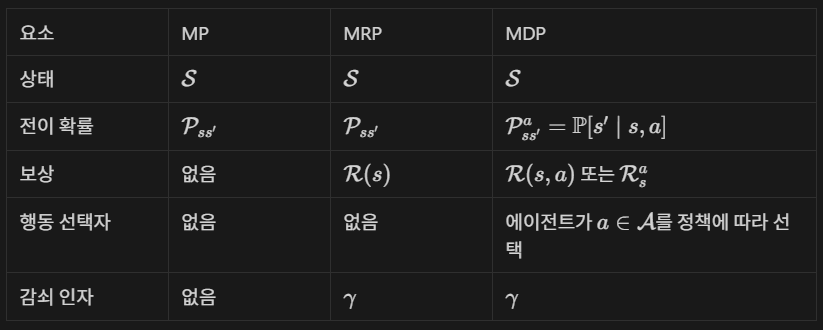

---

2.4 Prediction과 Control

• 큰 흐름에서 강화 학습은 문제와 솔루션으로 나눌 수 있고, 문제의 세팅이라 함은 주어진 상황이 있을 때 이를 MDP의 형태로 만들어서, MDP를 풀고자 하는 것임
  • MDP가 주어 졌을때, 즉 $(\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma)$이 주어졌을 때 task는 크게 Prediction과 Control로 볼 수 있음

1. Prediction: 정책 $\pi$ 가 주어졌을 때, 각 상태의 값을 평가하는 문제

2. Control: 최적의 정책(optimal policy) $\pi^*$ 를 찾는 문제

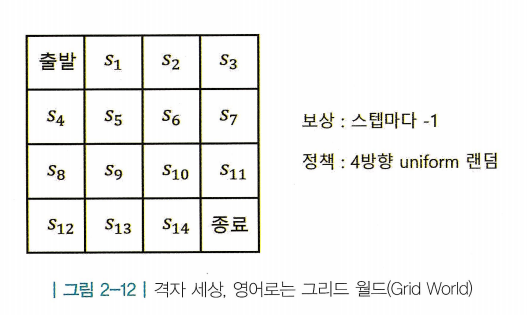
• Prediction : 특정 상태 s의 밸류 $v_\pi(s)$의 값을 구하는 문제. 즉, 해당 상태의 백류를 예측하는것이 목표

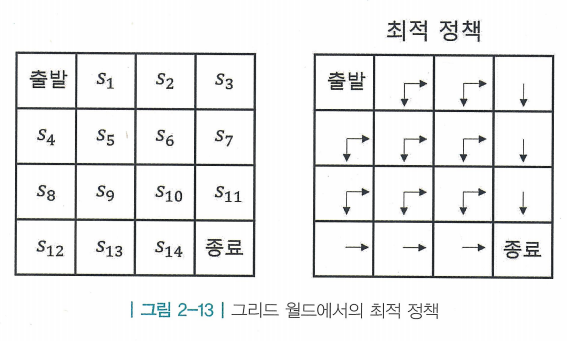
• Control : 최적의 정책 $\pi^*$ 를 찾는 것이 목표. 최적의 정책이란 이 세상에 존재하는 모든 $\pi$중에서 가장 기대 리턴이 큰 $\pi$를 뜻함
  • 최적 정책 $\pi^*$ 를 따를 때의 가치 함수를 최적 가치 함수(optimal calue function)이라고 하며 $v^*$ 로 표기함
  • $\pi^*$ 와 $v^*$ 를 찾았다면 “이 MDP는 풀렸다”라고 함.

"강화 학습을 이용해 실생활의 어떤 문제를 MDP 형태로 만들고, 그 MDP의 최적 정책과 최적 가치 함수를 찾아내어 MDP를 푸는 것이 목적이다"