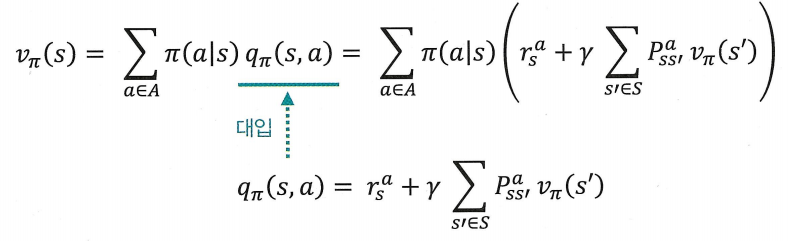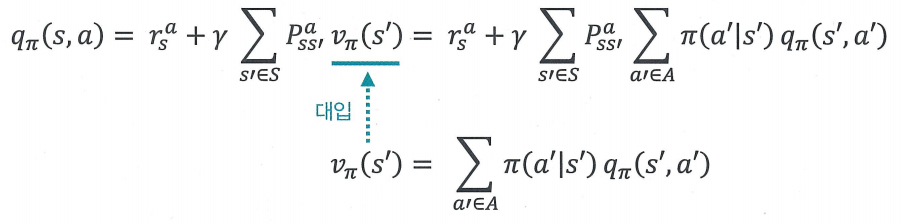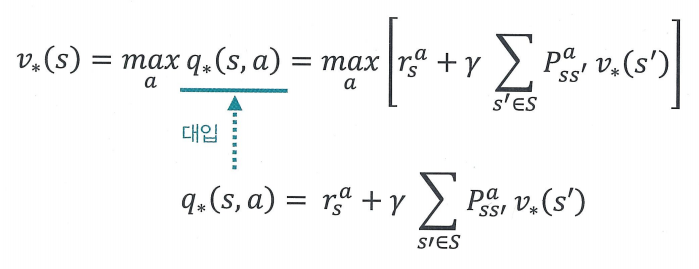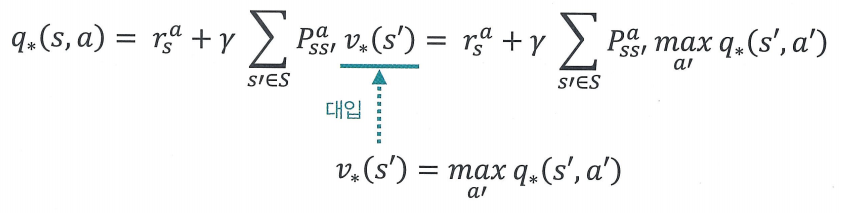대부분의 강화 학습 알고리즘은 밸류를 구하는 것에서 출발합니다. 그리고 밸류를 구하는 데 뼈대가 되는 수식이 바로 벨만 방정식입니다. 벨만 기대 방정식과 벨만 최적 방정식이라는 두 종류의 방정식을 배워봅니다.
재귀함수
- 벨만 방정식은 기본적으로 재귀적 관계에 대한 식임
- 시점 t에서의 밸류와 시점 t+1에서의 밸류 사이의 관계를 다루며, 또한 가치함수와 정책 함수 사이의 관계도 다룸
- 재귀 함수 : 자기 자신을 호출하는 함수 (ex - 피보나치 수열)
- 피보나치 수열 일반화
- fib(n)=51((21+5)n−(21−5)n)
- 재귀함수를 이용한 표현
- fib(n)=fib(n−1)+fib(n−2)
3.1 벨만 기대 방정식 (Bellman Expectation Equation)
- 0단계
vπ(st)=Eπ[rt+1+γvπ(st+1)]
qπ(st,at)=Eπ[rt+1+γqπ(st+1,at+1)]
- 1단계
vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)
qπ(s,a)=rsa+γ∑s′∈SPss′avπ(s′)
- 2단계
vπ(s)=∑a∈Aπ(a∣s)(rsa+γ∑s′∈SPss′avπ(s′))
qπ(s,a)=rsa+γ∑s′∈SPss′a∑a′∈Aπ(a′∣s′)qπ(s′,a′)
0단계
vπ(st)=Eπ[rt+1+γvπ(st+1)]
1단계
vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)
- 액션 밸류 qπ(s,a)를 이용하여 상태 밸류 vπ(s)를 표현
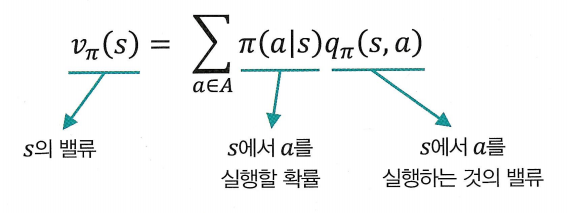
- 즉, 어떤 상태에서 선택할 수 있는 모든 액션의 밸류를 모두 알고 있다면, 이를 이용해 해당 상태의 밸류를 계산할 수 있음
- qπ(s,a)에 액션을 선택할 확률을 곱하고, 모두 더해주는 방식임
qπ(s,a)=rsa+γ∑s′∈SPss′avπ(s′)
- 상태 밸류 vπ(s)를 이용하여 액션 밸류 qπ(s,a)를 표현
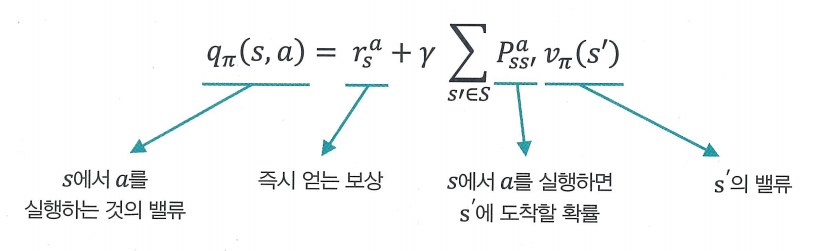
- s에서 a를 실행하는 것의 밸류를 표현하기 위해선 아래 3가지 정보를 모두 알고있어야함
- a를 선택하자 마자 얻는 보상의 값
- a를 선택했을 경우 다음 상태가 어디가 될지 그 각각에 대한 전이 확률
- 각 상태의 밸류 v(s1) (t=1,2,3,…)
2단계
vπ(s)=∑a∈Aπ(a∣s)(rsa+γ∑s′∈SPss′avπ(s′))
- 1단계의 qπ에 대한 식을 vπ에 대한 식에 대입
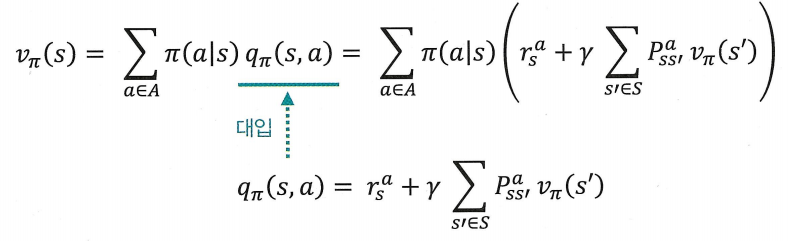
qπ(s,a)=rsa+γ∑s′∈SPss′a∑a′∈Aπ(a′∣s′)qπ(s′,a′)
- 1단계의 vπ에 대한 식을 qπ에 대한 식에 대입
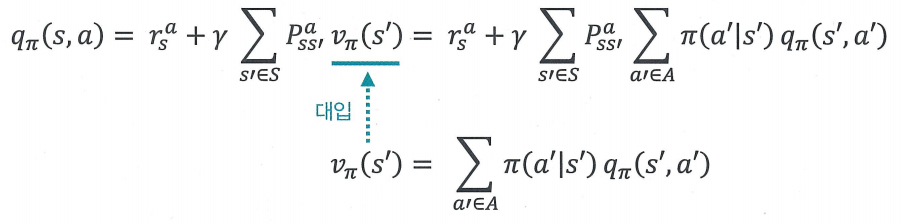
0단계 : vπ(st)=Eπ[rt+1+γvπ(st+1)]
2단계 : vπ(s)=∑a∈Aπ(a∣s)(rsa+γ∑s′∈SPss′avπ(s′))
- st를 s로, st+1을 s′으로 표기법을 통일하고 보면, 0단계와 2단계 모두 vπ(s)에 대한 식임
-
0단계 : 현재 상태의 밸류와 다음 상태의 밸류를 기댓값 연산자를 통해 연결해 놓은 식
-
2단계 : 0단계에서 그 기댓값을 계산하기 위한 식
- 즉, 수식도 결국 현재 상태의 밸류와 다음 상태의 밸류 사이 연결고리를 나타내며, 0단계에 있는 기댓값 연산자를 모든 확률과 밸류의 곱 형태로 풀어서 쓴 형태
- 2단계 식을 계산하기 위해서는 다음 2가지를 반드시 알아야함
- 보상 함수 rsa : 각 상태에서 액션을 선택하면 얻는 보상
- 전이 확률 pss′a : 각 상태에서 액션을 선택하면 다음 상태가 어디가 될지에 관한 확률 분포
-
여기서 rsa과 pss′a는 환경의 일부임. 이 2가지에 대한 정보를 알 때 “MDP를 안다” 고 표현
- rsa를 안다는 것 : 상태 s에서 액션 a를 해보기도 전에 얼마의 보상을 받을지 그 기댓값을 안다는 것
- pss′a를 안다는 것 : 상태 s에서 액션 a를 했을 때 어떤 상태에 도달하게 될지 그 확률 분포를 미리 다 알고 있다는 것
-
실제 세계에는 MDP에 대한 모든 정보를 아는 상황보다 모르는 상황이 더 많음
- 미리 rsa를 알지 못하기 때문에 실제로 상태 s에서 액션 a를 해보는 수밖에 없음
- 이후, 시행했을 때 받는 보상 등의 경험을 통해 학습하게됨
-
이렇게 MDP에 대한 정보를 모를 때 학습하는 접근법을 “모델-프리(model-free)” 접근법이라고 함
- 반대로, rsa와 pss′a를 다 안다면 실제로 경험해보지 않고 머릿속에서 시뮬레이션 해보는 것도 가능한데, 이런 종류의 접근법을 “모델 기반(Model-based)” 혹은 “플래닝(planning)” 이라고함
3.2 벨만 최적 방정식 (Bellman Optimality Equation)
최적 벨류와 최적 정책
- 벨만 기대 방정식 : vπ(s)와 qπ(s,a)에 대한 수식
- vπ(s)와 qπ(s,a)는 모두 정책이 π로 고정되었을 때의 밸류에 관한 함수
- 벨만 최적 방정식 : v∗(s)와 q∗(s,a)에 대한 수식
- v∗(s)와 q∗(s,a)는 최적 밸류(value)에 대한 함수
v∗(s)=maxπvπ(s)
q∗(s,a)=maxπqπ(s,a)
- 어떤 MDP가 주어졌을 때 그 MDP 안에 존재하는 모든π 들 중에서 가장 좋은 π를 (vπ(s)의 값을 가장 높게 하는 선택) 하여 계산한 밸류가 곧 최적 밸류 v∗(s)라는 뜻
- 실제로 모든 상태에서, 모든 상태에서 최적 밸류를 갖게 하는 정책 π∗가 최소한 1개 이상 존재함
- 이 정책 π∗를 따르면 모든 상태에 대해 그 어떤 정책보다도 높은 밸류를 얻게 됩니다. 이러한 정책 π∗를 최적 정책(optimal policy) 이라고함
- 즉, 최적 정책은 모든 정책 π1,π2,π3,...,π∞ 중에 제일 좋은 정책
- 쉬운 버전 설명
- 다른 정책을 따를 때보다 최적의 정책 π∗를 따를 때 얻는 보상의 총 합이 가장 크다
- 어려운 버전 설명
- “모든 상태 s에 대해, vπ1(s)>vπ2(s) 이면 π1>π2이다.”
- 만약 존재하는 모든 상태에 대해서π1의 밸류가 π2의 밸류보다 크다면 π1이 더 좋다고 표현 가능함. 즉, 정책 사이의 더 좋다는 기호를 ‘>’를 사용하여 표현하면 π1>π2가 성립하는 것
- 부분 순서(partial ordering) : 전체 중에 일부만 대소관계를 비교하여 순서를 정할 수 있다는 뜻
- 세상에 존재하는 모든 정책들 사이 서열을 매길 수는 없지만, 그중에는 서열을 매길 수 있는 정책들이 부분적으로 존재함
- 즉, “MDP 내의 모든 π에 대해 π∗ > π 를 만족하는 π∗가 반드시 존재한다.”
- 최적의 정책만 정의되고 나면 최적 밸류, 최적의 액션 밸류는 다음과 같은 등식이 성립함.
- 최적의 정책: π∗
- 최적의 밸류: v∗(s)=vπ∗(s) (π∗를 따랐을 때의 밸류)
- 최적의 액션 밸류: q∗(s,a)=qπ∗(s,a) (π∗를 따랐을 때의 액션 밸류)
벨만 최적 방정식
- 0단계
v∗(st)=maxaE[rt+1+γv∗(st+1)]
q∗(st,at)=E[rt+1+γmaxa′q∗(st+1,a′)]
- 1단계
v∗(s)=maxaq∗(s,a)
q∗(s,a)=rsa+γ∑s′∈SPss′av∗(s′)
- 2단계
v∗(s)=maxa[rsa+γ∑s′∈SPss′av∗(s′)]
q∗(s,a)=rsa+γ∑s′∈SPss′amaxa′q∗(s′,a′)
- 벨만 최적 방정식에서는 π에 의한 확률적 요소가 사라짐. 액션을 선택할 때 확률적으로 선택하는 것이 아니라 최댓값(max) 연산자를 통해 제일 좋은 액션을 선택하기 때문.
0단계
v∗(st)=maxaE[rt+1+γv∗(st+1)]
q∗(st,at)=E[rt+1+γmaxa′q∗(st+1,a′)]
-
상태 s에서의 최적 밸류는 일단 한 스텝만큼 진행하여 보상을 받고, 다음 상태인 s′의 최적 밸류를 더하는 것으로 벨만 기대 방정식 0단계 수식과 동일하지만, Eπ가 E로 바뀜
- 벨만 기대 방정식에서는 주어진 π가 액션을 선택했지만, 벨만 최적 방정식에서는 할 수 있는 모든 액션들 중에 E[r+γv∗(s′)]의 값을 가장 크게 하는 액션 a를 선택해야 하기 때문에 π의 역할은 없어져 사라짐
- 하지만, 환경에 의한 확률적 요소가 남아있어, 전이 확률에 의해 다양한 s′에 도달할 수 있고 그때마다 r+γv(s′)의 값이 달라지기 때문에 여전히 기댓값 연산자가 필요함
-
(q∗(s,a)에 대한 식은 이후에 Q러닝에 대한 내용을 배울 때 다시 등장)
1단계
v∗(s)=maxaq∗(s,a)
- 상태 s의 최적 밸류는 s에서 선택할 수 있는 액션들 중에 밸류가 가장 높은 액션의 밸류와 같다는 뜻
- 벨만 최적 방정식에서는 100%의 확률로 최적의 밸류를 선택하기 때문에 각 액션을 선택할 확률의 대한 변수가 제거됨
q∗(s,a)=rsa+γ∑s′∈SPss′av∗(s′)
- 벨만 기대 방정식 1단계 수식과 동일 (q(s,a),v(s′)이 q∗(s,a),v∗(s′)로 변경)
2단계
v∗(s)=maxa[rsa+γ∑s′∈SPss′av∗(s′)]
- v∗(s)의 식에 q∗(s,a)의 식 대입
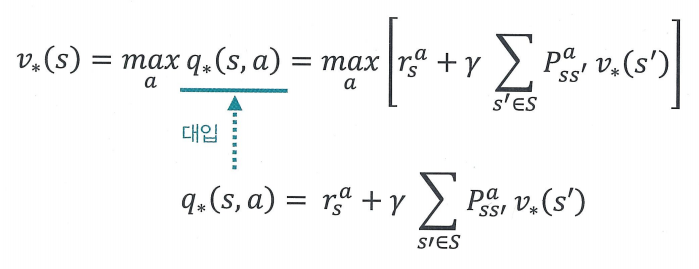
- 현재 상태의 최적 밸류와 다음 상태의 최적 밸류 사이 관계 식을 얻음. 이를 통해 MDP를 알때 최적 밸류를 구할 수 있음
q∗(s,a)=rsa+γ∑s′∈SPss′amaxa′q∗(s′,a′)
- q∗(s,a)의 식에 v∗(s)의 식 대입
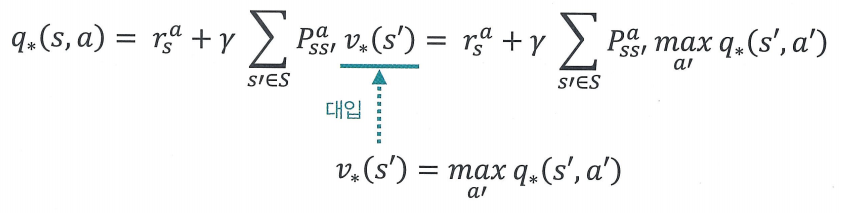
정리
- 벨만 기대 방정식 : 무언가 정책 π가 주어져 있고, 룰을 평가하고 싶을 때
- 벨만 최적 방정식 : 최적의 밸류를 찾는 일을 할 때