벨만 방정식 학습으로 간단한 MDP를 풀 수 있습니다. 벨만 방정식을 반복적으로 적용하는 방법론을 통해 아주 간단한 MDP를 직접 풀어봅니다.
- 작은문제 : MDP에서 상태 집합 S나 액션의 집합 A의 크기가 작은 경우
- MDP를 알 때 : 보상 함수와 전이 확률 행렬을 알고있는 것
- 플래닝(planning) : MDP에 대한 모든 정보를 알 때, 이를 이용하여 정책을 개선해 나가는 과정
- 즉, 미래가 어떤 과정을 거쳐 정해지는지 알고있는 상황에서 시뮬레이션 하며 계획을 세우는 것
- 즉, 미래가 어떤 과정을 거쳐 정해지는지 알고있는 상황에서 시뮬레이션 하며 계획을 세우는 것
- 테이블 기반 방법론(tabular method) : 모든 상태 혹은 상태와 액션의 페어 에 대한 테이블을 만들어서 값을 기록해 놓고, 그 값을 조금씩 업데이트하는 방식
- 상태나 액션의 개수가 많지 않아 그에 해당하는 테이블을 만들 수 있어서 가능한 방법론
4.1 밸류 평가하기 - 반복적 정책 평가 
- 4방향 랜덤이라는 정책 함수 가 주어졌고 이때 각 상태 s에 대한 가치 함수 를 구하는 전형적인 prediction 문제
- 반복적 정책 평가(iterative policy evaluation) : 테이블의 값들을 초기화한 후, 벨만 기대 방정식을 반복적으로 사용하여 테이블에 적어 놓은 값을 조금씩 업데이트해 나가는 방법론
- MDP에 대한 모든 정보를 알 때 사용
1. 테이블 초기화 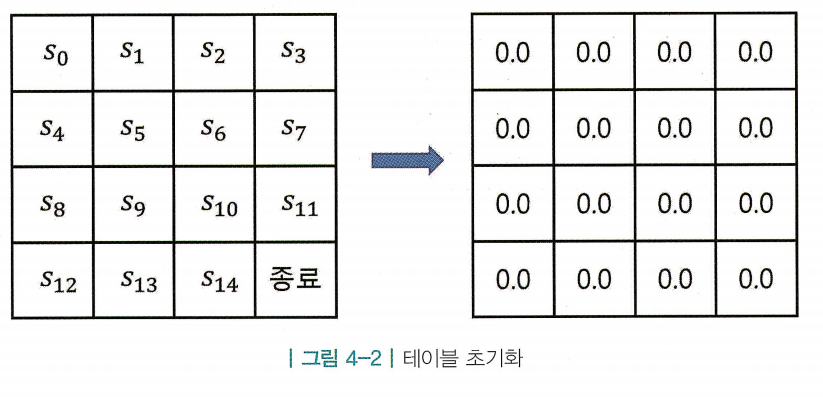
- 테이블에 상태별 밸류 를 기록하기 때문에 테이블의 빈칸은 MDP 안의 상태 s의 개수만큼 필요함 (그림 4-2기준 16개)
- 어떤 값으로 초기화해도 상관없지만, 정답과 멀수록 업데이트 횟수가 더 많이 필요함 (정답을 모르는 경우 적당한 값인 0으로 초기화)
2. 한 상태의 값을 업데이트 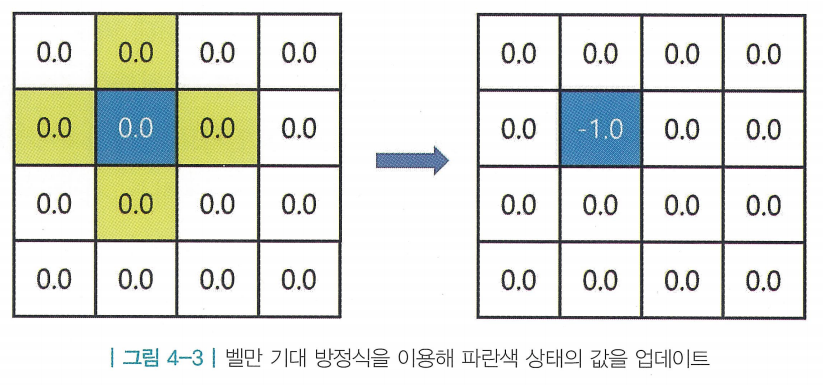
- 가 업데이트를 진행하는 상황
- MDP를 알기 때문에 노란색 상태가 후보가 됨
- MDP를 알기 때문에 노란색 상태가 후보가 됨
- 현재상태와 다음 상태의 밸류 사이 관계식 : 벨만 기대 방정식
-
- 그림 4-3에서의 계산식 :
-
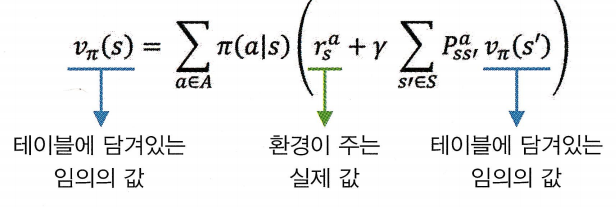
- 현재 테이블에 담겨 있는 값은 마음대로 정한 무의미한 값이지만, 이를 다음 상태의 값과 보상이라는 실제 환경이 주는 정확한 값을 섞어서 업데이트 하기 때문에 조금씩 정확한 값에 다가가게됨
3. 모든 상태에 대해 2 의 과정을 적용 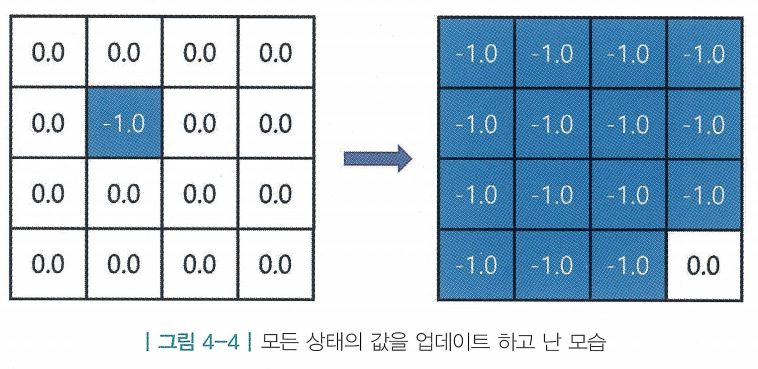
- 앞서 상태의 값을 업데이트하고, 같은 방법으로 마지막 상태를 제외한 모든 상태를 업데이트함
4. 앞의 2 ~ 3 과정을 계속해서 반복 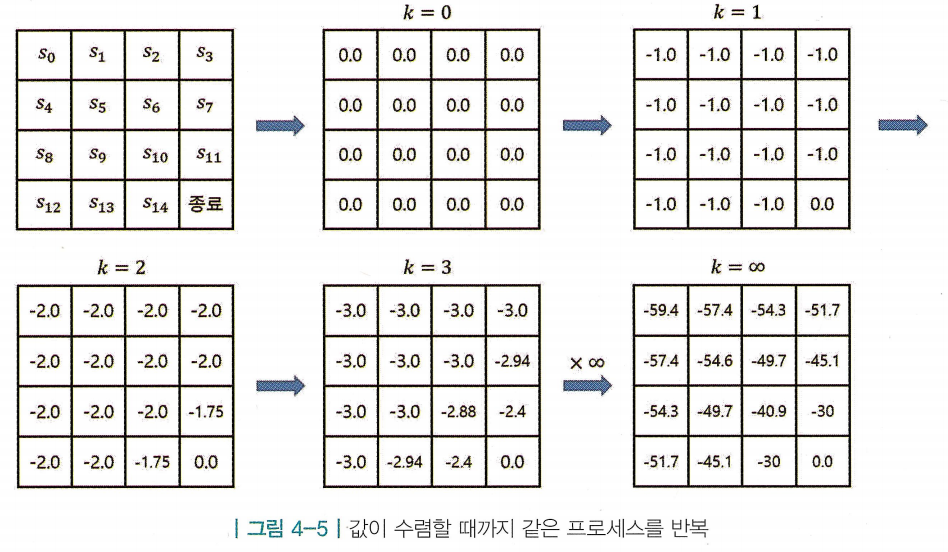
- 한 번 테이블의 모든 값을 업데이트하는 과정을 여러 번 반복 (반복 횟수는 k로 표시)
- 과정을 반복하면 어떤 값에 수렴함 > 그 값이 해당 상태의 실제 밸류임
4.2 최고의 정책 찾기 - 정책 이터레이션
- MDP를 알때 최적 정책을 찾는 2가지 방법 : 정책 이터레이션, 밸류 이터레이션
- 정책 이터레이션 : 기본적으로 정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때까지 반복하는 방법론
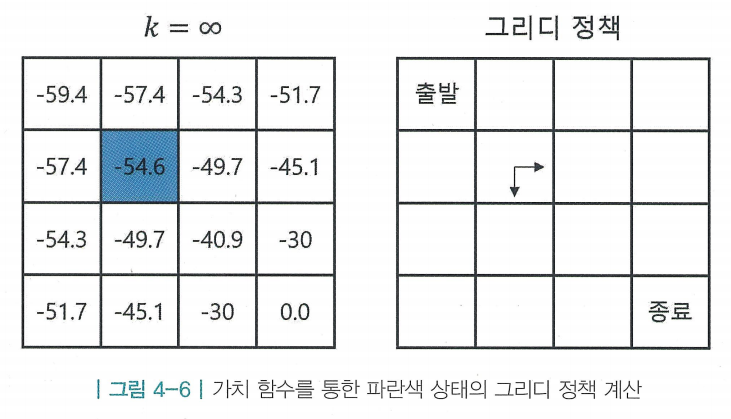
- 기준으로 밸류가 더 큰 상태로 이동하는 것이 좋은 액션임 (즉, 동쪽과 남쪽)
- 여기서 는 원래 정책 보다 나은 정책이며, 이를 그리디 정책(greedy policy)라고 함
- 여기서 는 원래 정책 보다 나은 정책이며, 이를 그리디 정책(greedy policy)라고 함
- 주어진 랜덤 정책 에 대해 밸류를 평가하고, 그에 대해 greedy한 정책을 표시하면, 그 정책이 곧 최적 정책과 일치함
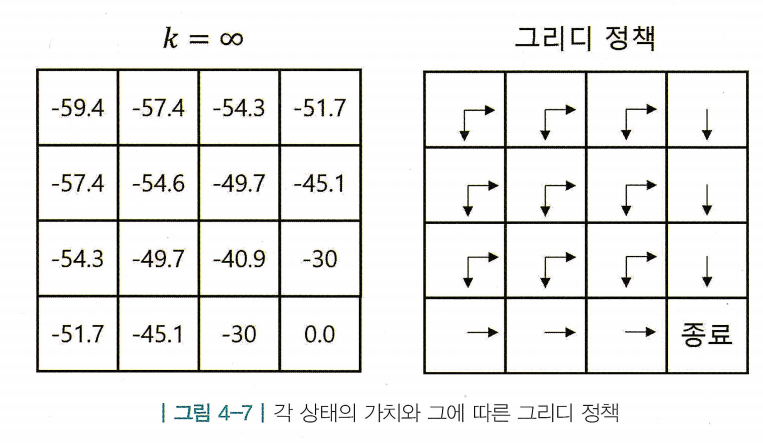
- 뿐만 아니라 모든 상태에 대해 그리디 정책을 표시한 결과
- 이 에 비해 개선되는 점이 “정책 이터레이션(policy iteration)”의 핵심
평가와 개선의 반복 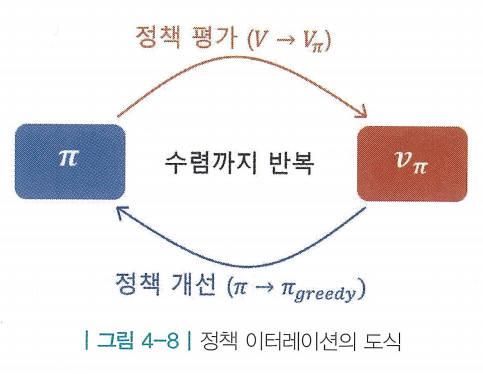
- 정책 이터레이션은 총 2단계로 이루어져 있음
- 처음에는 정책 를 임의의 정책으로 초기화해놓고 시작함
- 정책 평가(policy evaluation) : 를 따랐을 때 각 상태의 가치를 평가하는 일
- 반복적 정책 평가를 사용하여 테이블에 각 상태의 밸류를 채워넣음
- 반복적 정책 평가를 사용하여 테이블에 각 상태의 밸류를 채워넣음
- 정책 개선(policy improvement) : 앞서 정책 평가 단계에서 구한 를 이용해 에 대한 그리디 정책을 만들어 새로운 정책 를 생성함
- 를 생성하면 이 보다 좋은 정책이기 때문에, 즉 가 성립하기 때문에 정책의 개선이 발생함
- 를 생성하면 이 보다 좋은 정책이기 때문에, 즉 가 성립하기 때문에 정책의 개선이 발생함
- 이렇게 이 생성되면 에 대해 다시 정책 평가를 진행함. 즉, 정책의 평가와 개선을 반복
- 처음에는 정책 를 임의의 정책으로 초기화해놓고 시작함
- 어느 순간 정책도 변하지 않고, 그에 따른 가치도 변하지 않는 단계에 도달하게 되어 수렴하는 곳이 바로 최적 정책(optimal policy)과 최적 가치(optimal value)가 됨
정책 평가 부분을 간소화 하기 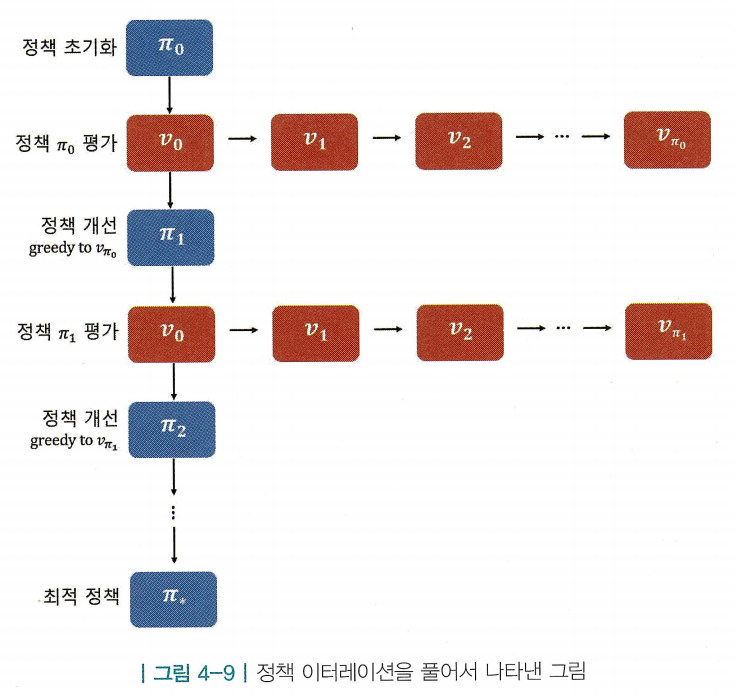
- 세로로 이어지는 루프 안에 가로로 이어지는 루프가 포함되어 있음
- 위 루프에서 연산을 가장 많이 필요로 하는 단계는 사실 “정책 평가”단계임
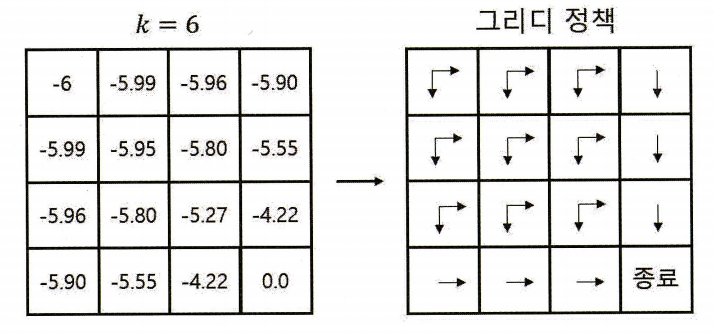
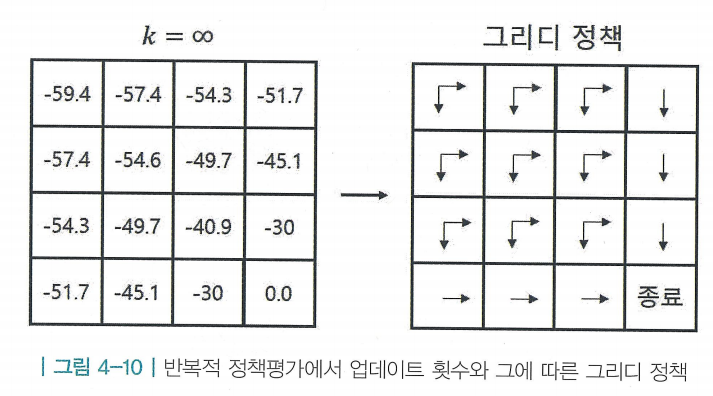
- 그림 4-10에 경우 k=6까지만 진행하여도 그에 따른 그리디 정책이 이미 최적 정책에 도달함
- 즉 가치 함수를 끝까지 학습하지 않아도 됨 (early stopping)
4.3 최고의 정책 찾기 - 밸류 이터레이션
- 정책 이터레이션은 단계마다 서로 다른 정책의 가치를 평가함. 개선 단계를 지날때 마다 새로운 정책이 나오고, 평가 단계에선 방금 만들어진 새로운 정책의 밸류를 평가했기 때문
- 하지만, 밸류 이터레이션(value iteration)은 오로지 최적 정책이 만들어내는 최적 밸류 하나만 확인함
- 최적 밸류(optimal value) : 존재하는 모든 정책들 중 가장 보상을 많이 받을 수 있는 정책(최적 정책)을 따랐을 때 얻는 밸류
- 하지만, 밸류 이터레이션(value iteration)은 오로지 최적 정책이 만들어내는 최적 밸류 하나만 확인함
- 밸류 이터레이션 또한 테이블 기반 방법론 사용 > 테이블 초기화
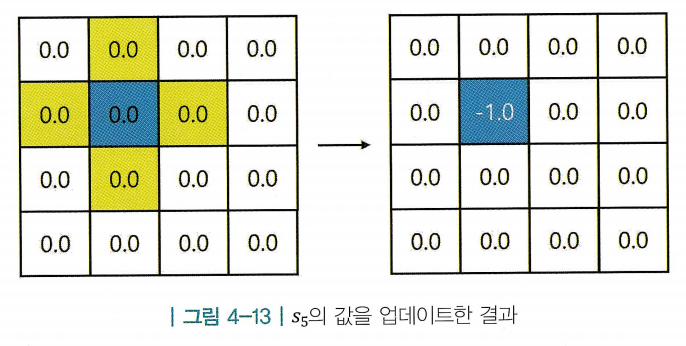
- 아까와 같이 의 값을 업데이트하지만, 주어진 정책이 따로 없음
- 반복적 정책 평가에서는 가 주어져 있기 때문에 벨만 기대 방정식을 사용함. 하지만, 지금은 테이블에서 각 칸은 최적 밸류를 나타내고, 최적 밸류 사이의 관계를 알고 싶은 것이므로 벨만 최적 방정식을 사용함
-
- 그리드 월드는 환경에 확률적인 성질이 없어서 전이 확률은 항상 1임
-
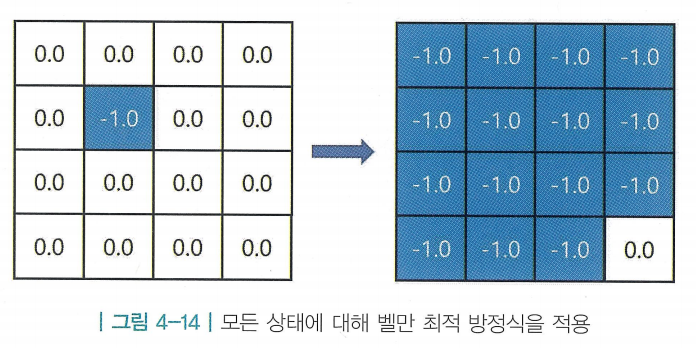
- 같은 방식을 모든 칸에 적용 (종료 상태는 더이상 받을 보상이 없기 때문에 가치가 0으로 고정)
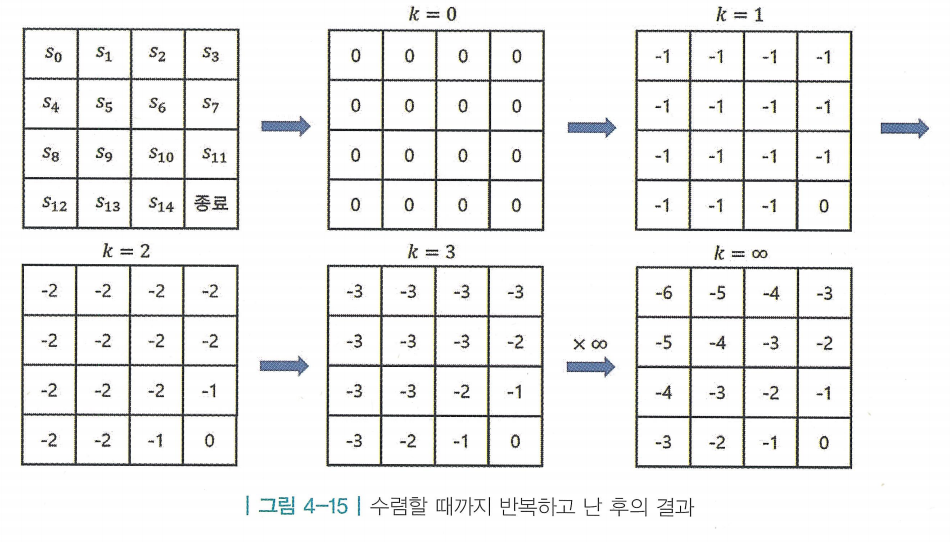
- 같은 방식으로 계속해서 반복하면 테이블의 값들이 수렴하며, 각 상태의 최적 밸류를 의미함
<참고자료>