[바닥부터 배우는 강화학습] - Chapter 5. MDP를 모를 때 밸류 평가하기

MDP의 전이 확률과 보상 함수를 모를 때에 대한 이야기가 시작됩니다. 주어진 수식을 이용해 정확한 값을 계산하는 대신, 수많은 샘플을 통해 근사하는 “샘플 기반 방법론”을 배워봅니다.

---

• 모델프리(Model-Free) : 실제로 액션을 해 보기 전까지 보상을 얼마를 받을지, 어떤 상태로 이동하게 될 지 확률 분포도 모르는 상황
  • 즉, 보상 함수 $r_s^a$와 전이 확률 $P_{ss'}^a$를 모르는 상태
  • “모델을 모른다”, “MDP를 모른다”, “model-free이다” 모두 같은 의미
    
    
• model : 강화학습에서 환경의 모델(model of environment)의 줄임말로, 에이전트의 액션에 대해 환경이 어떻게 응답할지 예측하기 위해 사용하는 모든 것
  • 에이전트의 액션에 대해 환경이 어떻게 반응할지 알 수 있다면 에이전트의 입장에서는 여러 가지 계획(planning)을 세울 수 있음 > 그렇기 때문에 모델을 아는 것이 큰 도움이 됨
    
    
• model-free 상황에서의 prediction, 즉 $\pi$가 주어졌을 때 가치를 평가하는 2가지 방법
  • 몬테카를로, Temporal difference학습
    • 데이블 룩업(table look-up) 방법론 : 테이블을 만들어서 테이블에 값을 기록해놓고 그 값을 조금씩 업데이트 하는 방식

---

5.1 몬테카를로 학습

• 몬테카를로 방법론(Monte Carlo Method) : 무언가 직접 측정하기 어려운 통계량이 있을 때 여러 번 샘플링하여 그 값을 가능하는 기법
  • ex) MCTS(Monte Carlo Tree Search), MCMC(Markov Chain Monte Carlo)
    
    
• MDP에서 각 상태의 가치를 평가할 때 $v_{\pi}(s_t) = \mathbb{E}_{\pi}[G_t]$ 를 사용함. 즉, 리턴을 여러번 계산하여 그 평균을 내면 실제 가치에 수렴함
  • 환경에다가 에이전트를 놓고 경험하도록 하는것 > 에피소드가 끝날 때까지 얻었던 리턴들을 기록해 놓고 평균을 구함
    
    
  • 샘플이 많을수록, 즉 경험을 더 많이 쌓아서 더 많은 에피소드를 진행할수록 대수의 법칙(Law of large numbers)에 의해 각 상태의 밸류 예측치는 점점 정확해 짐 ( ex) 동전의 앞면이 나올 확률)

몬테카를로 학습 알고리즘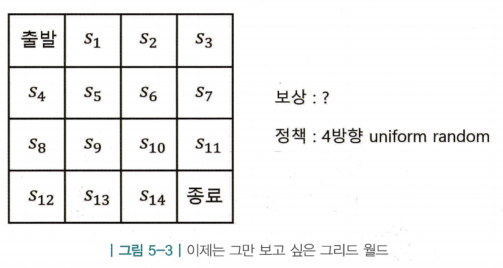

• model-free에서는 보상함수와, 전이확률을 모르지만, 실제 MDP에는 고정된 $r_s^a$와 $P_{ss'}^a$가 존재
  • 보상과 전이확률을 모르기 때문에 실제 에이전트를 환경에 두고 경험을 쌓게 해야함
    • 4방향 랜덤 정책을 통해 돌아다니며 보상과 상태 전이에 대한 경험을 쌓음

1. 테이블 초기화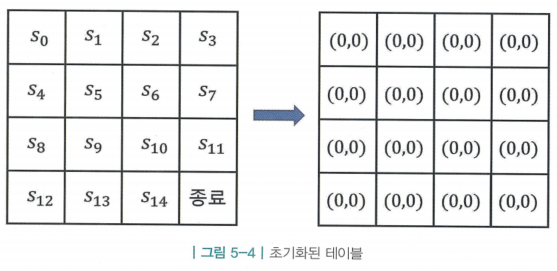

• 테이블에 각 상태별로 N(s)와 V(s) 2개의 값이 필요함
  • N(s) : s를 총 몇 번 방문했는지 계산하기 위해 필요한 값, 상태 s를 한 번 방문 할 때마다 1을 더해줌
  • V(s) : 해당 상태에서 경험했던 리턴의 총합을 기록하기 위해 필요한 변수

2. 경험 쌓기

• 정책 $\pi$를 이용해 움직이는 에이전트를 환경인 그리드 월드의 출발점 $s_0$에 두고 시작함 (정책은 어떤 정책이든 상관 없음)
  • 에이전트는 $s_0$부터 시작하여 액션 $a_0$를 정하고, 그에 따른 보상 $r_0$를 받고 $s_1$에 도착함
    
    
• 이를 반복하여 랜텀 에이전트가 $s_T$에 도달할 때 까지 계산함
  • $s_0, a_0, r_0, s_1, a_1, r_1, s_2, a_2, r_2, \dots, s_{T-1}, a_{T-1}, r_{T-1}, s_T$
    
    
• 이후 각 상태에 대한 리턴을 계산함

  $G_0 = r_0 + \gamma r_1 + \gamma^2 r_2 + \gamma^3 r_3 + \cdots + \gamma^{T-1} r_{T-1}$
  $G_1 = r_1 + \gamma r_2 + \gamma^2 r_3 + \cdots + \gamma^{T-2} r_{T-1}$
  …
  $G_{T-1} = r_{T-1}$
  $G_T = 0$
  

• 여기서 $\gamma$와 보상 $r_0, \ldots, r_{t-1}$는 모두 관측된 숫자 값으로 변수가 아니며, 리턴 또한 모두 그냥 숫자 값임

3. 테이블 업데이트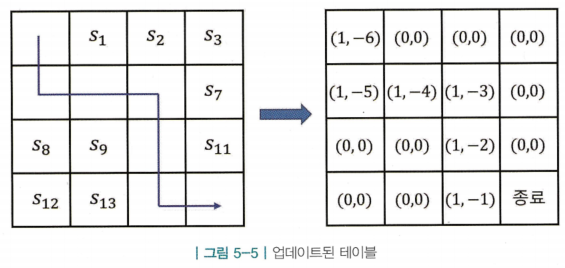

• 앞의 2 단계에서 지나온 경로가 $s_0 \rightarrow s_4 \rightarrow s_5 \rightarrow s_6 \rightarrow s_{10} \rightarrow s_{14} \rightarrow$ 종료라고 가정함
  • 이미 각 상태에 따른 리턴도 계산이 된 상태 → 해당 에피소드에서 방문했던 모든 상태에 대해 해당 칸의 $N(s)$와 $V(s)$ 값이 업데이트됨
    
    
• $N(s_t) \leftarrow N(s_t) + 1$
• $V(s_t) \leftarrow V(s_t) + G_t$
  • 위 과정을 진행하고 나면 테이블의 값이 그림의 오른쪽과 같이 변경됨 (모든 상태의 보상은 -1, $\gamma$는 1로 계산)

4. 밸류 계산

• 2 ~ 3과정을 충분히 반복 > 최종적으로 모든 상태 s에 대해 리턴의 평균을 구함
  • $v_\pi(s_t) \approx \dfrac{V(s_t)}{N(s_t)}$
    • 각 상태의 밸류에 대한 근사치임 > 몬테카를로 방법론

조금씩 업데이트하는 버전

• Monte Carlo Method(MC)와 본질은 같이만 계산하는 방식이 다른 버전
  • 에피소드가 다 끝난 후에 평균을 내는 것이 아닌, 에피소드가 1개 끝날 때마다 테이블의 값을 조금씩 업데이트하는 버전
    
    
  • 이 방식은 카운터를 위한 $N(s_t)$의 값을 따로 저장해 둘 필요 없이 에피소드가 하나 끝날 때 테이블의 값을 업데이트함
    
    
  • $V(s_t) \leftarrow V(s_t) + \alpha (G_t - V(s_t))$
    • $G_t$가 $V(s_t)$보다 크면 $\alpha$에 곱해진 값이 양수가 되어서 기존의 $V(s_t)$ 값을 더 크게 만듬

몬테카를로 학습 구현 MC&TD CODE - Colab

• MC를 통해 prediction을 구현
  • 목표는 그리드 월드에서 4방향 랜덤 정책의 상태별 가치를 구하는 것
    • 환경 : 에이전트의 액션을 받아 상태변이를 일으키고, 보상을 줌
    • 에이전트 : 4방향 랜덤 정책을 이용해 움직임
    • 경험 쌓는 부분 : 에이전트가 환경과 상호작용하며 데이터를 축적
    • 학습하는 부분 : 쌓인 경험을 통해 테이블을 업데이트
      
      
  • 환경에 특별한 확률적 요소 제거, 스텝마다 보상은 -1로 고정
    
    

MC 학습결과

---

5.2 Temporal Difference 학습

• MC의 단점 : 업데이트를 하려면 에피소드가 끝날 때까지 기다려야함
  • 업데이트를 위해 리턴이 필요한데 에피소드가 끝나기 전까지 알 수 없기 때문에 MC는 적용할 수 있는 확경이 제한적임
  • 즉, 반드시 종료하는 MDP(terminating MDP)에서만 사용가능 > 실제 세계에서는 종료조건이 없는 MDP가 대부분임
    
    
• Temporal Difference 학습 방법론(TD) : “추측을 추측으로 업데이트 하자”
  • 에피소드가 끝나기 전에 밸류 값을 업데이트하고 싶다면 종료하지 않는 MDP(non-terminating MDP)에서도 학습 가능 ( ex) 비가 올 지 추측하는 상황)
    
    
• 즉, 미래의 추측으로 과거의 추측을 업데이트하는 것. Temporal Difference > 시간적인 차이를 의미
  • 한 스텝이 지나고 시간이 흐르면 좀 더 정확한 추측을 할 수 있게 되고, 이를 업데이트에 활용함

이론적 배경

• MC의 이론적 근거
  • MC는 리턴 여러개를 모아서 평균을 냄
    
    
  • $v_\pi(s_t) = \mathbb{E}_\pi[G_t]$
    • 가치 함수의 정의가 리턴 $G_t$의 기댓값이기 떄문에 $G_t$를 많이 모으면 모을수록 그 평균은 $V_{\pi}(s_t)$에 수렴하게됨
      
      
  • 통계학 용어로 “$G_t$는 $v_\pi(s_t)$의 불편 추정량(unbiased estimate)”이라고 함
    • 불편, 즉 편향되지 않고 올곧은 추정량이라는 뜻
      
      
      
• TD의 이론적 근거
  • 벨만 기대 방정식 0단계 : $v_{\pi}(s_t) = \mathbb{E}_{\pi}[r_{t+1} + \gamma v_{\pi}(s_{t+1})]$
    
    • $r_{t+1} + \gamma v_{\pi}(s_{t+1})$을 여러번 뽑아서 평균을 내면 그 평균은 $v_{\pi}(s_t)$에 수렴함
      
      
    • $r_{t+1} + \gamma v_{\pi}(s_{t+1})$의 기대값이 곧 $v_{\pi}(s_t)$이기 때문임
      
      • 즉, $r_{t+1} + \gamma v_{\pi}(s_{t+1})$는 목표치가 되는 값이기 때문에 이 값을 TD 타깃(TD target)이라고 함
        
        
    • MC에서 리턴을 여러개 모았던것 처럼 $r_{t+1} + \gamma v_{\pi}(s_{t+1})$의 값을 여러개 모으되, 한 개씩 얻을 때마다 테이블에 쓰여 있던 값을 조금씩 업데이트 함

Temporal Difference 학습 알고리즘

• TD도 MC와 마찬가지로 테이블의 값을 초기화하는 것부터 시작함
  • 각 상태에 대해 그 값을 0으로 초기화 > 에이전트를 $s_0$에 두고 경험을 쌓게함 (MC, TD 동일)
  • TD와 MC의 차이는 업데이트 수식과 업데이트 시점임
    
    
• $S_0 \rightarrow S_1 \rightarrow S_2 \rightarrow S_3 \rightarrow S_7 \rightarrow S_6 \rightarrow S_{10} \rightarrow S_{11} \rightarrow \text{종료}$
  • 위 경로를 가정했을때 총 8번의 상태 전이가 발생함. TD는 종료 상태에 도달하기 이전에 즉 각각의 상태 전이가 일어나자마자 바로 테이블의 값을 업데이트함

$MC :\ V(s_t) \leftarrow V(s_t) + \alpha,(G_t - V(s_t))$
$TD :\ V(s_t) \leftarrow V(s_t) + \alpha,(r_{t+1} + \gamma V(s_{t+1}) - V(s_t))$

• 원래 MC에서의 정답이었던 $G_t$의 자리를 대신하여 $r_{t+1} + \gamma v_{\pi}(s_{t+1})$가 들어감
  • 이 업데이트 식을 이용하여 다음과 같이 8번 업데이트 진행

    $V(s_0) \leftarrow V(s_0) + 0.01 \ast (-1 + V(s_1) - V(s_0))$
    $V(s_1) \leftarrow V(s_1) + 0.01 \ast (-1 + V(s_2) - V(s_1))$
    $\ldots$
    $V(s_{11}) \leftarrow V(s_{11}) + 0.01 \ast (-1 + V(s_{15}) - V(s_{11}))$

Temporal Difference 학습 구현
MC&TD CODE - Colab

TD 학습결과

---

5.3 몬테카를로 vs TD

• MC와 TD는 문제와 상황에 따라 각자의 장점이 다름

학습 시점

• Episodic MDP
  • MDP의 상태들 중에 종료 상태(terminating state)라는 것이 있어서 에이전트의 경험이 에피소드 단위로 나뉘어질 수 있는 것
• Non-Episodic MDP
  • 종료 상태 없이 하나의 에피소드가 무한히 이어지는 MDP
    
    
• 종료 조건이 명확한 경우 Episodic MDP형태로 만들 수 있지만, 종료 조건이 없거나, 하나의 에피소드가 너무 길어지는 경우가 존재
  • MC는 Episodic MDP에만 적용할 수 있지만, TD는 어떤 MDP는 적용 가능

편향성(Bias)

• MC : $v_{\pi}(s_t) = \mathbb{E}[G_t]$ (from 가치 함수의 정의)
• TD : $v_{\pi}(s_t) = \mathbb{E}[r_{t+1} + \gamma v_{\pi}(s_{t+1})]$ (from 벨만 기대 방정식)
  
  
• MC는 리턴의 평균을 향해 업데이트됨 > 가치 함수의 정의가 애초에 리턴의 기댓값이기 때문
  • 즉, 샘플이 모일수록 그 평균은 실제 가치에 수렴함 > 편향되어 있지 않은(unbiased) 안전한 방법론임
    
    
• TD는 현재의 추측치를 다음 스텝의 추측치로 업데이트함 > TD타깃과 현재 추측치 사이 차이를 줄여주는 방향으로 업데이트함
  • 실제 벨만의 식안에는 $r_{t+1} + \gamma v_{\pi}(s_{t+1})$이지만, 업데이트에 사용하는 수식은 $r_{t+1} + \gamma V(s_{t+1})$임
    • 정책 $\pi$의 값을 모르기 때문 > 업데이트 방향이 “안전”하지못함
      
      
  • $V(s_{t+1}) \ne v_{\pi}(s_{t+1})$
    • 대문자 $V$와 소문자 $v_{\pi}$를 구분하는 이유. 따라서 실제 TD 타깃인 $r_{t+1} + \gamma v_{\pi}(s_{t+1})$는 불편 추정량(unbiased estimate)이지만, 우리가 사용하는 TD 타깃인 $r_{t+1} + \gamma V(s_{t+1})$은 편향(biased)됨
      
      
• 즉, TD타깃은 샘플을 무한히 모아서 지속적으로 업데이트해도 실제 가치에 다가가리라는 보장이 없음
  • (테이블 룩업과 하나의 조건(TD-zero)이 추가로 붙고, neural network를 도입하면 어느정도 해결가능함)

분산(Variance)

• MC는 리턴을 통해 업데이트됨 > 리턴이라는 하나의 값을 관찰하기까지 수많은 확률적 과정을 거쳐야함
  • 리턴을 얻으려면 에피소드 하나가 끝나야 하는데, 수많은 상태 전이와 정책 $\pi$로 이루어져 있음
    • 즉, 평균으로부터 각각의 값들이 멀리 퍼져있을 수 있다는 뜻 > 분산(Variance) 혹은 변동석이 크다는 것
      
      
• TD는 한 샘플만 보면 바로 업데이트가 가능하기 때문에 분산이 작음
  • MC가 수십~수백 개의 확률적(stochastic)결과로 이루어진다면 TD는 딱 한 걸음을 떼는 것이 전부임
  • TD는 값들이 평균 근처에 몰려있고, 즉 분산이 작음

---

5.4 몬테카를로와 TD의 중간?

• MC는 편향성이 없다는 장점이 있고, TD는 변동성이 적다는 장점이 있음
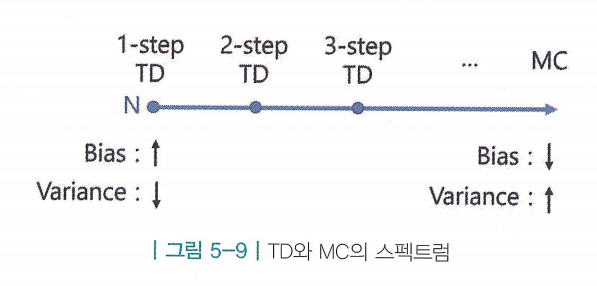
  • “MC와 TD의 중간은 없을까?” > n-step TD

n 스텝 TD

• $r_{t+1} + \gamma V(s_{t+1})$ : TD에서 한 스텝만큼 진행하여 가치를 평가한것
  
  
• 이와 같은 방법으로 3-step, 4-step, … , n-step을 진행하고 난 뒤 추측치를 이용할 수 있음

  $N = 1 :\ r_{t+1} + \gamma V(s_{t+1})$
  $N = 2 :\ r_{t+1} + \gamma r_{t+2} + \gamma^{2} V(s_{t+2})$
  $N = 3 :\ r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \gamma^{3} V(s_{t+3})$
  …
  $N = n :\ r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \cdots + \gamma^{n} V(s_{t+n})$

• 모든 값은 TD타깃이 될 수 있으며 > 각 타깃 값을 n-step return이라고 부름
  • $N = \infty :\ r_{t+1} + \gamma r_{t+2} + \gamma^{2} r_{t+3} + \cdots + \gamma^{T-1} R_{T}$
    
    
• 결국 n-step에서 n이 무한으로 가면 리턴과 동일해짐 > MC 방식
  • 즉, $N = 1$인 경우 TD-zero 이며, $N = \infty$인 경우 MC인 것
    • TD-zero : n=1인 경우 TD 타깃을 이용하여 업데이트하는 방법론. TD(0)라고 표기하며 TD-zero라고 읽음

• `n에 따라서 편향성(bias)와 분산(Variance)에 관한 성질이 바뀜
  • MC에 가까워질수록 한 번 업데이트할 때 쓰이는 값의 비중에서 추측이 차지하는 비중이 줄어들고, 실제 보상값이 차지하는 비중이 늘어남
    
    
  • 그렇기 때문에 적절한 n의 값을 찾는것이 핵심임