[바닥부터 배우는 강화학습] - Chapter 6. MDP를 모를 때 최고의 정책 찾기

방선생·2025년 11월 7일
bookreinforcement learning

바닥부터 배우는 강화학습

목록 보기
6/6

이전 챕터에서 Prediction 문제를 풀었다면 이번 챕터에서는 Control 문제를 해결할 차례입니다. 밸류를 계산할 수 있기 떄문에 이를 이용해 정책을 찾는 것은 한결 쉽습니다. 그 유명한 Q러닝도 이번 챕터에서 등장합니다.

  • 주어진 정책을 평가하는 방법론인 MC와 TD를 통해 어떤 정책이 주어져도, 혹은 MDP에 대한 정보를 몰라도 각 상태의 가치를 평가할 수 있음
  • MDP에 대한 정보(상태 전이 확률과 보상 함수)를 전혀 모르는 상황에서 control 방법 중 가장 대표적인 3가지 방법론 : Monte Carlo Control, SARSA, Q Learning

6.1 몬테카를로 컨트롤

  • MDP를 알때에 최적 정책을 찾는 방법
    • 정책 이터레이션 : 임의의 정책에서 시작 > 정책 평가 > 밸류 계산 > 계산한 밸류에 대한 그리디 정책 업데이트 > 반복

정책 이터레이션을 그대로 사용할 수 없는 이유

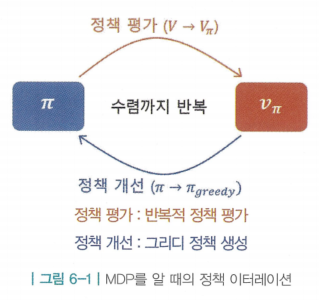
  • 평가 단계에서는 반복적 정책 평가를, 개선 단계에서는 그리디 정책 생성을 이용함
    • 하지만 model-free 상황에서는 사용할 수 없음

1. 평가 단계에서 반복적 정책 평가를 사용할 수 없음

  • vπ(s)=∑a∈Aπ(a∣s)(rsa+γ∑s′∈Spss′avπ(s′))v_\pi(s) = \sum_{a \in A} \pi(a|s) \left( r_s^a + \gamma \sum_{s' \in S} p_{ss'}^a v_\pi(s') \right)
    • (반복적 정책 평가의 핵심인 벨만 기대 방정식 2단계)
    • 위 식을 보면 MDP를 알아야만 함 (rsar_s^a, pss′ap_{ss'}^a의 대한 값)

  • 보상을 알려면 직접 액션을 통해 값을 받아야하며 다음 상태가 어디가 될지도 실제로 액션을 통해 어디 도착하는지 봐야함
    • 또한 도착했다는 정보만 알 수 있을 뿐 얼마의 확률로 이상태에 도착했는지, 다른 상태에 도착할 확률을 얼마인지 등에 대한 정보를 알수 없음
    • 따라서 정책 평가 단계에서 반복적 정책 평가를 사용할 수 없음

2. 개선 단계에서 그리디 정책을 생성할 수 없음

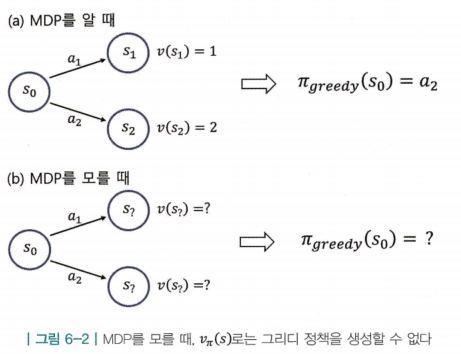
  • 어떻게든 정책 평가를 진행한 상황이라고 가정을 하더라도, MDP의 상태 전이확률을 모르기 때문에 각 액션에 대한 다음 상태가 어디가 될지 알 수 없음
    • 액션을 선택하면 도달하게 되는 상태의 밸류를 통해 액션의 우열을 판단했는데, 이제는 어떤 상태에 도달할지 알 수 없기 때문에 도착하는 상태의 밸류 또한 비교할 수 없음

해결 방법

1. 평가 자리에 MC

  • 정책 평가 단계에서 각 상태의 밸류를 계산하기 위해 반복적 정책 평가를 사용해야 하는게 불가능함
    • MDP를 모를 때 밸류를 계산하는 방법론(지금은 MC)을 평가 단계에서 사용하면 벨만 기대 방정식 2단계 수식들을 사용하지 않아도 각 상태의 밸류를 평가할 수 있음

2. V 대신 Q

  • 상태 가치 함수인 v(s)만 가지고는 정책 개선 단계에서 그리디 정책을 생성 할 수 없음
    • v(s) 대신 상태-액션 가치 함수(q(s,a)q(s,a))를 사용함

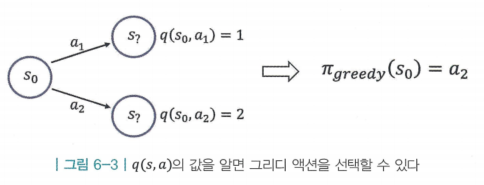
  • 상채 s에서 각 액션을 선택하면 어느 상태로 도달하는지는 모르지만, 각 액션을 선택하는 것의 밸류는 알기 때문에 밸류가 제일 높은 액션을 선택할 수 있음

  • 종합해보면 몬테카를로 방법을 이용하여 q(s,a)를 구하는것이 핵심
    • 이외에는 정책 이터레이션의 방법론과 동일

  • 추가적으로, 강화 학습에서 에이전트가 최적의 해를 찾으려면 에이전트는 주어진 MDP 안의 여러 상태를 충분히 탐색(exploration)해야함
    • 여러 상태를 보고 각 상태에서 여러 액션들을 모두 해봐야 가장 좋은 액션의 시퀀스를 찾아낼 수 있음
      • 만일 어떤 상태를 학습 내내 한 번도 방문해보지 못한다면 그 상태의 가치는 평가할 수 있는 방법이 전무하기 때문
      • 만약 못 가본 상태가 정말 좋은 상태라면 우리의 에이전트는 최적 해를 찾지 못하게 될 수도 있음

3. greedy 대신 ϵ\epsilon-greedy

  • 액션을 항상 그리디하게 선택하면, 다른 액션들이 선택될 기회가 영구히 사라짐 (다른 액션들이 더 좋을 수도 있음에도)
    • 그렇기 때문에 에이전트의 탐색을 보장해 주도록 가치가 높지 않은 다른 액션들을 다양하게 선택해 주어야함. 즉, “탐색의 정도를” 알맞게 맞춰야함

π(a∣s)={1−εif a∗=arg⁡max⁡aq(s,a)εotherwise\pi(a|s) = \begin{cases} 1 - \varepsilon & \text{if } a^* = \displaystyle\arg\max_a q(s,a) \\ \varepsilon & \text{otherwise} \end{cases}

  • ε\varepsilon이라는 작은 확률 만큼 랜덤하게 액션을 선택하고, 1−ε1 - \varepsilon이라는 나머지 확률은 원래처럼 그리디 액션을 선택함
  • 여기서 조금 더 좋은 방법론은 ε의 값을 처음에는 높게 하다가 점점 줄여주는 것임
    • 이를 decaying ε-greedy이라고 하며 몬테카를로 컨트롤을 구현할 때 decaying ε-greedy를 이용함

몬테카를로 컨트롤 구현

  • 몬테카를로 컨트롤 : 정책 평가 단계에서는 MC를 이용하여 q(s,a)를 구하고, 정책 개선 단계에서는 q(s,a)에 대한 ε-greedy 정책을 만듬

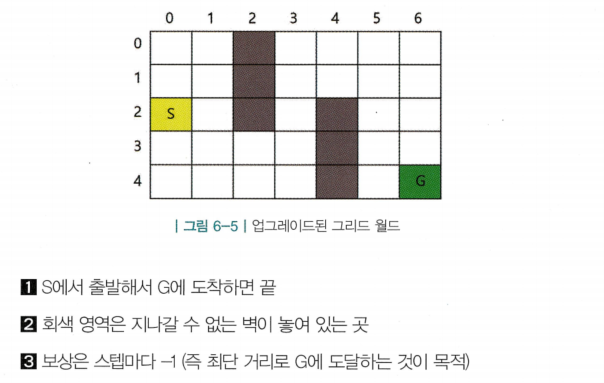
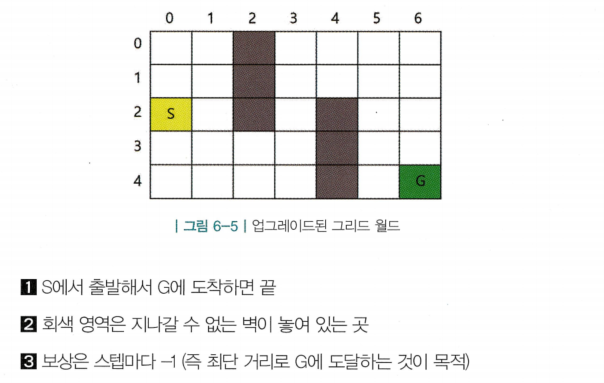
  • 몬테카를로 컨트롤을 구현하기 위해 “업그레이드된 그리드 월드”사용
    • 간략화된 정책 이터레이션을 사용할 예정 (평가와 개선 단계를 끝까지 진행하지 않고 조기 종료)

  • 기존의 정책 이터레이션이 평가 단계를 수렴할 때 까지 진행했던 것과 다르게 평가 단계에서 업데이트를 굳이 수렴할 때까지 하지 않음
    • 가치 테이블에 저장해둔 값들이 조금이라도 바뀌면 그에 대해서 개선 단계를 진행할 수 있기 때문

수렴할 때까지 n번 반복

  • 한 에피소드의 경험을 쌓고
  • 경험한 데이터로 q(s,a)q(s,a) 테이블의 값을 업데이트하고 (정책 평가)
  • 업데이트된 q(s,a)q(s,a) 테이블을 이용하여 ε\varepsilon-greedy 정책을 만들고 (정책 개선)
  • 반복

몬테카를로 컨트롤 구현

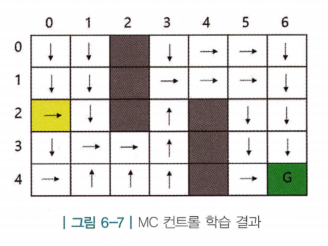
  • 노란색 칸에서 출발하여 화살표만 따라가면 최적의 경로로 초록색 칸에 도달함을 확인할 수 있음
    • 액션을 선택하는 과정에서 ε\varepsilon-greedy라는 확률적 요소가 있기 때문에 에피소드마다 방문하는 상태가 달라지기 때문에 위 학습 결과는 매번 학습을 실행할 때마다 달라질 수 있음

6.2 TD 컨트롤 1 - SARSA

  • 몬테카를로 컨트롤의 핵심은 평가 단계에서 MC를 사용하는 것임
    • “MC 대신 TD를 사용하면 안될까?”

  • TD가 MC에 비해 여러 장점이 존재함
    • 대표적으로 분산이 훨씬 작다거나, 에피소드가 끝나지 않아도 온라인으로 학습할 수 있음

  • 결론적으로, MC든 TD든 결국 실제 밸류에 가까워지도록 테이블의 값을 수정해 나가는 과정인데, TD는 경험으로부터 얻은 샘플을 통해 실제 값을 추측하여 추측치에 가까워지도록 업데이트 하는 방법이기 때문에 가능함

MC 대신 TD

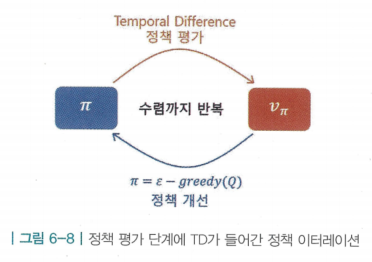
  • 정책 평가 단계에서 MC 대신 TD를 이용. 즉, TD를 이용해 q(s,a)를 구함
    • 이를 SARSA라고 함

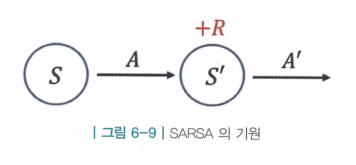
  • 그림과 같이 상태 s에서 액션 a를 선택하면 보상 r을 받고 상태 s'에 도착하고, 상태 s'에서는 다음 액션 a'을 선택함. 이 5개의 알파벳을 이어서 적으면 SARSA가 됨

TD로 V 학습 : V(S)←V(S)+α(R+γV(S′)−V(S))V(S) \leftarrow V(S) + \alpha (R + \gamma V(S') - V(S))

TD로 Q 학습(SARSA) : Q(S,A)←Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))Q(S, A) \leftarrow Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))

  • V가 Q로 바뀐 것을 제외하고 다른것이 없음
  • 벨만 기대 방정식 0단계

TD로 V 학습 : vπ(st)=Eπ[rt+1+γvπ(st+1)]v_\pi(s_t) = \mathbb{E}\pi [r{t+1} + \gamma v_\pi(s_{t+1})]

TD로 Q 학습(SARSA) : qπ(st,at)=Eπ[rt+1+γqπ(st+1,at+1)]q_\pi(s_t, a_t) = \mathbb{E}\pi [r{t+1} + \gamma q_\pi(s_{t+1}, a_{t+1})]

  • 업데이트 식에서 TD 타깃에 해당하는 식이 모두 벨만 기대 방정식으로 나온 것임을 확인할 수 있음
    • 정책 함수 π\pi를 통해 랜덤하게 진행 되다가 한 스텝의 데이터가 생성될 때마다 이 데이터를 통해 TD 타깃을 계산하여 기존의 테이블을 업데이트해 나가는 방식임

SARSA 구현

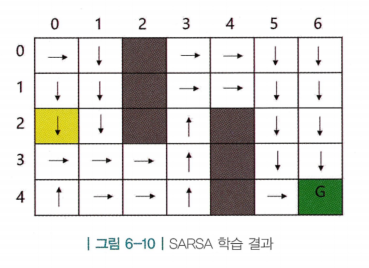
  • 출발지점에서 화살표를 통해 도착 지점까지 최단경로를 찾음. 즉, 최적해(optimal solution)를 찾는 과정
    • 하지만, 학습과정에서 어떤 상태를 얼마나 탐색(exploration)했는가에 따라 경로 바깥의 칸들의 최적 액션은 가끔 이상한 방향을 가리키기도함. 즉, 다양한 상태를 충분히 여러번 방문하도록 보장하는것이 중요

6.3 TD 컨트롤 2 - Q러닝

  • Q 러닝도 마찬가지로 TD를 이용하여 최적의 정책을 찾는 방법
    • 처음으로 강화 학습이 딥러닝과 결합되어 성과를 나타낸 연구가 Q러닝을 이용함
    • 딥러닝을 도입하지 않은 Q러닝은 여전히 테이블을 만들어서 Q함수를 기록하고, 그 값을 업데이트 하는 방식으로 학습함

off-Policy와 on-Policy

On-Policy : 타깃 정책과 행동 정책이 같은 경우(직접 경험)

Off-Policy : 타깃 정책과 행동 정책이 다른 경우(간접 경험)

  • 타깃 정책(target policy) : 강화하고자 하는 목표가 되는 정책
    • 학습의 대상이 되는 정책이고, 계속해서 업데이트 됨에 따라 점점 강화되는 정책

  • 행동 정책(behavior policy) : 실제로 환경과 상호 작용하며 경험을 쌓고 있는 정책

  • Off-Policy 강화 학습과 지도학습은 다름
    • 만약 타깃 정책이 행동 정책을 그대로 따라한다면 지도학습으로 볼수 있지만, Off-Policy는 그대로 따라하는 것이 아닌 행동 정책을 보고 따로 학습하는 것이기 때문에 차이가 존재함

    • 즉, 모든 행동을 그대로 따라하는 것이 아닌 행동을 보고 배우는 것 (좋은 결과는 배우고, 좋지 않은 결과는 수정함)

off-Policy 학습의 장점

  • 가정 : 에이전트의 초기 정책 함수 π0\pi_0 이며, 이 에이전트를 환경에다가 가저 놓고 경험을 쌓게 함
    • 경험은 트랜지션 단위로 나누어 (s,a,r,s’)으로 표현

1. 과거의 경험을 재사용할 수 있다

  • π0\pi_0를 업데이트 하기 위해 경험을 쌓고 π1\pi_1으로 조금 업데이트를 진행
    • on-policy의 경우 π1\pi_1를 학습하려면 π1\pi_1를 활용하여 처음부터 다시 학습해야함
      • π0\pi_0과 π1\pi_1은 다른 정책이기 때문
      • 이는 데이터의 효율성 측면에서 단점임

    • off-policy의 경우 타깃 정책과 행동 정책이 달라도 되기 때문에 과거의 정책인 π0\pi_0가 경험한 샘플들을 π1\pi_1의 업데이트에 그대로 재사용할 수 있음
      • 즉, π1000\pi_{1000}까지 가더라도 π0\pi_0에서 쌓은 데이터를 재사용할 수 있음

2. 사람의 데이터로부터 학습할 수 있다

  • off-policy는 행동 정책에 어떤 정책이든 가져올 수 있음
    • (행동 정책과 타깃정책 사이의 차이가 얼마나 큰지에 따른 학습 효율성은 달라질 수 있음)
    • 행동 정책은 그저 환경과 상호작용하며 경험을 쌓을 수만 있으면 됨. 즉, 다른 행동 정책의 종류에 제약이 없다는 뜻

  • 보통 에이전트는 랜덤 정책으로 초기화 하고 학습을 진행 하지만, 양질의 데이터를 학습에 사용한다면 더욱 학습 속도를 올릴 수 있음

3. 일대다, 다대일 학습이 가능하다

  • 동시에 여러 개의 정책을 학습시킨다고 가정했을때, Off-policy 학습을 이용하면 이중에서 단 1개의 정책만 경험을 쌓게 두고, 그로부터 생성된 데이터를 이용해 동시에 여러 개의 정책을 학습시킬 수 있음
    • 반대로 동시에 여러 개의 정책이 겪은 데이터를 모아서 단 1개의 정책을 업데이트할 수도 있음

  • 에이전트의 정책은 굉장히 실험적인 행동을 하여 다양한 경험에 쌓는데 특화되게 하고, 다른 에이전트의 정책은 현재까지 알고 있는 정보를 바탕으로 최고의 성능을 내는 데 집중한다면 두 에이전트가 겪는 경험의 질은 전혀 다르게됨 (즉, 다양한 관점에서 자유롭게 학습할 수 있음)

  • SARSA 알고리즘이 on-policy 알고리즘이라고 한다면, Q러닝은 바로 off-policy 알고리즘으로 볼 수 있음



Q러닝의 이론적 배경 - 벨만 최적 방정식

q∗(s,a)=max⁡πqπ(s,a)q_*(s, a) = \max_{\pi} q_{\pi}(s, a)

  • 벨만 최적 방정식에서 q∗q_*를 알게 되는 순간, 주어진 MDP에서 순간마다 최적의 행동을 선택할 수 있음
    • ∗q∗∗*q_**의 값이 가장 높은 액션을 선택하면 되기 때문

  • π∗=arg⁡max⁡aq∗(s,a)\pi_* = \arg\max_a q_*(s, a)
    • 즉, 최종 목적은 최적의 액션-가치 함수인 q∗q_*를 찾는 것임

q∗(s,a)=rsa+γ∑s′∈Spss′amax⁡a′q∗(s′,a′)q_*(s, a) = r^a_s + \gamma \sum_{s' \in S} p^a_{ss'} \max_{a'} q_*(s', a')

(벨만 최적 방정식 2단계)

  • q(s,a)q_(s, a)가 q(s′,a′)q_(s', a')과 어떤 관계에 있는지를 재귀적으로 나타내는 식
    • 하지만 MDP에 대한 정보를 전혀 모르기 때문에 위의 식을 그대로 이용할 수는 없음
    • 실제 액션을 해보기 전까지는 다음 상태가 어디가 될지, 보상은 얼마나 받을지 알 수 없기 때문

q∗(s,a)=Es′[r+γmax⁡a′q∗(s′,a′)]q_*(s, a) = \mathbb{E}_{s'} [r + \gamma \max_{a'} q_*(s', a')]

(벨만 최적 방정식 0단계)

  • 여러 개의 샘플을 이용해서 계산하고, 여러 번 경험을 쌓은 다음에 각 경험으로부터 얻은 기댓값 연산자 안의 항을 평균내면, 그 평균이 대수의 법칙에 의해 실제 기댓값으로 다가간다는 성질을 이용

  • 즉, 위 식을 이용하여 TD학습을 진행만 하면 됨
    • q∗(s,a)q_*(s, a)의 값을 담아 놓기 위한 테이블 생성하고, r+γmax⁡a′q∗(s′,a′)r + \gamma \max_{a'} q_*(s', a')를 정답이라고 가정하고 그 방향으로 조금씩 업데이트해 나가도록 함

SARSA : Q(S,A)←Q(S,A)+α(R+γQ(S′,A′)−Q(S,A))Q(S, A) \leftarrow Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))

Q러닝 : Q(S,A)←Q(S,A)+α(R+γmax⁡A′Q(S′,A′)−Q(S,A))Q(S, A) \leftarrow Q(S, A) + \alpha (R + \gamma \max_{A'} Q(S', A') - Q(S, A))

  • Q러닝 식에서 TD 타깃 부분 벨만 최적 방정식의 기댓값 안의 항을 그대로 옮겨 적은 것

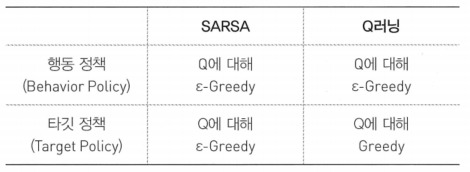
  • SARSA의 경우 해동 정책과 타깃 정책이 같지만, Q러닝의 경우 행동 정책과 타깃 정책이 다름
    • 행동 정책에는 탐험을 위한 ε\varepsilon값이 들어가 있는 반면, 타깃 정책은 순수하게 가장 Q값이 높은 액션을 선택하는 방식인 그리디 정책을 따름 (행동 정책과 타깃 정책이 다름)

왜 Q러닝은 off-policy 학습이 가능한가?

SARSA : qπ(st,at)=Eπ[rt+1+γqπ(st+1,at+1)]\text{SARSA : } q_{\pi}(s_t, a_t) = \mathbb{E}_{\pi}[r_{t+1} + \gamma q_{\pi}(s_{t+1}, a_{t+1})] (벨만 기대 방정식)

Q러닝 : q∗(s,a)=Es′[r+γmax⁡a′q∗(s′,a′)]\text{Q러닝 : } q_*(s, a) = \mathbb{E}_{s'}[r + \gamma \max_{a'} q_*(s', a') ] (벨만 최적 방정식)

  • (Eπ\mathbb{E}_\pi와 Es′\mathbb{E}_{s'}에 차이점 존재)

  • 둘 다 기대값 연산자이지만 Eπ\mathbb{E}_\pi는 정책 함수 π\pi를 따라가는 경로에 대해서 기댓값을 취하라는 의미임
    • 그러나 해당 값을 얻는 데에 정책 함수 π\pi의 확률적인 요소가 포함되어 있음
      • 정책에 의한 확률적인 요소 π(a∣s)\pi(a|s)와 환경에 의한 확률적인 요소 pss′ap_{ss'}^{a}
      • 즉, Eπ\mathbb{E}_\pi의 의미는 이 두 요소를 모두 고려하여 기댓값을 구하라는 것임

    • 샘플 기반 방법론을 통해서 π\pi가 주어진 환경 위에서 동작한 여러 개의 샘플을 통해 평균 내는 방식으로 위 기댓값을 계산함


  • 반면 Es′\mathbb{E}_{s'}는 정책 π\pi와 아무런 관련이 없는 항임
    • 벨만 최적 방정식 2단계 수식을 보면 pss′ap_{ss'}^{a}만 있을 뿐 π\pi와 관계된 항이 없음

    • 즉, Es′\mathbb{E}_{s'}를 계산할 때에 어떠한 정책을 사용해도 상관없다는 것을 의미함
      • 임의의 정책을 사용하여 주어진 환경 안에서 데이터를 모으면, 그 데이터 안에 pss′ap_{ss'}^{a}가 모두 반영되어 샘플이 모이고, 샘플을 이용하여 기댓값을 계산할 수 있음

    • 벨만 최적 방정식은 해당 환경에서 존재하는 이 세상 모든 정책 중에서 “최적의 정책”에 대한 식이기떄문에 최적 정책은 환경에 의존적(dependent)임

Q러닝 구현

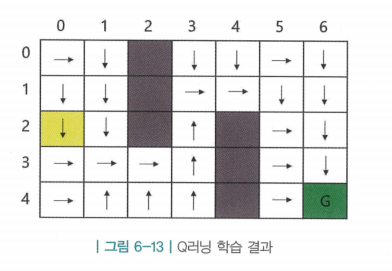
  • 마찬가지로 최적 해를 잘 찾는 것을 확인 할 수 있음
    • MC컨트롤과 SARSA의 최적 경로와 각각의 화살표 방향이 조금씩은 다르지만, 결국 시작 지점에서 목표 지점까지 가는데 걸리는 칸 수는 동일함
    • 즉, 주어진 환경에 최적 경로가 여러 개 있으며, 각각의 방법론이 서로 다른 최적 정책으로 수렴했다는 뜻임







profile
방선생
AI & Robotics
이전 포스트

[바닥부터 배우는 강화학습] - Chapter 5. MDP를 모를 때 밸류 평가하기

0개의 댓글