Continual Learning of Neural Machine Translation within Low Forgetting Risk Regions

Continual Learning of Neural Machine Translation within Low Forgetting Risk Regions

EMNLP 2022

분야 및 배경지식

• Continual Learning
  • memory replay
    • 이전에 학습한 데이터의 일부를 새로운 태스크를 학습할 때 사용
    • 학습 비용이 높아질 수 있으며, 이전의 데이터에 접근할 수 없는 경우 존재
  • pseudo memory replay
    • 이전 태스크에 해당하는 pseudo data를 만들어 새로운 태스크를 학습할 때 사용
    • 이전 태스크와 새로운 태스크가 유사해야 잘 작동
  • model separation
    • 모델에 특정 태스크를 위한 파라미터를 추가하고 새로운 태스크 데이터에 대해 해당 파라미터만 학습
    • 모델의 크기를 늘리며 input sentence가 어떤 태스크에 해당하는지 모델이 알아야 함
  • regularization
    • auxiliary(예비의, 보조의) loss를 활용한 multi-objective learning
    • 근사치로 계산된 loss는 볼록하고 대칭적이나, 실제 loss는 대부분 반드시 그렇진 않음
    • multi-objective learning으로 파라미터가 특정 지역에 수렴(converge)되는 것이 반드시 forgetting 문제를 완화하는 방향으로 진행되는 것은 아님
• Hessian and Fisher Information Matrices
  • Hessian Matrix
    • 두번 미분 가능한 loss L에 대해서, Hessian Matrix는 weights에 대한 loss function의 이계도함수의 행렬 (matrix of second-order derivatives of the loss function with respect to the weights)
    • 직관적으로, 주어진 포인트 theta 주변 loss의 곡률을 표현해주는 역할을 수행
    • 값이 작을수록 loss는 더 평평하며, 평평할수록 loss의 변화가 적음
  • Fisher Information Matrix
    • 직관적으로, Hessian Matrix와 유사한 역할을 수행
    • empirical training distribution으로 model distribution을 대체할 수 있음

문제점

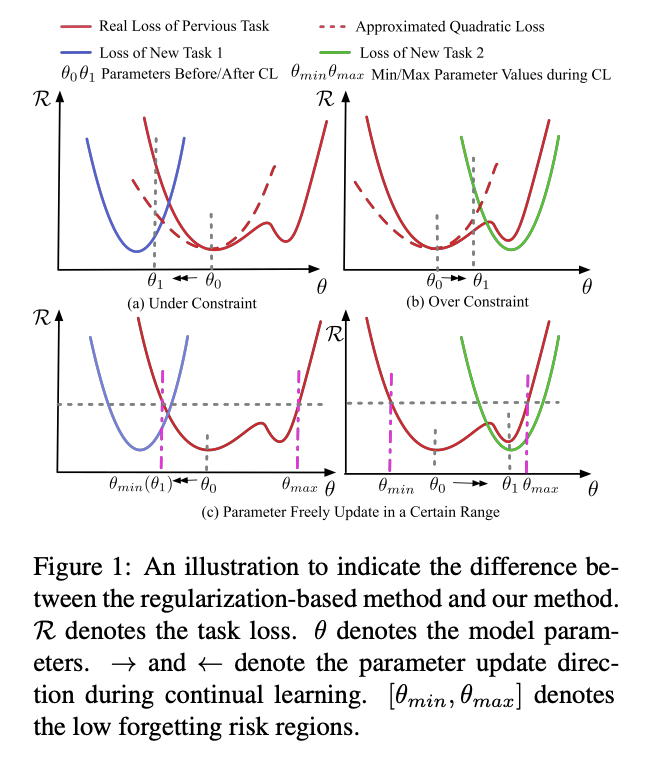
• Continual Learning의 regularization-based 방식은 잘못된 측정(misestimate)을 야기할 수 있으며, 이전 태스크와 새로운 태스크 사이에 균형을 맞추기 어려움

해결책

• 실제 loss의 local feature에 기반한 2단계 학습

1. search low forgetting risk region

Curvature-based Method

• 이전 태스크의 loss에 최소한의 영향만을 끼치는 파라미터를 찾음
• loss의 곡률(curvature) 활용
  • curvature는 최초의 파라미터 theta-0 주변의 파라미터가 변화함에 따라 얼마나 빠르게 loss가 변화하는지를 측정
  • curvature가 작은 파라미터가 forgetting을 최소화하고 안전하게 업데이트 가능

Output-based Method

• 이전 태스크의 모델 아웃풋에 대한 파라미터의 영향력(impact) 활용
• 모델이 자동으로 파라미터의 update region을 찾고자 함 (objective learning)
  • first term of objective = KL divergence
    • 이전 태스크에 대한 모델의 아웃풋이 사전학습 모델과 최대한 유사하도록
  • second term of objective = L2 norm
    • 모델 파라미터가 greedy하게 변화해 region의 크기를 가능한 최대화하도록

2. continually train the model within this region only with the new training data

• 위에서 찾은 low forgetting risk region([min_theta, max_theta])에 대해서만 파라미터 업데이트
• 새로운 태스크의 gradient 활용하여 업데이트, region 밖에 대해서는 업데이트 미진행
• 거대한 규모의 NMT 모델의 경우 over-parameterize 되어있고 많은 파라미터가 충분한 지식을 학습하지 못했다는 사실을 염두에 둔다면 이러한 hard-constrained 학습 방식은 대부분의 경우 모델이 새로운 태스크에 잘 적응하도록 도와줌

평가

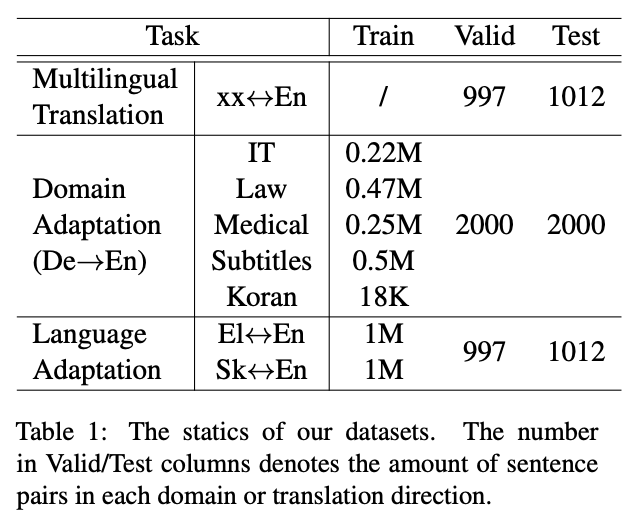
• 태스크
  • domain adaptation
  • language adaptation
• 모델
  • mBART5-nn
• 데이터셋
  • multilinguagl translation: FLORES-101
  • domain adaptation: OPUS (German -> English; IT, Law, Medical, Subtitles, Koran)
  • language adaptation: Greek <-> English, Slovak <-> English
• 평가지표
  • 4-gram case-sensitive BLEU (SacreBLEU tool)
  • SentencePiece BLEU

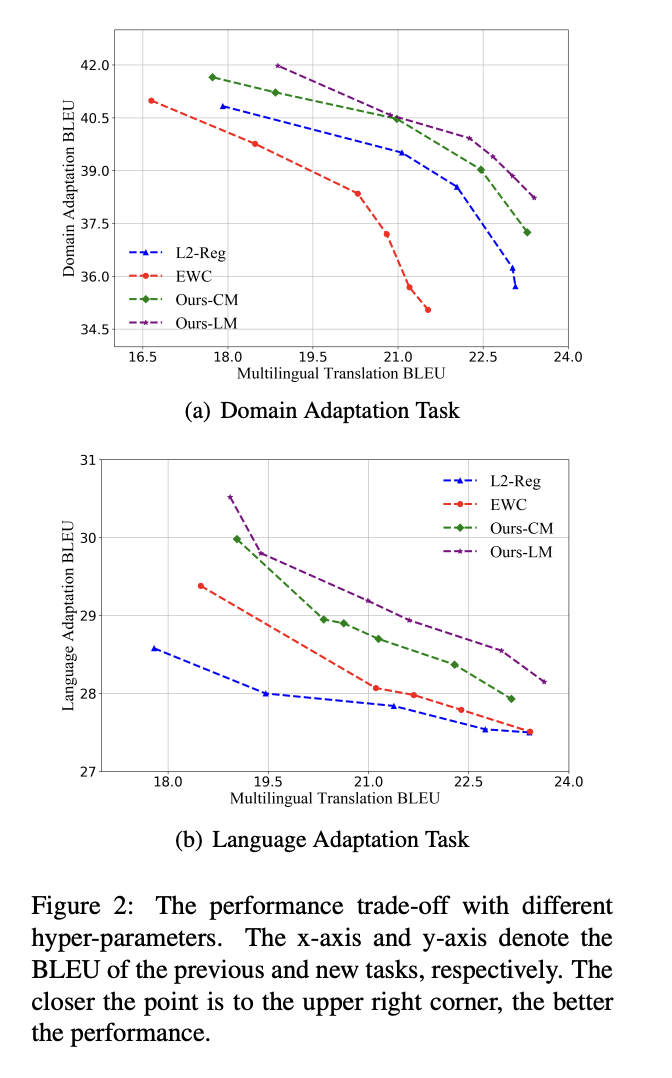
한계

• 연속학습에서 자주 사용되는 memory replay 방식이나 task-specific module(=model separation) 방식보다 성능이 떨어짐

의의

• 자신의 regularized-based 방식에 대한 다양한 실험
  • hyperparameter (loss의 비율을 결정) 튜닝보다 learning rate를 조절하는 것이 더욱 효과적
  • 이전의 데이터를 사용해 mixed training을 진행할 경우 오히려 성능이 떨어짐 (해당 regularization 방식과 memory replay는 함께 사용 불가)
  • sequential training에서 가장 좋은 성능
• 기존 L2-Reg, EWC와 같은 유명한 regularized-based 방식보다 좋은 성능
• 기존 Continual Learning과는 다소 다른 접근방식 (novelty)