1.3.3 Harmonically Related Complex Exponentials

eggmo·2024년 4월 13일

DSP

목록 보기

8/10

조화 신호라고 해야할까..?? 한국말 표현을 잘 모르겠다.

Harmonically Related Complex Exponentials은 정현파 신호의 기본 주파수의 정수배를 가지는 신호들을 말한다.

예를 들어 기본 주파수가 $\Omega_0$ 인 연속 시간 정현파 신호를 복소 지수 함수(Complex Exponentials) 형태로 표현하면 아래와 같다. (위상은 생략)

x(t) = e^{j(\Omega_0 t)}

즉 기본 주파수 $\Omega_0$ 의 정수배인 $k\Omega_0$ 를 가지는 정현파 신호들을 Harmonically Realted Complex Exponentials 라고 한다.
이를 식 [1.3.16]으로 표현할 수 있다.

s_k(t) = e^{j(k\Omega_0t)} = e^{j2\pi k F_0 t} \quad 단 \ k는 \ 정수\quad\quad\quad [1.3.16]

s_k(t) = Harmonically \ \ Complex \ \ \ Exponential

$s_k(t)$ 로 표현되는 정현파 신호의 기본 주파수는 $kF_0$ 이다. 연속 시간 정현파 신호에서 주파수의 범위는 실수 전체이기 때문에 다른 주파수를 가진 연속 시간 정현파 신호는 그 자체로 유일(구분)하다.

주의할 점은 기본 주파수와 Harmonically Related를 헷갈리면 안된다. 기본 주파수는 주기 신호를 시간 축에서 평행이동 하여 겹치게 만드는 값들 중 절댓값이 가장 작은 수를 의미한다. 반면 Harmonically는 특정 기본 주파수를 가진 신호와 그 기본 주파수의 정수배를 가지는 다른 신호와의 관계를 의미한다.

모든 연속 시간 신호는 기본 주파수 $f_0$ 를 가지는 정현파 신호와 Harmonically Related 된 신호의 합으로 표현이 가능하다. 이것을 푸리에 급수라고 한다. 이해가 안되면 [그림 1]을 참고해보자

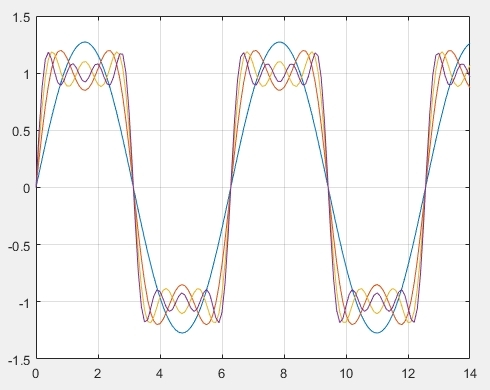
[그림 1]

[그림 1]에서는 사각 파형을 만들기 위해 수많은 정현파 신호를 더했다. 기본 주파수의 정현파 함수를 기반으로 Harmonically 관계에 있는 정현파 신호를 모두 더하여 원하는 신호를 만드는 것이다.

이를 식 [1.3.17]로 표현할 수 있다.

x_a(t) = \sum_{k=-\infty}^{\infty} c_ks_k(t) = \sum_{k=-\infty}^{\infty} c_ke^{j k\Omega_0t} \quad\quad\quad[1.3.17]

이 식에서 핵심은 $k\Omega_0$ 이다. $k =1$ 일 때는 기본 주파수 $\Omega_0$ 에 $c_1$ 의 가중치를 갖는 신호를, $k =2$ 일 때는 Harmonically 관계의 $2\Omega_0$ 에 $c_2$ 의 가중치를 가지는 신호를 쭉 더해 나가는 것이다. 복수 지수 함수로 표현되어 있기 때문에 익숙 하지 않다면 아래 식을 참고 해서 이해해 보자.

\sum_{k=-\infty}^{\infty} c_ke^{j2\pi k\Omega_0t} = \sum_{k=-\infty}^{\infty}c_k(cos(2\pi k\Omega_0t)+ jsin(2\pi k\Omega_0t))

이제는 명확히 확인할 수 있다. cos함수와 sin함수의 Harmonically 관계의 신호의 합을 통해 연속 시간 신호를 표현할 수 있는 것이다.

이산 시간 신호도 연속 시간 신호와 마찬가지로 Harmonically 관계의 신호의 합으로 표현이 가능하다.

이산 시간 신호의 기본 주파수를 $f_0$ 라고 하면 이 신호의 Harmonically 관계의 신호는 식 [1.3.18]로 표현이 가능하다.

s_k(n) = e^{j(k\Omega_0n)} = e^{j2\pi k f_0 n} \quad 단 \ k는 \ 정수\quad\quad\quad [1.3.18]

여기서 중요한 차이가 발생한다. 연속 시간 신호는 모든 주파수에 대해 유일하기 때문에 기본 주파수가 다르면 전부 다른 신호이다.

그러나 이산 시간 신호는 $-\pi <= w <= \pi$ 범위에서만 주파수가 유일하기 때문에 이 범위를 벗어나면 간섭(alias)가 일어난다.

따라서 $s_k(n) = s_{k+N}(n)$ 을 만족한다. 이해가 안되면 [그림 2]를 참고해보자.

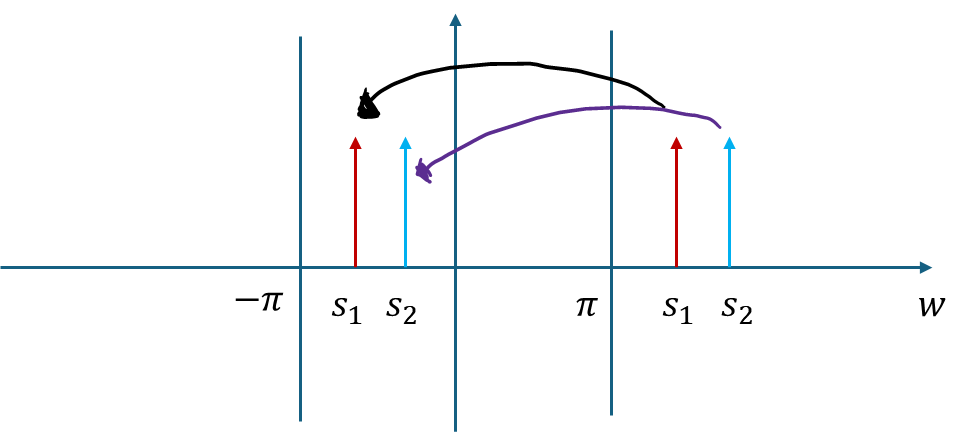
[그림 2]

[그림 2]에서 두 개의 빨간색 화살표와 두 개의 파란색 화살표는 $2\pi$ 만큼의 차이를 가지고 있다. 주파수가 $2\pi$ 차이가 난다는 것은 이산 시간 신호에서는 한 주기가 차이난다는 뜻이다. 이산 시간 신호의 주파수는 $-\pi <= w <= \pi$ 범위에서만 유일하기 때문에 이 범위 밖의 주파수는 간섭(Alias)가 일어난다.