1.4.1 Sampling of Analog Signals

샘플링(Sampling)이란 아날로그(연속 시간) 신호를 디지털(이산 시간) 신호로 바꾸는 과정을 말한다.

아날로그 신호는 시간축에 실수 전체에서 유효한데 이는 곧 값이 무한개라는 뜻이다. 컴퓨터는 무한개의 값을 처리할 수 없기 때문에 샘플링 과정을 통해 연속 시간 축을 이산 시간 축으로 바꿔야 한다.

이를 수식으로 표현하면 아래와 같다.

식을 해석해보면 연속 시간 신호의 시간축을 $T$ 초의 간격으로 선택하여 이산 시간 신호로 바꾸는 것이다. 누군가는 이렇게 질문할 수 있다.

"무한개의 연속 시간 값을 $T$ 간격으로 선택한다고 유한개가 되는 것은 아니지 않나요?"

이에 대한 답은 다음과 같다. 연속 시간 신호가 0~1초 사이에 있다면 0~1초 사이에도 무한개의 시간 값이 있다. 하지만 0~1초를 $T$의 간격으로 선택한다면

$\frac{1}{T}$ 개의 유한개의 시간 값이 있을 것이다. 이것이 연속 시간 신호를 이산 시간 신호로 바꾸는 샘플링이다.

이 때, $T$ 를 Sampling Frequency 로 정의하고 $\frac{1}{T}$ 를 Sampling Rate 로 정의한다.


따라서 연속 시간 축 $t$와 이산 시간 축 $n$은 [그림 1]과 같이 표현할 수 있다.

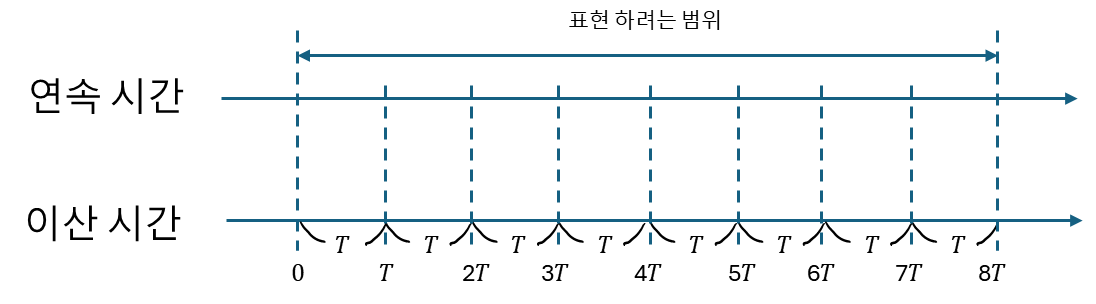
                                      [그림 1]

예를 들어 [그림 1]과 같은 상황일 때는 연속 시간 축은 실수 전체에서 정의 됐지만, 이산 시간으로 바뀔 때는 $nT$에 해당하는 축에서만 정의된다.
샘플링 주기 $T$의 역수는 샘플링 주파수 $F_s = \frac{1}{T}$이므로 식 [1,4,2]과 같이 쓸 수 있다.

연속 시간 축과 이산 시간 축의 관계를 이해하기 위해 식 [1,4,3]과 같은 연속 시간 정현파 함수가 있다고 가정하자.

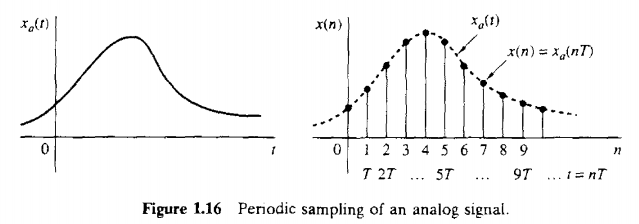
[그림 2] -출처 : Digital Signal Procesesing - Prokias

[그림 2]의 왼쪽 그림과 같이 연속 시간 축 $t$는 실수 전체에서 정의 되었지만, [그림 2]의 오른쪽 그림과 같이 샘플링 된 이 후, 연속 시간 축은 $nT$로 정의된다.

이를 식 [1,4,4]로 표현하면 아래와 같다.

연속 시간 신호는 $nT$ 에서만 정의되기 때문에 유한한 값이 되고 $x_a(nT)$ 이산 시간 신호이다. 그리고 구분을 위해 주기 $T$와 밑첨자 $a$를 생략하여

이산 신호인 $x(n)$으로 표현하게 된다.

연속 시간 신호의 기본 주파수와 이산 시간 신호의 기본 주파수의 사이의 관계도 정의할 수 있다.

이산 시간 신호의 기본 주파수 $f$는 식 [1,4,4]에서 $FT$ 이고 샘플링 주기 $T$는 샘플링 주파수 $\frac{1}{F_s}$의 역수와 같기 때문이다. 따라서 [식 1,4,5]가 유도된다.

1.3.2 장에서 연속 시간 주파수의 범위를 식 [1,4,7]로 정의한 적이 있다. (이해가 안되면 장 1,3,2 로 이동)

짧게 설명하면 연속 시간 신호의 기본 주파수가 다르면 신호 역시 다르다(구분된다) 라는 것이다.

그러나 이산 시간 신호는 기본 주파수가 $2 \pi$ 만큼 차이나면 간섭(Alias)가 일어난다. 따라서 이산 시간 신호의 주파수는 $2\pi$ 범위 내에서 정의 된다.

식으로 표현하면 [1,4,8]과 같다.

식 [1.4.5]를 식 [1.,4,8]에 대입하면 식 [1,4,9]가 만들어 진다.

식 [1.4.9]의 뜻은 연속 시간 신호를 샘플링 속도 $F_s$의 속도로 이산 시간 신호로 바꿀 때, 바꿀 수 있는 연속 시간 신호의 기본 주파수의 범위는 샘플링 주파수의 범위의 절반이라는 뜻이다.

이 뜻은 특정 샘플링 속도가 정해진다면 묘사할 수 있는 연속 시간 신호의 기본 주파수 범위는 제한된다는 점이다.

이해가 안간다면 아래 예시를 참고해보자.

위 두 신호가 있다. 샘플링 주파수 $F_s =40 Hz$ 로 설정했을 때 어떤 현상이 발생하는지 살펴보자.

샘플링 주파수가 정해졌으므로 연속 시간 신호를 이산 시간 신호로 바꿀 수 있다. 식 [1,4,5]를 통해 이산 시간 신호 식[1,4,13]을 만들 수 있다.

식에서 $x_1(n)$의 주파수는 10Hz이고 $x_2(n)$의 주파수는 50Hz임을 확인 가능하다.

이 때 $cos\frac{5\pi}{2} = cos\frac{\pi}{2}n$ 이므로 결국 $x_1(n)$ 과 $x_2(n)$은 같은 신호이다.

샘플링 주파수가 40Hz였기 때문에 묘사할 수 있는 연속 시간 주파수의 범위는 $-20 < F < 20$ 이고 50Hz는 해당 범위를 벗어났기 때문에 10Hz로 간섭(Alias)가 일어났다.

즉 이산 시간 신호 입장에서는 두 신호를 구분할 수 없다는 것이다. 그러므로 샘플링 과정은 모호성(Ambiguity)의 특징을 가지게 된다.

일반적으로 말하면 기본 주파수 $F_0$를 가지는 연속 시간 신호와, 기본 주파수 $F_0 + k F_s$ 를 가지는 연속 시간 신호는 이산 신호 관점에서 구분 할 수 없다.

모호성을 [그림 3]에서 잘 나타내주었다.

[그림 3] - 출처 : Digital Signal Procesing - Prokias

연속 시간 신호의 관점에서 두 신호는 구분 되지만, 이산 시간 신호 관점에서 두 신호는 구분되지 않는 것을 확인 할 수 있다.

식[1,4,9]를 다시 봐보자.

이를 바꿔서 표현하면 다음과 같다.

이 뜻은 만약 기본 주파수 $F$를 가진 연속 시간 신호를 샘플링하기 위해서는 기본 주파수의 2배 이상의 속도로 샘플링 주파수를 설정해야 한다는 것이다.

이것이 나이퀴스트 샘플링 이론이다. 바꿔 말하면 연속 시간 신호를 간섭(Alias)없이 이산 시간으로 묘사하기 위해 필요한 최소 샘플링 주파수를 식 [1,4,9]에서 확인할 수 있다.