4.1.2 Power Density Spectrum of Periodic Signals

eggmo·2024년 4월 17일

DSP

목록 보기

5/10

주기 신호(Periodic Signals)는 무한한 에너지를 가지고 유한한 평균 파워를 가진다.

주기 신호 $x(t)$ 에 대해 평균 파워는 식 [4.1.12]와 같이 구할 수 있다.

P_x = \frac{1}{T_p}\int_{T_p}^{}{\left\vert x(t)^2 \right\vert dt} \quad\quad\quad\quad [4.1.12]

주기 신호를 푸리에 급수로 표현하면 식 [4.1.12.1]과 같다.

x(t) =\sum_{k=-\infty}^{\infty}c_ke^{2\pi kF_0t} \quad\quad\quad\quad [4.1.12.1]

주기 신호 x(t)의 Power를 구하기 위해 식 [4.1.12.1]을 [4.1.12]에 대입하면 식 [4.1.13]로 전개할 수 있다.

P_x = \frac{1}{T_p}\int_{T_p}^{}{\left\vert x(t)^2 \right\vert dt}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad

= \frac{1}{T_p}\int_{T_p}x(t)\sum_{k=-\infty}^{\infty}c_k^{*}e^{-2\pi kF_0t}dt \quad\quad\quad\quad\quad\quad\quad

= \sum_{k=-\infty}^{\infty}c_k^{*}\frac{1}{T_p}\int_{T_p} x(t)e^{-2\pi kF_0t}dt \quad\quad\quad\quad [4.1.13]

추가로 설명하면 $x(t)$ 은 일반적으로 복소수(Comlex number)이므로 $x(t)$ 의 크기는 $\left\vert x(t)^2 \right\vert = x(t)x(t)^{*}$ 로 구할 수 있다.

식 [4.1.13]에서 $\sum_{k=-\infty}^{\infty}c_k^{*}e^{-2\pi kF_0t}$ 가 $x(t)^{*}$ 에 해당한다.

식 [4.1.13]에서 $\frac{1}{T_p}\int_{T_p} x(t)e^{-2\pi kF_0t}dt$ 는 푸리에 급수의 계수 $c_k$ 와 동일한 식이다. 따라서 식 [4.1.12]은 식[4.1.14]로 다시 쓸 수 있다.

P_x = \frac{1}{T_p}\int_{T_p}^{}{\left\vert x(t)^2 \right\vert dt} =\sum_{k=-\infty}^{\infty} \left\vert c_k\right\vert^{2} \quad\quad\quad\quad [4.1.14]

정리하면 주기 신호 $x(t)$ 의 Power는 주기 신호를 구성하는 Harmonically 신호의 푸리에 계수의 합이라는 뜻이다. 이것이 Parseval 정리이다.

예를 들어 주기 신호 $x(t) = c_ke^{j 2\pi k F_0t}$ 가 있다면 신호 $x(t)$ 의 평균 전력 $P_x$ 는 $\left\vert c_k \right\vert ^2$ 이다.

이 뜻을 명확하게 하기 위해 전력 밀도 스펙트럼을 [그림 1]과 같이 그려볼 수 있다.

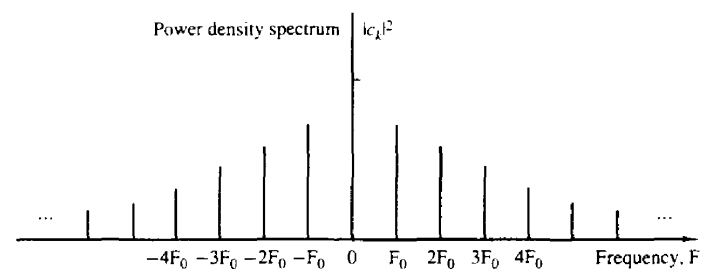
[그림 1]에서 x축은 주기 신호 $x(t)$ 를 구성하고 있는 Harmonically 함수 들의 주파수들을 나타낸 것이다. $F_0$ 는 신호 $x(t)$ 의 기본 주파수다.

[그림 1]의 y축은 푸리에 급수의 계수 크기이다. 각각의 Harmonically 주파수에 해당하는 푸리에 계수를 [그림 1]처럼 나타낼 수 있다.

이를 통해 주기 신호의 주파수 축 상에서 특징을 확인할 수 있다.

특징 중 하나는 주기 신호는 주파수(스펙트럼) 축 상에서 유한한(discrete) 값으로 존재한다. 주파수 축에서 Harmonically 관계의 주파수에서만 성분이 존재하고 나머지 주파수에서는 성분이 존재하지 않는다는 뜻이다. 이는 [그림 1]에서 확인할 수 있다.

그리고 인접한 주파수 성분의 간격은 주기 신호의 기본 주파수인 $F_0$ 이며 주기 $T_p$ 의 역수이다.

안녕하세요eggmo입니다.