4.1.2절에서는 주기 신호에 대한 푸리에 변환을 살펴보았다.
이번 장에서는 비주기 신호(Aperiodic Signal)에 대한 푸리에 변환을 알아 본다.
먼저 주기 함수에 대한 전력 밀도 스펙트럼을 [그림 1]처럼 나타낼 수 있다. 주기 신호의 주기 Tp가 클 수록 주파수 성분의 밀도가 빽빽해진다.
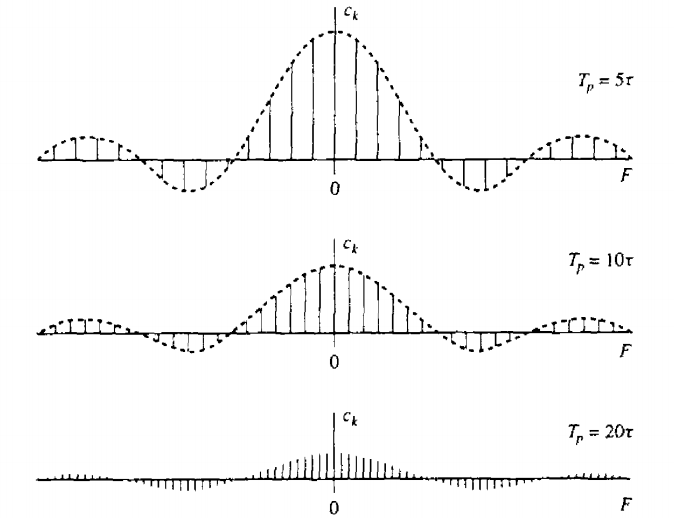
[그림 1]
만약 비주기 신호라면 어떻게 될까? 비주기 신호라면 주기 Tp=∞ 가 될 것이다. 그러면 기본 주파수 F0는 0 이다.
간격이 0이므로 전력 밀도 스펙트럼의 인접한 주파수 성분들은 연속하게 된다.
수식을 통해 비주기 함수와 주기함수의 관계를 푸리에 급수로 표현해보고 의미를 파악해보자.
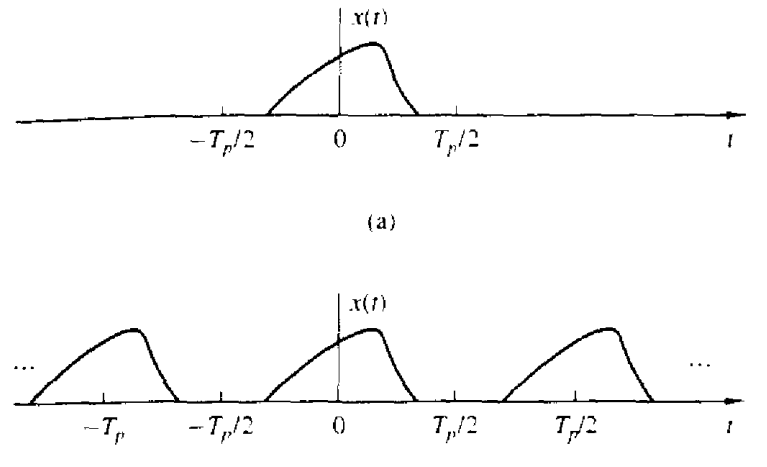
[그림 2]
[그림 2]의 위 신호는 비주기 신호 x(t)이고 [그림 2]의 아래 신호는 주기가 Tp인 주기 신호 xp(t)이다. (그림에서 Tp/2가 두번 나오는 건 오류)
주기 신호 xp(t)의 주기 Tp를 무한대로 보내면 비주기 함수가 되어 [그림 2]의 위 신호와 같아지게 된다.
주기 신호 xp(t)를 푸리에 급수로 나타내면 식[4.1.20], 식[4.1.21]과 같다.
xp(t)=k=−∞∑∞ckej2πkF0t[4.1.20]
ck=Tp1∫−Tp/2Tp/2xp(t)e−j2πkF0tdt[4.1.21]
을 만족한다.
비주기 신호 x(t)는 −2Tp<=t<=2Tp 에서 주기 신호 xp(t)와 같다. 따라서 주기 신호 x(t)를 푸리에 급수로 나타내면 식 [4.1.22]와 같다.
ck=Tp1∫−Tp/2Tp/2x(t)e−j2πkF0tdt[4.1.22]
이 때 비주기 신호 x(t)는 −2Tp<=t<=2Tp 범위 밖에서 값이 0이기 때문에 식 [4.1.22]의 적분 구간을 무한대로 확장할 수 있다. 즉 식 [4.1.23]과 같다.
ck=Tp1∫−∞∞x(t)e−j2πkF0tdt[4.1.23]
∫−∞∞x(t)e−j2πkF0tdt 를 X(kF)로 정의해보자. 이것이 주기함수의 푸리에 급수이다. 그러면 [식 4.1.24]가 된다.
X(kF0)=∫−∞∞x(t)e−j2πkF0tdt[4.1.24]
식 [4.1.23]과 식 [4.1.24]를 결합하면 식 [4.1.25]가 만들어 진다.
Tpck=X(kF0)=X(Tpk)[4.1.25]
식 [4.1.25]를 통해 xp(t)의 푸리에 변환 X(kF0)는 주파수 축에서 인접한 주파수 간격이 F0임을 확인할 수 있다. 즉 유한하다.
만약 주기 Tp가 무한대로 가면 주기 신호는 비주기 신호가 되고 주파수 축에서 인접한 주파수 간격이 0이 됨을 확인할 수 있다. 즉 연속한다.
만약 식 [4.1.20]과 식 식 [4.1.25]를 결합하면 식 [4.1.26]과 같다.
xp(t)=Tp1k=−∞∑∞X(Tpk)ej2πkF0t[4.1.26]
즉 푸리에 변환식에 ej2πkF0t 를 곱해주면 주파수축 신호가 시간축 신호로 바뀜을 확인할 수 있다. 이것이 주기 함수의 역 푸리에급수(Inverse-Fourier Series) 이다.
정리하자면 식 [4.1.24]에서 처럼 시간축 함수 x(t)에 e−j2πkF0t를 곱해 주파수 축 함수 X(kF)로 바꾸는 과정을 푸리에 변환이라고 한다.
반대로 식 [4.1.26] 처럼 주파수 축 함수 X(kTp)=X(F0k) 를 시간축 함수 x(t)로 바꾸는 과정을 역푸리에 변환이라고 하는 것이다.
추가로 kF0가 0으로 가면 주기함수가 비주기 함수가 되고 유한한 값인 kF0가 연속인 값인 F가 된다. 따라서 역 푸리에변환은 식[4.1.27]과 같이 다시 쓸 수 있다.
x(t)=Tp1k=−∞∑∞X(F)ej2πFt[4.1.27]
식 [4.1.27]은 비주기함수의 푸리에 급수이며 비주기함수의 푸리에 변환이다.
식 [4.1.24]에서 유한한 주파수 축인 kF0를 무한한 주파수 축인 F로 바꾸면 식 [4.1.28]과 같다.
X(F)=∫−∞∞x(t)e−j2πFtdt[4.1.28]
식 [4.1.28]은 비주기함수의 푸리에 급수이며 비주기함수의 푸리에 변환이다.
이를 통해 푸리에 급수는 주기 신호에 대한 푸리에 급수이고 푸리에 변환은 비주기 신호에 대한 푸리에 급수인 것을 알 수 있다. 바꿔 말하면 유한한 주파수 축을 무한한 주파수 축으로 확장한 것이고 주기 신호에서 정의된 푸리에 급수를 비주기 신호로 확장한 것이다.
마지막으로 주파수를 각주파수로 바꿔서 표현하면 푸리에 변환은 식 [4.1.31], 식 [4.1.32]과 같다.
x(t)=2π1∫−∞∞X(Ω)ejΩtdΩ[4.1.31]
x(Ω)=∫−∞∞x(t)e−jΩtdt[4.1.32]
[그림 1]과 비교해서 설명하면 시간축에서 비주기 신호의 주파수 스펙트럼 성분을 구하는 것이 식 [4.1.32]에 해당하고 주파수 축에서 비주기 함수의 시간 축 신호를 구하는 것이 식 [4.1.31]이다.

