About VAE

kangmin·2024년 9월 17일

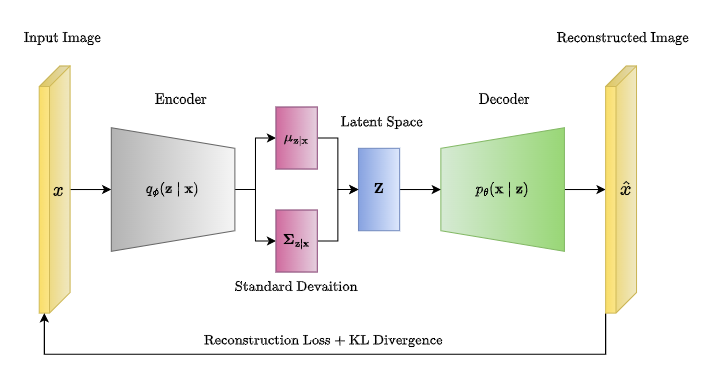
VAE는 Variational Auto Encoder의 약자로 오토인코더의 확장된 형태로, 확률적 접근을 통하여 더 의미 있는 잠재 공간 표현을 학습합니다.

따라서 VAE를 학습하기 이전에 Auto Encoder에 대해 먼저 알아봅시다.

Auto Encoder

오토인코더의 정의는 자체 입력 데이터를 재구성하도록 비지도 학습을 통해 훈련된 인코더-디코더 아키텍처의 하위 집합입니다.

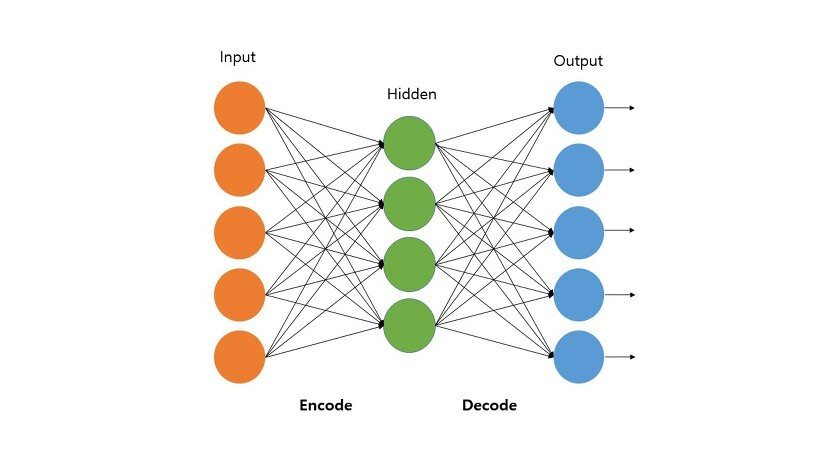
위 이미지는 오토인코더의 기본 구조를 나타냅니다.

입력 데이터를 전달 받음
인코더에서 특징을 추출함
디코더에서 해당 특징을 바탕으로 입력 데이터를 복호화함

해당 부분을 수식으로 표현하자면 다음과 같습니다.

$z = h(x)$

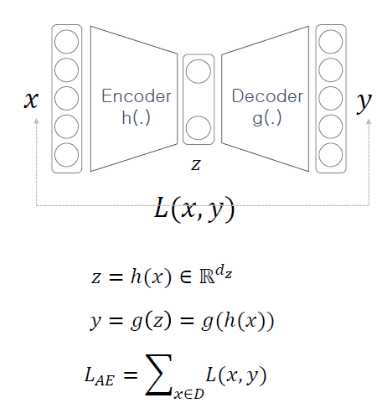
z : latent variable
h() : encoder function
x : input data

$y = g(z) = g(h(x))$

y : output data
g() : decoder function

$L_{AE} = \sum L(x,y)$

$L_{AE}$ : sum of loss function
L(x,y) : difference detween x and y

따라서 정리하자면 오토인코더는 입력 데이터를 받아 특징을 추출하고 해당 특징을 바탕으로 결과를 출력합니다.

Variational Auto Encoder

VAE는 위 오토인코더의 Latent Space로 부터 데이터를 생성하자는 점에서 출발하였습니다.

VAE의 작동 방식은 입력 데이터를 받으면 encoder를 통하여 평균과 표준편차를 출력합니다.
이후 만들어진 정규 분포로부터 샘플링을 통해 latent variable을 생성한 후 decoder를 통해 입력된 데이터의 분포로 매핑되어 새로운 데이터를 추정할 수 있습니다.

encoder 작동 방식

gausian encoder를 거쳐 평균, 표준편차 반환

$\mu(x), \log \sigma^2(x) = f_{\text{encoder}}(x)$

잠재변수 z 샘플링

$z = \mu(x) + \sigma(x) \odot \epsilon$

$\epsilon$ 은 표준 정규 분포에서 샘플링된 노이즈로 해당 방법을 reparameterization trick라고 부르며 샘플링 과정을 미분 가능하게 만들기 위해 사용됩니다.

decoder 작동 방식

decoder는 z로 부터 x를 생성하는 조건부 확률을 학습합니다.

loss function

VAE의 전체 손실함수는 재구성 손실과 KL 발산의 조합입니다.

$\mathcal{L}_{\text{VAE}} = \mathcal{L}_{\text{reconstruction}} + \beta D_{\text{KL}}(q(z|x) \parallel p(z))$

재구성 손실

재구성 손실이란 원본 데이터가 디코더로 생성된 데이터간의 차이를 의미합니다.

수식

$\text{Reconstruction Loss} = \mathbb{E}_{q(z|x)}[-\log p(x|z)]$

구현 방식

연속형 데이터 $\mathcal{L}_{\text{reconstruction}} = \frac{1}{N} \sum_{i=1}^{N} (x_i - x'_i)^2$
이진 데이터 $\mathcal{L}_{\text{reconstruction}} = - \sum_{i} \left[ x_i \log(x'_i) + (1 - x_i) \log(1 - x'_i) \right]$

KL 발산

KL 발산은 인코더가 생성한 잠재 변수의 분포와 사전 분포간의 차이를 측정합니다.

사전분포는 파라미터가 관측되기 전에 미리 가정하는 확률 분포를 의미하며 값의 범위나 특성에 대한 사전 지식을 반영합니다. VAE에서는 표준 정규 분포를 사전 분포로 설정합니다.

정의

$D_{\text{KL}}(q(z|x) \parallel p(z)) = \mathbb{E}_{q(z|x)} \left[ \log \frac{p(z)}{q(z|x)} \right]$
```
	q(z∣x): 인코더가 학습한 잠재 변수 z의 분포
	p(z): 사전 분포 
```