통계 (3)

Chapter1 기초통계_기초과정

6) 추정

1. 추정

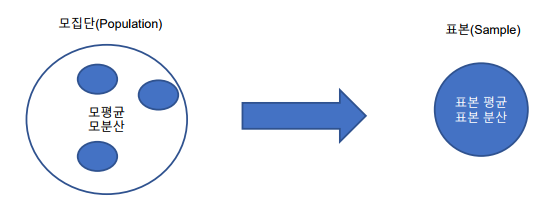
• 추정(estimation): 모집단의 모수를 모를 경우 표본으로 추출된 통계량을 모집단의 근사값으로 사용하는 것

• 추정량(estimator): 표본 평균으로 모평균을 추정할 때 표본 평균을 모평균에 대한 추정량이라고 함

• 점추정(point estimation): 모수를 하나의 특정값으로 추정 하는 방법

• 구간추정(interval estimation): 모수가 포함될 수 있는 구간을 추정하는 방법
  

점추정의 성질

• 일치성(Consisttency): 표본의 크기가 모집단의 크기에 근접해야 함, 표본의 크기가 클수록 추정량의 오차가 작아짐

• 불편성(unbiased estimator): 추정량이 모수와 같아야 함

• 유효성(efficiency): 추정량의 분산이 최소값이어야 함

• 평균오차제곰(MSE): 평균오차제곱이 최소값이어야 함

• 구간추정: 모수가 포함될 수 있는 구간을 추정하는 방법

• 신뢰구간(confidence level): 추정값이 존재하는 구간에 모수가 포함될 확률
  -> 신뢰 수준은 100 * (1-a)% 로 계산 하며, a는 오차 수준
  -> 신뢰 수준 95%라는 것은 구간 추정된 값의 오차가 발생할 확률이 5%라는 것을 의미
  -> 이 오차를 유의 수준(significant level)이라고 하며, p = 0.05라고 함

• 신뢰구간은 신뢰 하한, 신뢰 상한으로 표시

  $P\left( L(\hat{\theta}) \leq \theta \leq U(\hat{\theta}) \right) = 1 - \alpha$

표본의 크기 결정
-> 허용오차(permissible error): 추정한 값이 틀려도 허용할 수 있는 오차
-> 정규분포의 신뢰구간을 통해 허용 오차를 계산

2. 모비율 추정

• 모비율의 점추정: 비율에 대한 추정으로 우리가 원하는 속성(class)에 속하면 1 아니면 0일때, 1의 속성을 갖는 것의 개수를 X라고 하면 X ~ B(n,p)임, 이때 모비율의 점추정량을 표본 비율이라고 함
  $E(\hat{p}) = E\left(\frac{X}{n}\right) = \frac{np}{n} = p,$

• 모비율의 구간 추정
• 모비율 구간 추정에서 정규분포의 근사가 가능한 대표본은 보통 np > 5, n(1-p) >5를 동시에 만족 해야 함
  $P(-z_{\frac{\alpha}{2}} \leq Z \leq z_{\frac{\alpha}{2}}) = 1 - \alpha \implies P\left(-z_{\frac{\alpha}{2}} \leq \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}} \leq z_{\frac{\alpha}{2}}\right) = P\left(-z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{p(1-p)}{n}} \leq \hat{p} - p \leq z_{\frac{\alpha}{2}} \cdot \sqrt{\frac{p(1-p)}{n}}\right).$

• 모평균 차이의 추정(점추정)
  $E(\overline{X}_1 - \overline{X}_2) = E(\overline{X}_1) - E(\overline{X}_2) = \mu_1 - \mu_2$

• 모평균 차이의 추정(구간추정: 대표본)
  $Z = \frac{(\overline{X}_1-\overline{X}_2)-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}} \sim N(0,1) \Rightarrow 1 - \alpha = P(-z_{\frac{\alpha}{2}} < Z < z_{\frac{\alpha}{2}}) = P\left(-z_{\frac{\alpha}{2}} < \frac{(\overline{X}_1-\overline{X}_2)-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}} < z_{\frac{\alpha}{2}}\right)$

• 모평균 차이의 추정(구간추정: 소표본, 모분산을 모르는 경우)
  -> 두 모집단의 분산을 모르는 경우에는 등분산 가정이 필요

• 합동 분산 추정량(pooled variance estimator)
  $s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}$

• 모비율 차이의 추정(점추정)
  $E(\hat{p}_1 - \hat{p}_2) = E(\hat{p}_1) - E(\hat{p}_2) = p_1 - p_2$

• 모비율 차이의 추정(구간추정)
  $\frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \sim Z(0,1) \implies 1 - \alpha = P\left(-z_{\frac{\alpha}{2}} < Z < z_{\frac{\alpha}{2}}\right) = P\left(-z_{\frac{\alpha}{2}} < \frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} < z_{\frac{\alpha}{2}}\right)$

Chapter2 기초통계_심화과정

7) 가설 검정

1. 가설검정과 유의수준 정의

• 가설 검정 = 가설(Hypothesis) + 검정(Testing)

• 가설(Hypothesis): 주어진 사실 또는 조사하려고 하는 사실에 대한 주장 또는 추축

• 통계학에서는 특히 모수를 추정 할 때 모수가 어떠하다는 증명을 하고 싶은 추축이나 주장을 가설이라고 함 할 때 모수가 어떠하다는 증명을 하고 싶은 추축이나 주장을 가설이라고 함

• 귀무가설(Null hypothesis: $H_0$): 기존의 사실, 대립가설과 반대되는 가설로 연구목적이 아님

• 대립가설(Alternative hypothesis: $H_1$): 데이터로부터 나온 주장하고 싶은 가설 또는 연구의 목적으로 귀무가설의 반대

• 제1종 오류: 귀무가설이 참이지만, 귀무가설을 기각하는 오류
  -> 제1종 오류를 범할 확률의 최대허용 한계를 유의수준이라고 하며, 알파로 표시

• 제2종 오류: 귀무가설을 기각해야 하지만, 귀무가설을 채택하는 오류

• 검정통계량: 귀무가설이 참이라는 가정하에 얻은 통계량
  -> 검정결과 대립가설을 선택하게 되면 귀무가설을 기가함
  -> 검정결과 귀무가설을 선택하게 되면 귀무가설을 기각하지 못한다고 표현함

• P-value: 귀무가설이 참일 확률로 0~1 사이의 표준화된 지표

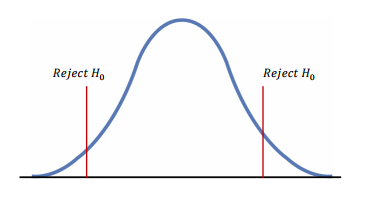
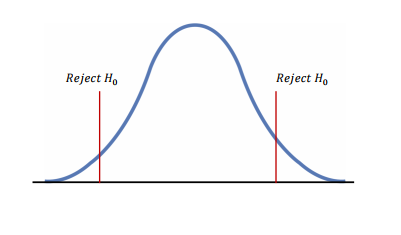
• 기각역(reject region): 귀무가설을 기각시키는 검정통계량의 관측값의 영역

가설 검정의 절차
1. 가설수립
2. 유의 수준 결정
3. 기각역 설정
4. 검정통계량 계산
5. 의사결정

• 양측검정(two-side test): 대립가설의 내용이 같지 않다 또는 차이가 있다 등의 양쪽 방향의 주장
• 단측검정(one-side test): 한쪽만 검증하는 방식으로 대립가설의 내용이 크다 또는 작다 처럼 한쪽 방향의 주장

2. 단일 표본에 대한 가설검정

• 모평균 가설검정 - 모분산을 아는 경우

가설:
a) 귀무 가설 $H_0: \mu = \mu_0$ vs 대립 가설 $H_1: \mu \neq \mu_0$
b) 귀무 가설 $H_0: \mu = \mu_0$ vs 대립 가설 $H_1: \mu > \mu_0$
c) 귀무 가설 $H_0: \mu = \mu_0$ vs 대립 가설 $H_1: \mu < \mu_0$

유의수준:
$\alpha = 0.05$, 검정통계량: $z = \frac{\overline{x} - \mu}{\sigma/\sqrt{n}} \sim N(0,1)$

검정통계량 관측값:
$z_0 = \frac{\overline{x} - \mu_0}{\sigma/\sqrt{n}}$

a) $|z_0| \geq z_{\alpha/2}$ 이면 $H_0$ 기각
b) $z_0 \geq z_{\alpha}$ 이면 $H_0$ 기각
c) $z_0 \leq -z_{\alpha}$ 이면 $H_0$ 기각

• 모평균 가설검정 - 모분산을 모르는 경우(소표본)

가설:
a) $H_0: \mu = \mu_0$ vs $H_1: \mu \neq \mu_0$
b) $H_0: \mu = \mu_0$ vs $H_1: \mu > \mu_0$
c) $H_0: \mu = \mu_0$ vs $H_1: \mu < \mu_0$

유의수준:
$\alpha = 0.05$, 검정통계량: $T = \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim t(n-1)$

검정통계량 관측값:
$t_0 = \frac{\overline{X} - \mu_0}{\sigma/\sqrt{n}}$

a) $|t_0| \geq t_{\alpha/2}(n-1)$ 이면 $H_0$ 기각
b) $t_0 \geq t_{\alpha}(n-1)$ 이면 $H_0$ 기각
c) $t_0 \leq -t_{\alpha}(n-1)$ 이면 $H_0$ 기각

3. 두개의 표본에 대한 가설 검정

• 대표본 - 모분산을 아는 경우

가설:
a) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 \neq \mu_2$
b) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 > \mu_2$
c) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 < \mu_2$

유의수준:
$\alpha = 0.05$, 검정통계량: $Z = \frac{(\overline{X}_1 - \overline{X}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} \sim N(0,1)$

검정통계량 관측값:
$Z_0 = \frac{(\overline{X}_1 - \overline{X}_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}$

a) $|Z_0| \geq Z_{\alpha/2}$ 이면 $H_0$ 기각
b) $Z_0 \geq Z_{\alpha}$ 이면 $H_0$ 기각
c) $Z_0 \leq -Z_{\alpha}$ 이면 $H_0$ 기각

• 소표본 - 모분산을 모르는 경우

가설:
a) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 \neq \mu_2$
b) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 > \mu_2$
c) $H_0: \mu_1 = \mu_2$ vs $H_1: \mu_1 < \mu_2$

유의수준:
$\alpha = 0.05$, $S_p^2 = \frac{(n_1-1)S_1^2 + (n_2-1)S_2^2}{n_1 + n_2 - 2}$, 검정통계량: $T = \frac{(\overline{X}_1 - \overline{X}_2) - (\mu_1 - \mu_2)}{S_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)$

검정통계량 관측값:
$T_0 = \frac{(\overline{X}_1 - \overline{X}_2)}{S_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}$

a) $|T_0| \geq t_{\alpha/2}(n_1 + n_2 - 2)$ 이면 $H_0$ 기각
b) $T_0 \geq t_{\alpha}(n_1 + n_2 - 2)$ 이면 $H_0$ 기각
c) $T_0 \leq -t_{\alpha}(n_1 + n_2 - 2)$ 이면 $H_0$ 기각

• 대응 비교: 쌍으로 조사된 자료 $(X_1, Y_1), (X_2, Y_2), ..., (X_l, Y_l)$가 주어졌을 때, $X_i$의 평균을 $\mu_X$, $Y_i$의 평균을 $\mu_Y$라고 하면, $D_i = X_i - Y_i$로 정의함

가설:
a) $H_0: \mu_X = \mu_Y$ vs $H_1: \mu_X \neq \mu_Y$
b) $H_0: \mu_X = \mu_Y$ vs $H_1: \mu_X > \mu_Y$
c) $H_0: \mu_X = \mu_Y$ vs $H_1: \mu_X < \mu_Y$

a) $H_0: \mu_D = 0$ vs $H_1: \mu_D \neq 0$
b) $H_0: \mu_D = 0$ vs $H_1: \mu_D > 0$
c) $H_0: \mu_D = 0$ vs $H_1: \mu_D < 0$

유의수준:
$\alpha = 0.05$, 검정통계량: $T = \frac{\overline{D} - \mu_D}{S_D / \sqrt{n}} \sim t(n-1)$

검정통계량 관측값:
$T_0 = \frac{\overline{D} - \mu_D}{S_D / \sqrt{n}}$

a) $|t_0| \geq t_{\alpha/2}$ 이면 $H_0$ 기각
b) $t_0 \geq t_{\alpha}$ 이면 $H_0$ 기각
c) $t_0 \leq -t_{\alpha}$ 이면 $H_0$ 기각

이 글은 제로베이스 강의 자료 일부를 발췌하여 작성되었습니다