Ian J.Goodfellow 의 논문 (2014)

Abstract

• 데이터 분포를 생성하는 generative model G 와 그 데이터 분포를 판별하는 discriminative model D를 통해 두 가지 모델을 동시에 훈련하는 적대적 프로세스를 통해 생성 모델을 추정하기 위한 새로운 프레임 워크를 제안
• G는 training 과정에서 D가 실수할 확률을 최대화 한다
• G와 D의 고유한 해는 존재한다 (G는 training data를 재현하고 D는 1/2 을 출력)
• G와 D는 다층 퍼셉트론으로 정의되고 backpropagation으로 훈련된다
• 실험을 통해 질적, 정량적 평가를 통한 프레임워크의 잠재력을 입증함

1 Introduction

• 딥러닝은 인공지능이 마주하는 자연 이미지, 음성을 포함하는 오디오 파형 및 자연어 기호와 같은 데이터의 풍부한 확률 분포를 포함하는 계층적 모델을 발견하는 것이다
• 지금까지 딥러닝에서 가장 두드러진 성공은 고차원적이고 풍부한 입력을 클래스 레이블에 매핑하는 discriminative models과 관련있다(이러한 성공은 backpropagation과 dropout 알고리즘 덕분)
• 심층 생성모델은 다루기 힘든 확률적인 계산을 근사하는 것의 어려움과 generative context에서 piecewise linear units이용하는 것에 어려움이 있다
• 논문에서는 이러한 어려움을 피하는 새로운 생성모델을 제안
• 논문에서 제안한 advesarial nets framework에서 generative model은 적과 대립한다
• discriminative model은 데이터가 모델의 분포인지, 진짜 데이터의 분포인지 결정하도록 학습한다
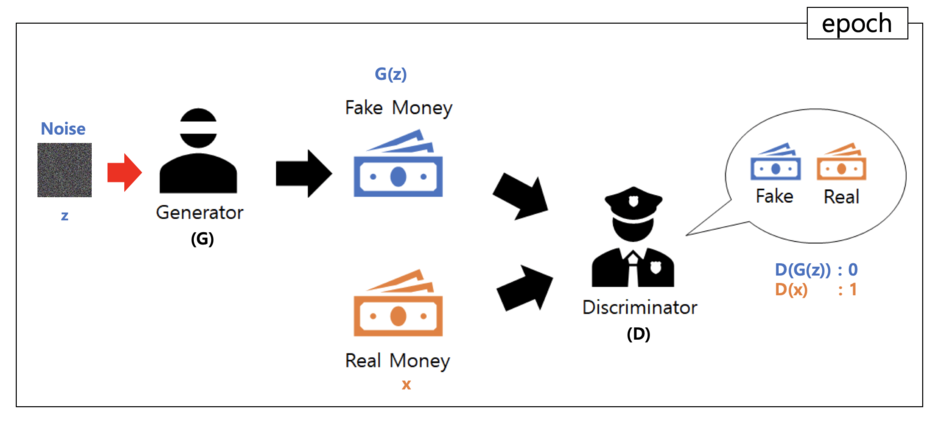
• generative model은 가짜 지폐를 생산하여 탐지되지 않도록 노력하는 위조범과 유사하다고 생각할 수 있고, discriminative model은 위조 지폐를 탐지하려는 경찰과 유시하다고 생각할 수 있다
• 이 게임의 경쟁은 위조품을 진짜와 가짜로 구별할 수 없을 때까지 두 팀(G와 D)가 그들의 방법을 개선하도록 한다
• 본 논문에서는 G가 다층 퍼셉트론에 랜덤 노이즈를 통과시켜 샘플을 생성하는 경우를 살펴보고 D 역시 다층 퍼셉트론이다
• 역전파 및 드롭아웃 알고리즘만을 사용해 두 모델을 훈련하고 샘플을 생성하는 경우 G의 순전파를 사용해 생성한다
  

2 Relative work

생략

3 Adversarial nets

• 모델이 모두 다층 퍼셉트론인 경우 적대적 모델링 프레임워크를 가장 쉽게 적용할 수 있다
• 데이터 x에 대한 확률분포 pg를 학습하기위해 사전 입력 노이즈 변수 pz(z)를 정의하고 데이터 공간에 대한 매핑을 G(z;θ)로 표현한다(G는 매개 변수 θg를 갖는 다층 퍼셉트론으로 미분가능한 함수이다)
• 또한 단일 스칼라값을 출력하는 두 번째 다층 퍼셉트론 D(x; θd)를 정의한다
• D(x)는 pg가 아닌 데이터에서 x가 나왔을 확률울 나타낸다
• D가 training example과 G의 sample 모두에 정확한 레이블을 할당할 확률을 최대화 하도록 D를 훈련한다
• 동시에 G를 훈련하여 log(1 - D(G(z))를 최소화한다
• 즉, D와 G는 함수 V(G, D)로 2인용 minmax game을 한다

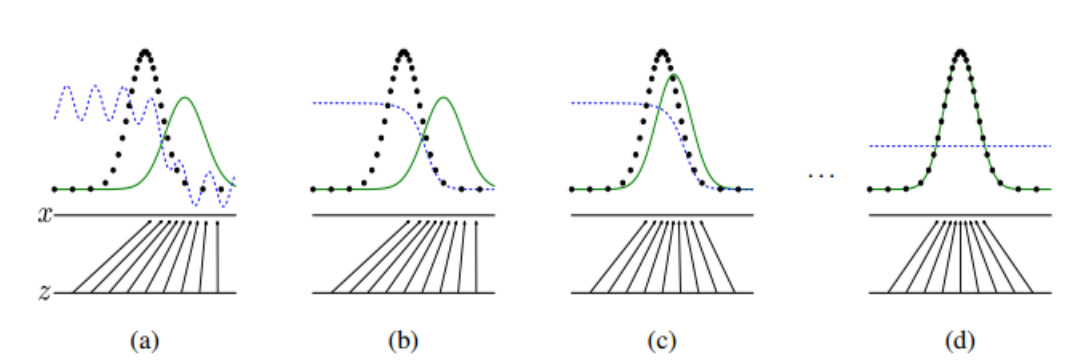
• 파란 점선은 D의 판별분포, 녹색 실선은 G의 데이터 생성분포, 검정 점선은 실제 데이터의 분포, 아래의 수평선은 z가 샘플링되는 분포
• (b)를 보면 D가 inner loop를 돌며 훈련되면 real 데이터의 경우 잘 맞추는 걸 알 수 있다
• (c), (d)에서 G가 노이즈 z에서 실제 데이터와 비슷하게 분포를 맵핑하도록 훈련해
  D는 그 둘을 잘 구별하지 못해서 0.5와 비슷한 확률분포를 출력한다

• 두 모델을 모두 훈련시키며 D를 최적화하는것은 계산상 불가능하다

• 그 대신에 본 논문에서는 D를 최적화하는 k 단계와 G를 최적화하는 한 단계를 교대로 한다

• 결과적으로 D는 최적해 근처로 최적화 할 수 있고, G도 천천히 변하면서 최적화 할 수 있다

• 실제로 위의 식 (1)에서 G가 잘 학습되지 않을 수 있다

• 학습 초기에 G의 성능은 좋지 못하고, D는 성능이 좋지 않은 G에 대해서 training data와 많이 다르기 때문에 위조 데이터를 모두 판별하기 때문

• 그래서 G를 log(1 − D(G(z )))를 최소화하기 보단, log D(G(z ))를 최대화 하도록 훈련

4 Theoretical Results

• 모델이 어떻게 전역최적해로 어떻게 수렴하는지 설명

4.1 Global Optimality of pg = pdata

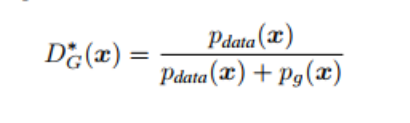
• G를 고정시키면 D의 최적해는 위와 같다고 한다
• 증명
  

  • V(G, D)의 expectation을 적분으로 펼치면 위와 같은 식으로 나타 낼 수 있다
  • pdata(x)를 a, pz(z)를 b, D(x)를 y 라고 하면 위 식은 alog(y) + blog(1-y)로 변환됨
  • [0, 1] y의 최대값은 a/(a+b) 이다 따라서 D(x)의 최적해는 식 (2)과 같다

• 이번에는 전역최적해가 pg = pdata 임을 증명
  

  • C(G)라는 함수를 D에 대한 V(G, D)를 최대로 하는 함수로 정의
  • 위에서 구한 식을 바탕으로 D(x)를 치환 할 수 있다
  • 그리고 그 식은 분자에 2를 곱하고 log(4)를 빼준 것과 같다
  • 이 식을 KL divergence로 변환(두 확률분포의 차이를 계산하는 함수)
  • 그리고 이 식을 JSD()로 바꿀 수 있다
  • 이 JSD가 최소가 되는 해는 pdata = pg 이므로 pdata = pg일 때 함수 C(G)가 전역최적해를 갖는다(그때 C(g) 값은 -log(4))

5 Experiments

• MNIST, TFD(얼굴 데이터셋), CIFAT-10 데이터 셋을 활용해 GAN을 학습시킴
• generator nets는 Relu와 sigmoid 활성화함수를, discriminator net은 maxout 활성화 함수를 사용함
• Dropout이 discriminator net 훈련에 사용되었다
• noise는 generator의 가장 하위 layer에만 인풋으로 사용되었다
  

• 가장 오른쪽 열은 생성한 이미지이다 이것은 생성 이미지가 training 데이터를 완전히 따라하지 않음을 보여준다
• 다른 오토인코더 계열 생성형 모델보다 GAN이 좀 더 블러하지 않고 샤프하다

6 Advantages and disadvantages

• GAN은 이전의 모델들에 비해 장단점이 있다
• 단점
  • pg(x)의 명시적인 표현이 없다는 것과 D를 훈련 중 G와 잘 동기화되어야 한다
• 장점
  • 마르코프 체인이 필요하지 않고 역전파만 그레이디언트를 얻는데 사용
  • 다양한 함수를 모델에 통합할 수 있다
  • 마르코프 체인을 기반으로 한 모델은 다소 흐릿한 이미지를 생성하지만 GAN은 그렇지 않다