ML-review 차원 축소

차원 축소

• 일반적으로 차원이 증가 할수록 데이터가 sparse한 구조를 가지게 된다
• 피처가 많을 경우 개별 피처간에 상관관계가 높을 가능성이 있어 선형 회귀와 같은 선형 모델에서는 다중 공산성 문제로 모델 성능이 저하 될 수 있다
• 피처 선택(feature selection): 특정 피처에 종속성이 강한 불필요한 피처를 아예 제거
• 피처 추출(feature extraction): 기존 피처를 저차원의 중요 피처로 압축해서 추출
• 차원 축소는 기존 피처가 전혀 인지하기 어려웠던 잠재적인 요소(Latent Factor)를 추출하는 것을 의미한다
• 매우 많은 픽셀로 이루어진 이미지 데이터에서 잠재된 특성을 피처로 도출해 훨씬 작은 차원으로 바꿔서 과적합 영향력이 작아져서 오히려 원본 데이터보다 예측 성능을 올릴 수 있다
• 텍스트 문서에서 차원 축소를 통해 시멘틱(Semantic)의미나 토픽(Topic)을 잠재 요소로 간주하고 이를 찾아 낼 수 있다

1 PCA(Principal Component Analysis)

• 주성분(Principal Component)를 추출해 차원을 축소하는 기법
• PCA는 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소한다 → 이 축이 주성분

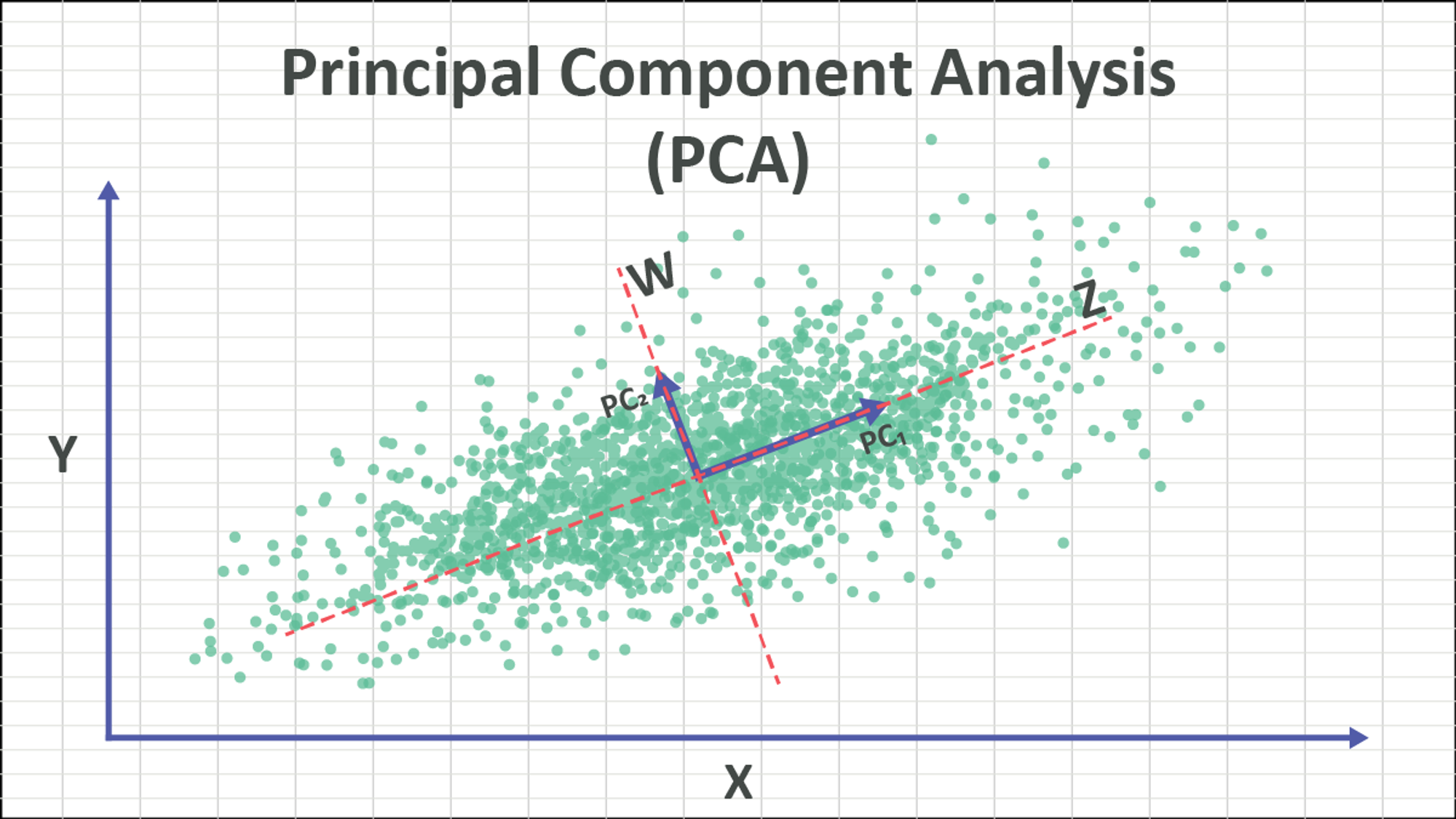
• PCA는 먼저 가장 큰 변동성(Variance)를 기반으로 첫 번째 축을 생성하고 두 번째 축은 이 벡터 축에 직각이 되는 벡터를 축으로 한다
• PCA의 과정은 데이터의 공분산 행렬을 고유값 분해하고 → 이렇게 구한 고유벡터에 입력 데이터를 선형 변환한다

	X	Y	Z
X	3.0	-0.71	-0.24
Y	-0.71	4.5	0.28
Z	-0.24	0.28	0.91

• 공분산 행렬이 위와 같을 때 대각 성분의 값은 각 피처의 분산이고 공분산 Cov(X, Y) < 0이므로 서로 X와 Y는 서로 반비례관계이다
• 위의 공분산 행렬을 C라고 하면 아래와 같이 고유값 분해 할 수 있다

• $e_1$이 가장 분산이 큰 고유 벡터이다
• 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식이 PCA이다

2 LDA(Linear Discriminant Analysis)

• LDA는 PCA와 유사하나 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소
• LDA는 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화 하는 방식으로 차원 축소한다
  

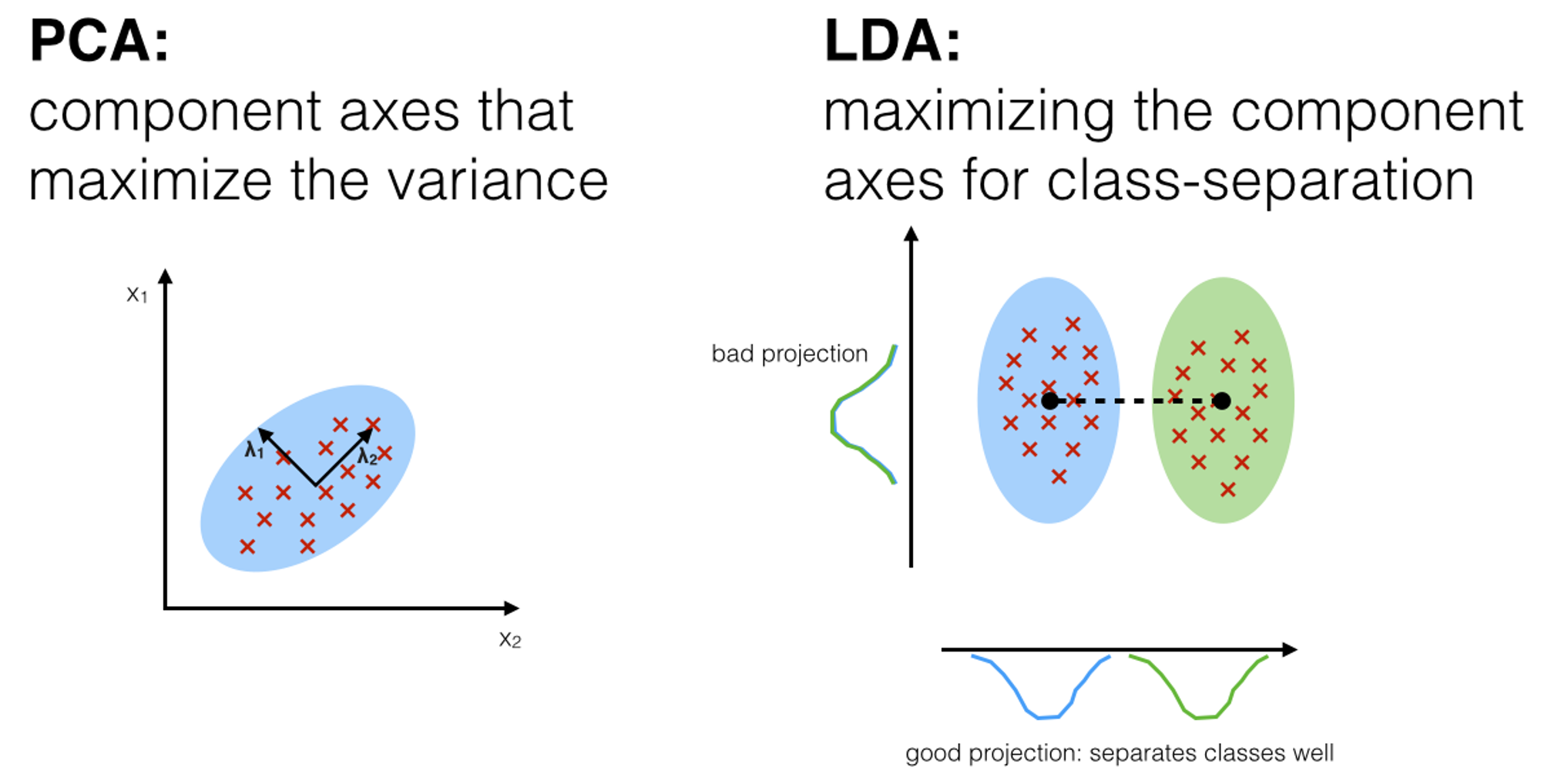
• 따라서 LDA는 공분산 행렬이 아니라 클래스 간 분산과, 클래스 내부 분산 행렬을 생성한 뒤, 이 행렬에 기반해 고유벡터를 구하고 데이터를 투영한다
• 클래스 내부 분산 행렬을 $S_w$, 클래스 간 분산 행렬을 $S_B$라고 하면 다음 식으로 두 행렬을 고유 벡터 분해한다

• 고유값이 가장 큰 순으로 K개 추출하고 그에 해당하는 고유벡터를 이용해 입력 데이터를 변환한다
• PCA는 비지도학습이나, LDA는 클래스가 필요한 지도학습이다

3 SVD(Singular Value Decomposition)

• SVD역시 PCA와 유사하나, PCA의 경우 정방행렬만 고유값 분해 할 수 있으나 SVD는 행과 열이 다른 행렬에도 적용할 수 있다
• SVD는 m x n크기의 행렬 A를 다음과 같이 분해한다

• $U$는 m x m 직교행렬, $\sum$은 m x n 대각행렬, $V^T$는 n x n 직교 행렬
• SVD는 특이값 분해로 불리며, 행렬 U와 V에 속한 벡터는 특이 벡터(sigular vector)이고 모든 특이 벡터는 직교하는 성질이 있다
• $\sum$행렬은 대각행렬이고 대각 성분이 아닌 부분은 모두 0이고 대각성분은 행렬 $A$의 특이값이다