ML-review 회귀(Regression)

• 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법
• 독립변수에 영향을 미치는 값은 회귀계수(Regression coefficients)
• 회귀 계수가 선형이나 아니냐에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다

독립변수 개수	회귀 계수의 결합
1개: 단일 회귀	선형: 선형회귀
여러개: 다중 회귀	비선형: 비선형 회귀

선형 회귀

• 실제 값과 예측 값의 차이를 최소화 하는 직선형 회귀선을 최적화 하는 방식

릿지(Ridge)

• L2규제를 추가한 선형회귀, 큰 회귀 계수 값의 영향도를 감소 시키는(회귀 계수를 작게함) 규제

라쏘(Lasso)

• L1 규제를 적용한 선형회귀, 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 예측 시 피처가 선택되지 않게 한다

엘라스틱넷(ElasicNet)

• L2, L1 규제를 함꼐 결합한 모델

로지스틱 회귀

• 분류에 사용되는 선형모델, 매우 강력한 분류 모델이다

단순 선형 회귀

• 실제 값과 예측 값의 차이 == 잔차를 최소화 하는 직선을 찾는다
• RSS(Residual Sum of Square) 을 목적함수로 한다(오류의 +,- 를 제곱하여 모두 더한다)

• RSS가 최소가 되는 파라미터 w_i를 구할 때는 경사 하강법을 활용해 업데이트한다(람다는 학습률)
  $w_i = w_{i} + \lambda {2 \over N}\sum(실제값_i - 예측값_i)$
• 경사 하강법은 모든 학습 데이터에 대해 반복적으로 업데이트 하기 때문에 수행 시간이 오래걸려 확률적 경사 하강법(SGD)를 많이 활용한다
• SGD는 일부 데이터만을 w를 업데이트 한다

회귀 평가 지표

평가 지표	설명	수식
MAE	오차를 절대값으로 변환해 평균낸다	$MAE = {1\over n}\sum_{i=1}^{n}|Yi - \hat{Yi}
MSE	오차를 제곱 후 평균한다	$MSE = {1\over n}\sum_{i=1}^{n}(Yi - \hat{Yi})^2$
RMSE	MSE는 실제 오류보다 커지므로 루트를 씌운 것이 RMSE	$RMSE = \sqrt{{1\over n}\sum_{i=1}^{n}(Yi - \hat{Yi})^2}$
R^2	분산을 기반으로 성능을 평가한다. 1에 가까울 수록 예측 정확도가 높다	$R^2 = {예측값 Variance \over 실제값 Variance}$

다항(Polynomial) 회귀

• 회귀의 독립변수가 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 회귀

$y = w_0 + w_1*x_1 + w_2*x_2 + w_3*x_1*x_2 + w_4*x_1^2 + w_5*x_2^2$ 과 같이 표현 될 수 있다

• 다항 회귀를 비선형 회귀로 혼동하기 쉽지만 다항 회귀는 선형 회귀이다. 그 이유는 위의 식을 새로운 변수인 Z를

$z = [x_1, x_2, x_1*x_2, x_1^2, x_2^2]$ 으로 한다면 $y = w_0 + w_1*z_1 + w_2*z_2 + w_3*z_3 + w_4 * z_4 + w_5 * z_5$ 와 같이 표현 할 수 있기 때문이다

• 위와 같은 데이터는 단순 선형 회귀 직선 보다 다항 회귀 곡선형으로 더 잘 표현 할 수 있다

편향-분산 Trade off

• 편향-분산 Trade-off 는 머신러닝 모델이 극복해야 할 이슈 중 하나이다
  

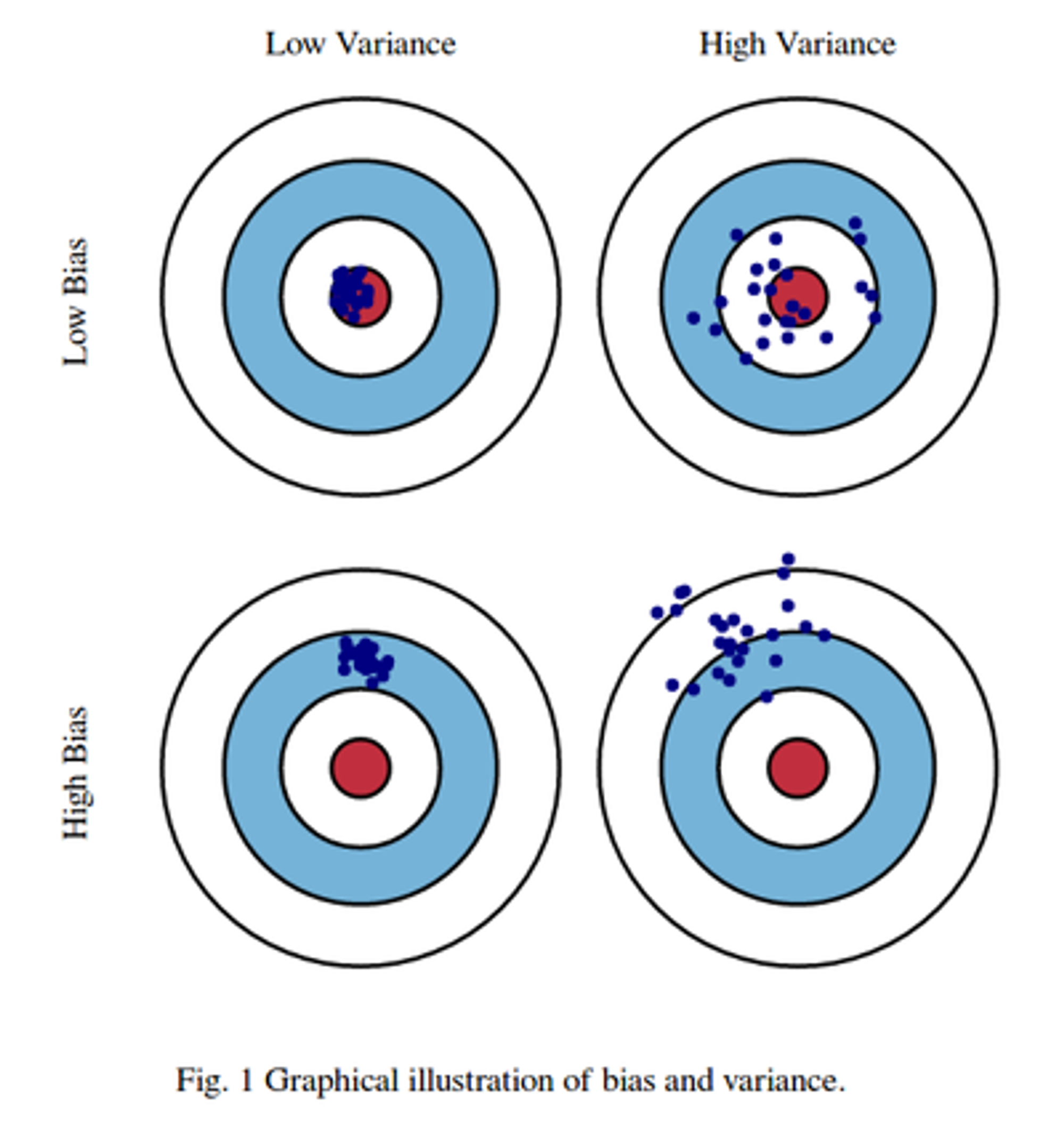
• 일반적으로 편향과 분산은 한쪽이 높으면 한쪽이 낮아지는 경향이 있다
• 편향이 높으면 분산은 낮아지고 → 과소적합
• 편향이 낮으면 분산은 높아진다 → 과적합

규제(Regularization)

• 모델이 과적합되지 않도록 선형회귀 모델의 파라미터에 적절한 규제가 필요하다
• RSS를 최소화 하되, 회귀 계수의 값이 지나치게 커지지 않게 하는 방법이 서로 균형을 이뤄야 한다
• 회귀 계수의 크기를 제어해 과적합을 개선하려면 목적함수가 다음과 같이 변경되어야 한다

• alpha 값은 학습 데이터에 적합 정도와 회귀 계수 값의 크기 제어를 수행하는 파라미터이다
• alpha가 0이면 기존과 동일하게 RSS를 최소화 하는 것이고 alpha를 키워나가면 회귀계수 W를 감소 시킬 수 있다(릿지(L2규제))