우선순위 큐
- 우선순위 큐(priority queue): 우선순위를 가진 항목들을 저장하는 큐
- 우선 순위가 높은 데이터가 먼저 나가게 된다
- 우선 순위 큐는 2가지로 구분한다
- 최소 우선 순위 큐
- 최대 우선 순위 큐
우선순위 큐 구현방법
- 우선순위 큐는 배열, 연결리스트, 힙(heap)을 이용해 구현한다.
보통 시간복잡도를 고려해 경제적인 힙을 사용
배열, 연결리스트, 힙의 삽입과 삭제시 시간복잡도

힙(heap)
-
힙이란 컴퓨터 분야에서 완전이진트리 기반의 "더미"와 모습이 비슷한 특정한 자료 구조를 의미한다.
-
힙은 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
-
힙은 완전이진트리다
-
키값(우선순위)는 중복 가능하다
-
최대 힙(max heap)
- 부모 노드의 키값이 자식 노드의 키 값보다 크거나 같은 완전이진트리
- key(부모노드) >= key(자식노드)
-
최소 힙(min heap)
- 부모 노드의 키값이 자식 노드의 키값보다 작거나 같은 완전이진트리
- key(부모노드) <= key(자식노드)
힙의 구현
- 힙을 저장하는 표준적인 자료구조는 배열이다
- 완전이진트리이므로 각 노드의 인덱스를 붙일 수 있다
- 왼쪽자식 인덱스 = 부모인덱스* 2
- 오른쪽 자식 인덱스 = 부모인덱스* 2+1
- 부모의 인덱스 = 자식의 인덱스/2
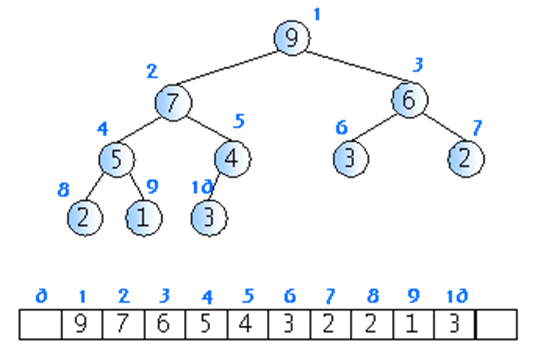
(위 그림은 편의상 1번 인덱스에 루트 노드를 부여)
힙 삽입연산
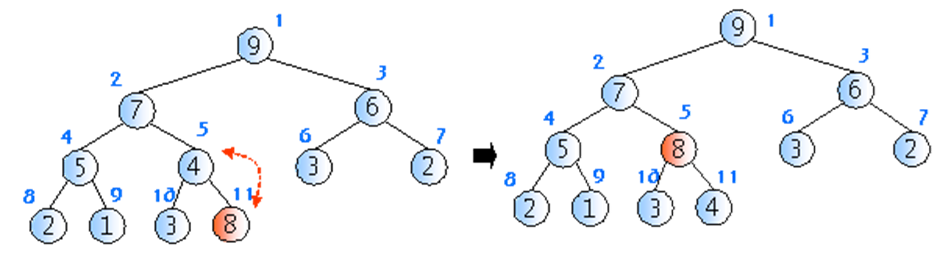
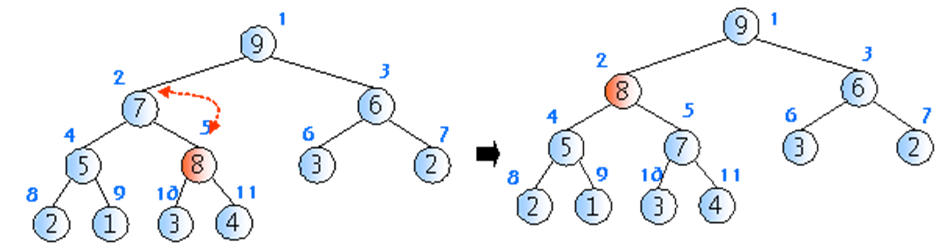
- 힙의 삽입 연산은 회사에서 신입 사원이 들어오면 말단 위치에 앉힌 다음에 위로 올리는것과 비슷하다
- 일단 새로운 노드를 마지막 인덱스에 삽입 후에 부모 노드와 키값을 비교해 교환을 한다
- 힙의 높이가 log n이므로 삽입 연산의 시간 복잡도는 O(log n)이다
#define MAX_ELEMENT 200
typedef struct {
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
// 현재 요소의 개수가 heap_size인 히프 h에 item을 삽입한다.
// 삽입 함수
void insert_max_heap(HeapType *h, element item) {
int i;
i = ++(h->heap_size);
// 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정
while((i != 1) && (item.key > h->heap[i/2].key)) {
h->heap[i] = h->heap[i/2];
i /= 2;
}
h->heap[i] = item; // 새로운 노드를 삽입
}힙 삭제연산
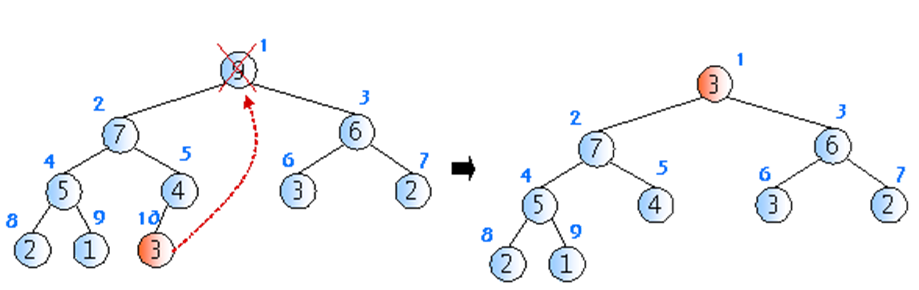
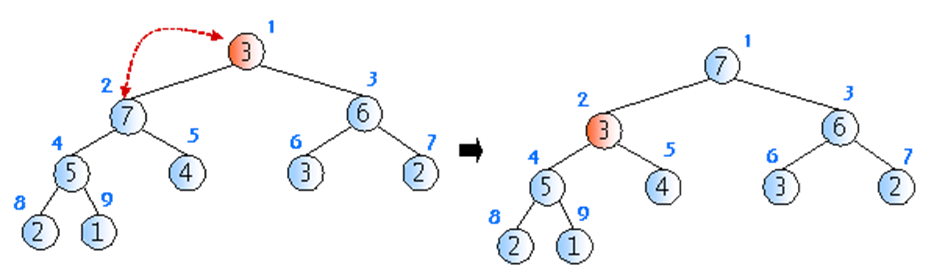
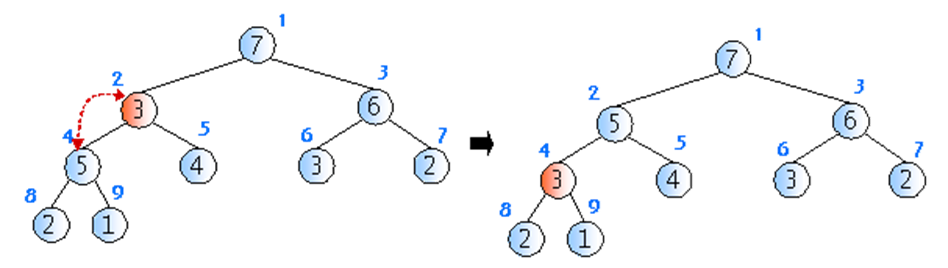
- 삭제연산은 최대값을 갖는 노드를 삭제하는 것이다(최대힙일 경우) 따라서 루트 노드가 삭제된다
- 루트 노드가 삭제 된 후에 힙을 재구성하는 것이 필요하다
- 힙을 재구성할 경우 회사에서 사장의 자리가 비게 되면 먼저 제일 말단 사원을 사장 자리로 올린 다음에, 능력에 따라 강등시키는 것과 비슷하다
- 최악의 경우 트리의 가장 아래 레벨까지 내려가므로 트리의 높이(log n)만큼 시간이 걸린다 시간 복잡도는 O(log n)
element delete_max_heap(HeapType *h) {
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while( child <= h->heap_size ) {
// 현재 노드의 자식노드중 키값이 더 큰 자식노드를 찾는다.
if( ( child < h->heap_size ) &&
(h->heap[child].key) < h->heap[child+1].key)
child++;
if( temp.key >= h->heap[child].key ) break;
// 한단계 아래로 이동
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}힙 정렬
- 힙을 이용하면 정렬 가능하다
-
먼저 정렬해야 할 n개의 요소들을 최대 또는 최소 힙에 삽입한다
-
한번에 하나씩 요소를 힙에서 삭제하여 저장한다
-
하나의 요소를 힙에 삽입하거나 삭제할때 시간이 O(log n) 만큼 소요되고 요소의 개수가 n개 이므로 정렬의 시간복잡도는 O(nlog n)이 걸린다.
void heap_sort(element a[], int n)
{
int i;
HeapType* h;
h = create(); //힙 생성
init(h); //초기화
for (i = 0; i<n; i++) {
insert_max_heap(h, a[i]);
}
for (i = (n - 1); i >= 0; i--) { //비내림차순 정렬
a[i] = delete_max_heap(h);
}
free(h);
}Reference C언어로 쉽게 풀어 쓴 자료구조, 천인국, 공용해, 하상호_2019
상명대학교 홍철의 교수님 강의자료
.jpg)