BCNF & 3NF

Boyce-Codd Normal Form

• 만약 각각의 F+의 FD α → β 에 대해 (α ⊆ R, β ⊆ R) 다음 조건을 최소한 한개 만족한다면 relation schema R을 BCNF라고 한다.

  • α → β is trivial (i.e., β ⊆ α )

  • α가 R의 super key

  • Trivial 하지 않은 모든 함수 종속에서 결정자가 key인 경우 BCNF

• BCNF 가 아닌 스키마

  • instr_dept(ID, name, salary, dept_name, building, budget)

  • dept_name → building, buget 에서 dept_name이 super key가 아니기 때문에 BCNF가 아니다.

Example

• R = (A, B, C)

• F = {A → B, B → C }

• Key = {A}

• R은 BCNF가 아니다.

• 따라서 R을 R1 = (A, B), R2 = (B, C)로 분해하자.

  • R1 과 R2는 BCNF이다

  • Lossless-join decomposition

  • Dependency perserving

Testing for BCNF

• α → β가 BCNF를 위반하는지 확인

  • α+ 를 계산한다.

  • α+가 R의 모든 어트리뷰트를 포함하는지 검증한다. 만약 그렇다면 α+는 R의 super key이다.

• R이 BCNF인지 확인

  • 간소화된 테스트: F+의 모든 dependency를 확인하기 보다는 F내에 BCNF를 위반하는 dependency가 있는지만을 확인한다.

  • BCNF를 test할 때는 F만 고려해도 충분

  • 분해를 할 때는 F+를 모두 고려해야 함!

Testing for BCNF (cont.)

• 그러나, 분해된 relation을 테스트할 때는 F만을 확인하는것은 올바르지 않다.

  ⇒ 반드시 F+를 이용해야한다.
  

• Example

  R (A, B, C, D), F = {A → B, B →C}

  • R1(A, B), R2(A, C, D)로 분해

  • F의 dependency 중 어느 것도 (A, C, D)의 속성만 포함하지 않으므로 R2가 BCNF를 충족한다고 잘못 생각할 수 있다.

  • 하지만 실제로, F+의 dependency A → C는 BCNF가 아니다.

BCNF Decomposition Algorithm

Note: 각 Ri는 BCNF이고 decomposition은 lossless-join이다.

Example of BCNF Decomposition

• 같은 예시를 한 번 더 보자!

• R = (A, B, C)

  F = {A → B, B → C}
  

• Key = {A}

• R is not in BCNF (B가 super key가 아닌데 B → C dependency가 있기 때문)

• Decomposition (이전의 알고리즘을 따라 decompose)

  • R1 = (B, C)
  • R2 = (A, B)

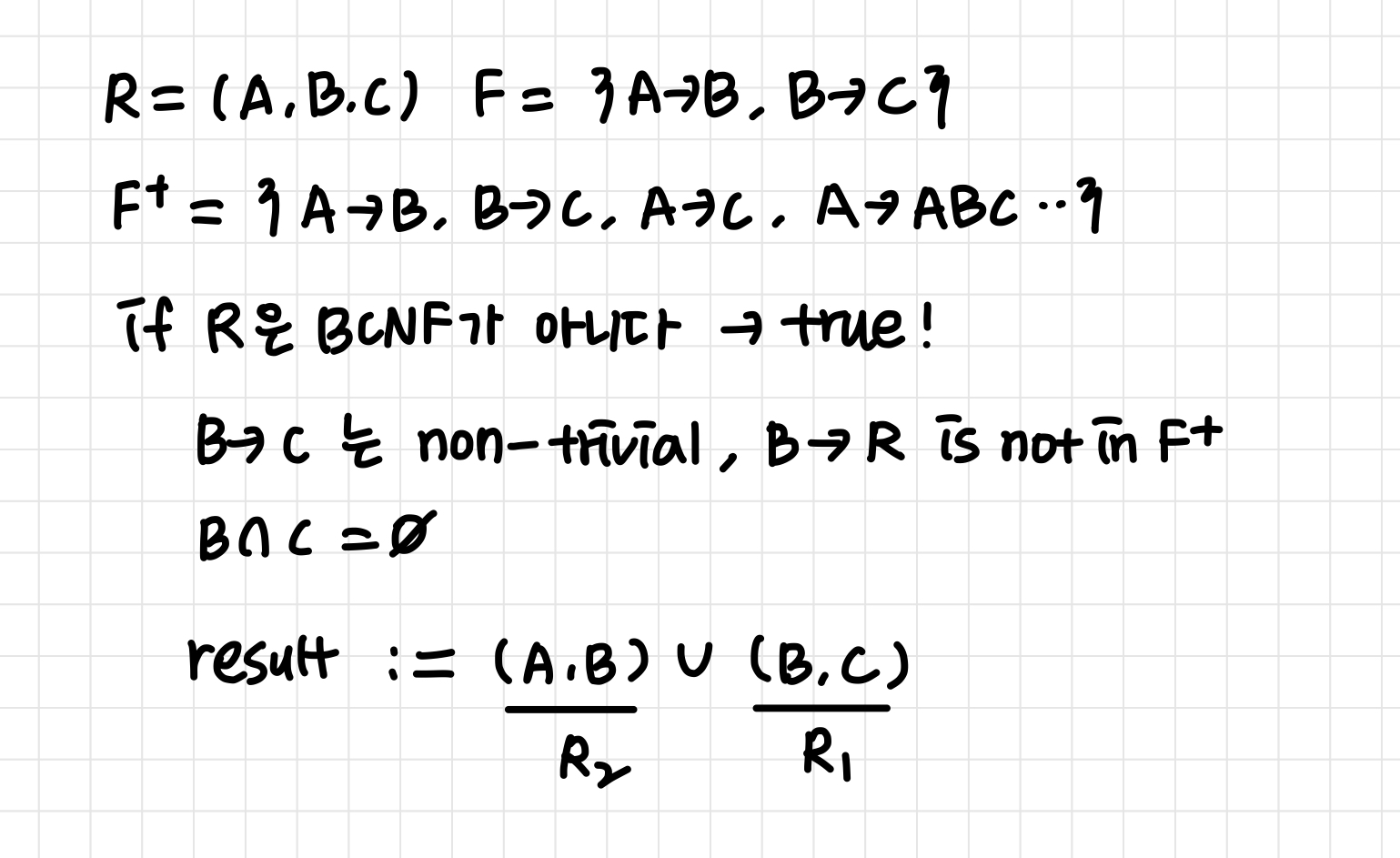
Example of BCNF Decomposition

• class (c_id, title, dept, credits, sec_id, semester, year, building, room, capacity, time_slot_id)

• FD:

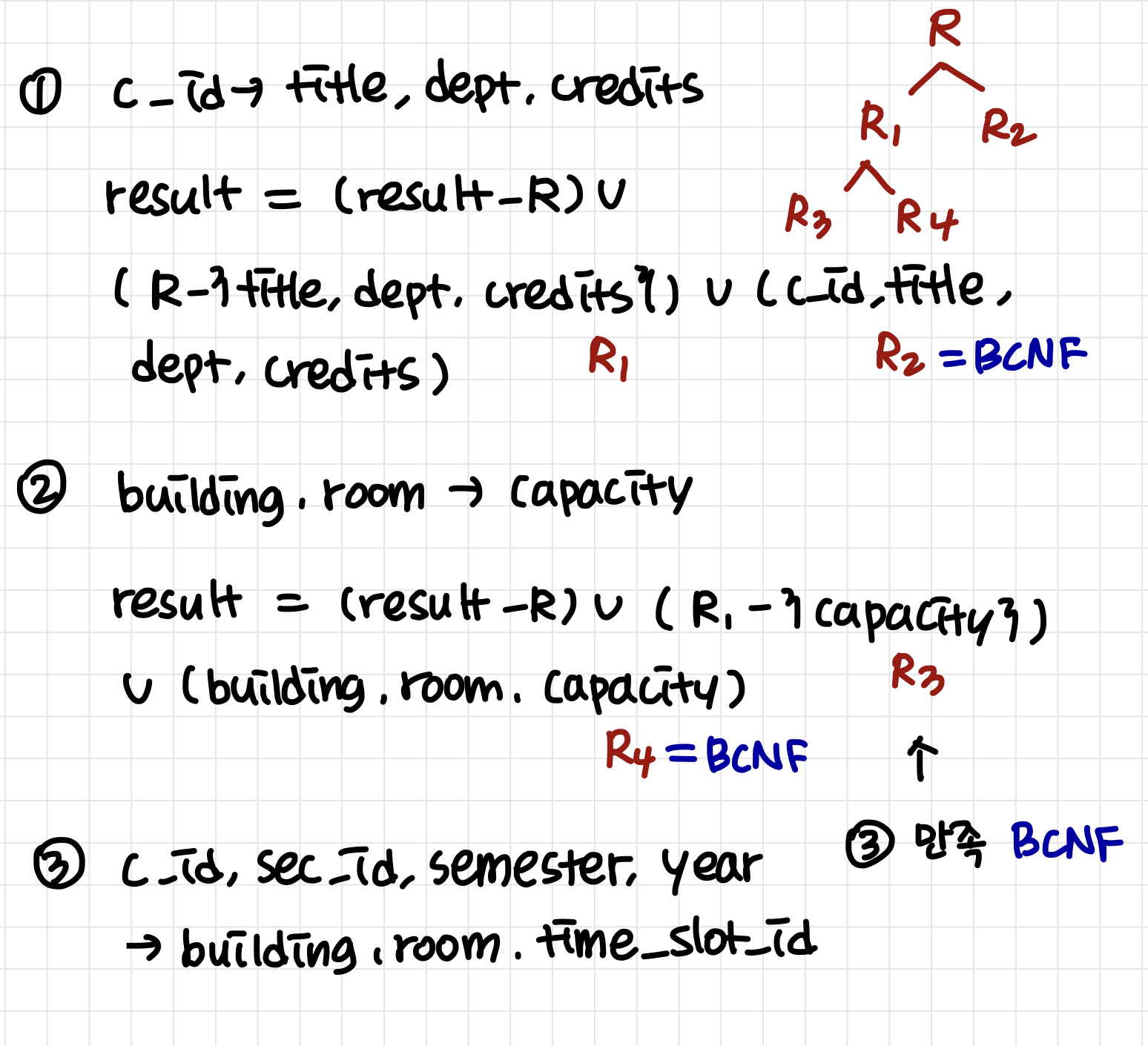
  • c_id → title, dept, credits

  • building, room → capacity

  • c_id, sec_id, semester, year → building, room, time_slot_id

• A candidate key {c_id, sec_id, semester, year}

Example of BCNF Decomposition

• 다시한번 풀어 설명하면 다음과 같다.

• class는 BCNF인가?

  • no: c_id → title, dept, credits

  • Decomposition

    • course (c_id, title, dept, credits) BCNF
    • class-1 (c_id, sec_id, semester, year, building, room, capacity, time_slot_id) NOT BCNF

• course는 BCNF인가?

  • yes (c_id가 superkey임)

• class-1은 BCNF인가?

  • no: building, room → capacity

    • classroom (building, room, capacity) BCNF
    • section (c_id, sec_id, semester, year, building, room, time_slot_id) BCNF

Example

• R = (b-name, b-city, assets, c-name, loan-n, amount)

  F = {b-name → assets, b-city / loan-n → amount, b_name}

  Key = {loan-n, c-name}
  

• Decomposition

  • R1 = (b-name, b-city, assets)

  • R2 = (b-name, c-name, loan-n, amount)

  • R3 = (loan-n, amount, b-name)

  • R4 = (loan-n, c-name)

• Final decomposition result: R1, R3, R4

BCNF and Dependency Preservation

• R = (J, K, L)

  F = {JK → L, L → K}

  2개의 candidate key: JK, JL
  

• R은 BCNF가 아니다. (L → K에서 결정자 L이 super key가 아니기 때문)

• R을 decompose 할 때, 어느 decompose에서는 FD가 not-preserving 한 경우가 발생한다.

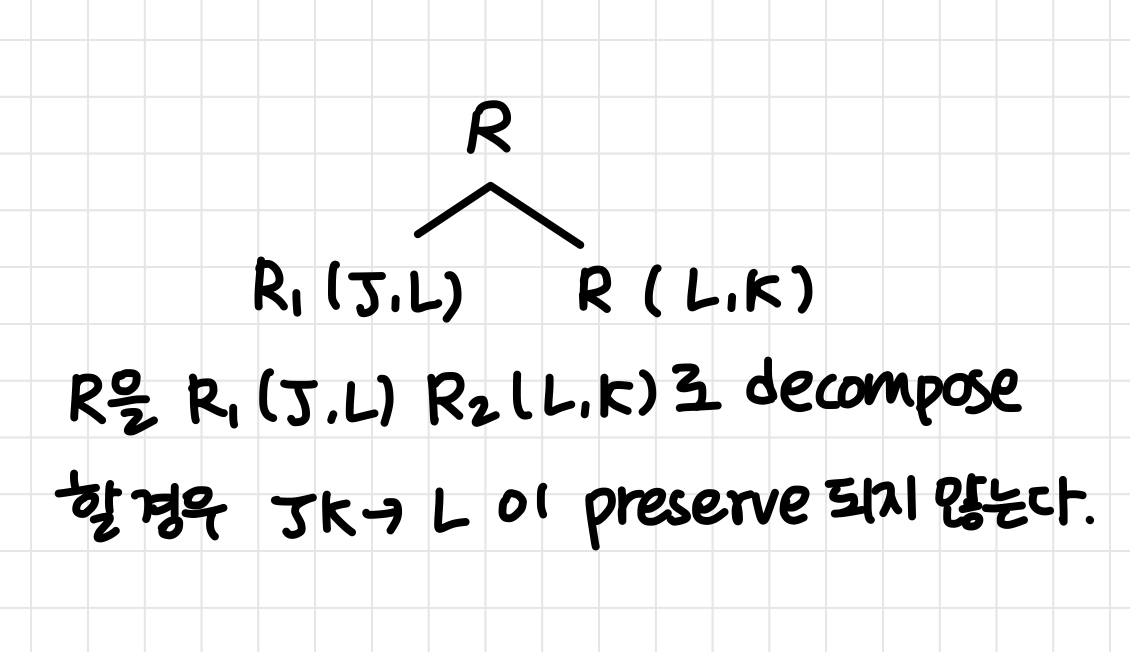
• 이는 JK → L을 확인하기 위해서는 join이 필요함을 암시한다.

이것은 dependency preserving 하는 BCNF decomposition을 얻는 것이 항상 가능한 것은 아니라는 사실을 나타낸다.

• BCNF 분해가 의존성을 보존하지 않을 수도 있음! → BCNF보다 약한 정규형이 필요함 (3NF)

Third Normal Form: Motivation

• 몇 가지 상황이 있다.

  • BCNF가 dependency preserving 하지 않고,

  • 업데이트에서 FD를 위반하는지 효율적으로 확인하는 것이 중요하다.

    (3NF은 업데이트 테스팅을 더 값싼 가격에 할 수 있다.)
    

• Solution: 더 약한 normal form인 Third Normal Form을 정의하는 것이다.

  • 일부 중복을 허용한다. (결과적으로 문제가 발생한다. 후예 예시를 다룰예정)

  • 하지만 FD들은 join 연산 없이 개별 relation으로 체크할 수 있다.

  • 3NF 로의 decomposition은 항상 lossless-join이고, dependency-preserving하다.

Third Normal Form (3NF)

• 만약 F+에 있는 모든 α → β가 다음 조건 중 최소한 한 개 이상 만족하면 relation schema R은 3NF 이다.

  • α → β is trivial (i.e., β ⊆ α )

  • α가 R의 super key이다.

  • β - α 에 있는 모든 어트리뷰트 A는 candidate key를 포함한다.

    (Note: 각 애트리뷰트는 다른 candidate key에 있을 수 있다.)

• BCNF를 만족하지 않는 FD?

  피결정자의 애트리뷰트는 Candidate key의 일부분
  

• BCNF는 항상 3NF에 속함

  (BCNF이면 3NF이다 → True

  3NF이면 BCNF다 → False)
  

3NF Example

• Relation dept_advisor (학과-지도교수)

  • dept_advisor(s_ID, i_ID, dept)

    F = {s_ID, dept → i_ID, i_ID → dept)

    1. 교수는 하나의 전공에만 소속된다.
    2. 학생은 전공별로 한 명의 지도교수를 갖는다.
    3. 학생은 복수 전공이 가능하다.

  • 2개의 candidate key: {s_ID, dept} and {i_ID, s_ID}

  • R은 3NF이다.

    • s_ID, dept → i_ID (s_ID, dept는 super key이다.)

    • i_ID → dept (dept는 candidate key의 일부분에 포함한다.)

  • BCNF는 성립하지 않음 (i_ID → dept)

  • BCNF를 분해할 경우 2.를 검사하는 것이 불가능하다.

3NF Example (cont.)

• R = (J, K, L)

  F = {JK → L, L → K}

  • 2개의 candidate key: JK and JL
  • R은 3NF 이다.
    • JK → L (JK는 super key)
    • L → K (K는 candidate key의 일부분에 포함된다.)

• 이 스키마는 일부 중복이 발생한다.

• BCNF 분해하면 JL, LK로 할 수 있다.

• JK → L을 테스팅하기 위해서는 join이 필요하다.

Redundancy in 3NF

• 이 스키마에는 일부 중복이 발생한다.

• 3NF에서의 중복 때문에 문제가 발생하는 예시이다.

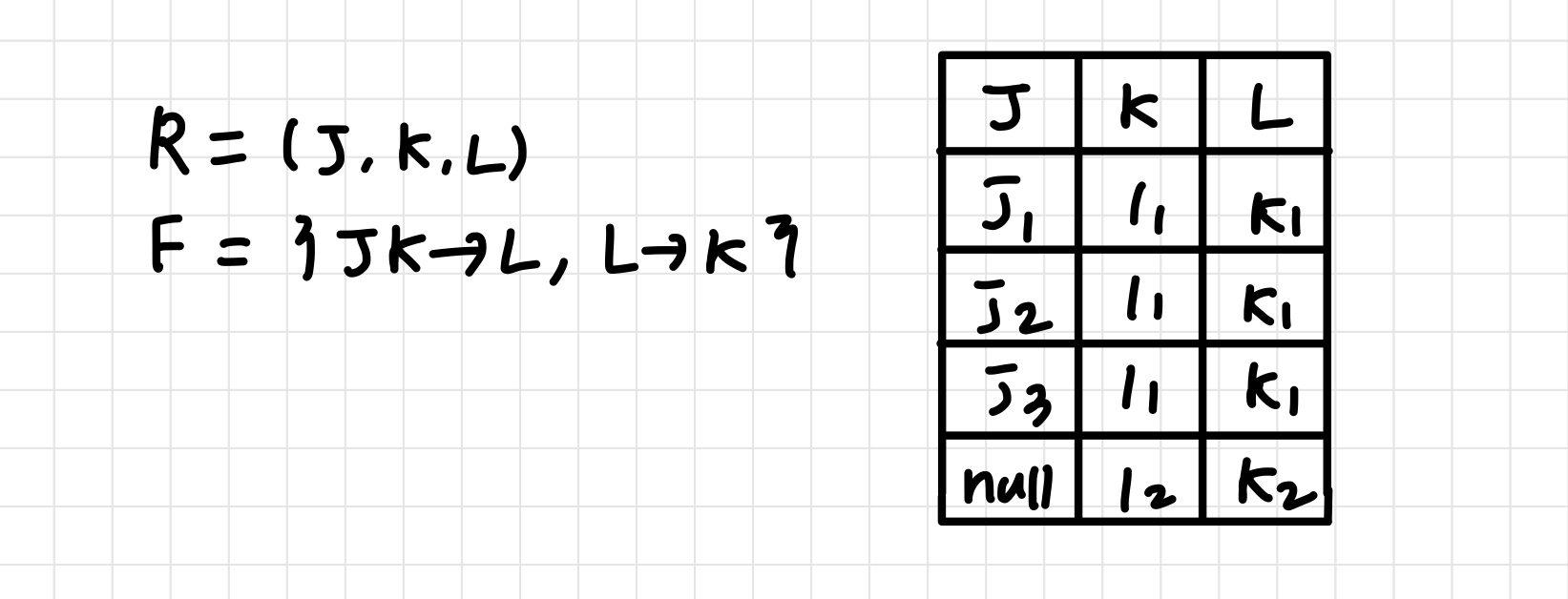
• 정보의 중복 (e.g., the relationship l1, k1)

  • (i_ID, dept_name)

• null 값을 사용이 불가피 (e.g., j와 연관관계가 없는 l2, k2 관계를 표현하기 위해)

  • (i_ID, dept_name)에서 학과에 매칭되어있는 교수가 없는 경우

Testing for 3NF

• F에 있는 FD만을 확인하는 것이 필요하다. (not F+)

• 애트리뷰트 클로저를 사용하여, 각 dependency α → β에 대해 α가 super key인지 확인한다.

• 만약 α가 super key가 아니라면, β에 있는 각 어트리뷰트가 R의 candidate key를 포함하는지 확인해야 한다.

  • 이 테스트 작업은 candidate key를 찾는 것을 포함하므로 비용이 더 비싸다.

  • 3NF 테스팅은 NP-hard 로 보여질 수 있다.

  • 흥미롭게도, 3NF로 분해하는 것은 다항식 시간 내에 수행 가능하다.

3NF Decomposition Algorithm

Example

• Banker = (branch-name, customer-name, banker-name, office-num)

  • Fc: banker-name → branch-name, office-num

    customer-name, branch-name → banker-name

  • The Key: {customer-name, branch-name} , {banker-name, customer-name}

• 3NF?

  • No: banker-name → branch-name, office-num

  • 분해 알고리즘을 따르면 다음과 같다.

    • Banker1 = {banker-name, branch-name, office-num}

    • Banker2 = {customer-name, branch-name, banker-name}

  • Banker2가 candidate key를 포함하므로 이 둘은 3NF를 따른다.

Comparison of BCNF and 3NF

• 3NF

  • Lossless & Dependency Preserving Decomposition 가능

  • Data Redundancy가 존재 → Anomaly 존재할 수 있음

• BCNF

  • Lossless Decomposition 가능

  • Dependency Preserving 불가능할 수 있음

  • Data Redundancy 없음

Comparison of BCNF and 3NF (example)

• R (street, city, zip) street, city → zip zip → city
  

/3NF but not in BCNF (nontrivial & zip is not key)/

• 정보의 중복

• null 값이 블가피함

• R1 (street, zip)

• R2 (city, zip)

/violate 하는 FD의 attr로 하나의 relation 생성/

• 이제 R1과 R2는 BCNF이지만 not dependency-preserving 하다. (street, city → zip dependency가 날아갔기 때문)
  

Normal Forms

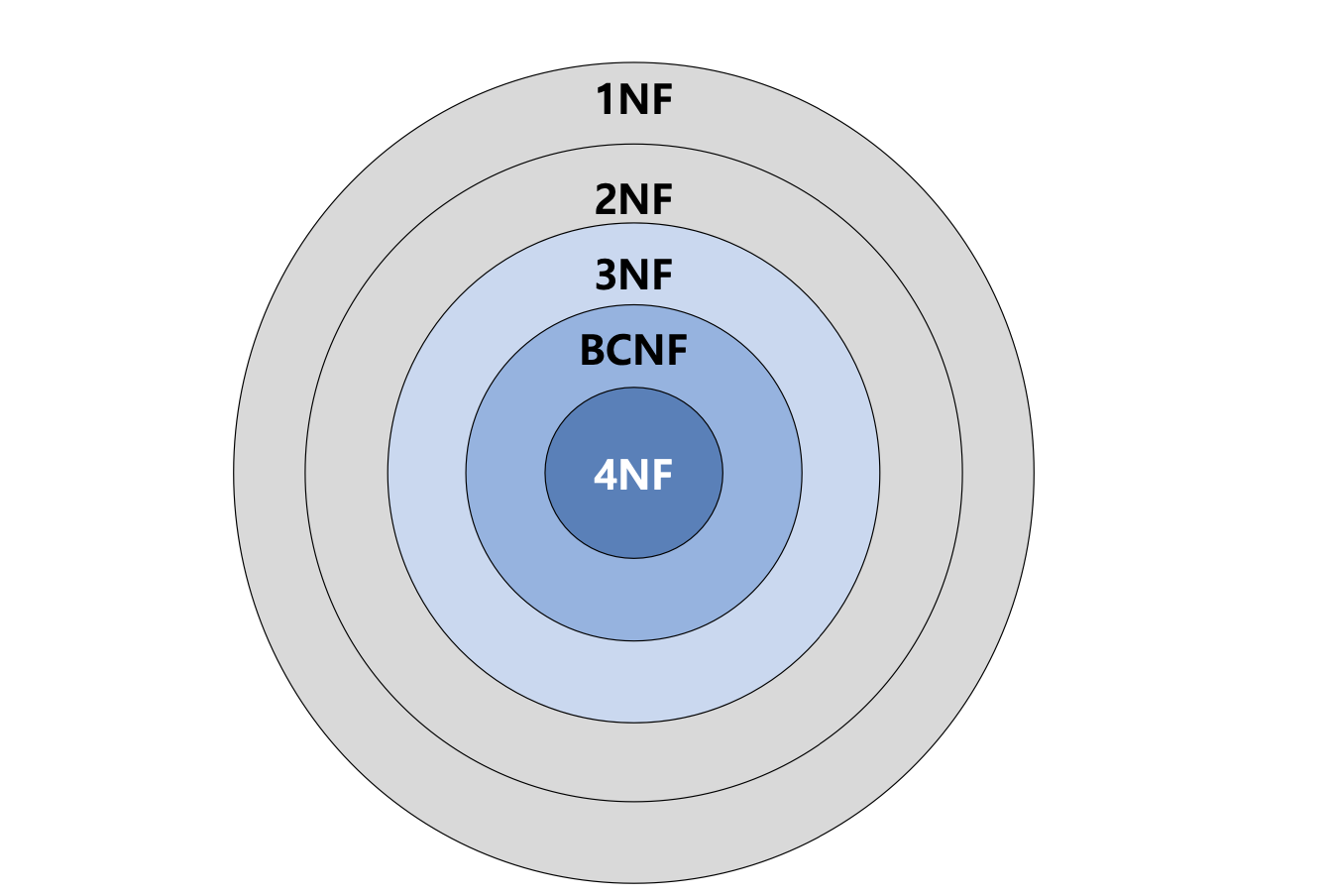
Design Goals

• 릴레이션 데이터베이스의 디자인 목표:

  • BCNF

  • Lossless Join

  • Dependency preservation

• 만약 이를 성취하지 못하면 다음 중 한 가지를 받아들인다.

  • dependency preservation 부족

  • 3NF을 사용함으로서 발생하는 중복

Overall Database Design Process

• 주어진 스키마 R이 있다고 가정한다.

• R은 E-R 다이어그램에서 테이블의 집합으로 변환할 때 생성된다.

• R은 관심있는 모든 어트리뷰트를 포함하는 단일 릴레이션이 될 수 있다. (called universal relation)

• 정규화는 R을 더 작은 릴레이션으로 분해한다.

• R은 우리가 정규화된 형태로 테스트/변형할 수 있는 릴레이션의 특별한 디자인에 의한 결과가 될 수 있다.

ER Model and Normalization

• E-R 다이어그램이 주의깊게 설계되고 모든 엔티티가 정확하게 식별될 때, E-R 다이어그램에 의해 생성된 테이블은 더 이상 정규화가 필요하지 않다.

• 그러나, 실제 (불완전한) 설계는 엔티티의 키가 아닌 애트리뷰트에서 엔티티의 다른 애트리뷰트로의 FD가 있을 수 있다.

  • e.g. employ entity with attribute (department-number, department-address) 이에 대한 FD {department-number → department-address}

  • 좋은 설계는 department 엔티티를 따로 만드는 것이다.

• 관계 집합(두 개 이상의 엔터티 집합 포함)의 키가 아닌 애트리뷰트의 FD가 드물지만 가능하다 --- 대부분의 관계는 이진이다.

Denormalization for Performance

• 성능을 위해 비정규화된 스키마를 사용하길 원할 수 있다.

• e.g. customer-name을 account-number, balance와 함께 보여주기 위해서는 account와 depositor을 join해야 한다.

• 대안책 1: account 뿐만아니라 depositor의 어트리뷰트를 포함하는 비정규화된 relation을 사용한다.

  • 더 빠른 조회

  • 업데이트를 위한 추가 공간 및 추가 실행 시간

  • 프로그래머를 위한 추가 코딩 작업 및 추가 코드의 오류 가능성

• 대안책 2: account ⋈ depositor 으로 정의된 구체화된 뷰를 사용한다. (이미 있는 account 테이블, depositor 테이블 냅두고 새롭게 또 정의)

  • 단점과 장점은 위와 동일하다.

  • 프로그래머가 해야할 추가 코딩 작업 없음 (done by DBMS)

  • 발생가능한 에러 피함.

보완해야할 부분이 있으면 댓글로 알려주세요 :)