Normal Form

삼식이·2023년 4월 15일

Database

데이터베이스

목록 보기

5/12

Normal Form

정규화의 기본 목표는 테이블 간에 중복된 데이터를 허용하지 않는다는 것이다. 중복된 데이터를 허용하지 않음으로써 무결성(integrity)를 유지할 수 있으며, DB의 저장 용량 역시 줄일 수 있다.
이러한 테이블을 분해하는 정규화 단계가 정의되어 있는데, 테이블을 어떻게 분해하는지에 따라 정규화 단계가 달라진다.
정규형은 제 1 정규형, 제 2정규형, 제 3 정규형, BCNF, 제 4 정규형, 제 5 정규형이 있다.
- 제 4 정규형과 제 5 정규형은 실무적으로 잘 쓰이지 않는다. 따라서 다루지 않을 예정이다.

1NF (제 1 정규형)

앞서 살펴보았던 1NF에 대해 다시 한번 정리하겠다.

예시 1

1NF 는 릴레이션 컬럼의 도메인 값이 모두 원자값 (atomic value) 만을 갖도록 테이블을 분해하는 것이다.(원자값이란 더 이상 쪼개질 수 없는 단위를 말한다.)

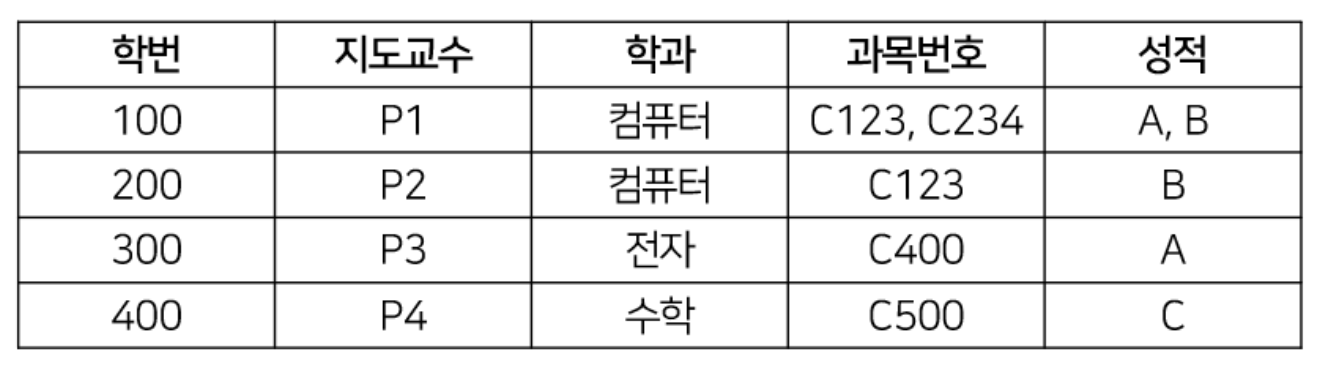
위의 릴레이션의 경우 1NF를 만족하지 못한다. 학번이 100인 학생의 과목 번호와 성적이 2개로 이루어져 있기 때문이다. (non-atomic, divisible) 따라서 1NF이 되려면 다음과 같이 속성 값을 분리해주어야 한다.

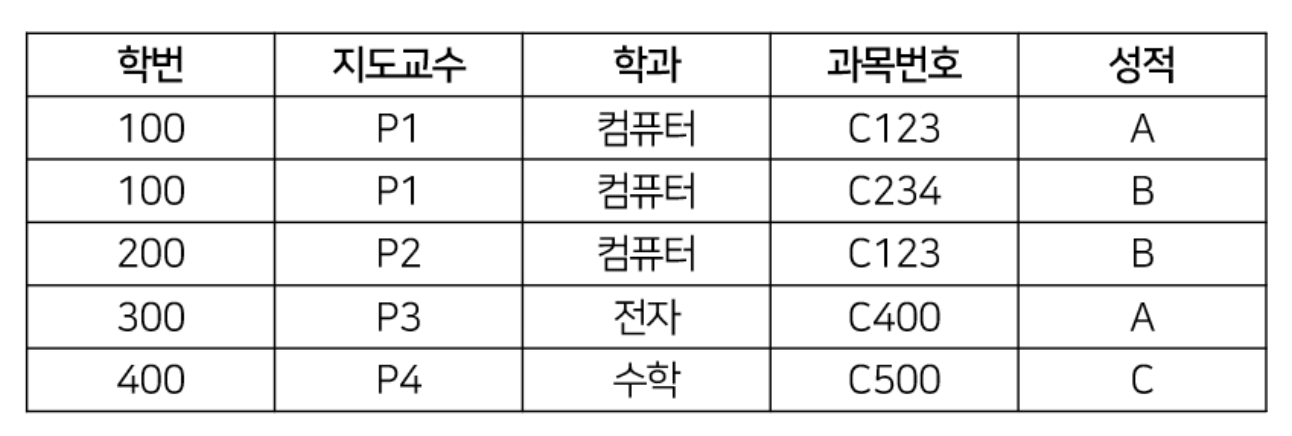
1NF에서 발생하는 anomaly(이상현상)
- 삽입 이상: 학생이 새 과목을 수강신청할 때 반드시 학생의 학과와 지도교수를 알아야한다. (불필요한 정보)
- 삭제 이상: 300번 학생이 C400 과목을 취소하면, 해당 과목에 대한 정보가 모두 사라진다.
- 갱신 이상: 100번 학생이 지도교수를 변경할 때. P1인 행을 모두 찾아서 변경해주어야 한다. (이때 정보의 inconsistency가 발생할 수 있음)
1NF에서 anomaly가 발생하는 이유는, 기본키(primary key)가 아닌 속성들이 기본키에 완전 함수 종속되지 못하고 부분 함수 종속되어 있기 때문이다. 즉, 기본키의 일부 속성에만 의존하고 있기 때문이다.
아래 그림을 참고하면 기본키는 (학번, 과목 번호) 이고, 지도 교수와 학과가 부분 함수 종속되어 있다.

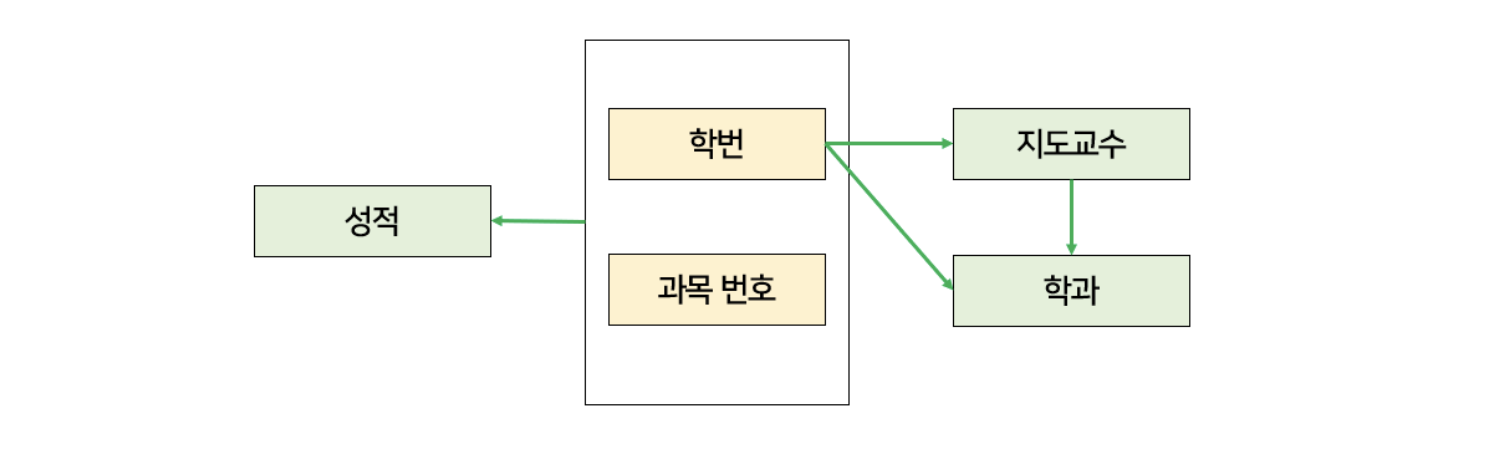
예시 2

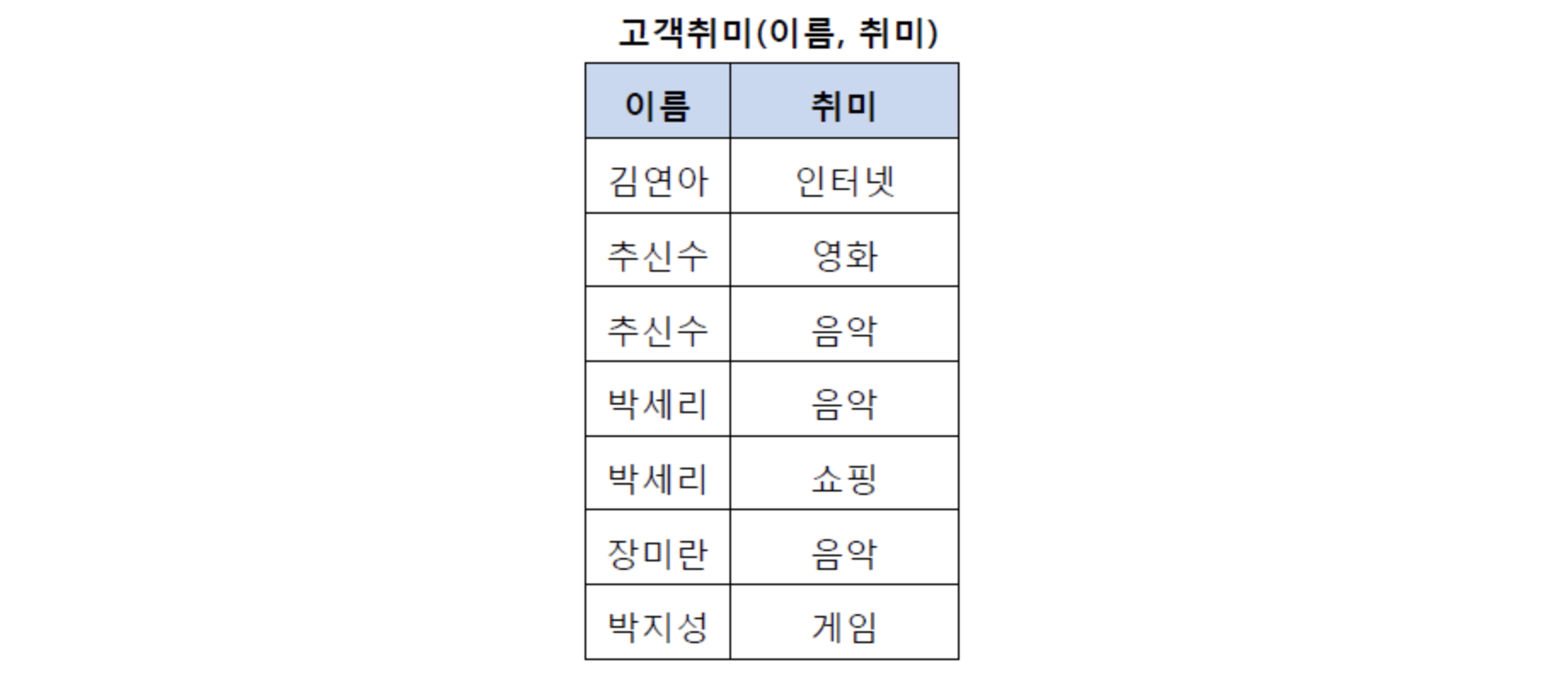
아래와 같은 고객 취미 테이블이 존재한다고 하자.

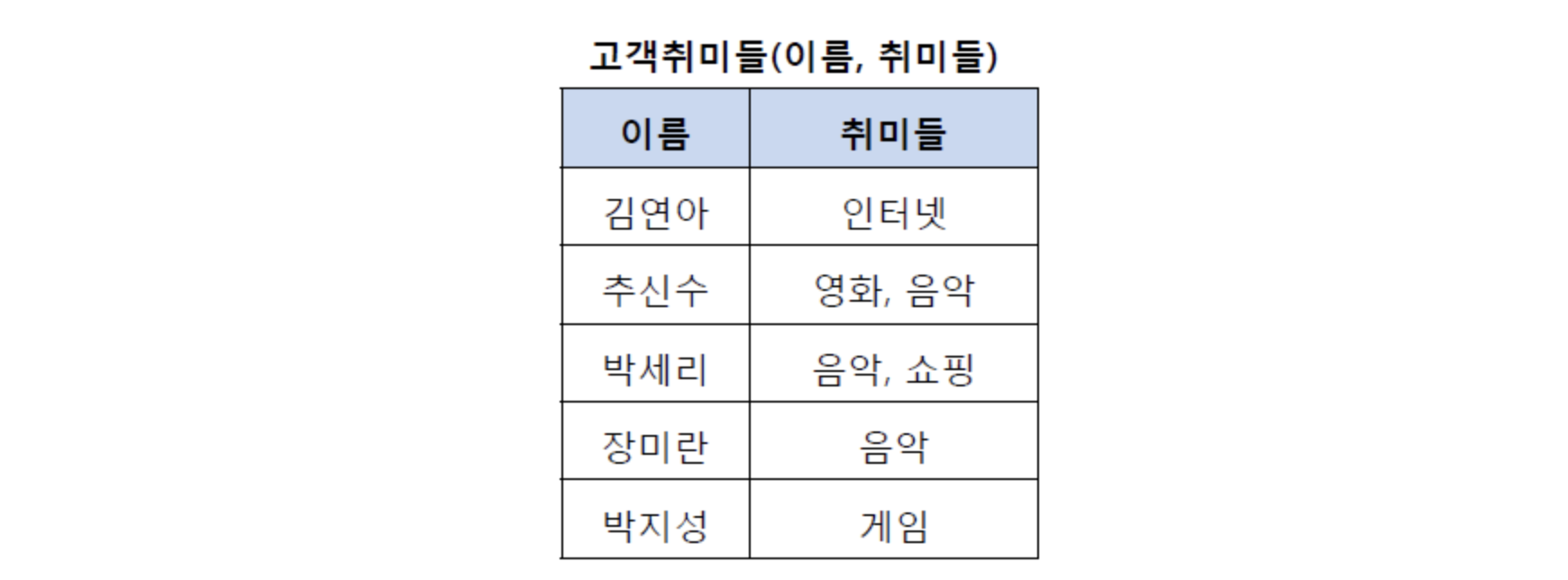
위의 테이블에서 추신수와 박세리는 여러 개의 취미를 가지고 있기 때문에 1NF를 만족하지 못한다. 따라서 이를 1NF로 정규화하여 분해할 수 있다.
1NF 를 진행한 테이블은 다음과 같다.

2NF (제 2 정규형)

예시 1

2NF는 1NF 이면서, 기본키(primary key)에 속하지 않은 속성 모두가 기본키에 완전 함수 종속 하도록 테이블을 분해하는 것이다.
- 여기서 완전 함수 종속이란 기본키의 부분집합이 결정자가 되어선 안된다는 것을 의미한다.

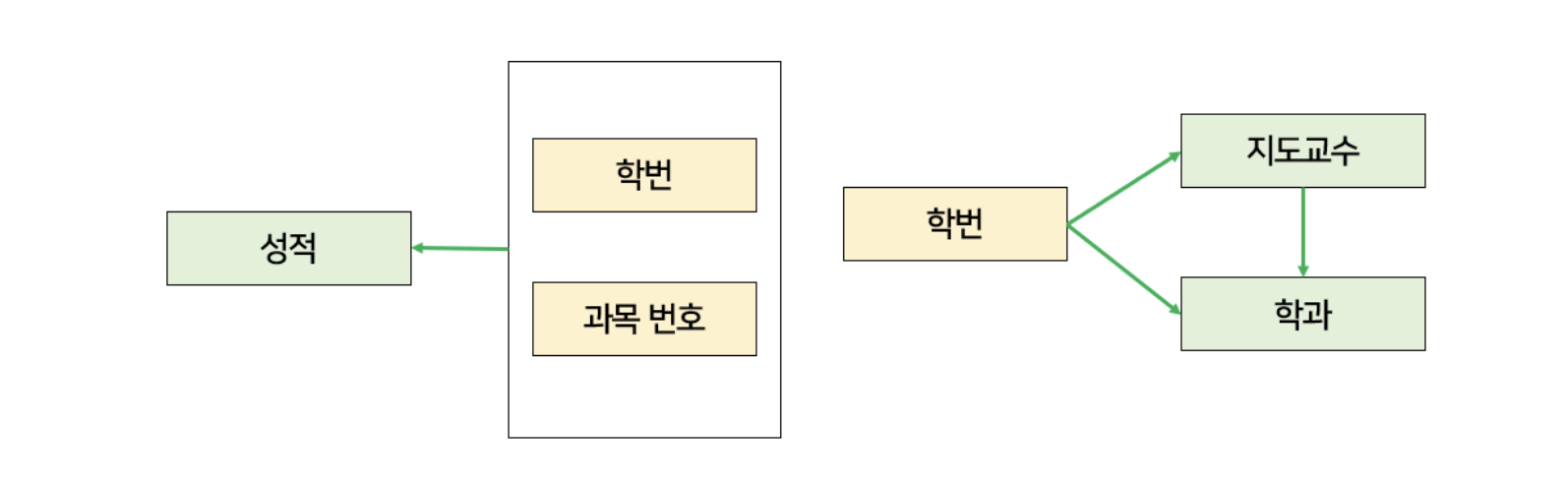
위 그림처럼 각 속성들이 모두 완전 함수 종속이 되도록 릴레이션을 분리시켜준다. 따라서 아래와 같이 릴레이션이 형성된다.

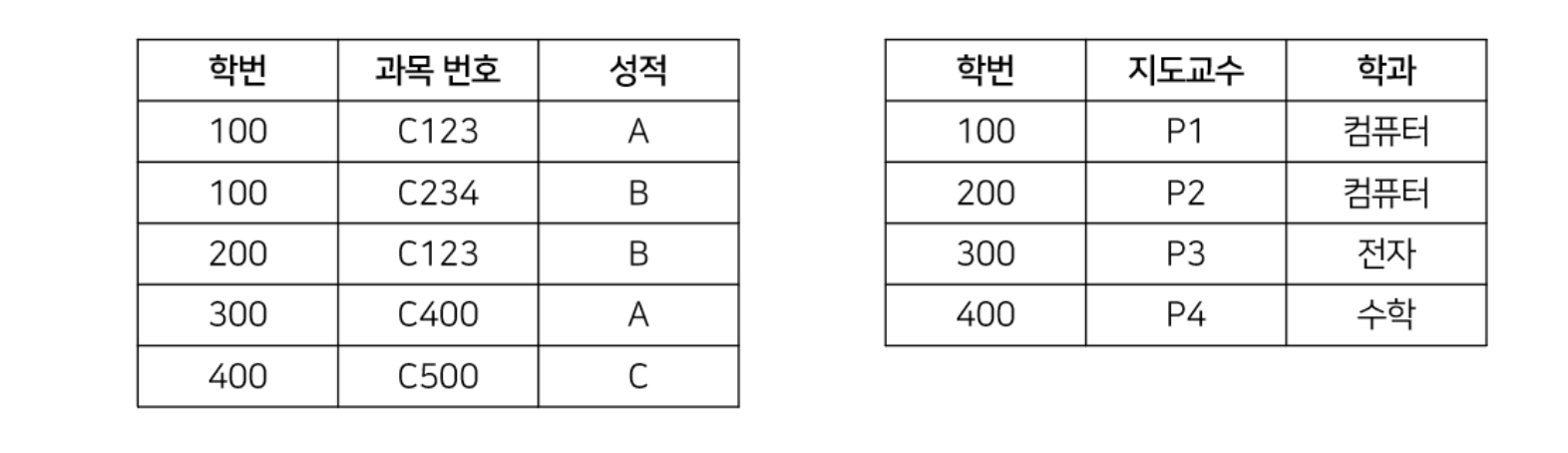
2NF 에서 발생하는 anomaly(이상현상)
- 삽입 이상: 지도 교수가 학과에 소속되어 있음을 추가살때 반드시 지도 학생이 있어야 한다. (불필요한 정보 필요)
- 삭제 이상: 300번 학생이 자퇴하는 경우 P3 교수의 학과 정보가 사라진다.
- 갱신 이상: 지도 교수의 학과가 변경되는 경우 모두 찾아서 변경시켜주어야 한다. (지도 교수가 동일한 학생이 여러 명 있는 경우)
2NF에서 anomaly가 여전히 발생하는 이유는 이행적 함수 종속성 때문이다. 이행적 함수 종속성은 속성 A → B 이고, B → C 이면서 A → C의 관계에 있는 것을 말한다.
위 예시에서는 학번 → 지도교수, 지도교수 → 학과, 학번 → 학과의 관계가 존재한다.
따라서 지도교수의 학과를 추가하기 위해서 지도 학생까지 필요하게 되고, 학생이 자퇴할 경우 지도 교수의 학과 정보까지 사라지게 되는 문제가 발생하게 되는 것이다.

예시 2

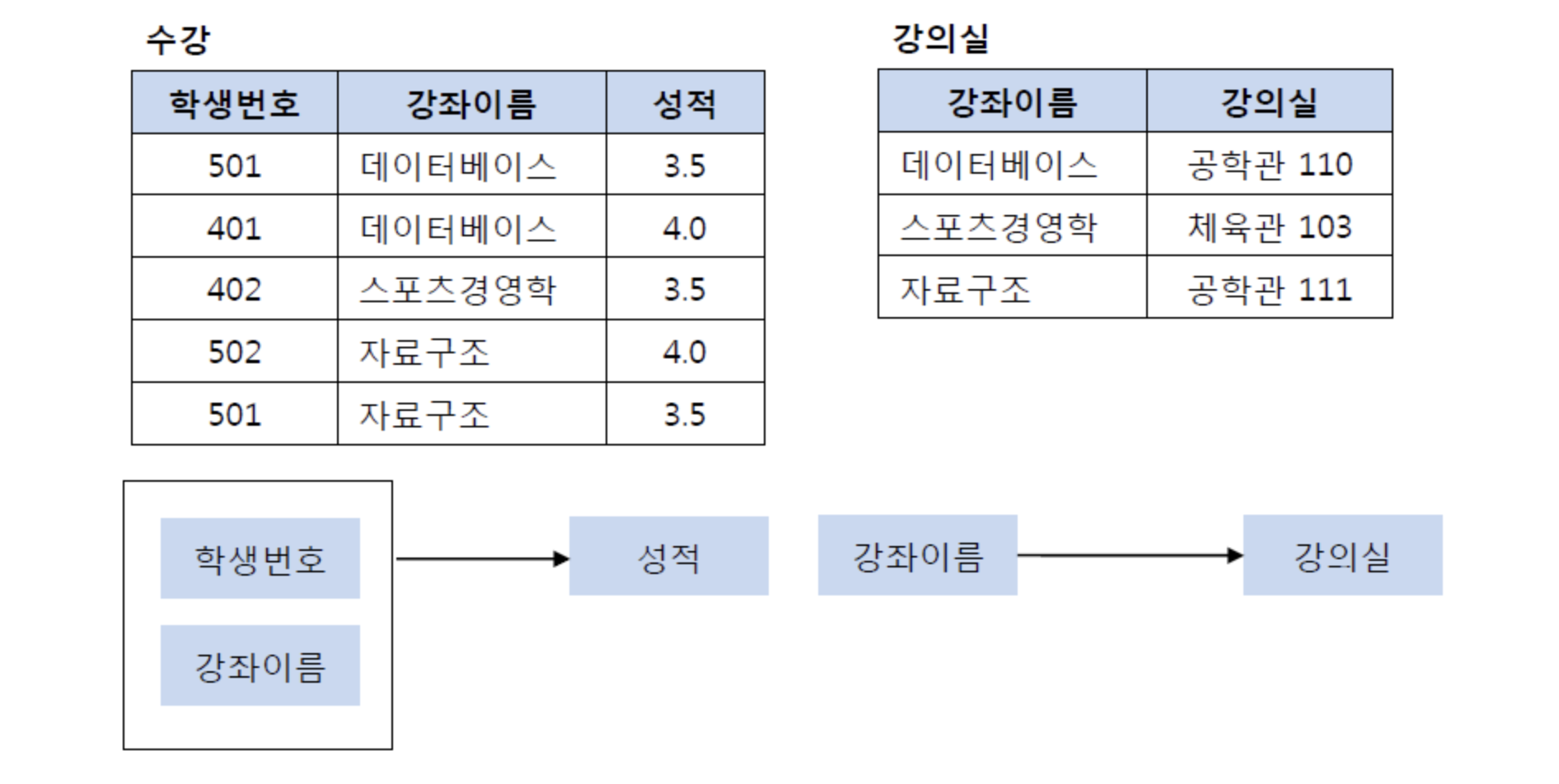
아래와 같은 수강 강좌 테이블을 살펴보자.

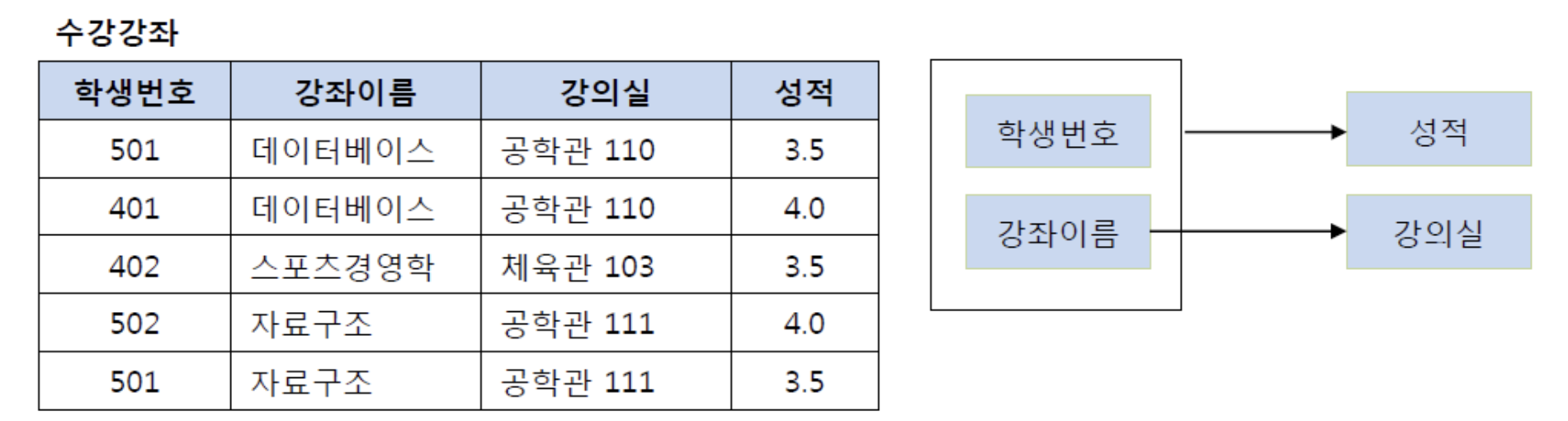
이 테이블에서 기본키는 (학생번호, 강좌이름)으로 복합키이다. 그리고 (학생번호, 강좌이름)인 기본키는 성적을 결정하고 있다.
- (학생번호, 강좌이름) → (성적)
그런데 여기서 강의실이라는 컬럼은 기본키의 부분집합인 강좌이름에 의해 결정될 수 있다.
- (강좌이름) → 강의실
즉, 기본키 (학생번호, 강좌이름)의 부분키인 강좌이름이 결정자이기 때문에 위의 테이블의 경우 다음과 같이 기존의 테이블에서 강의실을 분리하여 2NF를 만족시킬 수 있다.

3NF (제 3 정규형)

예시 1

3NF는 2NF 이면서, 이행적 함수 종속성을 제거해 테이블을 분해하는 것을 말한다.
즉, 기본키에 속하지 않은 모든 속성이 기본 키에 이행적 함수 종속이 아닐 때 3NF 라고 한다.
다르게 표현하면, 기본키 이외의 속성이 그 외 다른 속성을 결정할 수 없는 것이다.

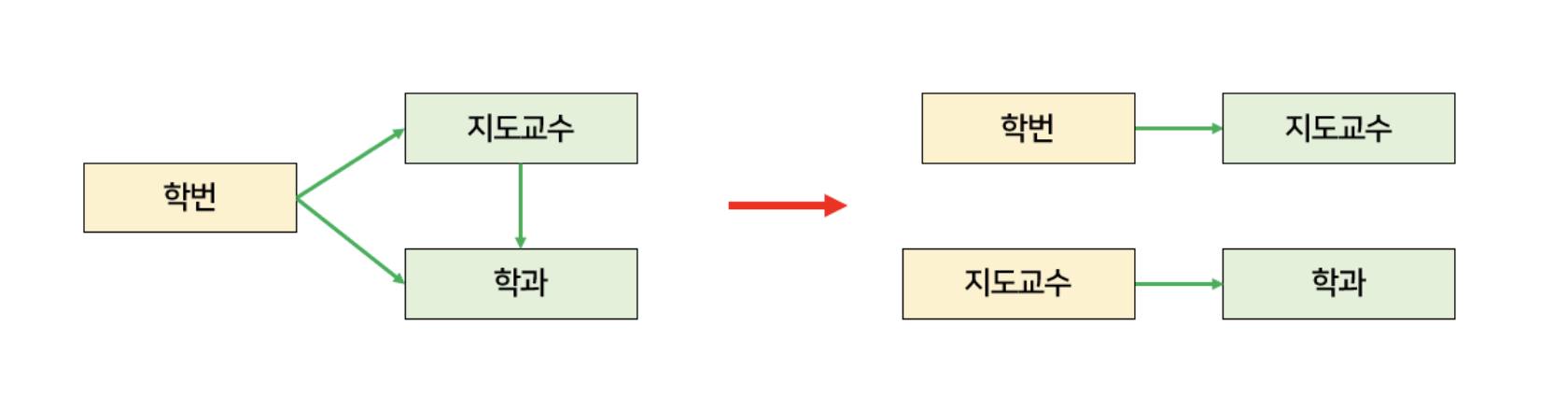
이렇게 이행적 함수 종속 관계에 있는 속성을 분리한다. 테이블로 나타내면 아래와 같다.

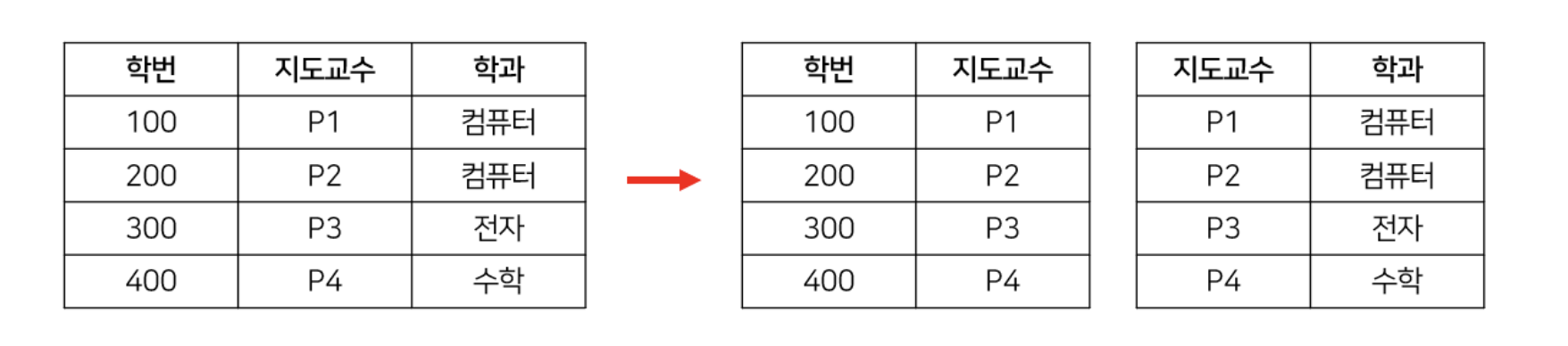
예시 2

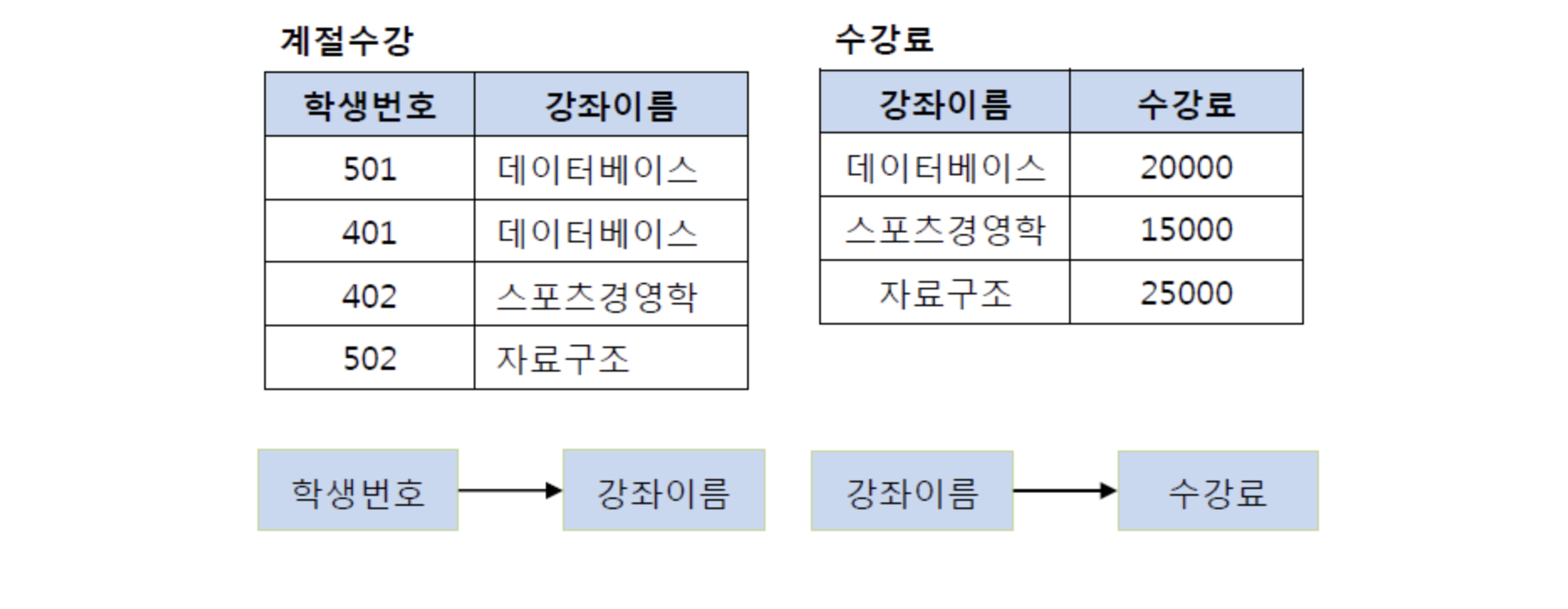
아래와 같은 계절 학기 테이블을 살펴보자.

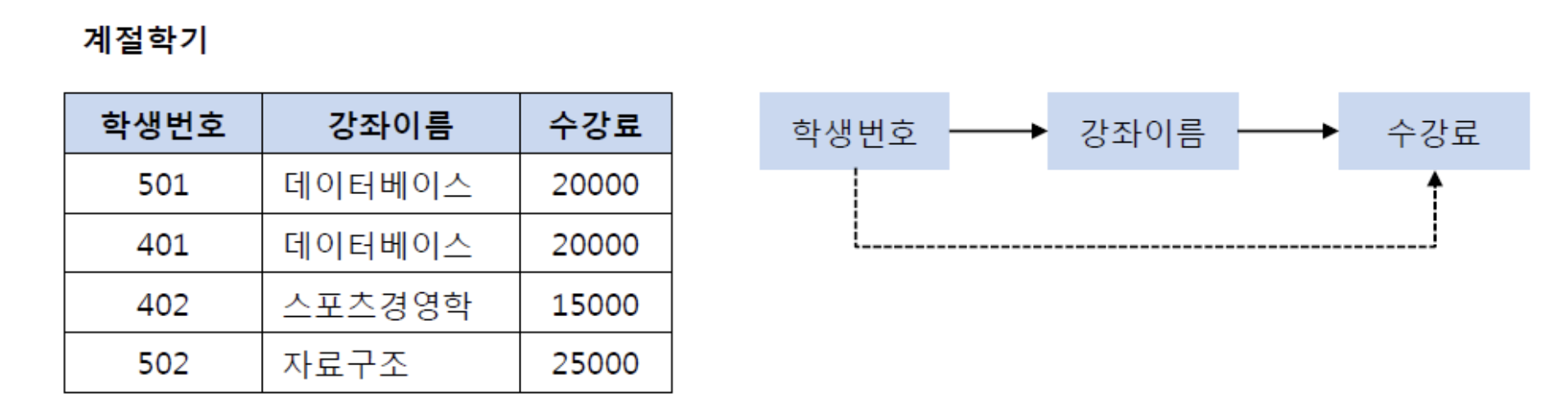
기존의 테이블에서 학생 번호는 강좌 이름을 결정하고 있고, 강좌 이름은 수강료를 결정하고 있다.
- 이행적 함수 종속성: (학생번호) → (강좌이름), (강좌이름) → (수강료), (학생번호) → (수강료)
그렇기 때문에 이를 (학생번호, 강좌이름) 테이블과 (강좌이름, 수강료) 테이블로 분해해야한다.
이행적 함수 종속성을 제거하는 이유는 비교적 간단하다.
예를 들어, 501번 학생이 수강하는 강좌가 스포츠경영학으로 변경되었다고 하자. 이행적 함수 종속성이 존재한다면 501번의 학생은 스포츠경영학이라는 수업을 20000원이라는 수강료로 듣게 된다. 물론 강좌 이름에 맞게 수강료를 다시 변경할 수 있지만, 이러한 번거로움을 해결하기 위해 3NF를 하는 것이다.
- 또한 이때 강좌 이름이 변경되고 수강료를 변경하지 않을 경우 갱신 anomaly가 발생할 수 있다.
즉, 학생 번호를 통해 강좌 이름을 참조하고, 강좌 이름으로 수강료를 참조하도록 테이블을 분해해야 하며 그 결과는 다음의 그림과 같다.

Boyce-Codd Normal Form

예시 1

BCNF는 3NF를 조금 더 강화시킨 개념이다. 강한 3NF이라고도 부른다.
BCNF란 3NF를 진행한 테이블에 대해 모든 결정자가 후보키가 되도록 테이블을 분해하는 것이다.
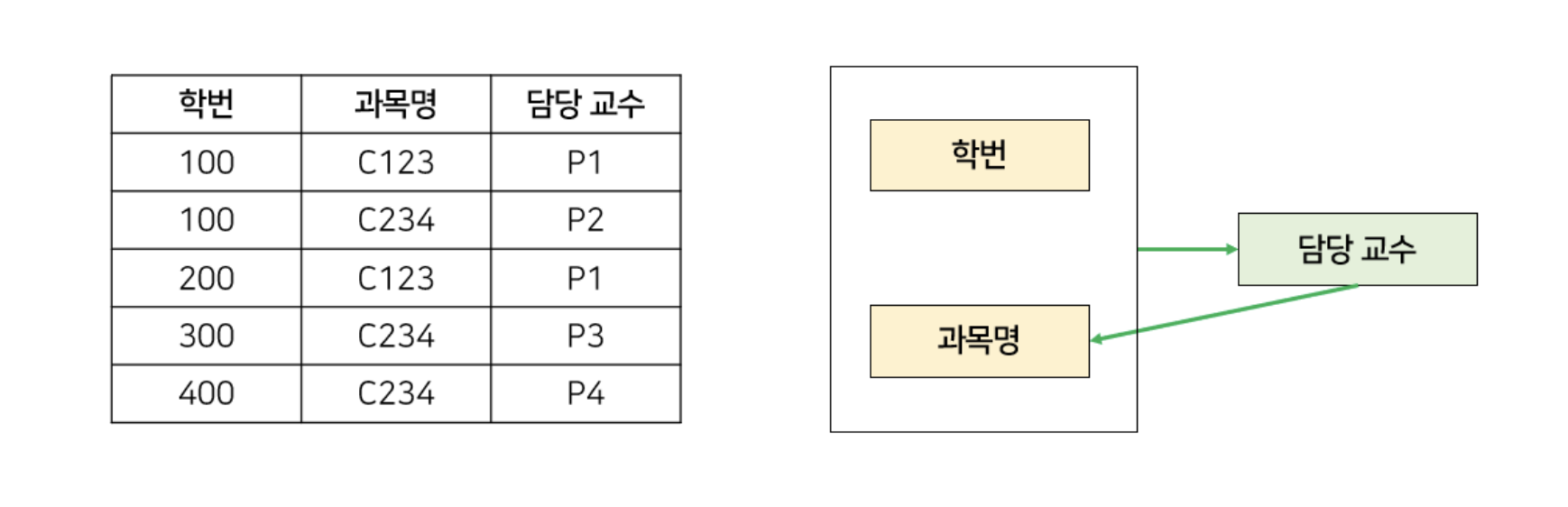
아래와 같은 3NF를 만족하는 릴레이션이 있다고 가정하자. 한 교수당 하나의 수업만 맡는다고 가정한다.

이렇게 되면 3NF를 만족한다. 이 경우 어떤 anomaly가 발생할까?
- 삽입 이상: 새로운 교수가 특정 과목을 담당한다는 새로운 정보를 추가할 수 없다. 적어도 한 명 이상의 수강학생이 필요하다.
- 삭제 이상: 학번 100이 C234 과목을 취소하면, P2가 C234 과목을 담당한다는 정보도 삭제된다.
- 갱신 이상: P1의 과목이 변경되면 P1인 행을 모두 찾아 변경시켜주어야 한다.
이런 anomaly가 생기는 이유는, 결정자가 후보키로 취급되고 있지 않기 때문이다.
후보키는 슈커피 중에서 최소성을 갖는 키이므로 이 릴레이션에서는 (학번, 과목명)이나 (학번, 담당교수)가 후보키가 된다. 담당 교수만으로는 후보키가 될 수 없다.
하지만, 후보키가 아님에도 과목명을 결정할 수 있기 때문에 담당 교수는 결정자에 속한다.
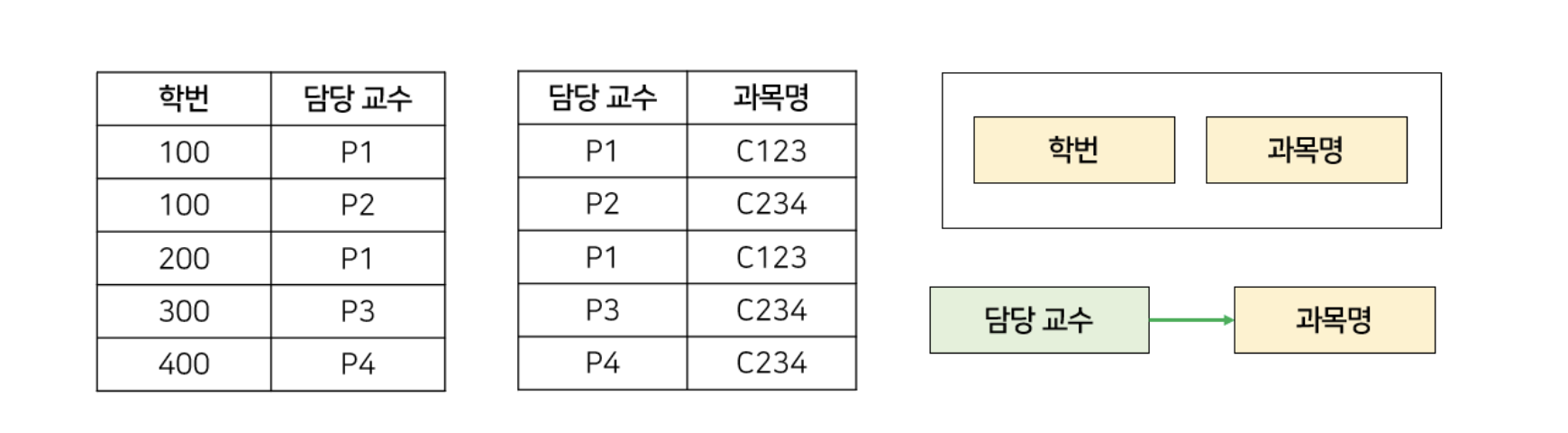
이 anomaly를 해결하기 위해서 모든 결정자는 항상 후보키가 되도록 릴레이션을 decompose 해주면 강한 3NF, 즉 BCNF를 만족하게 된다.

예시 2

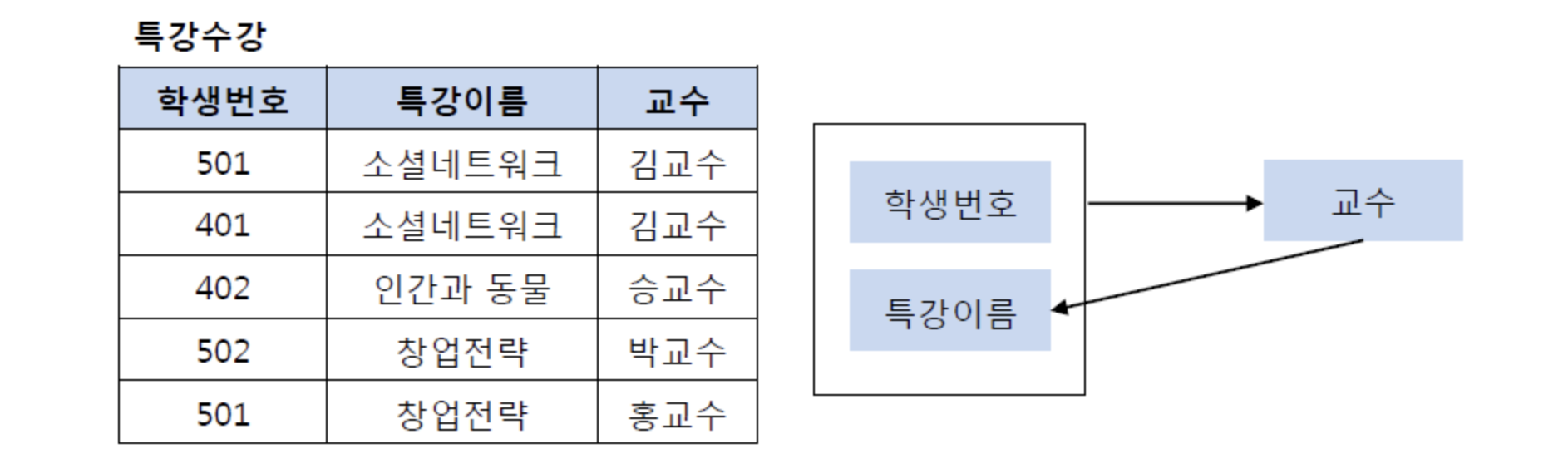
다음과 같은 특강수강 테이블이 존재한다고 하자.

특강수강 테이블에서 기본키는 (학생번호, 특강이름)이다. 그리고 기본키 (학생번호, 특강이름)는 교수를 결정하고 있다. 또한 여기서 교수는 특강이름을 결정하고 있다.
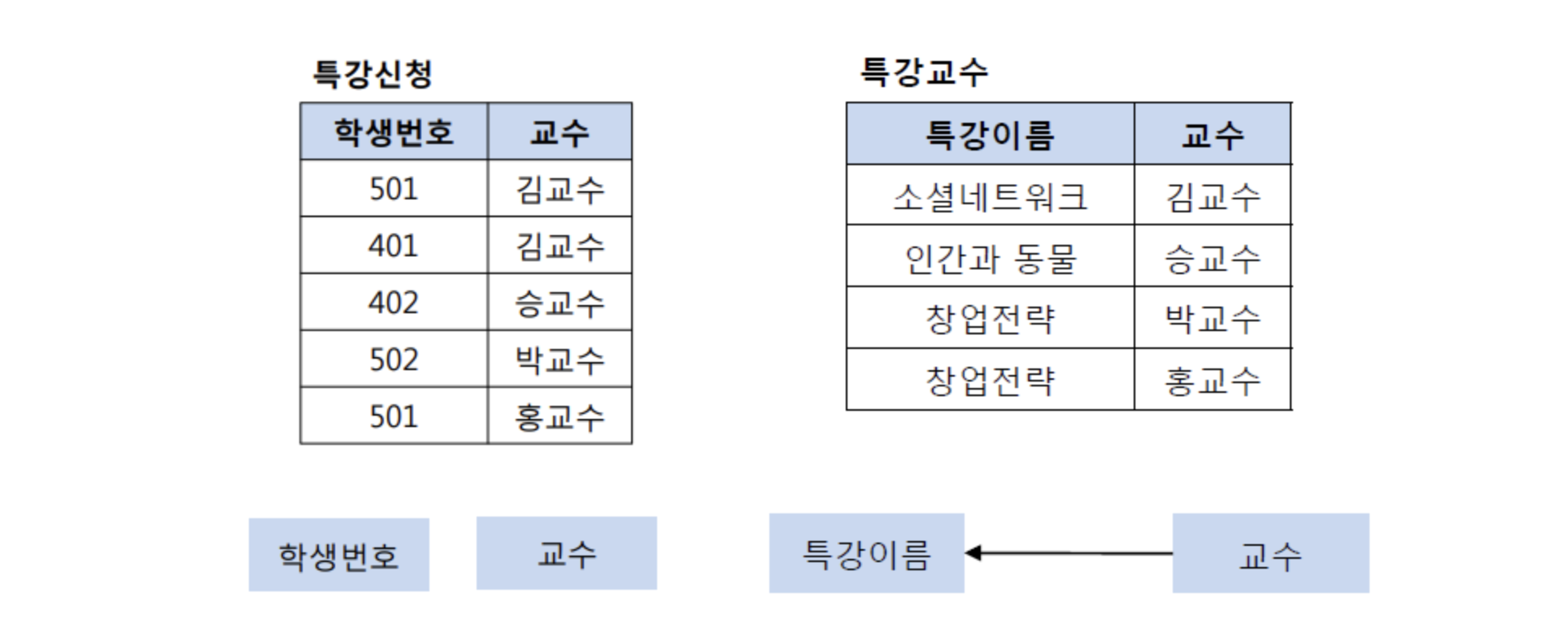
그런데 문제는 교수가 특강이름을 결정하는 결정자이지만, 후보키가 아니라는 점이다. 그렇기 때문에 BCNF를 위해 테이블을 분해해야하는데, 다음과 같이 특강신청 테이블과 특강교수 테이블로 분해할 수 있다.