How to overcome limitation of linear model
Linear models (선형 모델)
-
e.g.) logistic regression, linear regression
-
장점: efficient, reliable, closed form or convex optimization
-
단점: 모델 복잡도, 두 입력 변수간의 상호작용 이해 불가 (e.g. XOR 문제)
x의 비선형 함수를 나타내기 위해 선형 모델 확장
- 선형 모델을 𝒙가 아닌 변환된 입력 𝜙(𝒙)에 적용
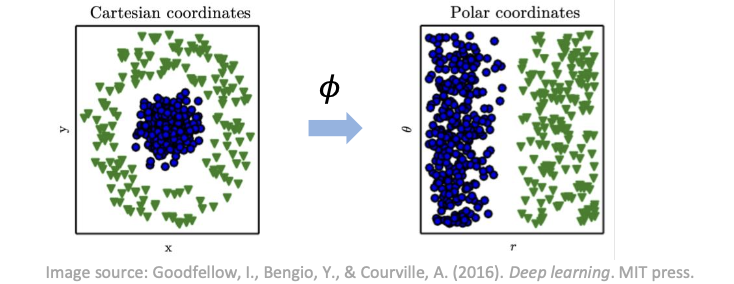
How to overcome limitation of linear model (cont.)
𝜙 를 어떻게 선정하는가?
-
매우 일반적인 𝜙 사용
-
e.g.) RBF 커널의 무한 차원
-
training set에 맞는 충분한 용량
-
test set에 대한 잘못된 일반화 (train에서는 잘 맞추지만 test에서는 잘 안됨)
-
-
수동으로 𝜙 엔지니어
-
e.g.) 전통적인 machine learning, feature engineering
-
도메인 전문성이 필요하지만 사람의 노력과 도메인 간 전송이 거의 필요하지 않다.
-
-
𝜙 학습
-
데이터로부터 학습
-
From a model y = f(x; Θ, w) = 𝜙 (x;Θ)Tw
-
Θ: to learn Θ from a broad class of functions
-
w: map from 𝜙(x) to the desired output
-
**Design decisions needed to deploy a feedforward network**
-
선형 모델과 동일한 설계 결정
-
optimizer / cost function / form of the input units and output units 결정
-
Gradient-based learning
-
-
고유한 feedforward network
-
hidden layer
-
activation functions
-
네트워크의 아키텍쳐
-
얼마나 많은 layer를 둘 것인가?
-
각 layer에 얼마나 많은 units을 둘 것인가?
-
어떻게 각각의 layer을 연결할 것인가?
-
-
-
학습
- back-propagation, modern generalizations
Training a Neural Network
-
비선형 신경망 → non-convex loss function (비볼록 손실함수) (선형모델과의 가장 큰 차이)
- 좋은 해를 찾기 어려워짐
-
신경망은 일반적으로 반복적인 gradient 기반 optimizer를 사용하여 훈련된다.
-
비볼록 손실 함수에 대한 확률적 경사하강법
-
수렴한다는 보장이 없다.
-
초기 파라미터에 예민하다
-
weights: 임의의 값으로 초기화
-
biases: 0 또는 양수 값
-
-
-
gradient를 계산하는것은 약간 더 복잡하다.
- backpropagation 에 의해 효율적이고 정확하게 수행된다.
Cost Functions
-
비용 함수는 종종 기본 비용 함수와 정규화 항을 결합한다.
-
대부분의 현대 신경망은 maximum likelihood의 원리를 사용한다.
- e.g.) 트레이닝 데이터와 모델의 예측 값 간의 cross-entropy
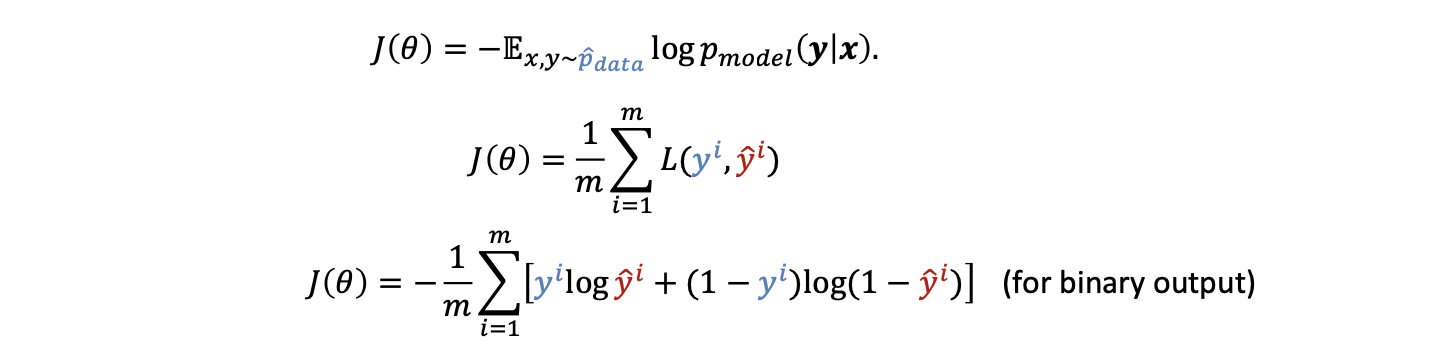
-
Mean squared error와 mean absolute error는 gradient 기반 optimizer와 함께 쓸 때 종종 안좋은 결과를 낸다.
- 포화되는 output units은 매우 작은 gradient를 생성한다. → 교차 엔트로피가 더 많이 사용된다.
Likelihood Function
-
우도 함수(likelihood)는 관찰된 데이터의 결합 확률을 선택한 통계 모델의 함수로 설명한다.
-
각각의 특정한 파라미터 Θ에 대해, 우도함수 p(x|Θ)는 관찰된 데이터 x에 대한 확률론적 예측이다.
-
주로 L(Θ|x) 라 쓴다.
-
e.g.) fair한 주사위 확률, unfair한 주사위 확률, p = (1/8, 1/8, 3/8, 1/8, 1/8, 1/8), X = (4,3,3)
-
주사위를 던졌을 때 4,3,3이 나올 확률
-
p(X|fair) < p(X|unfiar)
-
Maximum Likelihood Estimation
최대 우도 추정은 일부 관찰된 데이터가 주어졌을 때 가정된 확률 분포의 매개변수를 추정하는 방법이다.
-
𝜃 = argmax L(𝜃|𝑋)
-
likelihood를 최대화 시키는 parameter 𝜃
-
e.g.) fair dice and unfair dice p = (1/8, 1/8, 3/8, 1/8, 1/8, 1/8), X1 = (4,3,3), X2 = (5,2,5)
-
X1이 생성해낼 수 있는 최대 확률은 어떤 주사위 인가? unfiar dice
-
X2가 생성해낼 수 있는 최대 확률은 어떤 주사위 인가? fair dice
-
Linear regression → 최소 제곱
